一道奥林匹克试题条件的商榷



一道奥林匹克试题条件的商榷

江苏省泰州市姜堰区沈高镇夏朱村(225538)陈罗英江苏省姜堰中等专业学校(225500)陈宇

图1

在探求该题别证的过程中，笔者发现该题的条件“锐角⊿ABC”的“锐角”是否多余，有待商榷.

首先给出一个别证.

图2

∵I为内心，点E在⊿ABC的外接圆上，

又∵∠EIC=∠IBC+∠ICB=∠ACE+∠ICA=∠ECI，知⊿EIC为等腰三角形，EC=EI(4).

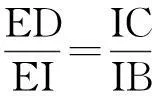
结果是，无论是参考答案，还是本文之证法均没有用到 “锐角⊿ABC” 的“锐角”这一题设条件.

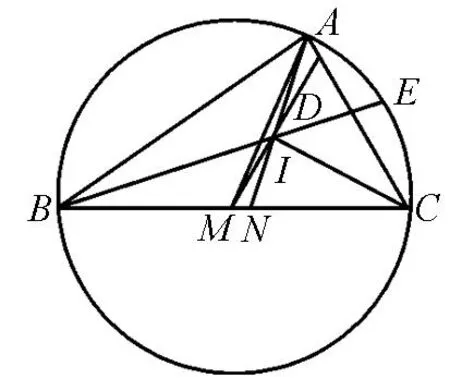
图3

可见，点N在线段MC上的两端点M，C之间.则⊿ABC的内心I在角平分线AN上的两端点A,N之间.因而内心I在⊿AMC内. MI与边AC的交点D在边AC上的两端点A,C之间.此时，点D在边AC上的位置与⊿ABC的形状无关.

同理，AB=AC，则MI与边AC的交点D与边AC上端点A重合(如图4).

AB

图4 图5

综上所述，MI与边AC的交点D在边AC上的位置只与∠BAC的两边AB,AC的大小相关，而与⊿ABC的形状无任何关联.

对于题设条件“锐角⊿ABC”的“锐角”值得商榷.

若不是命题者有意干扰解题者的审题及方法的

探求，则该条件多余.

数学一门是非常严谨的学科.这种严谨包括了其知识的真实，思维的缜密和教学的严肃，同时也必须在数学问题和解决上体现其严谨.当然在竞赛题中更不能出现有悖数学严谨的问题.笔者以为，该赛题中的条件“锐角”多余，应去除.

进而，该试题及两个变式可统一为：

该统一题的证明，除需按MI与直线AC的交点D在直线AC上的位置分类作图外(如图3,4,5)，证明过程可统一——亦如本文之别证或参考答案的证明过程.几乎一字不差(此略).有兴趣的读者不妨一试.

上述变式及统一，并非刻意而为.因为这种变式、统一及解题的普适性，能促进学生产生有效的联想，提升学生的思维能力和解题能力.

参考文献

[1]第11届中国东南地区数学奥林匹克,中等数学,2014,10(第26～30).