从一道高考题谈复习课的教学设计



从一道高考题谈复习课的教学设计

浙江省宁波市北仑区柴桥中学(315809)徐泽绕

1.问题提出

2015年高考浙江省理科数学第18题为：

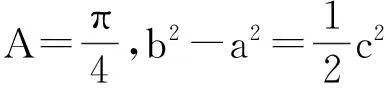
(1)求tanC的值;

(2)若ΔABC的面积为3，求b的值.

该题是一个常规的解三角形问题，应该是一个送分题，但根据笔者所在学校学生反映第一小题的解答并不顺利，甚至个别学生有一种无从下手的感觉.无独有偶，2011学年宁波市高一第二学期期末测试中的最后一道填空题，如下：

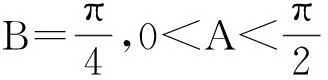
仔细对比一下两题，简直如出一辙，而且问2在这届学生高一的时候作为模拟试卷已经做过，为什么过了两年，经历高三的几轮复习还是会有问题呢？是不是我们的复习出现了问题？是不是我们太注重解题的技巧，太注重归纳题目的类型了呢？经过认真反思笔者认为，这应该是一种数学思想方法的缺失，数学思想方法指导解题的真谛还没有被我们的学生真正领会，导致的后果是，教师讲了无数遍，学生按图索骥，不断模仿，并没有真正理解和掌握这类题的本质.每次碰到都是一种新面孔，每次碰得跌跌撞撞，甚至答完题自己还云里雾里不知为何这么答.这种现象对我们高一阶段的复习和以后的学习都有很好的警示作用.恰逢高一刚好又是期末阶段，正余弦定理还是必考内容.因此为了让学生能站在理论的高度，在数学思想的指导下找到解题方法，笔者设计了一堂正余弦定理复习课.期盼同行斧正.

2.知识回顾确定目标

正余弦定理是解三角形的两大利器.其分别可以解决以下四类最基本问题：①已知两角和一边；②已知两边和其中一边的对角；③已知两边和其夹角；④已知三边.只要符合上述四类情况必能求解三角形，而且已知三角形涉及三个角和三条边六个量，在上述四种情况下显然已知三个量就可以求出另外三个量(已知三个角除外)，这种“知三求三”的解法就是解方程的思想，而且我们知道一个公式就是一个方程，有公式的地方必然有方程.带着方程的思想去解题，这就是本节课的第一个目标.那么在上述条件不满足，即已知条件不够的情况下呢？显然不能求值，不能求值的情况下往往是求最值或者范围，那么如何求范围呢？首先我们想到的是函数，因此在函数思想的指导下解题是这节课的第二个目标.

3.思想引领变式探究

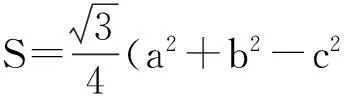
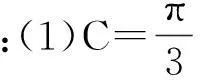
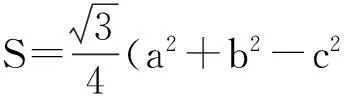
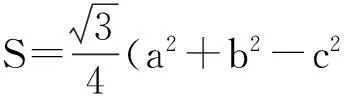
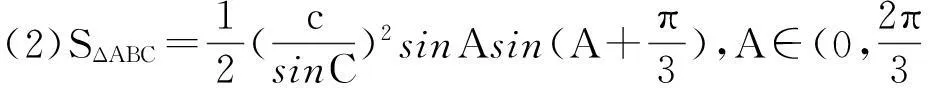
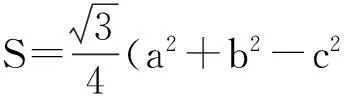
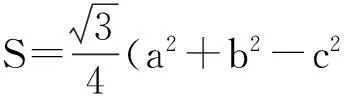
反思总结：通过上例和几种变式感受到题目中最大的特征就是只给了两个条件，即“一边一角”.不符合解三角形的四种基本类型.进而体会运用函数的思想求解三角形中的范围和最值问题，那么根据“一边一角”我们只得到一个方程，即c2=3=a2+b2-2abcosC=a2+b2-ab,若要解三角形还应补上什么样的条件呢？于是有：

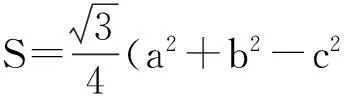
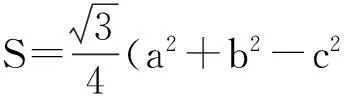
设计意图：加上一边a=2，在a2+b2-ab=3基础上已知a就很容易求得b，也就是转化为“两边及其一边对角”问题求解，当然也可去掉c这条边，补上a,b转化为上述四种类型中的“两边夹角”问题求解.除了再补成解三角形的四种基本类型即变式(5)，变式(6)以外，还可运用方程思想再列出关于a和b的另外一个式子，从而获解.这样又可得以下一系列变式题.

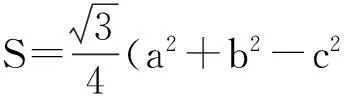
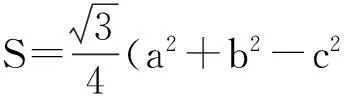
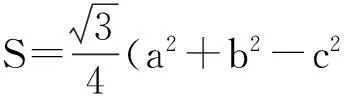
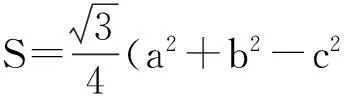
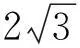
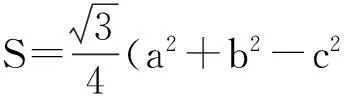
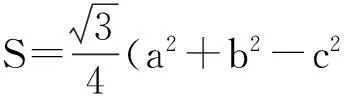
4.问题解决

通过以上的变式，再来看问1.

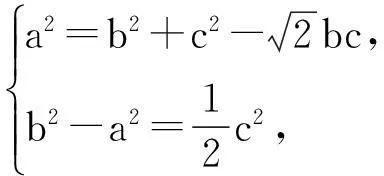
当三角形三条边中只涉及两个方程时虽然解不出方程，但是其中任何一边都可以表示另外两边，换言之由三条边的比例可以得到，同样也能求出三个角的三角函数值，但可以肯定任何一条边都不可能求得.

5.一点感言

实际教学中我们经常会碰到这样的现象，每到期中、期末复习，我们会发下很多针对性的练习，来应对兄弟学校的统测和地区性统测等，希望通过大量的训练题来提高学生的应试水平，从而取得好成绩.每当这时往往出现学生做题做得叫苦连天，老师练习讲得也厌倦疲乏，考完以后转入下一模块学习时，学生早已忘了不知学的什么东西现象.长此以往，教师身心疲惫，学生学而生厌，严重抑制了创新精神和后续学习的能力，这对师生都是一种“摧残”.笔者认为，题是做不完，也讲不完的，如何提高学生的学习能力和学习兴趣，应该让他们站在理论的高度来看待解题问题，而运用数学思想指导解题则是让学生掌握解题方法的理论武器，值得我们在平时的教学中去探索与加强.