一道质检试题命题思路的剖析



一道质检试题命题思路的剖析

福建省泉州第七中学(362000)吴宝树

函数与导数试题经常作为数学试卷的压轴题，学生对此类试题往往有畏惧的心理，得分率很低．这一类试题设计巧妙，新颖独特，思维量大，考察学生思维的抽象性、逻辑性，对学生的理解能力和自学能力都提出了很高的要求．实际上这一类试题很多来源于课本，学生如果能够洞悉试题的来源与构造过程，将会对问题的解决起到很大的帮助．本文以一道泉州市质检试题为例，剖析该试题的来源和命制思路，并将该试题拓展开来，分析这一类试题的解题思路，希望能对学生解决此类问题有一定的帮助．

1.试题再现

已知函数f(x)=lnx-ax在点A(1,f(1))处切线为l．

(Ⅰ)当切线l的斜率为2时，求实数a的值；

(Ⅱ)证明：无论a取何值，函数f(x)的图像恒在直线l的下方(点A除外)；

(Ⅲ)设点Q(x0,f(x0))，当x0>1时，直线QA的斜率恒小于2，试求实数a的取值范围．

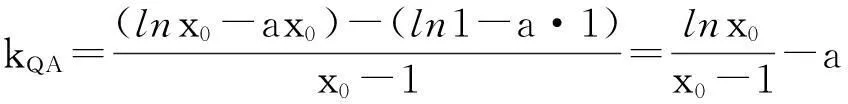
2.命题思路追踪

2.1课本寻源

本题难度适中，但这道试题的实测情况非常不理想．高三的学生在总复习过程中往往容易陷入题海战术，盲目大量的训练，而忽视了对教材的使用和学习．如果我们能够透过复杂的表面问题，看到命题者的命题意图，洞悉命题思路的变化，回归课本，就能化繁为简．本题中关键的一步是利用lnx≤x-1进行放缩，从而得到参数a的取值范围．而这一关键步骤其实来源于教材中的一道习题．

普通高中课程标准试验教科书数学选修2-2人教A版第32页习题1.3B组第一题：利用函数单调性，证明下列不等式，并通过函数图像直观验证：第(3)小题ex>x+1，x≠0．

2.2习题变式

由ex>x+1，x≠0两边同取对数得ln(x+1)

问题1已知函数f(x)=lnx+x，求f(x)在(1,0)处的切线方程．

问题2求函数f(x)=lnx-(x+1)的最大值．

2.3引入参数

含参问题涉及知识广泛，综合性强，方法灵活．将题目变式为含参问题后，无疑增加了题目的难度，学生对含参问题的掌握情况能够很好地反映出学生的数学学习水平．

问题3已知函数f(x)=lnx+ax在(1,0)处的切线方程为y=2x-1，求参数a的值．

问题4已知函数f(x)=blnx+ax在(1,0)处的切线方程为y=2x-1，求参数a，b的值．

2.4数形结合

数形结合将“数”与“形”结合起来，使数学问题由易到难，化繁为简，使数学问题更加直观，给学生的解题增加了挑战．基于此，可以利用函数图像与其切线的位置关系，编拟如下两个试题．

问题5证明函数f(x)=lnx+x的图像恒在其切线y=2x-1的图像下方．

问题6已知函数f(x)=lnx+ax在(1,f(1))处切线为l，且函数f(x)=lnx+ax的图像恒在其切线l的图像的下方(切点除外)，求实数a的取值范围．

2.5引入动点

将切点位置固定，另一个点在曲线上运动起来，整个题目充满活力，也增加了解题的难度．

问题7已知函数f(x)=lnx+x，点P(1,f(1))，Q(x0,f(x0))(x0>1)，证明：割线PQ的斜率恒小于2．

问题8已知函数f(x)=lnx+ax，点P(1,f(1))，Q(x0,f(x0))(x0>1)，若割线PQ的斜率恒小于2，求参数a的取值范围．

3.成题拓展

以上八个小问题从不同的角度对课后例题进行了变式拓展，组合在一起就是本文开始的引例了．每个问题步步推进，一步一步的靠近命题者的思路．学生如能掌握这一命题思路，无疑将对问题的解决起到很大的帮助．

我们可以在此基础上对本题进行变式拓展．由于指数函数和对数函数互为反函数，其图像关于直线y=x对称，因此我们可以将以上变式步骤应用于指数函数，得到如下题目：

已知函数f(x)=ex+ax在点P(0,f(0))处切线为l．

(Ⅰ)当切线l的斜率为2时，求实数a的值；

(Ⅱ)证明：无论a取何值，函数f(x)的图像恒在直线l的上方(点O除外)；

(Ⅲ)设点Q(x0,f(x0))，当x0>0时，直线PQ的斜率恒大于2，试求实数a的取值范围．

4.点击高考

高考试题中也有大量是以此思路为背景命制的，在此以湖北和辽宁高考题为例，加深学生对该类试题的理解．

例1(湖北高考题)(Ⅰ)已知函数f(x)=lnx-x+1,x∈(0,+∞)，求函数f(x)的最大值；

(Ⅰ)求a，b的值；

解析：(Ⅰ)易得a=0，b=-1；