一脉相承的两道高考压轴题



一脉相承的两道高考压轴题

福建省龙岩第一中学(364000)胡寅年

由抛物线焦点弦生成的射影定理三角形引申出来的问题，是抛物线几何性质中极为重要的内容，同时也是高考命制试题的源泉之一.对它们的深入探究，可极大地丰富我们对抛物线几何性质内涵的认知.

图1

性质1如图1，设抛物线y2=2px(p>0)的焦点为F，经过点F的直线l交抛物线于P、Q两点，P、Q在准线上的射影分别为P1、Q1，则ΔP1FQ1是一个射影定理三角形．

性质2如图2，设抛物线y2=2px(p>0)的焦点为F，经过点F的直线l交抛物线于P、Q两点．以P、Q 为切点分别作抛物线的切线，则这两切线的交点R在抛物线的准线上，且ΔPRQ是一个射影定理三角形，(SΔPQR)min=p2．

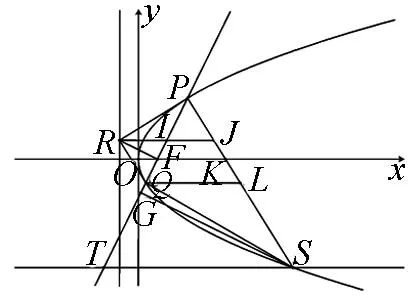
图2

证明：设P(x1,y1)、Q(x2,y2)，经过点P(x1,y1)的切线方程是y-y1=k(x-x1)，则

容易看出，下面的题1就源自抛物线(焦点弦)的上述几何性质. 事实上，将性质2中的抛物线y2=2px(p>0)绕原点O逆时针旋转90°，再取p=2的情形，并进行适当的包装，即为试题1．

(Ⅱ)设ΔABM的面积为S，写出S=f(λ)的表达式，并求S的最小值.

题2(2014年山东卷压轴题)已知抛物线C:y2=2px(p>0)的焦点为F，A为C上异于原点的任意一点，过点A的直线l交C于另一点B，交x轴的正半轴于点D，且有|FA|=|FD|.当点A的横坐标为3时，ΔADF为正三角形.

(Ⅰ)求C的方程；

(Ⅱ)若直线l1∥l，且l1和C有且只有一个公共点E， (ⅰ)证明直线AE过定点，并求出定点坐标；(ⅱ)ΔABE的面积是否存在最小值？若存在，请求出最小值；若不存在，请说明理由.

题2与题1一脉相承，难度却比题1大得多，其一：第(Ⅱ)问的第(ⅰ)小题，本质上是题1第(Ⅰ)小题的一个变式，证明方法貌似差不多，可实际情况不是这样的；其二：第(Ⅱ)问的第(ⅱ)小题，若发现不了ΔPQS面积与ΔPQR面积之间的倍数关系，而是直接去求ΔPQS的面积，计算量将会非常之大. 题2的引申结果如下：

性质3设抛物线Γ:y2=2px(p>0)的焦点为F，P为Γ上异于原点的任意一点，过点P的直线l交Γ于另一点S，交x轴正半轴于点K，且有|FP|=|FK|．若直线l1∥l，且l1和Γ有且只有一个公共点Q．证明：P、F、Q共线，且(SΔPQS)min=4p2．