把握选考内容，提升复习效益*



把握选考内容，提升复习效益*

河南省濮阳市第一高级中学(457000)关传平梁文强

近几年来，高考改革在不断的进行，数学的变化也比较明显，纵观其变化，新课标全国卷Ⅰ在全国高考中仍占有重要位置，甚至起着引领的作用．广东、湖北、陕西、四川、重庆、福建、安徽等省份也将于2016年使用新课标全国卷Ⅰ，这使得新课标全国卷Ⅰ的重要性更加突出，然而新课标全国卷Ⅰ与各省市高考卷在选考内容上有明显差异．笔者所在的省份从2011年至今一直在使用新课标全国卷Ⅰ，所以对新课标全国卷Ⅰ有深刻体会，结合新课标全国卷Ⅰ与各省市高考卷的考试情况，本文将在新课标全国卷Ⅰ选考内容教学上做一些分析和探讨，以期对进入2016年使用新课标全国卷Ⅰ的考生和即将使用新课标全国卷Ⅰ的莘莘学子，以及奋斗在高三一线的数学教师有些许帮助．

一、选考内容命题规律

研究近五年来的新课标全国卷Ⅰ发现：选考内容文理科一样，且都有三个小题．试题来源于教材，但又高于教材；题目难度适中，但稳中有变；考查的知识点明确，但问题的解答灵活多样，突出对能力的考查；符合《课程标准》和《考试说明》对选讲内容的教学要求，落实了选考内容，使不同层次学生的能力得以发挥．

1.平面几何选讲

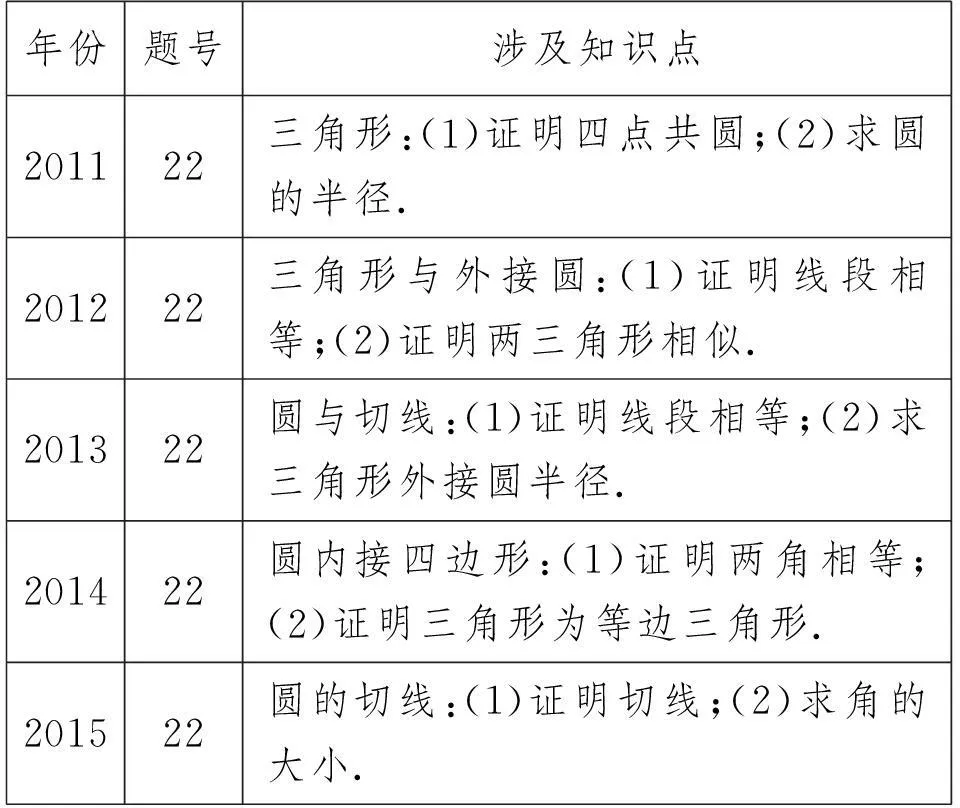
年份题号涉及知识点201122三角形:(1)证明四点共圆;(2)求圆的半径.201222三角形与外接圆:(1)证明线段相等;(2)证明两三角形相似.201322圆与切线:(1)证明线段相等;(2)求三角形外接圆半径.201422圆内接四边形:(1)证明两角相等;(2)证明三角形为等边三角形.201522圆的切线:(1)证明切线;(2)求角的大小.

平面几何通常的考查方式是一证一算．此类题的运算量较小，但有一定的思维深度，重在考查学生的逻辑思维能力和推理论证能力．试题一般以考查基本定理为主线，解答此类题有时需要添加辅助线，使数和形有机结合起来．

2.极坐标与参数方程

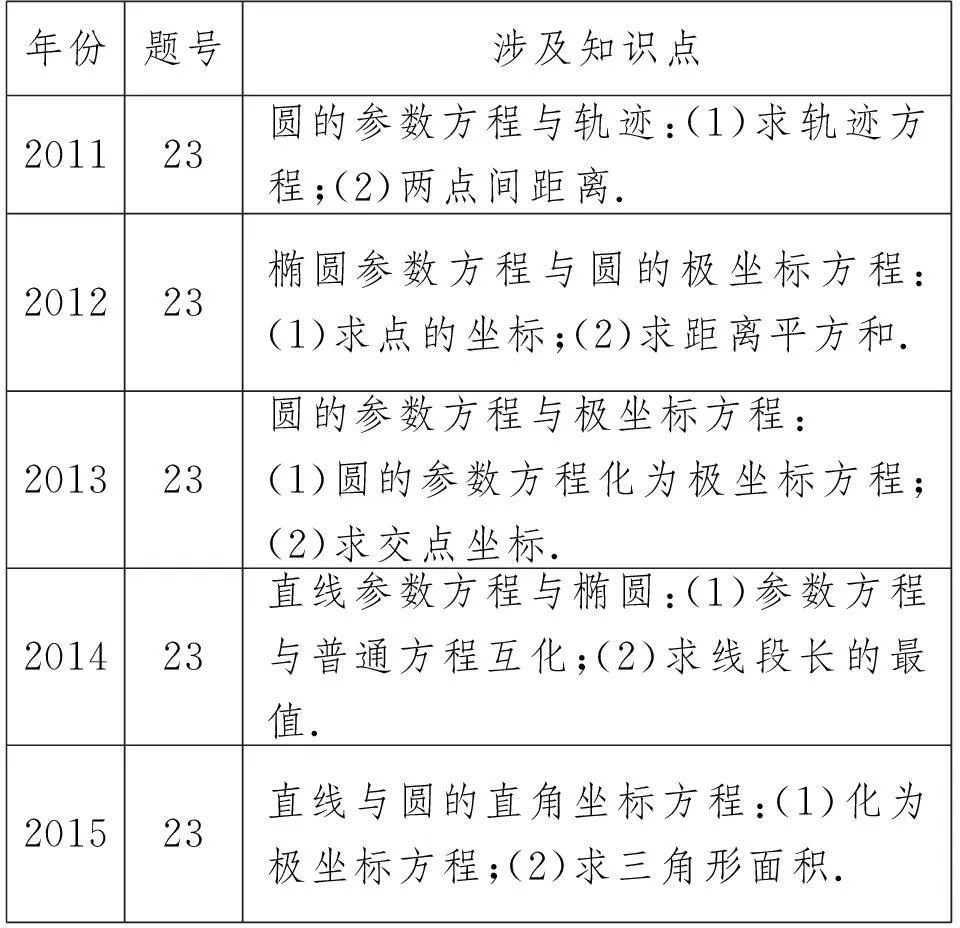
年份题号涉及知识点201123圆的参数方程与轨迹:(1)求轨迹方程;(2)两点间距离.201223椭圆参数方程与圆的极坐标方程:(1)求点的坐标;(2)求距离平方和.201323圆的参数方程与极坐标方程:(1)圆的参数方程化为极坐标方程;(2)求交点坐标.201423直线参数方程与椭圆:(1)参数方程与普通方程互化;(2)求线段长的最值.201523直线与圆的直角坐标方程:(1)化为极坐标方程;(2)求三角形面积.

坐标系与参数方程，这部分内容主要以必修2和选修2-1教材中解析几何部分为载体，思维难度相对比较低．解答时一般情况下联立方程即可，但计算时需要注意准确性.对于此类问题，学生只要掌握了普通方程和参数方程以及极坐标方程三者的互化、参数的意义，联系前面已经掌握的直线与圆的位置关系，以及直线与椭圆的位置关系，就能灵活解决．

3.不等式选讲

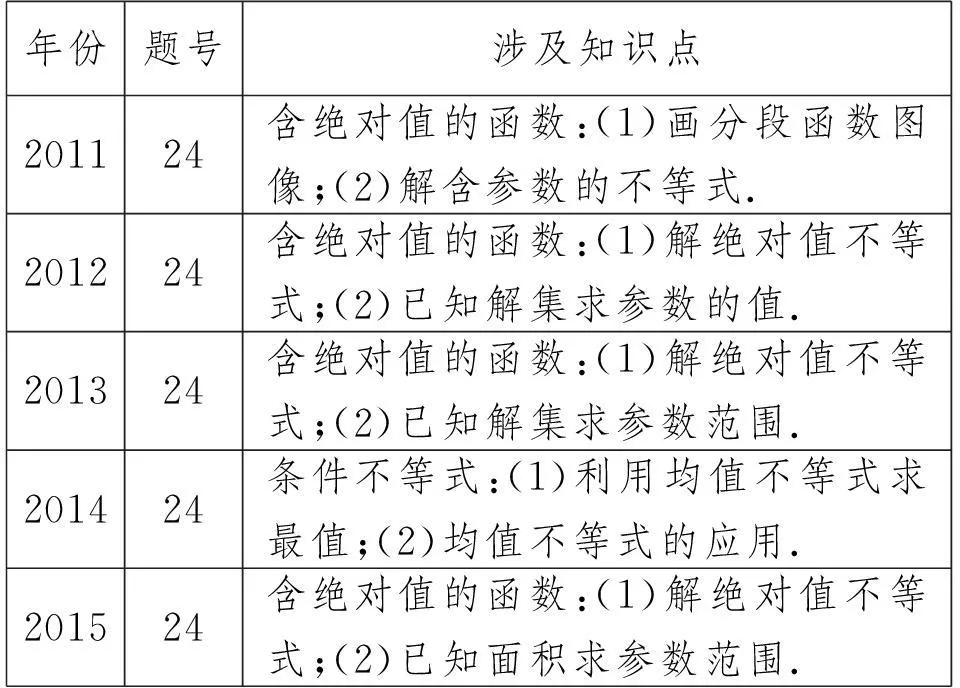
年份题号涉及知识点201124含绝对值的函数:(1)画分段函数图像;(2)解含参数的不等式.201224含绝对值的函数:(1)解绝对值不等式;(2)已知解集求参数的值.201324含绝对值的函数:(1)解绝对值不等式;(2)已知解集求参数范围.201424条件不等式:(1)利用均值不等式求最值;(2)均值不等式的应用.201524含绝对值的函数:(1)解绝对值不等式;(2)已知面积求参数范围.

不等式选讲在主要考查绝对值的几何意义、含绝对值不等式的求解的同时考查学生分类讨论和数形结合的数学思想．有时问题也会涉及不等式的基本性质和重要不等式的应用等．不等式的证明在必修5模块是重点讲解内容，学生在熟练掌握基本公式和证明方法的前提下，答题轻而易举．

二、选考内容考试情况

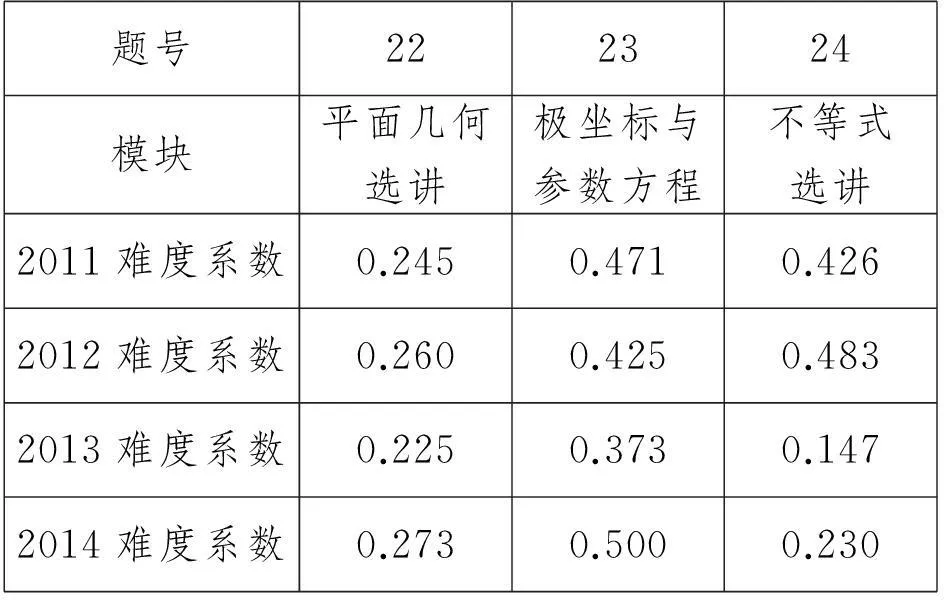
题号222324模块平面几何选讲极坐标与参数方程不等式选讲2011难度系数0.2450.4710.4262012难度系数0.2600.4250.4832013难度系数0.2250.3730.1472014难度系数0.2730.5000.230

从上表中我们可以发现，从近几年的选考试题看，得分率极低．即便是做相对容易的极坐标与参数方程选讲题，平均分也没有突破5分；选考试题中，平面几何选讲相对比较稳定，但试题总体偏难，不易得分；不等式选讲难易不定．选考题实际上相当于大纲版的第17题，属于容易题，事实上，考试中却成为学生的失分题，这不得不引起一线老师的反思与重视．从考生反馈的情况来看，选考平面几何的学生主要辅助线不会做导致无从下手而失分；选考不等式的学生，主要是解题不规范、计算失误、分类讨论模糊导致失分；选考极坐标与参数方程的学生主要是三种曲线方程形式的选择不恰当导致出错失分．选考试题像水中月，镜中花，我们能看到清，却总是拿不到满分，这种现象应引起我们一线教师的重视，在平时的教学中要尤其注意，力争避免此类现象在考试中出现．

三、选考内容教学误区

1.三个模块开设不全

有些学校为减轻学生负担，节约高三复习时间，直接抛弃两个模块，只讲一个模块，其它模块学生自学，教师总担心遍地开花会加重学生的负担，希望学生一枝独秀，精练一类选考题就能包打天下．事实上，考试时学生知识面狭窄，知识单一，对于试题没有选择余地，难易也只能碰运气，不会的只能不得分．平时我们少开一本选考内容，考试中学生就少一种选择，多开一本选修，就多一次得高分的机会，况且知识之间是相互联系的，同一学科内的几个模块之间有千丝万缕的联系，选考内容的延伸和拓展，对于做必考题也大有帮助．在必考题里面出现了选考部分的内容，对于学过的学生来说是已经熟悉的内容，而对于没有学过的学生来说就是新材料、新信息，得分差别更大．

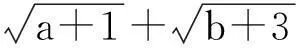
评注:利用不等式选讲内容中重要的柯西不等式，方法简单、快捷．

例2(2015江苏卷理科第12题)在平面直角坐标系xOy中，P为双曲线x2-y2=1右支上一个动点，若点P到直线x-y+1=0的距离大于c恒成立，则实数c的最大值为.

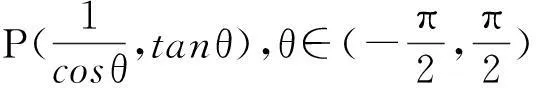
评注:利用双曲线参数方程求最值，通俗易懂，简单明了．

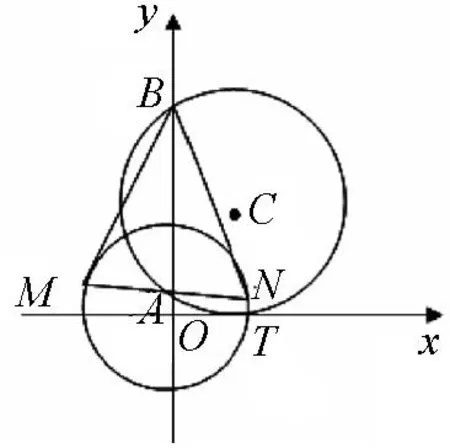
图1

例3(2015年湖北卷理科第14题)如图1，圆C与x轴相切于点T(1,0)，与y轴正半轴交于两点B，A(B在A的上方)，且|AB|=2.

(1)圆C的标准方程为；

(2)过点A任作一条直线与⊙O:x2+y2=1相交于M，N两点，下列三个结论：

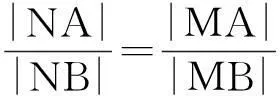
其中正确的结论的序号为(写出所有正确的结论的序号)

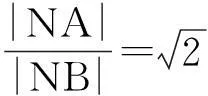
评注:把平面几何知识迁移到解析几何中，减少了运算量，降低了试题的难度．

上述三道题足以显示平面几何，不等式选讲以及极坐标与参数方程选考内容的重要性，其它非选考试题也可以用选考内容的知识作答，且方法简单，计算量小，能为考生在考场上赢得更多的答题时间．故所有选考内容都有开设的必要，我们要坚信知识面越宽，解题自由度越大，灵活度越高，得分也会越高．

2.选考模块讲解太快

很多学校为了赶课，挤压必修课与选修课时间，大部分学校在高二下学期五月底结束所有必修课与选修课，然后用一个月左右的时间完成不等式选讲、平面几何选讲、极坐标与参数方程选讲三本书的讲授，基本上十天一本书，草草结束选考内容，由于没有与之匹配的消化时间和习题巩固时间，学生是囫囵吞枣，一知半解，仅仅停留在知识的表层上，对知识的理解不到位，掌握不到位．到了高三一轮复习结束时再次复习选考内容，相当于热夹生饭，学习效果可想而知．

图2

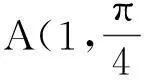
从上述两种解题方法中我们可以发现学生的解法仍然处在原始的解法中，不会利用新知识解题，而是转了弯才得到结果，究其原因是课堂上知识的掌握不到位，知识还不能自由迁移．这在某种程度上也是新课讲授过快，学生消化不良造成的．

3.试卷讲评成摆设

很多教师讲评试卷也不管学生选考内容答题情况，不评讲选考内容．一方面，是因为教师对某些选修模块不熟悉，所以课堂上是一句话带过，或者根本不讲；另一方面，教师从思想上认为简单，再加上学生做题情况不一样，学生只听他选做的那道试题，其它没做的就不听讲，所以老师不愿意讲评．久而久之，选考内容被放在遗忘的角落，学生只能自己看答案．

(1)求直线l的极坐标方程；

(2)若直线l与曲线C相交于A，B两点，求|AB|．

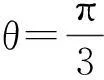
4.学生掌握内容单一

一般情况下，学生如果习惯于做三道题中的某道题，他们每次就选做该试题，这种偏好导致了学生放弃其它选考内容，久而久之，对其它选考内容越来越陌生，考试时一旦经常选考的题目难度增加，就手忙脚乱，思维混乱，不知所措．知识单一不但不利于学生成绩的提高，还为今后进一步学习埋下了隐患．

(2)过坐标原点O作C1的垂线，垂足为A，P为OA的中点，当α变化时，求P点轨迹的参数方程，并指出它是什么曲线．

这道题的第2问在当年的高考中难倒不少考生，如果考生平常只喜欢做极坐标与参数方程这个模块，那么高考中至少会失掉5分．

例7(2014年新课标全国卷Ⅰ第24题)

(1)求a3+b3的最小值；

(2)是否存在a，b，使得2a+3b=6？并说明理由．

当年很多考生看到这道题就懵了，平常都是考含绝对值不等式，这次却换了频道，学生很不适应，再加上遇到三次方，学生更是无从着手．若考生平常习惯于做不等式，再去做其它题，心里没底，思来想去，浪费了很多宝贵的时间，也失去了很多分数．

四、选考内容备考建议

1.开设齐全，自主选择

三个选考模块全部开设.首先，学生说不定对哪一模块感兴趣，理解更快，掌握更熟练，多开一个模块多一些选择．其次，若其它学校开设，自己的学校不开设，没参加考试在知识上就已经输了，还何谈高考成绩．故选考内容要全部开设．一方面，给学生在考试时留下了选择的余地；另一方面，扩大了学生的知识面，使学生可以触类旁通，优化解题方法，而且对选考内容之外的试题有一定的帮助，各个模块在解题时各有千秋，不等式内容贯穿于整个高中，极坐标与参数方程对求函数最值，以及圆锥曲线问题起到很大帮助，平面几何的学习为立体几何奠定了基础．近几年的教学实践证明，选考内容都开设效果更好．最后，新课标的基本理念之一是提供多样课程，适应个性选择，高中数学课程应为学生提供选择和发展的空间，为学生提供多层次，多种类的选择，学生可以在教师的指导下进行自主选择，必要时还可以进行适当的转换、调整．

2.钻研考纲，把握难度

随着更多的省份加入新课标全国卷Ⅰ，应关注新课标全国卷Ⅰ与各省市的高考题在命题上的差异，特别是选考内容的差异．近几年来，像福建卷考矩阵与变换，这是全国卷不考的内容；广东卷以填空题的形式考查选考内容，而新课标全国卷Ⅰ以解答题的形式考查；安徽卷理科只考极坐标与参数方程，而文科不考选考内容；四川卷文理都不考选考内容，湖北卷不考不等式选讲等.从中我们可以看出选考内容考查的内容不同，难易程度也不一样．所以一线教师应认真钻研新课标全国卷Ⅰ的考试大纲，掌握命题方向和重难点．

3.认真评讲，提高效率

教师在试卷讲评时，应根据学生的答题情况，统计学生错误原因，有针对性讲评，教师的重视方能引起学生的重视，教师的课上讲评在一定程度上可以让学生发现错误并及时改正自己的错误．学生课下对答案的效果远远不如老师细致的点拨，此外，教师也可以规定考试答一道题，考完后再把其余两道题以考试的标准做一做，即在教师的督促下完成三道选考题，从而有的放矢的加强对三道选考题的训练，确保考试时稳拿满分．

4.合理指导，有效解答

一般情况下，学生按试题顺序解答试题，但学生往往会在第20题圆锥曲线和第21题导数题耗费大量时间，待做选考题时，可能到了最后15分钟提示，学生更是手忙脚乱，没有心思做下去，所以教师对学生答题顺序的合理指导尤为重要，告诉学生一般情况下，完成第17题，第18题后就该转移到选考题上．学生与其在第20，21题上花费时间也不会，不如解答时先做选考内容，再按正常顺序做，正像有人说的：考试成功就是把自己会做的题做对，我们正是改变了顺序，做对了自己会做的题，这就叫成功．

5.夯实基础，融会贯通

选考题中，平面几何主要考查相似三角形，平行线截线段成比例定理，直角三角形射影定理，圆的基本性质，圆幂定理，圆周角定理，切线等；极坐标与参数方程主要考查参数方程的互化，直线、圆与椭圆的参数方程，参数的几何意义等；不等式选讲主要考查含绝对值不等式的解法和不等式的证明方法等．

总之，三道题目在能力考查上各有千秋，思维能力强的学生可以选择平面几何试题，在平时训练中应加强分析和推理能力的培养；运算能力强，且熟悉解析几何的学生可以选择极坐标和参数方程试题，平时训练应注意运算的准确性；公式熟练，代数式处理能力较强的学生可以选择不等式试题，平时应加强转化能力的培养．当然，不管选考那类题目，都必须有扎实的基础知识，缜密的逻辑思维推理能力，以及良好运算求解能力.只有这样，才能居高临下，运筹帷幄，决胜千里．

参考文献

[1]梁文强，曲凡连．分析试卷，把握方向，备考2016[J]．中学数学研究(上半月)，2015．9．

[2]曾辛金．近六年全国高考数学课标卷试题分析与备考建议[J]．中学数学研究(上半月)，2015．9．

[3]兰竹．运筹帷幄方能决胜千里[J]．数学教学通讯(中等教育)，2015．9．

[4]教育部考试中心．高考理科试题分析(2012年版)[M]．高等教育出版社，2013．1．

[5]教育部考试中心．高考理科试题分析(2013年版)[M]．高等教育出版社，2014．1．

[6]教育部考试中心．高考理科试题分析(2014年版)[M]．高等教育出版社，2015．1．

本文为2015年度河南省基础教育教学研究项目“新课改理念下高三数学高效复习策略研究”(课题批准号：JCJYC150309115)的研究成果．