面积法与极限思想的形成*



面积法与极限思想的形成*

江西师大教育学院(330022)

胡细细江西师大数信学院(330022)刘咏梅

1.引言

高中数学有关极限的教学问题引起了广泛的讨论和研究，极限思想是基本数学思想之一，在教学中，极限的符号广泛使用，没有极限的语言会使教学显得很不自然．[1]而从现行的高中数学教材来看，对于极限我们主要是利用“趋于”、“逼近”、“无限接近”等进行直观描述，并没有给出严谨的“ε-δ定义”．学生在学习导数和微积分的时候往往会产生一种模糊的认识，对于涉及极限思想的问题也不能很好的解决．从数学的发展历程来看，对曲面面积的探索正是极限思想形成的重要基础．如圆的面积问题一直是古代数学家孜孜不倦探索的数学问题，公元3世纪，中国伟大数学家刘徽采用割圆术求圆面积；公元12世纪，印度人用“印度圆”求圆面积的方法，到后来开普勒(Kepler，J．)用无限个微小三角形求圆面积的方法．[2]借助面积关系解决问题的面积法不仅仅是一种古老的方法，也是个年轻的方法[3]，张景中先生通过“面积法”，为几何开启了新的纪元．它为学生直接观察问题提供了很好的素材，给学生思考问题提供了支点．在教学中能否利用面积法，提升学生对极限的认识，促进极限思想形成，从而更有效的运用极限思想解决问题，是一个值得探索的问题．

2.面积法对极限思想的意义

面积法是利用研究对象“形”的关系进行思维的方法，是利用思维对象变化过程中面积不变性将问题进行转化的，是辩证思维在数学问题解决中的运用．任何几何图形，其面积是确定的，面积法是根据几何量与涉及的有关图形面积之间的内在联系，将问题转化为面积的相关问题，从而把要论证的几何量之间的关系转化为有关面积之间的关系，并通过图形面积的等积变换对所论问题进行求解的方法．[4]面积法是形成数形转化、有限无限转化、化曲为直等重要思想的基础之一，这些思想为极限的形成奠定了基础，因而，将极限问题转化为面积问题，回归问题本源，是解决问题的重要途径，也是学生形成极限思想的重要途径．

2.1建立“形”与“数”的联系

数学是研究空间形式和数量关系的科学，“形”和“数”是构成数学的重要内容．毕达哥拉斯学派很早就提出了有关“形数”的研究，并强烈地提出将数看作几何思维元素．古希腊亚历山大时期，运用几何的知识处理等价的代数问题，如用线段代替数、两数乘积的意义看成两边长等于两数的矩形面积等．很多时候代数问题的解决往往需要借助面积，如用面积的关系来处理不等式问题．极限思想的运用之一，也是借助极限经历形与数的相互转化，借助面积关系，进行面积分解和求和，这有助于帮助学生体会数形转换的过程，有利于极限思想的形成．其联系可表示为以下关系.

2.2建立“无穷”与“有穷”的联系

Hilbert指出“数学是处理无穷的科学”[5]，数学中无穷的研究往往转化为有穷的问题进行思考．面积法是由“有穷”向“无穷”过渡的重要方法，利用面积法对“有穷”的直观认识，有利于人们接受“无限”思维，这也是创造极限和微积分的重要依据．

从度量最简单的矩形面积，到曲边形面积，经历了漫长的发展过程，在割补变换中，思维也逐渐由“有穷”向“无穷”慢慢发展．由于面积守恒，面积的大小始终是“有限”的，图形结构的“割补移动”不会引起面积的改变，但是可以将图形“无限”的分割，如分割成若干个正方形、矩形、三角形等图形，因此面积也是“有穷”和“无穷”结合的有效载体．在利用面积关系进行割补转化的过程中，人们对有穷和无穷的认识也随之不断加深，逐渐萌芽了极限的思想，奠定了微积分的基础．

2.3建立“直”与“曲”的联系

古希腊三大著名几何问题之一有化圆为方，这一问题的探索，是提出由直到曲解决问题的重要依据．如从等腰直角三角形—正方形—圆—椭圆(如下图)的面积的思考，经历了特殊到一般的过程．可以得到一般的圆和椭圆的面积为s=kab形式，其中a为“中位线段长”，b为“高”，进而提出曲边梯形等面积的猜想，这正是微积分计算原理的基本思想之一.基于这一基本思想，极限思维在历史的道路上也前进了一大步．

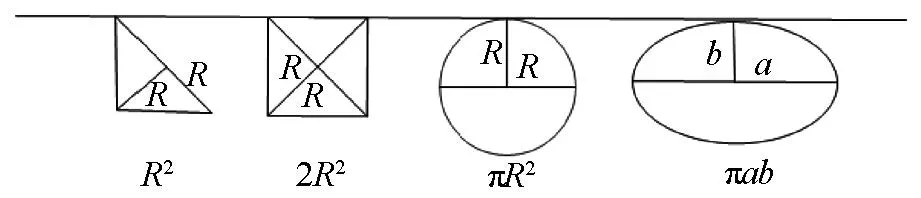
通过无限逼近，借助已有的面积计算，推广到一般的封闭的曲边图形面积，这是极限思想的重要体现，不仅孕育出了微积分，其本身也是解决问题的重要方法．有了微积分这一重要思想和工具，可以讲很多问题可以转化为面积之间关系，通过微积分得以解决．

2.4解决极限类函数不等式问题

面积法的具体运用是将需要研究的问题转化为面积问题，借助面积之间关系来解决．极限类函数不等式问题也是高中数学重要的一类问题，面积法是解决这类问题的一种有效方法．这一方法是通过建立函数关系，将问题转化为面积之间的关系，再将面积问题借助微积分来解决，达到解决原问题的目的．

例(2012年天津高考题)已知函数f(x)=x-ln(x+a)的最小值为0，其中a>0．

(Ⅰ)求a的值；

(Ⅱ)若对任意的x∈[0,+∞),有f(x)≤kx2成立，求实数k的最小值；

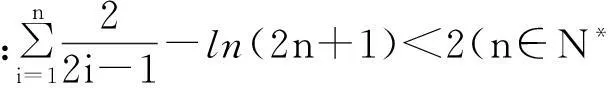
析解：(Ⅰ)(Ⅱ)略，下面讨论(Ⅲ)．

步骤一：将原问题借助函数转化为面积问题．

根据题目中的条件构造函数关系式，正确绘制相应的图形，并使图形能够较为直观地反映相应的数量之间的关系，揭示出数与式的内在属性．在此过程中直观思维是解决问题的基础，是由形的问题向数的问题转化的前提．

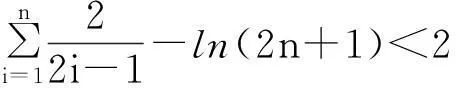
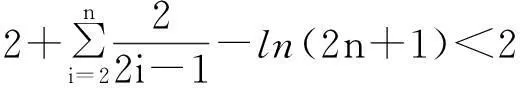
步骤二：建立面积之间的关系．

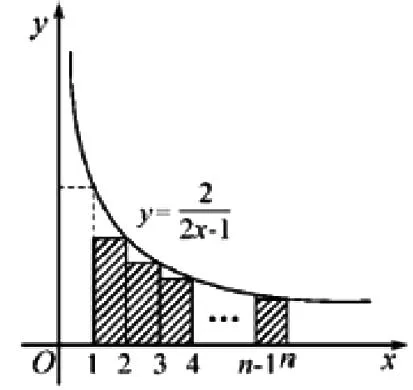
借助所作的图形仔细观察，探究图形内在的本质属性所蕴含的数量关系，并进行较为合理、准确的猜测，衍生出新的数与式．

由函数图形(如右)可知矩形面积和曲边梯形面积的关系，在区间[1,n]上的n-1个小矩形的面积之和小于曲边梯形的面积．

步骤三：面积关系转化为代数关系进行判断．

以上通过图形与构造代数式及将其进行转换，从而实现了数——形的相互转化，形成了相应的转化思维，并通过必要的计算，从而判断其较为复杂的数量关系．

解决上述问题的基本思路是将需要解决的问题转化为函数问题，将函数问题转化为面积关系问题，将面积关系问题转化为积分问题．这也是借助面积法解决函数不等式的基本思路．

3.结语

华罗庚说过: “数缺形时少直观，形少数时难入微”，数可以结合形进行直观的解释，在数—形的转化的过程中，思维也在不断的发展．面积问题的研究是极限思想的重要基础，基于极限的微积分又为解决数学问题提供重要的思路．

当然，在解决问题的过程中可综合运用到函数、不等式、定积分、面积等数学知识，运用数形结合、函数、化归、割补等重要思想方法．并由数的特点通过类比、联想、创造等思维活动，构造出相应的面积，并经历观察、猜想、顿悟，由特殊到一般的思维探究过程，从而逐渐形成正确的极限思想．

参考文献

[1]俞求是．高中新课标函数与微积分有关内容的处理研究[J]．课程·教材·教法，2010，30(9)：59-62.

[2]《数学辞海》编辑委员会编.数学辞海·第一卷[M].北京：中国科学技术出版社.2002.

[3]张景中．面积关系帮你解题[M] ．合肥：中国科学技术大学出版社，2013．1.

[4]张奠宙，宋乃庆．中学几何研究[M]．北京：高等教育出版社，2006．

[5]匡继昌．微积分和无穷小量的哲学思考[J].数学教育学报,2007,02:1-3.

[6]王新宏．赏析高考定积分试题[J]．中学数学杂志,2015,03:58-60.

江西省学位与研究生教育教学改革项目支助，课题编号JXYJG-2012-028；江西省高等学校教学改革课题，课题编号：JXJG-14-2-25.