打开二面角,翻开立几新篇章
2016-05-05张义斌
打开二面角,翻开立几新篇章
浙江省宁波市镇海中学(315200)张义斌
立体几何是高中阶段考查空间想象能力的主要载体,因此近些年来,它一直是各地高考热点.立体几何在人教版中的内容安排先是“立体几何初步”,再是“空间向量与立体几何”,呈螺旋式上升,适应学生的认知能力.然而求二面角是很多学生始终难以逾越的鸿沟,如何帮助学生清除这只“拦路虎”,如何培养学生的空间想象能力,如何提高学生分析问题的能力,这是我们一线教师亟待解决的一个重要课题.
虽然随着后期空间向量的引入,学生欣喜地找到了一种用代数研究空间几何的方法,巧妙地避开了寻找二面角这个难点,但是这也导致了很多学生只会用“空间向量”这一只脚走路,将空间想象能力的练习丢在一边的尴尬局面.各地高考命题的专家也敏锐地发现了这一令人堪忧的现象,因此近些年的立体几何大题逐渐呈现出难以建系的趋势,这就要求一线教师始终应当要求学生用“两条腿”走路.接下来笔者谈谈自己对二面角这块内容粗浅的教学看法,不足之处还望批评指正.
1.原题呈现


图1
(Ⅰ)求证:AF∥平面BDE;
(Ⅱ)求证:CF⊥平面BDE;
(Ⅲ)求二面角A-BE-D的大小.
2.学生的困惑
困惑一:怎样才能找到二面角的平面角.
困惑二:如何求出二面角或其相应的三角函数值.
3.困惑的探究
二面角是通过定义来描述的,对定义的深刻理解是解题的基础,学生只有正确理解了定义,才能在头脑中想像并勾画出相应的几何图形,分解出解题需要的元素.因此,定义既是思维的基本元素,又是空间想像的出发点.教师应当抓住定义的本质特征和关键要素进行教学,弄清定义蕴含的解题途径.
从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,这两个半平面叫做二面角的面.从棱上的任一点出发,在两半平面内分别作与棱垂直的两条射线,这两条垂线所成的角的大小就是二面角的平面角.
我们可以发现通过定义将二面角这个空间中的角转化成了平面角,体现了数学将未知向已知转化的探究思路,同时应向学生强调找二面角的关键在于找两条与棱垂直的射线所成的角.定义法是“众法之源”,万变不离其宗,“树高千尺,叶落归根”,求二面角的一切方法起源于定义这个“根”!
法一:第(Ⅰ)、(Ⅱ)两小题解答略.
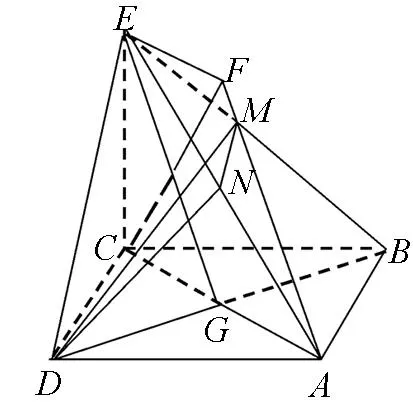
图2

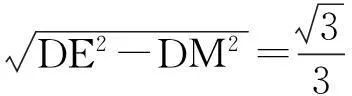
ΔEMN~ΔEBA,

上述解法密切结合定义,可以快速地找出二面角,便于学生容易理解与运用,可美中不足的是计算量太大,对解三角形的能力要求较高,学生解题过程中往往会出现难以为继的情况.该法通常应用于有一个半平面是直角三角形时比较合适,因为在求边时可用相似比转化.
上述解法貌似并不完美,可引导学生进一步完善.法一不足之处在于计算量,而究其原因是有一条垂直于棱的射线并不是半平面的高,那么引导学生考虑能否选择用另一条BE上的高来求二面角呢?事实上AB⊥BE,所以不难发现二面角与垂直于棱的两条异面直线DM与AB所成角存在关系.

图3
法二:由几何图形可得二面角A-BE-D为锐角,所以异面直线DM与AB所成角就是二面角A-BE-D的平面角.

法二将二面角与异面直线所成角建立了联系,让学生感受到“用数学”的成就感,但是似乎仍然要求较高,不能被多数学生所掌握,需要进一步简化完善.


法三大大简化了计算,也遵循了定义中发现的解题途径,让学生充分感受了数学的魅力以及活学活用所带来的乐趣,激发学生内在的探究欲望.

图4
法四:运用三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.虽然这个定理已从人教版中删除,但是我们可以通过证明线面垂直来达到相同的效果,因此本定理也提供了另一种添辅助线找二面角的一种途径.如图4,通常当点D在一个半平面内,过点D作另一半平面ABC的垂线,得垂足O;再过该垂足O作棱AB的垂线,得垂足E,连结得到斜线段DE,便形成了三垂线定理的基本构图(斜线DE、垂线DO、射影OE),通过证棱AB垂直平面DOE得AB⊥DE,AB⊥OE从而确定二面角的平面角,再解直角三角形求二面角的大小或其三角函数值.

图5

上述解法的优势在于计算量小,但是在找这个二面角的平面角的过程中思维量较大.教学中应强调抓住从一个半平面内点出发作另一个半平面的垂线这个解题关键,相信学生也能逐渐掌握这个方法.
以下是笔者在讲解方法五时的课堂实录.
生1:在应用法四的解题模型时,虽说我已明白解题关键,但是未必有能力找到并证明那个线面垂直,但是我发现若能求出半平面内点到另一个半平面的距离也可以求出二面角的正弦值,这样就避开了找垂足位置这个难点.
师:这个想法非常好,那么如何恰当地去求点到平面的距离呢?有没有同学能帮助他解决这个问题呢?
教室陷入了一片沉寂,终于有学生取得新发现.
生2:可以结合几何体的体积,因为在体积公式中可以转化出点到平面的距离.
师:想法真好!能用学过的知识探究新的知识领域,这是一个很棒的发现.那么大家能不能站在生2的“肩膀”上继续解决生1的困惑呢?
思考后,生3挠着头:虽说知道应联系体积,但我不知道该如何转化出所需的点到平面的距离.
班里很多同学表示认同,显然都有这个困惑.
师:同学们知道三棱锥有四个顶点,而这四点中的任一点都可看作三棱锥的顶点,所以一个三棱锥有四种表示,但体积相等.

师:这样做似乎还有漏洞,能否再补充一下.

师:很好!那么我想请同学来总结一下体积法在应用过程中的注意事项.
生5:体积法的妙处在于利用三棱锥的顶点变换来建立等量关系,转化得到点到平面的距离,然后应用法四中的数学模型解决二面角问题,最后还要注意二面角是锐角还是钝角.
正当笔者准备让学生总结二面角的所有常用解法时,一个学生要求展示他的解法.
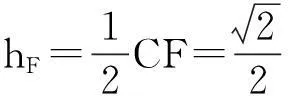
师:非常精彩的解法!那么请你说说你是怎么想到这个思路的.
生6:说来比较丢人,我当时未能正确使用体积法,但我发现AF∥平面BDE,那么我就利用它将距离转移到了F到平面BDE的距离hF.
师:生6很好地运用了数学中转化的思想方法,为问题的解决创造了可行条件,值得肯定.
在法五、法六的教学过程中,学生闪耀出智慧的光辉,令人动容.求二面角的方法还有很多,如面积投影法、空间向量法等等,笔者在此不再一一赘述.相信学生在理解本质的基础上,适当地加以练习巩固,二面角这个拦路虎就不难清除了.
4.几点思考
高中数学课程标准指出:“数学教学活动必须建立在学生的认知发展水平和已有的知识经验基础上.教师应激发学生的学习积极性,向学生提供充分经历数学活动的机会,帮助他们在自主探索和合作交流的过程中真正理解和掌握基本的数学知识与技能、数学思想和方法,获得广泛的数学活动经验.教师是数学学习的组织者、引导者与合作者.”
如何使数学课堂高效?这是每位数学教师都该积极探索的问题,也是新课改的目标之一.
4.1定义是数学解题的基础
很多学生不重视定义的理解,忽视了数学定义对解题的作用.可想而知,若是对定义总是似懂非懂的,对学生的学习肯定是十分不利的.因此,教师应该重视引导学生从数学的基本定义和知识出发,分析探索数学问题的解题途径,这不但能教给学生知识,而且在这个探索的过程中培养了学生的数学能力,例如转化化归、类比联想等等,这才是数学教学的根本.
4.2解学生之惑是实现高效课堂的手段
困惑是学生在课堂中的自然产物,教师若能敏锐地发现并及时地加以引导,就能提高学生的听课积极性和效率.与此同时,教师往往能在与学生的思维碰撞中擦出智慧的火花.因此,解学生之惑是实现高效课堂的有力手段.
4.3引领式教学是实现高效课堂的途径
引导学生在解决面临的问题中,主动获取和运用知识、技能,激发其学习主动性、自主学习能力和创造性解决问题的能力.该教学法以学生在教师的导学下自主合作完成学习任务,达成学习目标为宗旨.它不惟形而惟实,不惟新而惟效,把课堂的聚焦由“老师教得怎么样”转向“学生学得怎么样”,明确了衡量高效课堂的三条标准:即以学生“愿学不愿学”、“会学不会学”、学会没学会”为标准.一般操作步骤为自主探究的问题→合作探究的问题→质疑再探的问题→拓展创新的问题.
参考文献
[1]郭风禄.二面角求解策略——面面观[J].高中数理化,2012:14-18.
[2]李金兴.讲清数学道理揭示数学本质[J].中学教研(数学),2013(1):7-8.
