基于求解速度势通量的指定压力分布二维翼型设计方法

周 斌，唐登海

（中国船舶科学研究中心，江苏无锡214082）

基于求解速度势通量的指定压力分布二维翼型设计方法

周 斌，唐登海

（中国船舶科学研究中心，江苏无锡214082）

为了提升翼型的水动力和空泡等性能，指定压力分布的翼型剖面设计的方法多数集中在给定攻角下的翼型剖面的设计，该方法存在计算量较大，收敛性不理想，特别是推广到三维问题时，上述问题尤为突出，限制了翼型设计的进一步发展。文章以势流理论面元方法为基础，通过求解指定压力分布条件下翼型表面的速度势通量，获得翼型表面形状的修正量，并将修正量分解为攻角的变化以及剖面自身的变化两部分，从而得到了翼型唯一的设计攻角和翼型剖面几何（厚度分布、拱度分布）。文中采用上述方法对二维翼型问题进行了设计验证，表明该方法可以设计任意指定压力分布的翼型剖面，理论上该方法可以用于全三维翼型的设计问题。

翼型设计；指定压力分布；势流理论；新型翼剖面

0 引 言

翼型表面的压力分布决定了翼型的流体动力特征，对于水翼来说，为了提升翼型的水动力和空泡等性能，人们一直希望能够设计出指定压力分布的翼型几何剖面。

指定任意压力分布的翼型剖面设计方法已经发展多年。Kennedy和Marsden（1978）[1]通过二维流函数求解法，在二维翼型表面采用涡层密度分布代替翼型剖面，获得了指定攻角下，任意压力分布的翼型剖面。Eppler和Shen（1979）[2]采用了保角变换的思想提出了在指定攻角下任意压力分布的翼型剖面设计方法。

上述设计方法只适用于二维翼型剖面的设计。为了更精确地模拟物体表面，苏玉民[3]采用面元法，在指定攻角条件下，通过求解控制点上几何的细微扰动对翼型剖面流动的影响，获取雅可比影响矩阵，然后对原始剖面进行修改达到指定的压力分布；李俊华[4]基于同样的思想，采用B样条来重新表达翼型剖面，通过改变控制点来调整翼型剖面的几何，建立翼型剖面几何与翼形表面压力分布的关系，最终获得满足给定压力分布的翼型剖面。上述关于翼型的设计方法都以面元法为基础，可以在指定攻角条件下设计三维翼型的剖面。但是上述方法需要计算雅可比矩阵，计算量很大，假设三维翼型表面网格划分N个，为获得雅可比修正矩阵需要对N个面元分别进行一次正问题计算。如果需要迭代m次，则计算量正比于mO（N2），因此上述方法如果推广至更复杂的全三维问题，需要的计算量往往会很大。

Lee Chang-Sup（1994）[5]采用面元法求解指定攻角、指定压力分布情况下，翼型表面的速度势通量，然后修改原始翼型剖面获得满足设计要求的翼型剖面，并对二维问题和三维的翼型设计问题进行计算，上述方法将翼型几何的求解问题转换成求解速度势通量，因此求解一次翼型设计问题的工作量等于同样求解一次正问题，m次迭代的计算量为mO（N），较以往求解雅可比矩阵修正翼型剖面的方法减小了一个量级的计算量。

以上介绍的方法虽然采用不同的原理，但是都是在解决求解给定攻角、给定压力分布的设计问题。我们知道一个具有固定型值的翼型，在指定攻角下，其压力分布是唯一的。反过来我们思考这样的问题，如果给定了一种压力分布，那么相应的翼型剖面和攻角是否是唯一的？

按照以往的给定攻角、给定压力分布翼型设计方法，显然认为同样的压力分布可以有不同翼型和攻角的组合。本文以此为切入点，在Lee Chang-Sup（1994）[5]的基础上，尝试将翼型变化的修正量分解为翼型攻角的变化和翼型自身的修正量，这样可以在翼型设计时获得唯一的翼型的攻角和翼型剖面几何（厚度分布、拱度分布）。数值计算表明本文方法较好地还原了给定压力分布的翼型剖面和攻角，同时适用于任意指定压力分布的翼型设计问题，并且原理上适用于三维翼型的设计问题，为面元法全面应用于翼型设计问题提供了新的思路。

1 设计计算方法

1.1 设计方法原理

由势流理论可知，对于无界、无旋、定常、不可压和无粘理想流体的有升力体绕流问题，流域内的扰动速度势可用下式表达：

其中：Sb表示物体表面，Sw表示有升力体的泄出涡表面即尾涡面，S∞表示无穷远处流体域界面，G表示格林函数，如图1所示，无穷远处扰动速度势对物体表面的影响可视为一个常值速度势φ0，于是（1）式可写成

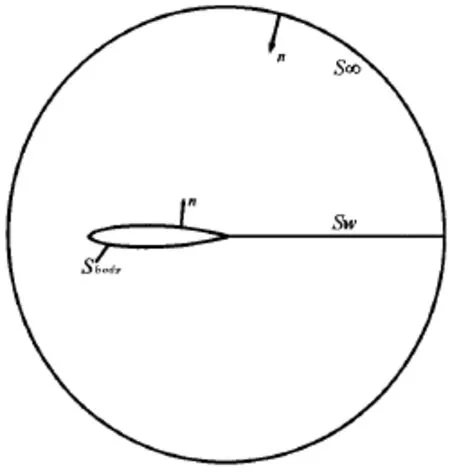
图1 有升力体面元法流体计算域示意图Fig.1 Definition sketch for lifting surface method

（2）式就是常见的求解正问题的基于扰动速度势的面元法方程，由于扰动势可以表示为流体域总速度势与来流速度势的差，即有下式：

对于给定物体表面的压力问题，可以根据伯努利方程求解物体表面的速度分布，通过求解速度分布在物体表面的积分获得物体表面的总的速度势：

其中：vc表示物体表面沿主流方向（弦向）的速度分布。对于设计问题，由于物体表面的压力分布是指定的，因此其给定的Φsb也是指定的，将指定的Φsb代入（8）式时，可以求解方程中的未知项，其中的物理意义为指定压力分布时，翼型表面的速度势通量值。

对于翼型设计问题，为了获得调整后翼型剖面的攻角和翼型几何参数，将翼型表面的调整量分为两部分共同作用的结果。一部分是翼型攻角的作用；另一部是翼型几何参数的变化。于是得到了如下翼型攻角α和翼型剖面自身的修正量Δt的计算公式：

其中：s_trail为翼型随边位置；s_lead为翼型导边位置；s（x）为控制点弦向位置到随边的距离。

此外对于有升力翼型剖面的面元法求解问题，需要在翼型随边尾缘给定库塔条件，对于翼型剖面问题可采用速度势库塔条件[6]，即：

此外（8）式中还存在未知量φ0，需要补充方程使得方程（8）获得唯一解，根据调和函数性质，补充方程的物理描述为在满足给定压力分布后，所有物体表面的速度势通量与面元面积的乘积和为0，即有如下方程：

至此通过求解方程（8）、（10）、（11）、（12）式和（13）式，就可以获得指定压力分布下确定的翼型几何参数和翼型攻角。

1.2 数值离散方程

（8）式是对一般问题的描述，对于二维翼型剖面的设计问题，可以沿翼型表面划分Np个单元，为保证计算精度以及获得光滑的翼型剖面，采用余弦划分形式，以保证网格在导边和随边附近加密。此时对于每一个网格单元，（8）式可以离散为

求解线性方程组（15）便可以求解每个翼型网格上的通量变化量，尔后根据（10）式、（11）式对翼型剖面进行修改迭代，最终可得到满足指定压力分布的翼型剖面。

2 验证算例

2.1 已知翼型压力分布的翼型参数复原

为了验证本方法求解的翼型剖面及攻角是唯一的，对已知翼型剖面几何的二维翼型剖面设计问题进行了算例验证。

首先采用二维扰动速度势面元法对NACA0025翼型在2°攻角条件下的压力分布进行了计算，然后将该压力分布赋值给NACA0010，0°攻角的翼型，开始数值迭代设计。为了获得精细的物体表面几何特征，对翼型剖面弦向划分了100个直线单元。

NACA0010，0°攻角的翼型剖面与迭代过程剖面的压力分布见图2，NACA0010，0°攻角的翼型几何与NACA0025，2°攻角翼型几何及迭代过程剖面几何见图3；从图2、图3可以看出，采用本方法经过3次迭代后的翼型几何与目标翼型几何便具有良好的重合度。数值测试共迭代了10次，获得的翼型剖面攻角收敛在2.07°附近与设计目标值NACA0025，2°的给定值非常接近。

图2 NACA0010，0°攻角翼型至NACA0025，2°攻角翼型的压力分布迭代过程Fig.2 Iterative process of pressure distribution from NACA0010 airfoil at 0 deg to NACA0025 at 2 deg

图3 NACA0010，0°攻角翼型至NACA0025，2°攻角翼型的几何迭代过程Fig.3 Iterative process of section geometry from NACA0010 airfoil at 0 deg to NACA0025 at 2 deg

通过上述算例的验算，较好地复原了已知翼型压力分布情况下原翼型的几何参数，也说明了在指定压力分布情况下，可以获得唯一的翼型剖面和相应的攻角。

2.2 指定压力分布的翼型剖面设计

为了获得翼型表面更好的流动形态，在翼型设计中希望得到指定压力分布形式的翼型参数。我们以NACA0010翼型在攻角3°时的翼型压力分布为基础，指定了新的翼型压力分布形态，见图4。其中“NACA0010，α=3°”表示NACA0010翼型在攻角3°时翼型表面压力分布；“Target Cp”表示指定的目标压力分布形态（抑制翼剖面导边的负压峰值）。以此为目标压力，应用本文介绍的方法进行翼型的设计。

图4 指定的压力分布与母翼型的压力分布Fig.4 The specified flat rooftop pressure distribution and the original pressure distribution of NACA0010 at 3 deg

图5 翼型参数随着迭代过程的变化趋势Fig.5 Iterative process of the airfoil parameters

首先以3°攻角NACA0010翼型为母翼型，对翼型剖面弦向划分了100个直线单元，然后迭代计算获取满足指定压力分布要求的翼型剖面。对迭代过程中获取的翼型剖面的攻角、最大拱弧和最大厚度进行提取，可以获得翼型参数随着迭代过程的变化趋势，见图5。其中α表示攻角，fmax表示翼型剖面的最大拱度，tmax表示翼型剖面的最大厚度。从翼型参数的变化可以看出，在进行3次迭代后翼型参数便趋于收敛。迭代过程产生的翼型几何见图6，翼型导边局部几何见图7，相应的翼型表面压力分布变化见图8。经过10次迭代后满足指定压力分布要求的翼型攻角为2.54°，最大拱度比为0.011，最大厚度比为0.116。

图6 迭代过程产生的翼型几何Fig.6 Iterative process of section geometry

图7 迭代过程翼型导边局部几何Fig.7 Close view of the leading edge geometry

图8 迭代过程中翼型表面压力分布变化Fig.8 Iterative process of pressure distributions

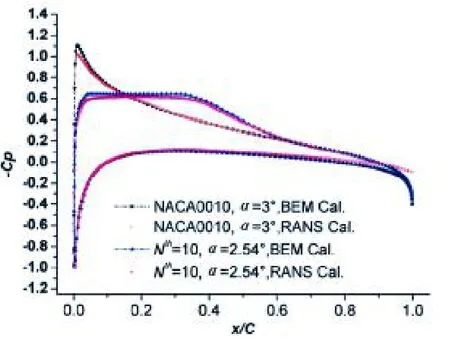
图9 面元法（BEM）和RANS方法对翼型压力分布的计算结果Fig.9 Comparisons of pressure distributions obtained from BEM and RANS methods for the design airfoil

图10 指定的“锯齿形”的压力分布Fig.10 The specified‘zigzag'pressure distribution compared with baseline NACA0010 airfoil at 3 deg

图11 满足“锯齿形”的压力分布的翼型几何Fig.11 Designed section geometry with‘zigzag'pressure distribution compared with baseline NACA0010 airfoil

由于上述获得的满足指定压力分布翼型几何参数是全新的，除了采用面元法对其压力分布进行数值计算外，我们还采用RANS方法对母翼型和设计翼型的压力分布形态分别进行了数值计算。两种方法的计算结果见图9。从RANS和面元法的计算结果对比可以看出，在（0.0～0.9）弦长区域内RANS方法和面元法计算的压力分布主要特征一致，重合较好，在随边（0.9～1.0）弦长区域，压力分布有一些区别，这个区别主要是因为面元法是基于势流的计算方法，没有考虑边界层的影响。通过两种方法的计算对比可以看出采用本方法可以较准确地获得满足指定压力分布的翼型。

在完成上述指定压力分布翼型的剖面设计后，为了考察本方法的稳定性和适用性，我们还对更加“特殊”的指定压力分布进行了翼型设计。“特殊”的指定压力分布见图10，从其压力分布可以看出，给定的压力分布在翼型上表面存在 “锯齿形”的压力分布区域。仍以NACA0010翼型为母翼型，迭代10次后获得的翼型剖面见图11。仍采用RANS方法和面元法分别对设计得到的翼型的压力分布形态进行了数值计算，两种方法的计算结果见图12。从两种计算得到的压力分布可以观察到所计算的翼型上表面也存在“锯齿形”的分布形态，说明本方法具有较好的适应性。

通过上述算例的验算，可以看出本方法适用于任意指定压力分布设计问题的求解。

图12 面元法（BEM）和RANS方法对设计翼型压力分布形态的计算结果Fig.12 Comparisons of pressure distributions obtained from BEM and RANS methods for the design airfoil

3 结论与展望

本文以势流理论、总速度势面元方法为基础，通过求解指定压力分布设计问题物体表面的速度势通量，将翼型剖面的修正量分为因攻角变化引起的改变和翼型剖面自身改变两个部分，由此在指定压力分布的条件下，可以获得唯一的翼型几何参数和攻角，为面元法应用于翼型设计问题提供了新的思路。

数值验算结果表明，本方法可以较好地复原给定压力分布的翼型剖面，同时本方法也适用于任意指定压力分布翼型设计问题求解。

从求解方法的计算量分析，本方法从基于扰动速度势的面元法方程推导得出，因此在翼型设计时，不需要计算压力分布与几何变化之间的雅可比矩阵，计算量与面元法求解正问题处于一个量级。同时数值算例表明，本方法收敛性很好。

从求解方法的原理上分析，本方法如果将（8）式中格林函数项取为三维格林函数，可以应用于三维翼型的设计问题以及其他三维流动问题的设计，作者正在开展这方面的设计与应用研究。

[1]Kennedy J L,Marsden D J.A potential flow design method for multicomponent airfoil sections[J].Journal of Aircraft,1978, 15(1):47-52.

[2]Eppler R,Shen Y T.Wing sections for hydrofoils-part 1:Symmetrical profiles[J].Journal of Ship Research,1979,23(9): 209-217.

[3]Su Yumin,Ikehata M,Kai H.A numerical method for designing three-dimentional wing based on surface panel method[J]. Journal of the Society of Naval Architects of Japan,1997,182(1):39-46.

[4]Li Junhua,Tang Denghai,Dong Shitang.Propelelr design by prescribed pressure distribution[J].Journal of Ship Mechanics, 2010,14(2):10-19.

[5]Lee Chang-Sup,Kim Young-Gi,et al.A surface panel method for design of hydrofoils[J].Journal of Ship Research,1994, 38(9):175-181.

[6]Morino L.Subsonic potential aerodynamics for complex configurations-A general theroy[J].AIAA Journal,1974,12(2): 191-197.

A design method for 2-D hydrofoil by the specified pressure distribution based on velocity potential flux of the surface

ZHOU Bin,TANG Deng-hai
(China Ship Scientific Research Center,Wuxi 214082,China)

In order to improve the hydrodynamic and cavitation performance of the hydrofoil,some hydrofoil section design methods with specified pressure distribution are developed.However the section is designed at a given angle of attack in the most of such methods,which may result in large computation cost and difficulties in convergence especially when the methods are extended to 3-D problems.In the paper,a new 2-D hydrofoil section design method is proposed based on surface panel method of the potential theory.The velocity potential flux and geometric corrections of the blade surface can be obtained by solving total velocity potential equation with specified pressure distribution on the blade surface.The geometric correction could be decomposed into two parts.One is owing to the change of angle of attack,and the other is the change of profile itself.In this way,the unique design angle of attack and section geometry for specified pressure distribution can be attained.The numerical results show that the method is robust and valid.

hydrofoil profile design;specified pressure distribution;potential theory;new blade section

U661.1

：Adoi:10.3969/j.issn.1007-7294.2016.04.003

1007-7294（2016）04-0403-07

2015-07-07

周 斌（1986-），男，工程师，E-mail:htrmax@163.com；唐登海（1965-），男，研究员，博士生导师。