基于MQ插值的变形网格在船舶阻力预报中的应用

邵 菲，杨东梅，刘致豪，李创兰

（哈尔滨工程大学船舶工程学院，哈尔滨150001）

基于MQ插值的变形网格在船舶阻力预报中的应用

邵 菲，杨东梅，刘致豪，李创兰

（哈尔滨工程大学船舶工程学院，哈尔滨150001）

在非结构切分网格的框架下，发展了一种基于Multi-Quadric插值的变形网格技术，结合CFD软件STARCCM+，采用SST湍流模型，并以VOF法进行自由液面的追踪，将该变形网格技术应用于带附体穿浪双体船的阻力预报中。分别以网格的拉伸变形和斜率变形实现了阻流板和尾楔的边界运动，计算了阻流板高度为4 mm、6 mm和8 mm以及尾楔角度为5°、10°和15°时的工况。计算结果表明，变形网格方法与固定网格方法取得了相同的精度；同试验值相比，在不同工况下变形网格最大平均误差约为6.67%，验证了其可行性。但是，相比于固定网格方法，变形网格方法的计算时耗最大可减少40%，因此采用该变形网格方法可极大地提高带可变形附体的船舶的阻力预报效率。

Multi-quadric插值；网格变形；阻流板；尾楔；计算时耗

0 引 言

阻流板与尾楔是常见于船舶艉部的减阻附体，它们通过改善船舶航行过程中的尾部流场来达到提升船体阻力性能的目的。现有资料大多采用模型试验或CFD手段来对这两种附体的水动力特性进行研究；其中CFD手段不需要进行实体模型的建造，以及相应的时间、人力和物力的投入，较模型试验具有更好的时效性，因而得到了广泛的采用。哈尔滨工程大学的马超[1]和邓锐[2]等人，即采用CFD手段对加装于滑行艇和双体船上的阻流板以及尾压浪板进行了研究。

阻流板或尾楔的形状对其水动力特性有着至关重要的影响，在传统的CFD计算方案[3-4]中，为了得出较优的附体外形，需要针对不同的附体外形进行网格划分，并重复由计算初始化到计算收敛的全部迭代过程。整个计算流程中，需要较多人工干预以及重复工作量，效率较低。

而变形网格则可在求解过程中通过改变网格节点坐标来达到控制边界形状的目的，省去了网格的重新划分、流场求解的初始化以及相应的收敛时耗，因而具有较高的计算效率。目前的变形网格技术主要应用于飞行器的运动模拟[5]、机翼变形（结冰）[6]、鱼体仿生[7]等方面，均取得了较好的模拟效果。在此基础上本文提出了一种基于multi-quadric（MQ）[8]插值法的网格变形技术，并将其应用于某型穿浪双体船的阻流板及尾楔的变形控制，从而提高静水阻力计算的效率。

1 基于MQ插值的变形网格基本原理

1.1 MQ插值基本原理

Multi-quadric函数是径向基函数的一种，通常简记为MQ函数，MQ函数在地球物理学、测绘学、数字地形模拟及水文学诸方面都有广泛的应用。基于MQ函数插值问题的描述如下，对于给定数据点集：，寻找函数

满足插值条件

而基于MQ插值的变形网格技术，其基本原理则是通过一系列的控制点来完成变形网格对网格节点的初始运动的控制。每一个控制点被赋予一个用来移动邻近网格节点的位移矢量。这些特定的位移值利用MQ插值法在进行变形的整个区域内进行插值，即可得到各网格节点的位移。

式中：为两节点的距离，cj为为一个基础常量，本文中该常量取为0。该方程满足：

1.2 阻流板网格变形策略

在网格变形中，运动边界（变形附体）上的每一个控制点都对应一个特定的位移矢量，该位移矢量将决定每一个时间步长内该控制点的移动距离和方向，将该位移转化为各节点的运动速度，即可实现边界的变形。

对阻流板来说，其在工作时一般是沿垂直于船底的方向运动，其运动形式可以看做是变形边界沿一个或多个方向的延伸，即拉伸变形。如图1所示，经过时间T，几何体的边界L1、L2、L3拉伸变形为L1′、L2′、L3′，其变形量为Δs，相应节点的运动速度为：

式中：θ为变形边界与坐标轴的夹角。

1.3 尾楔网格变形策略

尾楔的运动形式可以看作是运动边界与固定边界之间的夹角发生改变，即运动边界进行斜率变形。如图2所示，变形边界L1进行斜率变形，经过时间T后，其与L2之间的夹角发生了变化，而L3则相应地做拉伸变形，拉伸变形量为Δs。各控制点可认为仅沿x方向运动，其速度为：

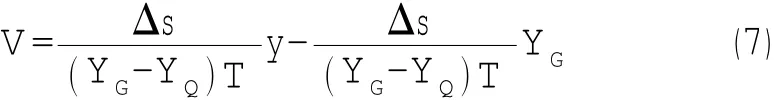
式中：YG和YQ分别为顶点G和Q在y方向上的坐标值，可以看出控制点的移动速度为一个与控制点y方向位置有关的线性函数。

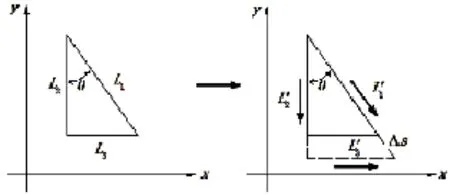
图1 拉伸变形示意图Fig.1 Schematic diagram of tensile deformation

图2 斜率变形示意图Fig.2 Schematic diagram of slope deformation

2 数值船池的建立

2.1 数值计算方法

本文采用通用CFD软件STAR-CCM、利用RANS（Reynolds-Averaged Navier-Stokes）方程方法对一穿浪双体船的黏性绕流场进行模拟，所求解的连续性方程和动量方程如下：

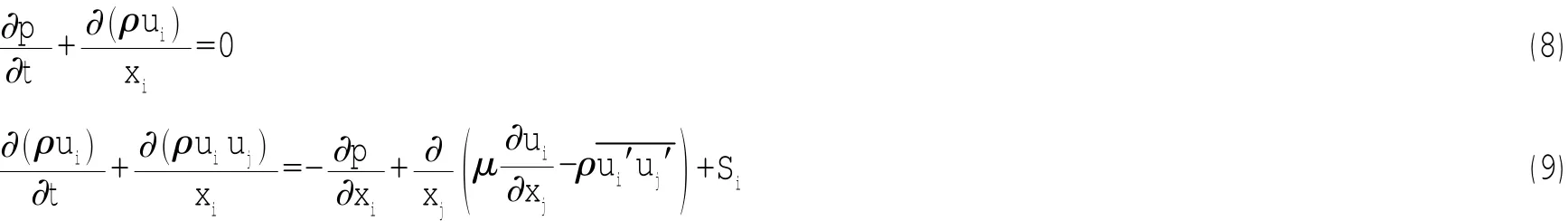
式中：ui，uj为速度分量时均值；p为压力时均值；ρ为流体密度；μ为动力粘性系数；ρui′uj′为雷诺应力项。选取SST（Shear Stress Transport）湍流模型来封闭RANS方程，并以VOF（Volume of fraction）法来实现流域内水气两相流的划分和自由液面的追踪。

2.2 计算模型

本文中所研究的对象为一穿浪双体船，其外形如图3所示；阻流板和尾楔均安装于艇艉，且宽度与片体宽度相同，其安装形式如图4所示。表1中则给出了模型的主要尺度参数。

2.3 网格划分及边界条件

计算域的尺寸对计算的收敛时间和精度都有很大的影响，本文中考虑到双体船模型的对称性，计算域只针对一侧的片体进行建立；其入口处距船艏1倍船长，出口处距船尾3倍船长，上下边界分别距船体0.8倍船长和1倍船长，自船体向外侧延伸1.5倍船长。边界条件的设置如下：

入口：指定来流速度，即为船模试验中各速度点所对应的船速；

对称面：采用对称边界条件；

出口：出口处指定压力分布为静压；

船体：不可滑移壁面；

其他壁面：滑移壁面。

本文采用切分网格对整个计算域进行离散，其中船体表面网格尺寸取船长的5‰，最大体网格尺寸则为5%船长。在船体近壁面和自由液面处进行了网格的加密；其中船体近壁面网格的无量纲厚度y+的取值范围为20～150，自由液面体网格尺寸为1%船长，总网格数量约为110万。计算域的网格划分及阻流板和尾楔处的网格形式如图5所示。

图3 穿浪双体船计算模型Fig.3 Calculation model of wave piercing catamaran

图4 阻流板及尾楔的安装形式Fig.4 Installation forms of interceptors and stern wedge

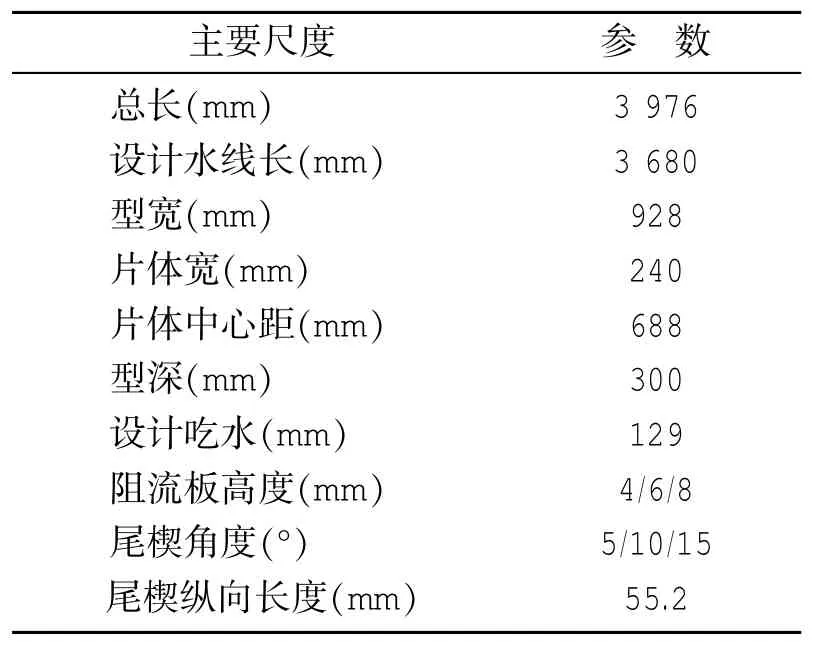
表1 计算模型主要尺度参数Tab.1 The principal parameters of calculation model

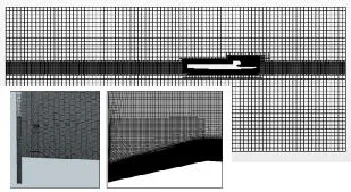
图5 计算域及阻流板和尾楔上的网格划分Fig.5 Mesh generation in interceptors,stern wedge and calculation domain

3 计算结果及分析

3.1 带阻流板模型的计算

基于拉伸变形的不同高度阻流板下船体阻力计算的基本思想是：只建立一个带有初始高度的阻流板的船体模型，对该高度阻流板下的模型进行计算，计算完成后在当前流场环境下，利用拉伸变形将阻流板高度改变，进行第二个工况下的计算。以此类推，该航速下阻流板不同高度的工况由一次计算完成。

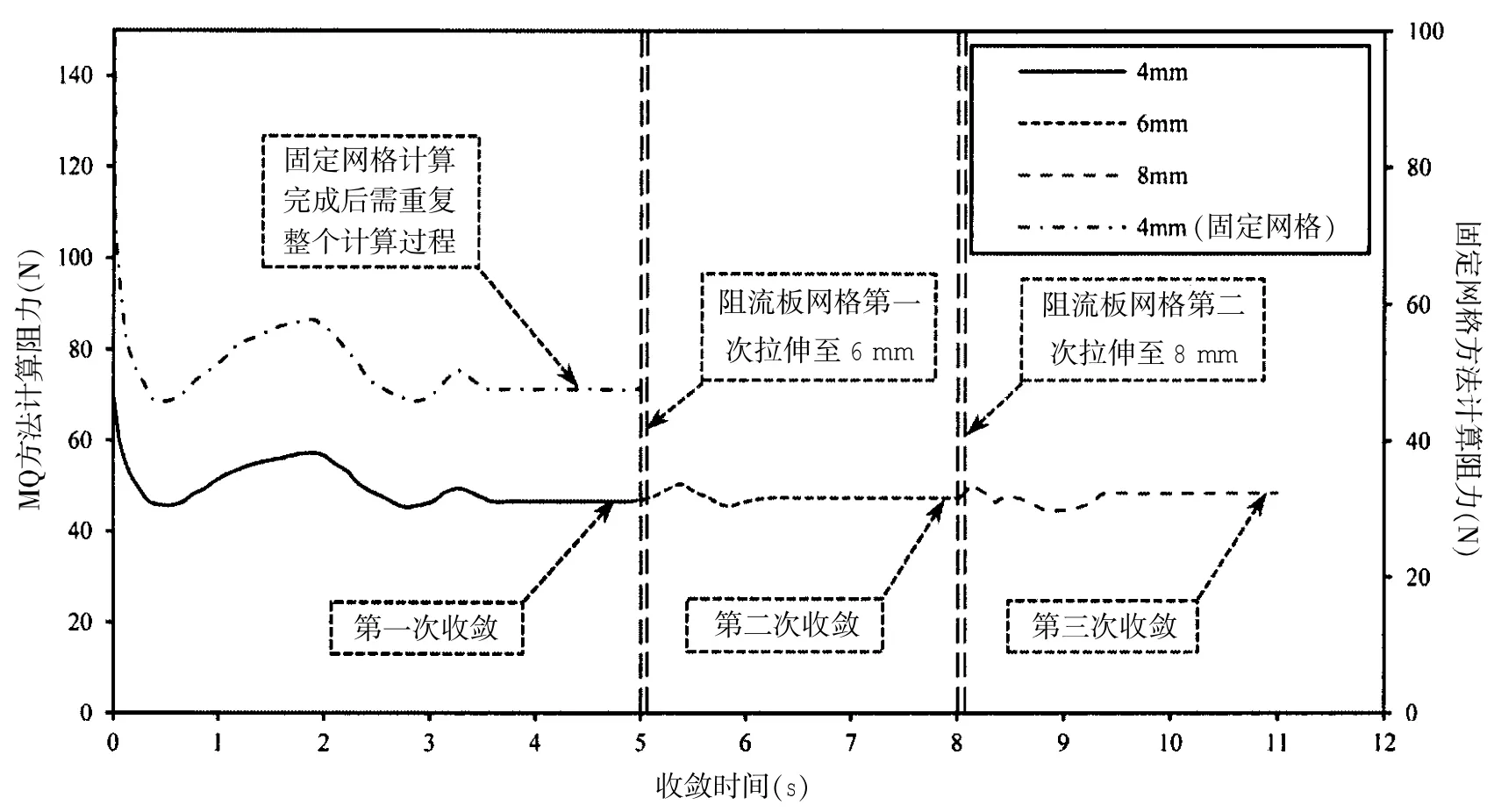
图6 利用MQ方法计算不同高度阻流板时的收敛时历曲线Fig.6 Convergence time history curves of calculation results by using MQ method in different height of interceptors

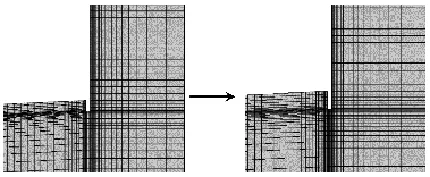
图7 阻流板网格拉伸前后对比Fig.7 Comparison of grid changes before and after extension in interceptors

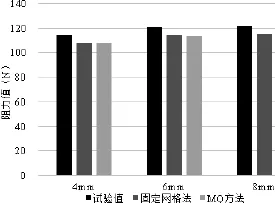
图8 两种方法在计算不同阻流板高度模型时的精度对比Fig.8 Accuracy comparison of calculation in different heights of interceptors by two different methods

采用MQ方法计算的收敛历程如图6所示，初始给定阻流板高度为4 mm的计算模型，对其进行网格划分，计算至第一次稳定收敛时的物理时间为5 s；此时进行网格拉伸，如图7所示，经过0.1 s后，阻流板高度变为6 mm；再次计算至8 s时，计算第二次收敛；再次拉伸阻流板网格，阻流板高度变为8 mm；最终在11 s时，完成计算的第三次收敛。图6中同时给出了固定网格方法单次计算的收敛历程，可以看出，采用固定网格方法的单次计算收敛时间同样也为5 s，但之后的计算需要重复网格划分和相同的计算过程，因此采用MQ方法后整体的计算效率有了明显提高。

图8中给出了在航速为4.84 m/s的航速下，两种方法所计算的不同阻流板高度模型的阻力与试验值的对比，可以看出，MQ方法在网格变形之后仍能取得与固定网格法相当的计算精度；在4 mm、6 mm和8 mm高度的阻流板的工况中，两种方法的计算误差分别为5.86%和5.86%、5.84%和5.18%以及5.79%和5.55%。而在不同航速下MQ方法计算值与试验值的对比也表明该方法对应于不同工况均具有较好的可行性，如图9所示，在4 mm、6 mm和8 mm高度的阻流板的工况中，其平均误差分别为6.22%、6.67%和6.20%。

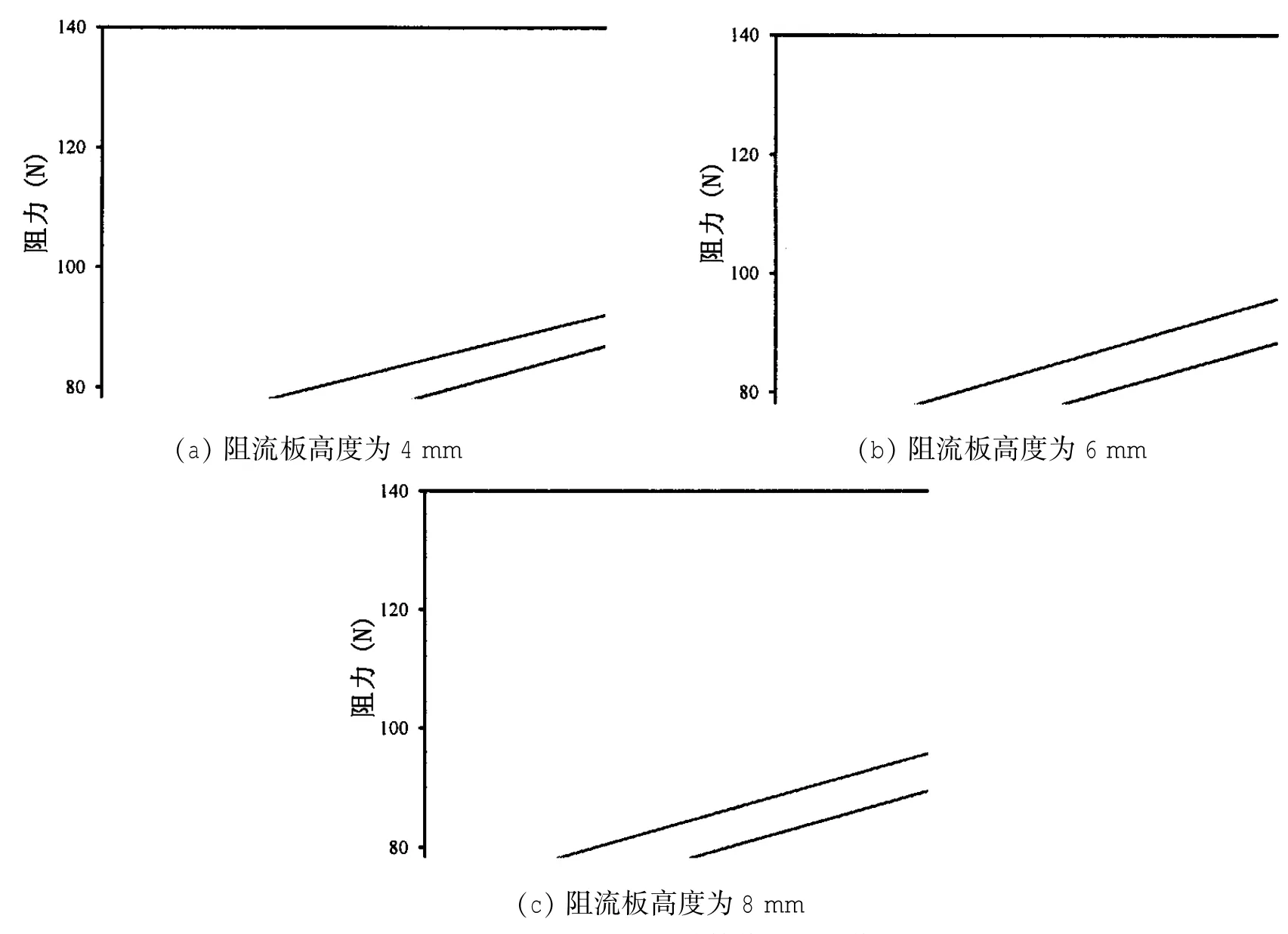
图9 不同航速下MQ方法计算值与试验值的对比Fig.9 Comparison between calculated values by using MQ method and experimental values in different speeds

3.2 带尾楔模型的计算

带尾楔模型的计算思想与带阻流板模型的基本相同，即在计算收敛之后利用网格的斜率变形改变尾楔的角度。其收敛时历如图10所示，可以看出经过两次历时0.1 s的斜率变形之后（如图11），根据由（7）式所计算的节点变形速度，尾楔角度由5°变为15°，历次计算均达到收敛要求，总的计算时间仍为11 s，计算效率要优于固定网格法。

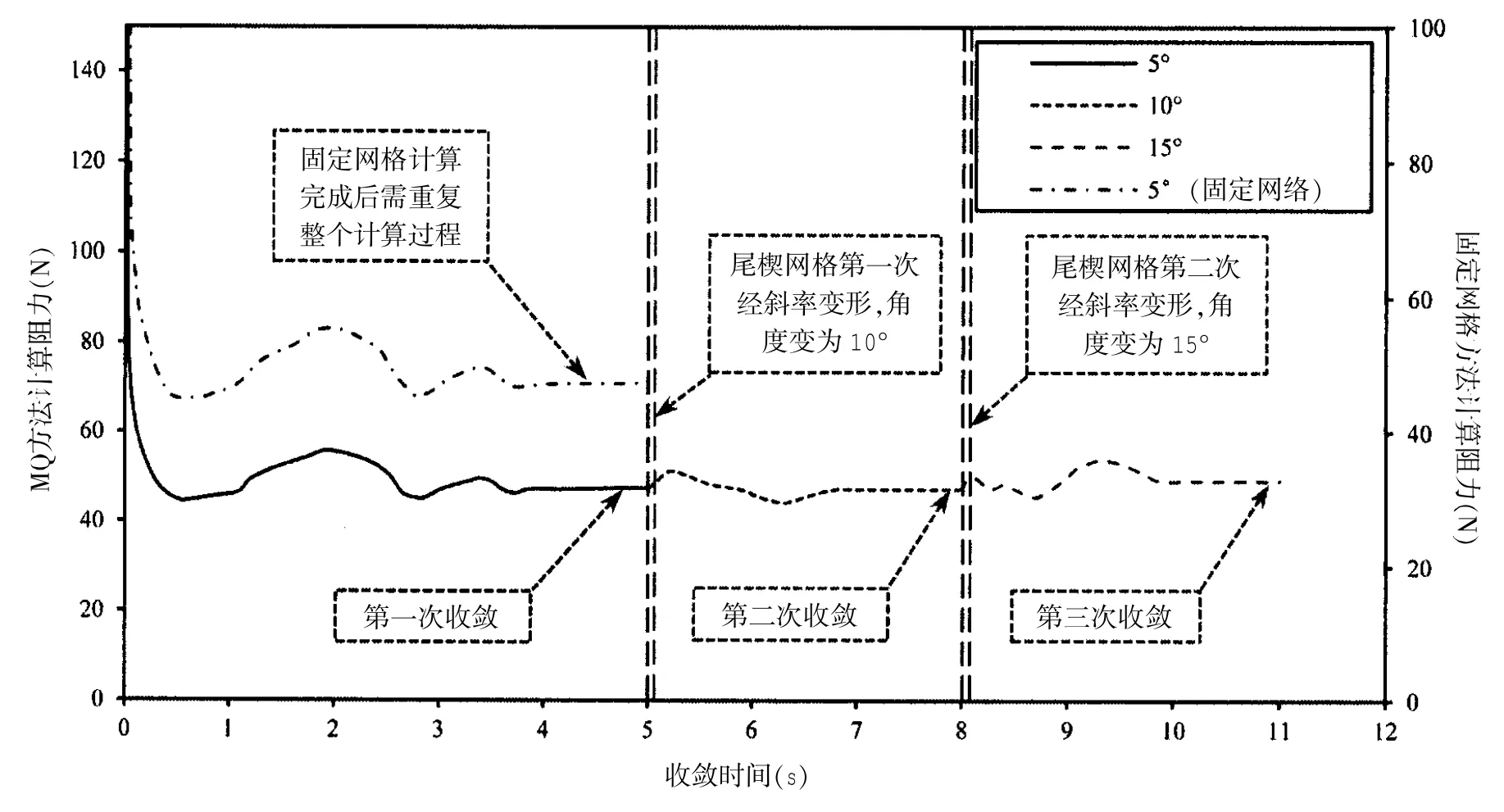
图10 利用MQ方法计算不同尾楔角度模型时的收敛时历曲线Fig.10 Convergence time history curves of calculation results by using MQ method in different angles of stern wedge

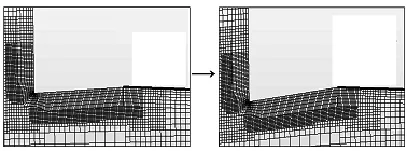
图11 尾楔网格斜率变形前后对比Fig.11 Comparison of grid changes before and after slope deformation in stern wedge

两种方法计算精度的对比如图12所示，图13则给出了MQ方法计算值在不同工况下与试验值的对比，可以看出在计算带尾楔模型的阻力时，MQ方法在计算精度上与固定网格法相差依然不大；而在5°、10°和15°尾楔的工况中，其相对于试验值的平均误差分别为3.97%、4.17%和6.25%，这表明该方法在尾楔变形的计算中仍然具有较好的可行性。

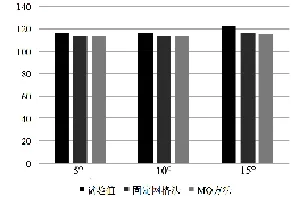
图12 两种方法在计算不同尾楔角度模型时的精度对比Fig.12 Accuracy comparison of calculation in different angles of stern wedge by two different methods

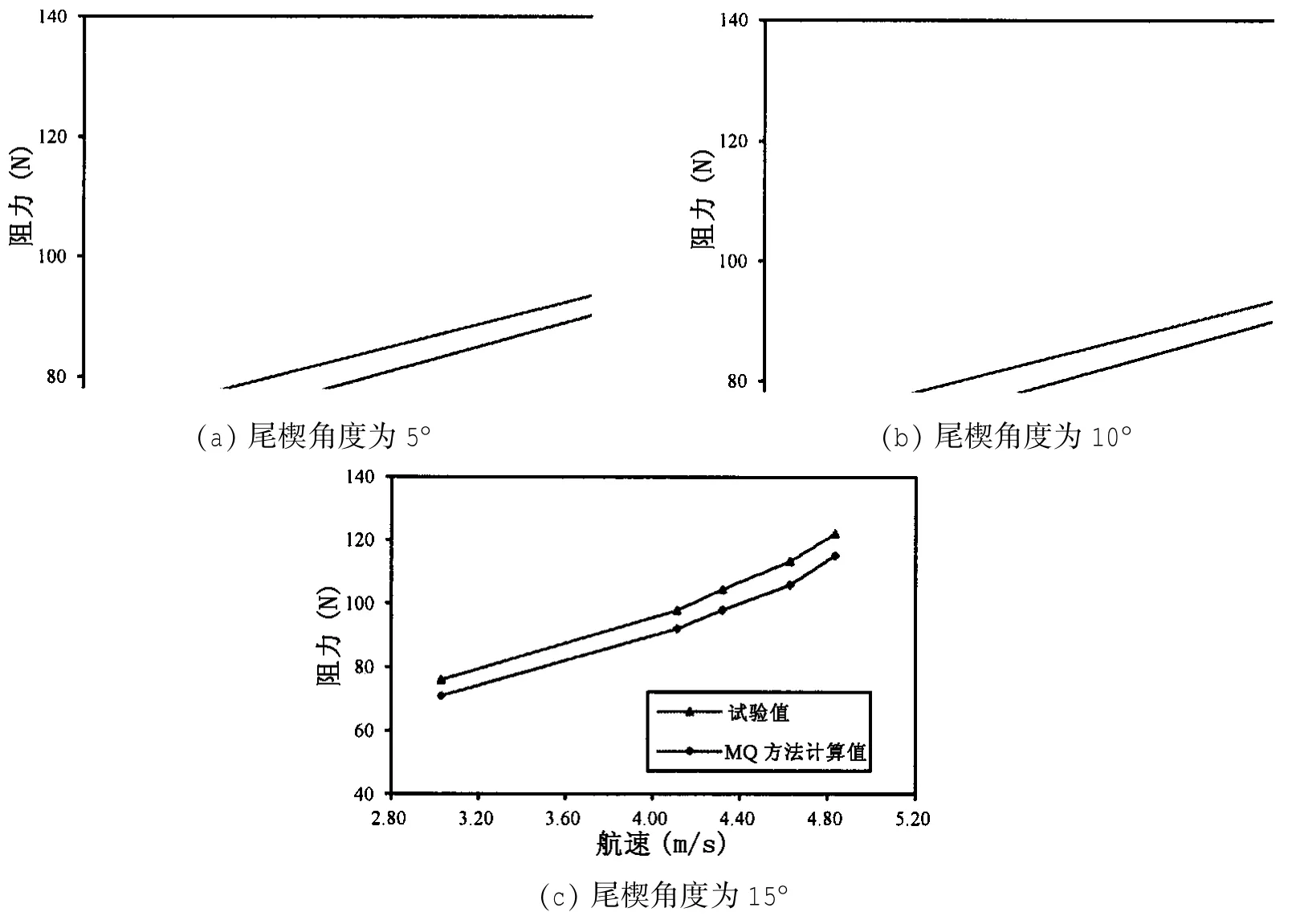
图13 不同航速下MQ方法计算值与试验值的对比Fig.13 Comparison between calculated values by using MQ method and experimental values in different speeds

3.3 MQ方法计算效率分析

根据以上计算结果可以看出，MQ方法在初始网格的计算中同固定网格法相同，达到收敛的物理时间为5 s，而网格变形后达到收敛的物理时间均为3 s。在相同的计算条件下，收敛的物理时间即可反映出计算实际的时间消耗，因此可得出MQ方法相对于固定网格法的计算时耗收益δ为：式中：M为计算所需考虑的速度点的个数，N则表示附体方案的个数。可以看出，附体方案个数越多，相应的时耗收益也就越大，在本文判定收敛的物理时间的基础上，其最大值为40%。

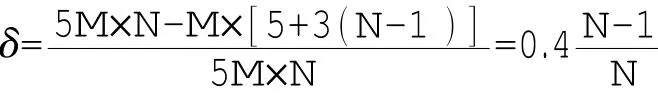
4 结 论

本文将基于MQ插值的变形网格应用于带阻流板或尾楔的穿浪双体船的阻力计算中，采用MQ函数构建了各网格节点的位移插值函数，并以拉伸变形和斜率变形这两种网格变形方式实现了动边界的运动，根据本文的分析可得出以下几点结论：

（1）基于MQ插值的变形网格取得了与固定网格法相当的精度，与试验值的对比也表明该方法在不同工况下均有较好的可行性。

（2）基于MQ插值的变形网格可有效提高多附体方案CFD计算的效率，相对于固定网格法，其最大时耗收益为40%。

（3）除阻流板和尾楔之外，根据基于MQ插值的变形网格中边界的运动特性，该方法还可应用于T型水翼浸湿调整、多体船片体间距改变、尾压浪板和压浪条下压角度的变化等附体变形的计算中。

[1]马 超.阻流板和尾压浪板对滑行艇阻力性能影响[D].哈尔滨:哈尔滨工程大学,2012. Ma Chao.The effect of interceptor and stern flap on the resistance of planning boat[D].Harbin:Harbin Engineering University,2012.

[2]邓 锐.阻流板对双体船水动力性能影响的数值研究[D].哈尔滨:哈尔滨工程大学,2010. Deng Rui.Numerical research on influence of the interceptor on catamaran hydrodynamic performances[D].Harbin:Harbin Engineering University,2010.

[3]邓 锐,黄德波,周广利,等.带有阻流板的双体船水动力性能数值研究[J].华中科技大学学报（自然科学版）,2011 (4):97-110. Deng Rui,Huang Debo,Zhou Guangli,et al.Numerical research on hydrodynamic performance of catamarans with interceptors[J].Journal of Huazhong University of Science and Technology(Natural Science Edition),2011(4):97-110.

[4]邓 锐,黄德波,周广利,等.阻流板水动力机理的初步计算研究[J].船舶力学,2012,16(7):740-749. Deng Rui,Huang Debo,Zhou Guangli,et al.Preliminary numerical research of the hydrodynamic mechanism of interceptor[J].Journal of Ship Mechanics,2012,16(7):740-749.

[5]黄守智,李 杰,蒋胜矩,等.基于变形网格技术的非定常流动数值分析方法研究[J].导箭与制导学报,2005,25(3): 186-188. Huang Shouzhi,Li Jie,Jiang Shengju,et al.Unsteady viscous flow simulations with deforming grid[J].Journal of Projectiles,Rockets,Missiles and Guidance,2005,25(3):186-188.

[6]冯文梁,李 杰,张 威.基于变形网格技术的翼型结冰数值模拟研究[J].西北工业大学学报,2008,26(5):550-555. Feng Wenliang,Li Jie,Zhang Wei.Exploring numerical simulation of icing flow-field of airfoil based on grid deformation technique[J].Journal of Northwestern Polytechnical University,2008,26(5):550-555.

[7]张来平,段旭鹏,常兴华,等.基于Delaunay背景网格插值和局部网格重构的变形体动态混合网格生成技术[J].空气动力学学报,2009,27(1):32-39. Zhang Laiping,Duan Xupeng,Chang Xinghua,et al.A hybrid dynamic grid generation technique for morphing bodies based on Delaunay graph and local remeshing[J].ACTA Aerodynamica Sinica,2009,27(1):32-39.

[8]Hardy R L.Theory and applications of the multiquadric-biharmonic method[J].Comput Math Applic,1990,19:163-208.

[9]李 艳,白玉峰.Multi-Quadric函数与Gauss函数的插值比较[J].内蒙古民族大学学报（自然科学版）,2010(4):369-372. Li Yan,Bai Yufeng.The case study about multi-quadric method[J].Journal of Inner Mongolia University for Nationalities, 2010(4):369-372.

Application of deforming mesh based on MQ interpolation in the ship resistance calculation

SHAO Fei,YANG Dong-mei,LIU Zhi-hao,LI Chuang-lan
(College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China)

A mesh deformation technique based on multi-quadric interpolation is developed in the framework of unstructured trim mesh.To apply this method to the resistance calculation of a Wave Piercing Catamaran with appendage,the CFD software STAR-CCM is used by coupling the SST turbulence model and the free surface profile is tracked by VOF method.The stretching deformation and slope deformation are used to implement the boundary motions of interceptor and stern wedge,respectively.Cases with the interceptor height of 4 mm,6 mm,8 mm and stern wedge angles of 5°,10°,15°are calculated.The numerical results show that the mesh deformation method has the same degree of accuracy comparing with the mesh fixation method.Validation of this method is carried out by comparison with the experimental results;the maximum average error is about 6.67%.Comparison of time consumption shows that the mesh deformation methods get a maximum computational time reduction of 40%to the mesh fixation method.Thereby,Using this method to predict the resistance of ships with appendage can greatly increase the computation efficiency.

multi-quadric interpolation;mesh deformation;interceptor;stern wedge;computational time consumption

O35

：Adoi:10.3969/j.issn.1007-7294.2016.04.009

1007-7294（2016）04-0452-08

2016-03-17

国家自然科学基金资助（51509053）

邵 菲（1987-），女，博士研究生；杨东梅（1979-），女，博士，通讯作者，E-mail:yangdm411@126.com。