环口板加强T形管节点抗冲击性能机理研究

李安令，曲 慧，霍静思

（1烟台大学土木工程学院，山东烟台264005；2湖南大学土木工程学院，长沙410082；3华侨大学土木工程学院，福建厦门361021）

环口板加强T形管节点抗冲击性能机理研究

李安令1，2，曲 慧1，霍静思3

（1烟台大学土木工程学院，山东烟台264005；2湖南大学土木工程学院，长沙410082；3华侨大学土木工程学院，福建厦门361021）

为深入研究环口板加强后T形管节点的抗冲击性能，文章采用试验研究和有限元研究相结合的方法，对未加强和环口板加强T形管节点的抗冲击性能进行了比较研究，旨在确定环口板加强节点受冲击后的典型破坏模态；并通过对变形发展、局部变形和整体变形的区分、冲击力-位移关系曲线、能量耗散等分析，揭示环口板加强节点的抗冲击工作机理，研究环口板的局部加强作用，确定环口板加强方式的有效性，可为管结构抗冲击设计和加固维护提供参考。

环口板加强T形管节点；冲击；变形区分；能量耗散；抗冲击机理

0 引 言

钢管结构凭借其独特的连接形式，易于呈现新颖、优美的建筑效果，在体育场、火车站、飞机场、工业厂房、海洋平台等结构中得到了广泛的运用。在服役期间，管结构不可避免地会遭受来自高空坠物、车辆、船舶等重物的低速碰撞。碰撞一般会造成受撞区域的局部屈曲，甚至构件的弯折破坏[1]，进而可能引起管结构整体破坏甚至倒塌，造成重大的生命、财产损失。由于管结构支管轴向刚度远大于主管的径向刚度，所以主管相贯线部位的节点区域是整个结构的薄弱部位，工程实践中，一般通过对节点进行加强来提高管结构的承载力。因此，选取合理的加强方法，对其进行抗冲击性能研究，具有十分重要的理论和工程意义。

管节点的加强方式主要有垫板加强、内置加筋环加强、内置插板加强、外置肋板加强、局部管壁加厚加强、环口板加强等方式[2]。但是大部分加强方式仅适用于设计阶段，而环口板加强方式不仅适用于设计阶段，还适用于服役期间承载力不足的管节点[3]。目前，国内外学者有关加强管节点的研究主要集中在静力承载力、应力集中系数、滞回性能等方面，而在抗冲击性能方面的研究鲜有报道。文献[2-9]研究表明适当的加强方式可以提高管节点的静力承载能力、改善管节点的滞回性能、降低焊接处的应力集中系数等。曲慧等[10-14]在湖南大学综合防护实验室已经完成了4个普通管节点和2个环口板加强管节点的落锤冲击试验，并对遭受横向冲击荷载作用下节点的破坏模态、冲击力、变形、能量耗散等抗冲击工作机理进行了深入的研究。

本文基于试验模型，建立ABAQUS有限元模型，并比较试验数据，验证有限元模型的有效性，在此基础上，对环口板加强的T形管节点进行抗冲击性能研究，研究环口板的局部加强作用，确定环口板加强方式的有效性，为管结构抗冲击设计和加固维护提供参考。

1 有限元分析模型

1.1 几何模型

图1 节点示意图Fig.1 Details of tubular T-joint

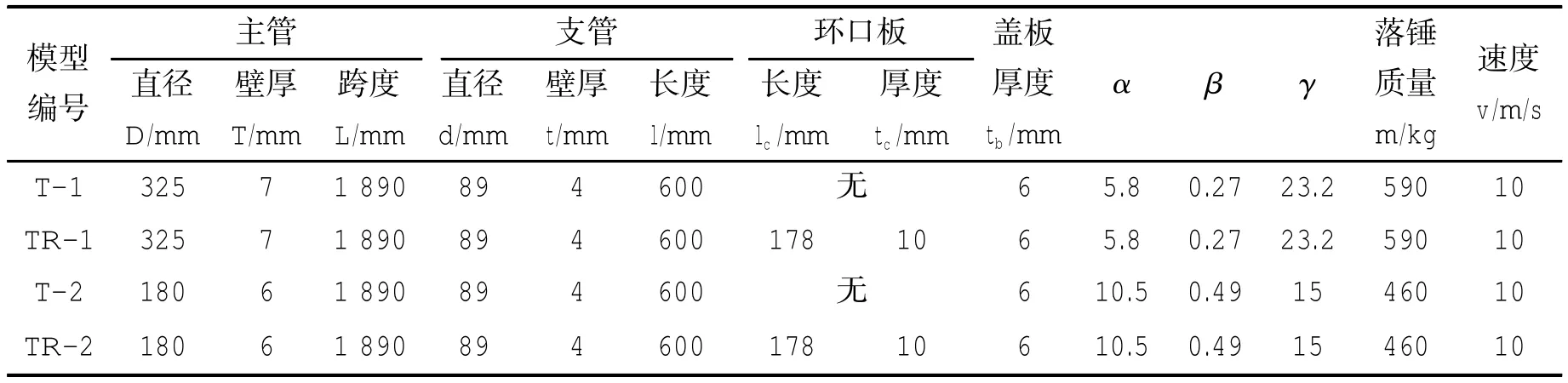
表1 管节点一览表[11]Tab.1 Summary of tubular T-joint information[11]

为方便验证有限元模型，节点尺寸参考曲慧等[11]文中相关尺寸取值，几何构造如图1所示，具体的几何参数如表1所示。表中，“T”系列节点模型为未加强节点，“TR”系列节点模型为环口板加强节点；D、T、L分别表示主管的外径、管壁厚度和长度；d、t、l分别表示支管的外径、管壁厚度和长度；lc和tc分别表示环口板的长度和厚度；α为主管长径比（α=L/D）；β为支主管直径之比（β=d/D）；γ代表主管径厚比（γ=D/ 2T）。

1.2 材料模型

钢材是典型的应变速率相关材料，Soares和Soreide[15]根据钢材在不同应变速率下的应力-应变关系曲线得出：应变速率的变化显著影响钢材的屈服强度，而对其极限强度、弹性模量影响较小。因此，国内外学者通过建立动态屈服强度增大系数表达式来考虑钢材的应变率效应。

Symonds[16]提出了钢材的动态强度增大系数表达式，该表达式能够利用依赖于应变率的参数来确定屈服应力，其动态屈服函数为：

其中：σdy为动态屈服强度，σy为静态屈服强度，为钢材的应变率，D、n为Cowper-Symonds模型的应变率参数。

ABAQUS有限元软件提供了三种应变率模型：屈服率模型、Johnson和Cook（J-C）模型，以及幂次模型（Cowper-Symonds模型）。其中，Cowper-Symonds模型形式简单，为众多学者所接受。

本模型中钢材材料模型为附加Cowper-Symonds应变率模型的理想弹塑性本构关系，其中钢材的材料参数取值采用材性试验所测得的数据，应变率参数参考文献[16]取值，如表2所示。

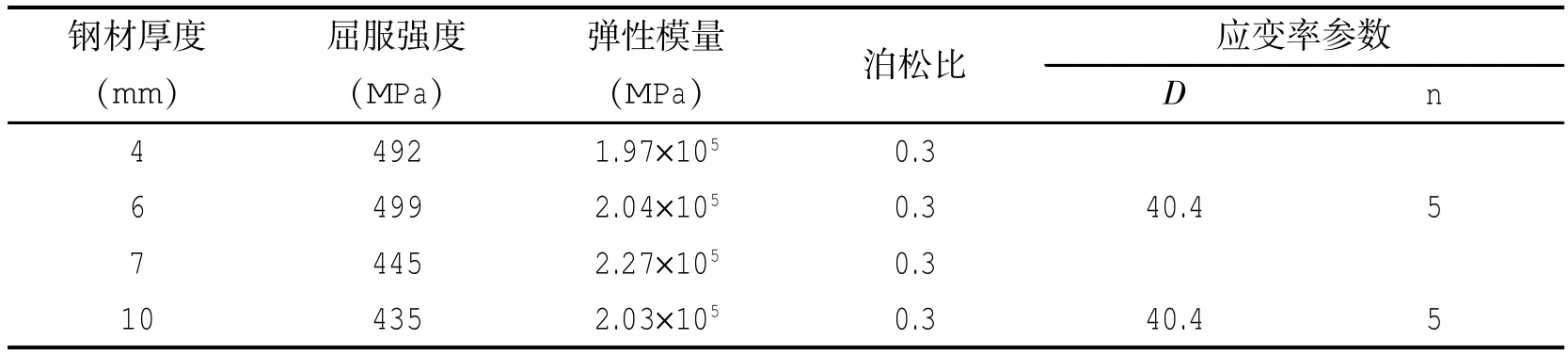
表2 钢材力学性能Tab.2 Material properties of steel

试验中，锤体由配重、冲击锤等组成，较为复杂，为简化模型，有限元模型中，不同质量的锤体用一个与支管直径相同、高度为100mm的圆柱体替代，通过改变其密度控制锤体质量。锤体为高强钢材制作而成，且试验时基本上处于弹性阶段，模型中通过增大弹性模量，缺省屈服强度，把锤体变形控制在弹性阶段。

1.3 边界条件、荷载、接触定义及网格

本文基于ABAQUS软件平台建立横向冲击下环口板加强圆钢管节点的有限元计算模型。由于冲击为瞬时动力学过程，采用软件中的显式动力学模块ABAQUS/Explicit进行分析。

有限元模型采用三维实体建模，通过约束主管端板中线的自由度来模拟试验中所用铰接边界条件，具体约束如图2所示。

图2 环口板加强节点有限元分析模型Fig.2 FEA model of collar plate reinforced T-joint

模型中施加两种荷载：一是节点自身的重力场；二是落锤对节点施加的冲击荷载，其施加方法为：将落锤放置在构件正上方，其轴线与节点支管轴线重合，在场力中为其定义沿支管轴线方向的平动初速度。

模型中采用两种接触类型：绑定（Tie），通用接触（General Contact）。有限元模型对焊缝进行了简化，端板与节点之间的焊接，简化为相互接触面间的绑定（Tie）接触；为方便建模，环口板外边缘与主管的焊缝简化为条形状（如图2所示），把“焊缝”与主管之间的接触面进行绑定（Tie）来模拟焊接；支管与主管之间的坡口焊，采用合并（merge）模拟。环口板底面与主管的接触、锤体与支管端板的接触，采用通用接触，防止锤体侵入节点，切向选择“罚函数”，设置0.3的库伦摩擦系数，法向采用“硬接触”。

经过试算确定网格密度，并通过加密节点变形较大的主支管相贯区域，稀疏其他部分来控制网格数量，网格划分如图2所示。模型采用三维实体八节点减缩积分单元（C3D8R）计算，以节约计算机资源。

2 有限元分析结果

2.1 破坏模式

图3对环口板加强和未加强节点的有限元模拟结果和试验结果进行比较。从图中可以看出：各试件有限元模拟所得到的破坏模态与试验结果吻合较好。对于未加强试件T-1、T-2，试件节点相贯处主管表面发生较大的局部凹陷变形；以主管下表面为参考，试件T-1整体弯折变形不明显，试件T-2整体弯折变形明显。随着冲击能和β的增大，未加强节点的破坏模式由节点相贯处主管表面局部凹陷控制的局部屈曲破坏（如图3a所示），逐渐过渡到主管局部屈曲和整体弯折相耦合的破坏形式（如图3b所示）。对环口板加强试件TR-1、TR-2，由于环口板的存在，相贯线附近节点主管刚度明显提高，并形成一块刚域。在冲击荷载作用下，随着冲击能和β的增大，其破坏模式由主管上表面沿环口板边缘发生局部凹陷变形，并伴有节点侧壁鼓曲（如图3c），过渡到环口板整体下陷，主管在环口板两侧各形成塑性铰线，同时节点发生整体弯折变形（如图3d）。

图3 试验与有限元模拟结果对比Fig.3 Comparison between test and FEA results

图4给出了冲击结束后，环口板加强节点TR-1和未加强节点T-1支主管相贯区域的变形图。可以看出：未加强节点T-1的局部变形由节点相贯线向外扩展，而加强节点TR-1的局部变形多发生在主管被环口板覆盖的部位。由此可以得出：环口板减弱了冲击力对节点主管壁的冲剪作用，明显提高节点相贯线部位的刚度，从而改变了节点的破坏模态，改善了节点的抗冲击性能。

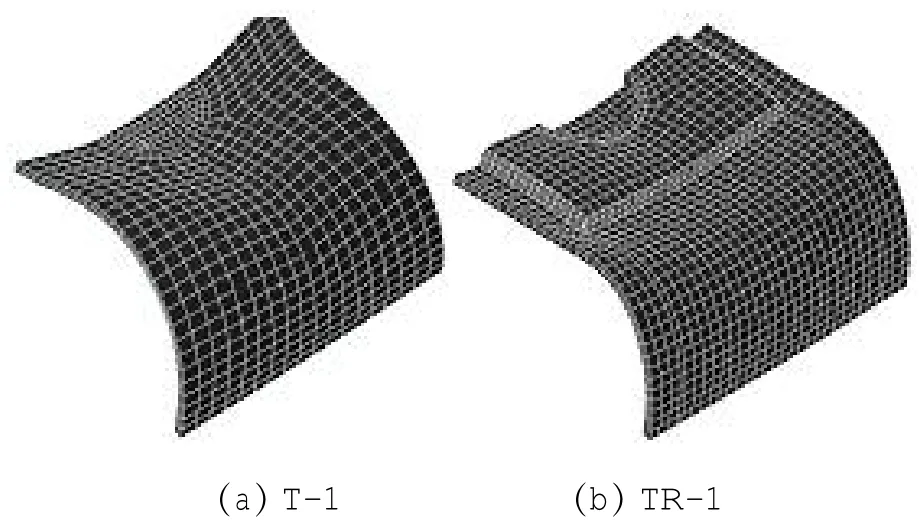
图4 节点局部变形图Fig.4 Deformation at the joint zone

2.2 节点的动力响应

为进一步验证本文所建立有限元模型的有效性，同时也比较环口板加强和未加强节点之间的性能差异，图5a和5b分别给出了节点的冲击力和位移时程曲线。试验过程中，由于试验设备故障，没能采集到试件T-2和TR-2的相关数据。所以，图5只列出了试件T-1和TR-1的试验和有限元模拟结果。

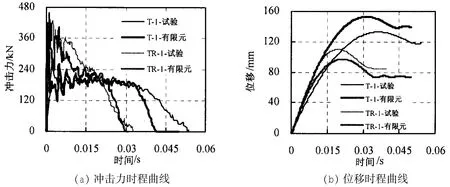
图5 加强和未加强节点的动力响应Fig.5 Dynamic response of reinforced and unreinforced joints

从图中可以看出，无论是冲击力时程曲线还是位移时程曲线，有限元结果和试验结果在曲线的发展趋势、峰值点、冲击时间等关键指标上基本一致，因此可以断定：本文所建立的有限元模型是可靠的，可以用来进行节点的抗冲击机理分析。

结合图3中试件T-1和TR-1的破坏模态与图5a中所给的冲击力时程曲线，可以看出：环口板可以显著增大节点相贯区域的刚度，在相对较低的同一冲击能量下，环口板加强节点的峰值承载力大幅度提高，相对于未加强节点约提高40%，下降段也有所提高，冲击时间明显变短。

从图5b中可以看出：在相同的冲击能量下，环口板加强节点和未加强节点支管顶部的变形发展趋势基本一致，均为抛物线形状。未加强节点支管顶部的变形值要较大于环口板加强节点支管顶部的变形值，大约为其的1.57倍。通过比较节点破坏模态、冲击力、位移时程曲线等，可以发现有限元模拟结果与试验结果吻合较好，从而验证了有限元模型的准确性。

3 环口板加强节点抗冲击机理分析

3.1 加强节点变形发展分析

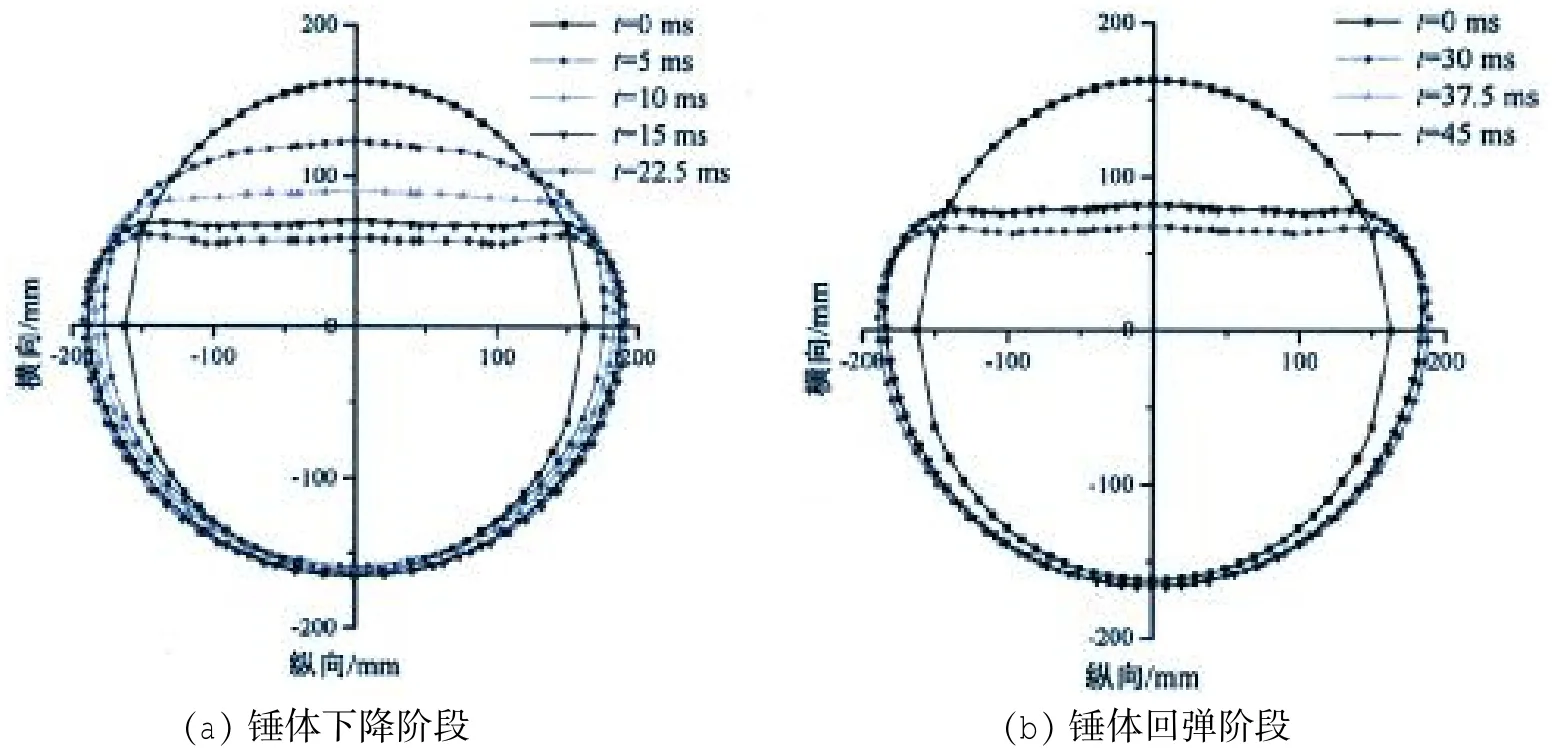
图6 节点TR-1主管跨中截面变形发展Fig.6 Deformation development of cross section at mid-span for joint TR-1

图6给出了环口板加强节点TR-1主管跨中横截面变形时程图。由于环口板下表面与主管紧密贴合，且边缘与支、主管焊接在一起，所以，冲击过程中，环口板与节点能够共同工作，协调变形。从图6a中可以看出，冲击开始后，环口板内边缘先产生变形，主管在冲击力和环口板挤压共同作用下发生较大的塑性变形。由于环口板的局部加强作用，相贯部位主管顶部凹陷量最大，环口板外边缘处，截面发生突变使刚度被削弱，导致凹陷较为明显。随着冲击能的传递，主管凹陷变形和侧壁鼓曲逐渐增大；冲击开始时，随着冲击波的传递，主管底部有上升趋势。从图6b中可以看出，随着锤体逐渐脱离支管，主管弹性变形逐渐恢复，直至锤体完全脱离结束。

3.2 加强节点变形区分

Johnson[17]认为在横向冲击荷载作用下，圆管的塑性变形可以分为三种形式：局部凹陷、整体弯曲以及两者之间的耦合。准确区分冲击过程中的局部变形和整体变形，将有助于确定节点的破坏次序。目前，一般通过测量节点特征点的位移来确定节点的变形。Choo等[3]在研究环口板加强管节点静力承载力时，定义节点冠点与主管跨中管底的位移差为节点的局部变形。Norman等（2010）[18]指出管受到横向冲击后的塑性变形主要由冲击部位的局部凹陷和管的整体弯曲变形构成。许超等[12]在研究管节点受横向冲击时的变形机理时，发展了Norman等（2010）[18]提出的区分横向冲击下钢管整体变形和局部凹陷的方法，认为在冲击荷载作用下当支管处于小变形状态，则可以不考虑支管变形，作者认为可以用变形前后主管跨中横截面上下两部分的等面积轴的移动来区分节点的整体变形和局部变形。

图7给出了用文献[3]和等面积轴法两种方法得出的节点TR-1的局部变形时程曲线。对于最终位移，文献[3]方法比等面积轴方法大出约15 mm，两者位移最大值相差更多。对于空心构件，研究其整体变形时，应该考虑构件的变形特征，应该把截面形心的移动作为参考，若只参考某外表面点的位移，所得结果是不准确的。因为在受撞过程中，节点相贯线附近发生大变形，而主管管底变形较小，所以，等面积轴方法所求得的局部变形更为准确。

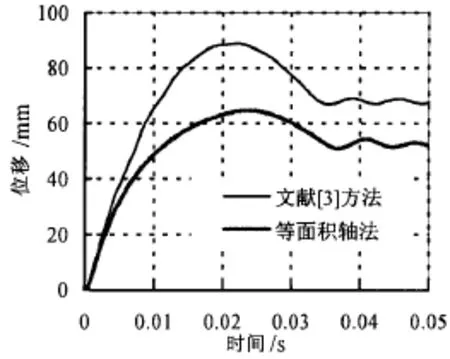
图7 TR-1节点局部变形时程曲线Fig.7 Local deformation vs.time history curves of joints TR-1

考虑到等面积轴方法较为准确，下文中节点变形均依据此法进行区分，区分后的整体变形用U表示，局部变形用δ表示。

图8给出了节点TR-1和点T-1局部变形和整体变形百分比时程曲线。根据管节点极限强度准则（Lu准则[19]）和梁极限挠度准则分别找到3%D和L/70对应的时间点，判断出构件破坏次序。从图8a可以看出，当遭受相对较小的相同冲击能时，节点TR-1和T-1先发生局部变形失效，且失效时间基本相同，之后节点T-1发生整体弯曲破坏。由于环口板的局部加强作用，节点TR-1在整个冲击过程中未发生整体破坏。从图8可以看出，当遭受相对较大的相同冲击能时，节点T-2先发生局部屈曲破坏，然后再发生整体弯曲破坏；但对于节点TR-2，由于环口板将塑性铰线外移，节点首先抗弯失效，在环口板边缘各形成一条塑性铰线，之后环口板整体下陷，节点局部失效破坏，但两者破坏间隔时间很短。

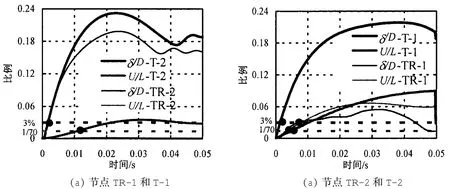
图8 节点整体和局部变形时程曲线Fig.8 Global and local deformation vs.time history curves of joints

从以上分析可以看出：（1）冲击能的大小和环口板的相对几何尺寸决定了加强节点的破坏模态。（2）冲击能相对较小且加强作用较弱时，节点先发生局部破坏，然后再发生整体破坏；冲击能相对较大且加强作用较强时，先发生整体弯曲破坏，然后再发生局部屈曲破坏。（3）采用环口板加强后的节点，其抗冲击变形能力明显提高。

3.3 冲击力-变形关系曲线

图9给出了环口板加强和未加强节点的荷载-位移关系曲线。从图9a可以看出，在相对较小的冲击能下，由于冲击过程中，节点TR-1和T-1主要表现为主管上表面局部凹陷，节点的整体抗弯刚度损失较小，曲线是相对较为饱满的；当节点遭受相对较大的冲击能时，节点TR-2和T-2的整体弯曲破坏占有较大比重，节点的整体抗弯刚度损失较大，因此，图9b中两个节点的曲线在达到峰值荷载后，出现了比较陡峭的下降段。

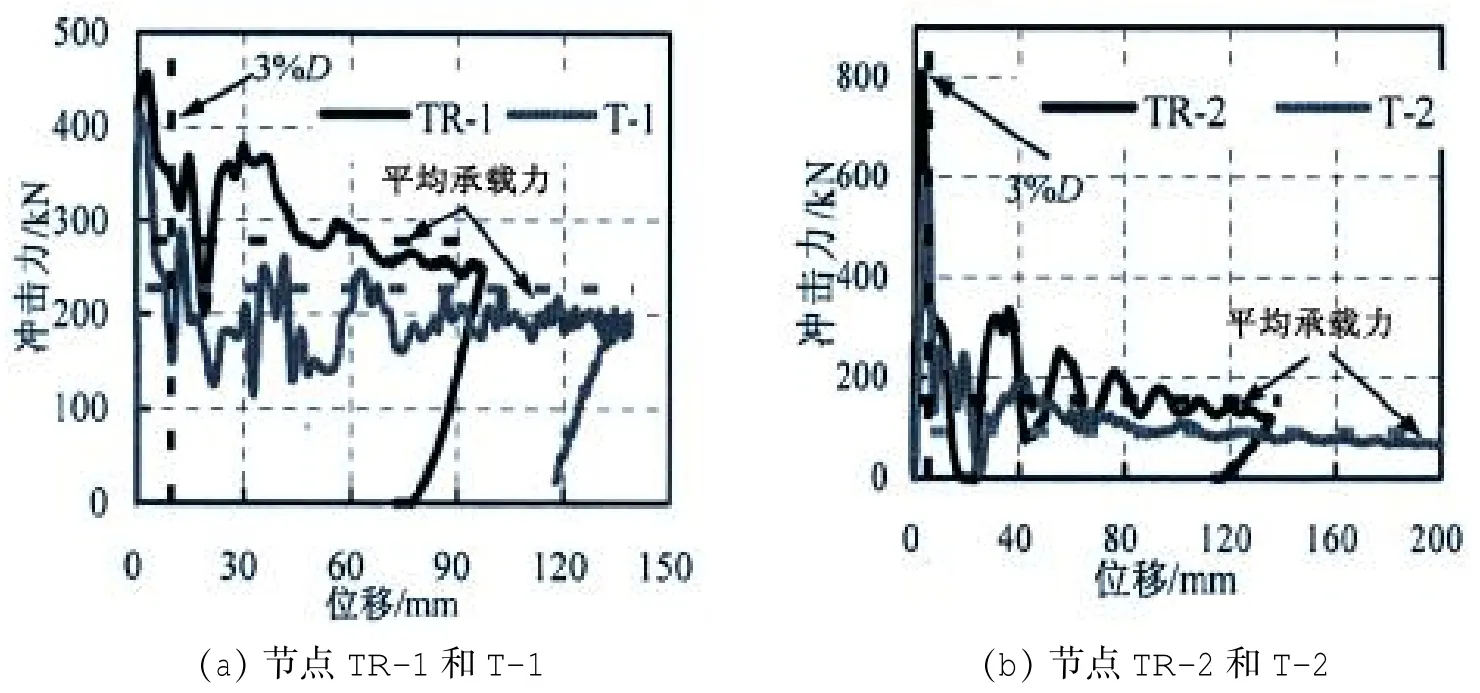
图9 冲击力-位移关系曲线Fig.9 Impact force versus displacement curves

目前，环口板加强圆钢管节点承载力方面的研究多集中在静力方面。一种方法是，如果节点的荷载-变形曲线有明显的下降段，则将节点的荷载-变形曲线的最高点所对应的荷载值作为其极限承载力；另一种方法是Lu[19]准则，通过限定管节点的局部变形来评估当支管轴向受载时节点的极限承载力。分析图9中所给出的冲击力-荷载关系曲线，虽然曲线存在明显下降段，但是峰值点前后曲线振荡较大，且3%D变形所对应的冲击力值基本位于剧烈的振荡段，所以，峰值法与Lu准则均不适合作为节点的冲击承载力的判定准则。

Wang等[20]研究预加轴力的钢管混凝土构件横向冲击性能时，对冲击力时程曲线进行三个阶段的划分，并把第二个阶段冲击力的平均值作为构件的稳定承载力。从图9可以看出：节点的冲击力-位移曲线也可以简化为线性上升、振荡下降和卸载回弹三个阶段。管节点在受到冲击后，短时间内，冲击力达到峰值；然后，进入塑性发展耗能阶段；此后，冲击卸载，节点弹性变形恢复。第二阶段是节点主要的耗能阶段，最能反映节点的抗冲击性能，本文将此阶段冲击力的平均值作为节点的抗冲击平均承载力，并以此判断节点的抗冲击能力，本文模型的平均承载力已在图9中画出，并列于表3中。

表3 节点的平均承载力Tab.3 Average bearing capacity of joints

从表3中可以看出，环口板加强后的节点的承载力较未加强节点明显提高。其中，节点TR-1较T-1提高22.6%，节点TR-2较T-2提高71.9%。所以，环口板加强措施能够有效提高节点的抗冲击性能。

3.4 能量耗散分析

图10给出了各节点整体变形和局部变形耗能时程曲线。从图中可以看出：（1）在相同的相对较小的冲击能下，节点TR-1（图10a）局部变形耗散了大部分能量，且节点局部变形耗散能量早于整体变形耗散能量，两者持续时间大体相同。与相同几何尺寸的未加强节点T-1（图10b）相比，经过环口板加强后，节点变形所耗散的总能量增大，且局部耗散的能量所占的比例相对增大。（2）当遭遇相对较大的冲击能时，环口板在主管和支管相贯的区域形成一个刚域，加强节点（TR-2）首先在环口板边缘发生整体弯曲变形，因此从图10c可以看出，节点首先由整体变形耗散能量。与图10d所示未加强节点T-2相比，节点耗散的总能量略微增加，但局部变形耗散能量较小。这说明：加强后的节点，使得塑性铰外移，节点区域基本没有破坏，破坏主要发生在节点域以外的主管上。（3）所有节点局部变形耗能达到其峰值后，弹性回弹相对较小。

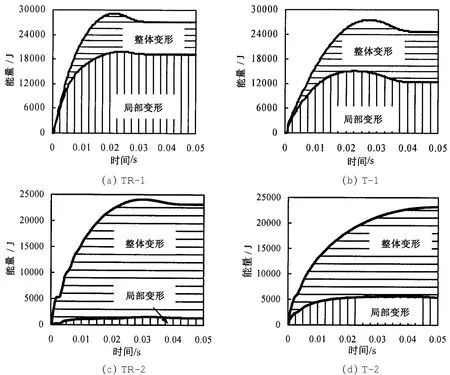
图10 能量耗散时程曲线Fig.10 Dissipated energy vs.time history curves of joints

4 结 论

本文采用试验和有限元相结合的方法，对环口板加强T形管节点进行了抗冲击性能工作机理分析。通过与未加强节点的比较，确定了节点的破坏模态；区分了冲击过程中的局部变形和整体变形；分析了能量耗散规律，得到以下几点结论：

（1）环口板加强方式，可以有效地提高节点的抗冲击性能；环口板加强节点在冲击荷载作用下，其破坏模态表现为节点相贯区域主管表面局部凹陷破坏，或表现为绕环口板边缘发生整体弯曲破坏；

（2）当遭遇的冲击能相对较小时，环口板可以减少节点域的局部凹陷量；当遭遇的冲击能相对较大时，环口板可以将节点的塑性铰外移，使得节点区域损伤较少；

（3）当相对冲击能较小时，环口板加强节点局部凹陷相对整体弯曲变形消耗大部分能量，局部变形早于整体变形；当相对冲击能较大时，环口板加强节点整体弯曲变形消耗大部分能量，整体变形早于局部变形；局部变形耗能达到其峰值后，弹性回弹相对较小。

参考文献：

[1]Bambach M R.Design of hollow and concrete filled steel and stainless steel tubular columns for transverse impact loads[J]. Thin-Walled Structures,2011,49(10):1251-1260.

[2]Shao Y B.Study on reinforcing methods for welded tubular joints structures[J].Journal of Yantai University(Natural Science and Engineering Edition),2009,22(4):312-320.

[3]Choo Y S,Liang J X,van der Vegte G J,et al.Static strength of collar plate reinforced CHS X-joints loaded by in-plane bending[J].Journal of Constructional Steel Research,2004,60(12):1745-1760.

[4]Choo Y S,van der Vegte G J,Zettlemoyer N,et al.Static strength of T-Joints reinforced with doubler or collar plates.I:experimental investigations[J].Journal of Structural Engineering,2005,131(1):119-128.

[5]Shao Y B,Li T,Lie S T,et al.Hysteretic behaviour of square tubular T-joints with chord reinforcement under axial cyclic loading[J].Journal of Constructional Steel Research,2011,67(1):140-149.

[6]蔡艳青,邵永波.环口板加固T型圆钢管节点的应力集中系数[J].土木工程与管理学报,2011,28(2):26-31. Cai yanqing,Shao yongbo.Stress concentration factor for circular tubular T-joints with collar plate reinforcement[J].Journal of Civil Engineering and Management,2011,28(2):26-31.

[7]吴亮秦,李自林,韩庆华.垫板加强N型圆钢管相贯节点静力性能试验研究[J].建筑结构学报,2010,31(10):83-88. Wu Liangqin,Li Zilin,Han Qinghua.Experimental study on static behavior of plate reinforced tubular N-joints[J].Journal of Building Structures,2010,31(10):83-88.

[8]李 涛,邵永波,张季超.内置竖向插板加强型管节点静力强度研究[J].工程力学,2010,27(4):133-140. Li Tao,Shao Yongbo,Zhang Jichao.Study of static strength of tubular joints reinforced with vertical inner plate[J].Engineering Mechanics,2010,27(4):133-140.

[9]Yang J,Shao Y B,Chen Cheng.Static strength of chord reinforced tubular Y-joints under axial loading[J].Marine Structures,2012,29(1),226-245.

[10]曲 慧,霍静思,许 超.T形管节点落锤动态抗冲击性能试验研究[J].建筑结构学报,2013,34(4):65-73. Qu Hui,Huo Jingsi,Xu Chao.Experimental study on tubular T-joints under drop hammer impact loads[J].Journal of Building Structures,2013,34(4):65-73.

[11]曲 慧,霍静思,许 超.环口板加强后T型管节点落锤抗冲击试验研究[J].振动与冲击,2013,32(1):108-112. Qu Hui,Huo Jingsi,Xu Chao.Experimental study on dynamic behaviors of collar plate reinforced tubular T-joints under drop weight impact loads[J].Journal of Vibration and Shock,2013,32(1):108-112.

[12]许 超,曲 慧,周新刚.冲击荷载作用下T型管节点变形初步分析[J].烟台大学学报（自然科学与工程版）,2012,25 (2):140-145. Xu Chao,Qu Hui,Zhou Xingang.Primary deformation analysis of T tubular joints subjected to impact load[J].Journal of Yantai University(Natural Science and Engineering Edition),2012,25(2):140-145.

[13]曲 慧,褚 飞.主管受撞T型管节点抗冲击性能研究[J].船舶力学,2011,15(11):1306-1314. Qu Hui,Chu Fei.Impact performance studies of T-tubular joint impacted on the chord[J].Journal of Ship Mechanics, 2011,15(11):1306-1314.

[14]曲 慧,张 云,邵永波.T型管节点抗冲击性能工作机理分析[J].船海工程,2010,39(4):161-164. Qu Hui,Zhang Yun,Shao Yongbo.Mechanism analysis of impact performance for tubular T-Joint[J].Ship and Ocean Engineering,2010,39(4):161-164.

[15]Soares C G,Soreide T H.Plastic analysis of laterally loaded circular tubes[J].Journal of Structural Engineering,1983,109 (2):451-467.

[16]Symonds P S.Survey of methods of analysis for plastic deformation of structures under dynamic loading[R].Brown University,Division of Engineering Report,BU/NSRDC/1-67,1967.

[17]Johnson W,Reid S R.Metallic energy dissipating systems[J].Applied Mechanics Reviews,1978,31(3):277-288.

[18]Norman J,Birch R S.Low-velocity impact of pressurised pipelines[J].International Journal of Impact Engineering,2010, 37(2):207-219.

[19]Lu H L,Winkel G D,Yu Y,et al.Deformation limit for the ultimate strength of hollow section joints[C]//Proceedings of the Sixth International Symposium on Tubular Structures.Melbourne,Australia,1994:341-347.

[20]Wang R,Han L H,Hou C C.Behavior of concrete filled steel tubular(CFST)members under lateral impact:Experiment and FEA model[J].Journal of Constructional Steel Research,2013,80:188-201.

Mechanical mechanism study of collar plate reinforced tubular T-joint under impact loading

LI An-ling1,2,QU Hui1,HUO Jing-si3
(1 School of Civil Engineering,Yantai University,Yantai 264005,China;2 College of Civil Engineering,Hunan University, Changsha 410082,China;3 College of Civil Engineering,Huaqiao University,Xiamen 361021,China)

In order to study the impact behavior of collar plate reinforced tubular T-joint deeply,a combined experimental study and finite element analysis is used to compare the impact performance of collar plate reinforced and unreinforced tubular T-joints.The study aims to obtain the typical failure modes of collar plate reinforced and unreinforced tubular T-joints.The mechanical mechanism of collar plate reinforced tubular T-joint under impact loading is unveiled by investigating the deformation development,dividing the local and global deformation,and evaluating impact force versus deformation relationship and dissipated energy versus time history curve.The local reinforcement effect of collar plate is verified,which can provide some suggestions to choose relevant reinforced method for design and strengthen the building.

collar plate reinforced tubular T-joint;impact;division of deformation;dissipated energy; impact resistant mechanism

U661.4

：Adoi:10.3969/j.issn.1007-7294.2016.04.011

1007-7294（2016）04-0469-09

2015-12-27

国家青年科学基金项目（51478407）；高等学校博士学科点专项科研资助项目（20130161110018）；山东省政府资助出国留学项目

李安令（1988-），男，博士研究生，E-mail:onlinglee@gmail.com；曲 慧（1976-），女，博士，副教授，通信作者，E-mail:quhuiytu@gmail.com。