船舶尾部模态数值计算与测试

刘长卿，车驰东，闫 菲

（上海交通大学a.船舶海洋与建筑工程学院；b.海洋工程国家重点实验室，上海200240）

船舶尾部模态数值计算与测试

刘长卿a，b，车驰东a，b，闫 菲a，b

（上海交通大学a.船舶海洋与建筑工程学院；b.海洋工程国家重点实验室，上海200240）

为了提高船舶尾部模态计算的精度，文章提出了一种尾部详细结构与船体骨架结合的简化有限元模型，应用该模型对某全回转推进船舶尾部模态进行了计算，并将其结果与另外两种传统简化模型（即尾部三维模型与尾部+一维梁混合模型）的计算结果进行了比较。研究发现改进模型与传统模型在尾部局部模态计算中没有明显差别，但对整体模态而言其差异随频率增大而增大。为了进一步验证模型的有效性，在航行过程中对该船舶振动情况进行了测试，并利用运行模态分析法识别尾部整体模态。通过识别结果与计算结果的比较可见，三种模型在基频（1阶弯曲）计算时误差均很小，但是在高阶固有频率计算中改进的模型误差明显小于另两种模型。

船舶尾部模态；有限元；实船测试；运行模态分析

0 引 言

随着现代船舶对航行速度和推进力的要求越来越高，大规模主推进系统和辅助机械在船舶中的应用越来越多，这就导致了船舶结构剧烈振动问题大量浮现出来。由于高能量振动不仅影响动力机械的正常运转而且导致了结构疲劳损坏，所以越来越多的工程设计人员开始关注船舶减振与控制的研究。船舶尾部是船体振动问题最多的区域，一方面因为尾部存在密集的振源，比如各种辅助机械，另一方面是尾部的结构刚度相对于船体其它部分较小，尤其是对于全回转推进船舶，该类船舶由于推进方式的特殊性，导致尾部舱段截面大幅度变小，其尾部结构刚度相对于主船体有很大的突变，这就使得船舶尾部的振动问题格外突出。船体结构模态反映了船体结构振动的固有特性，其模态参数是由固有频率、模态振型和阻尼等参数组成，对船舶尾部模态进行研究有利于优化船体结构动力学特性，避免在结构设计中出现动力学缺陷。

近年来国内外对船舶结构振动问题有大量研究，主要研究方法包括解析法、数值法和实船测试法。解析法的运用以板、梁及其组合结构的振动特性研究为主，可用于分析船体局部板架结构的振动特性[1-2]，也可将整个船体简化为特定截面形式的梁模型，推导梁的振动特性[3-4]。对于简化后的船体板、梁等结构振动特性的研究，解析法能够给出准确的结果，但对于复杂船舶结构做详细的振动特性分析时，其复杂的数学方程难以求解。随着计算机技术的发展，以有限元法为主的数值方法越来越多地被应用于船舶结构振动特性分析，在船舶尾部舱段结构振动、整船模态分析和上层建筑振动等方面已有大量文献发表。金咸定等[5]针对某高速舰艇的主机换装，进行了艉部振动响应的预报，探讨了建模、模型的校正、以及阻尼和激振力的选取问题。邹春平等[6]用有限元技术对船舶进行模态分析以及振动响应数值计算，比较了接近真实的整船有限元模型和尾部结构三维模型与梁组合的混合有限元模型的计算结果，总结了不同模型的适用性。Lin等[7]建立了船体舱段有限元模型，分析了在不同的加载方式下船体结构振动响应情况，得到了船体结构振动控制的重要结论。殷玉梅等[8]对船舶上层建筑建立不同的有限元模型，计算了尾部上层建筑整体振动模态，讨论了不同建模方法的优缺点和适用性。有限元法在静态分析和低频动态分析方面能够得到较为精确的结果，但对于高频动态分析由于其对网格精度要求较高往往容易产生较大误差。近年来，得益于测试设备和信号处理技术的快速发展，实测研究方法逐渐成为研究船舶振动问题的重要手段[9-10]。实船测试以及简化实验被直接用于工程实际以及对理论分析和数值计算结果的验证。

本文以某全回转推进船舶为例利用有限元法对船舶尾部模态进行研究，建立了三种不同的有限元模型计算尾部模态，比较了不同的建模方法对尾部模态分析结果的影响，并通过实船测试和运行模态分析法得到了实船尾部模态参数，以验证不同模型的适用性，为船舶尾部振动的研究方法提供一定的参考。

1 随机子空间法模态识别原理

常用的模态分析方法包括实验模态分析（EMA）和运行模态分析（OMA）。实验模态分析法（即测力法）需要一个可测量的宽频激励力，以获取传递函数，该方法通常用于小的模型实验。对于实际工程中的诸如船舶结构等大型结构，很难提供一个已知的足够大的宽频激振力来保证结构振动的振幅和形变可测量。运行模态分析法（即不测力法）是只从振动响应信号中提取模态参数的一项技术，它并不需要测量激振力，能够在设备运行或其他一些无法测量激振力的情况下进行模态测试[11]。本文运用OMA法中的随机子空间法来识别船舶尾部模态。

1.1 基于参考点的随机状态空间模型

模态测试中，测试信号来自于很多不同的测点，其中一个或多个被选作参考点。假设某测量过程中有l个测点，其中前r个测点被选作参考点。系统输出向量如下：

定义Hankel块矩阵如下：

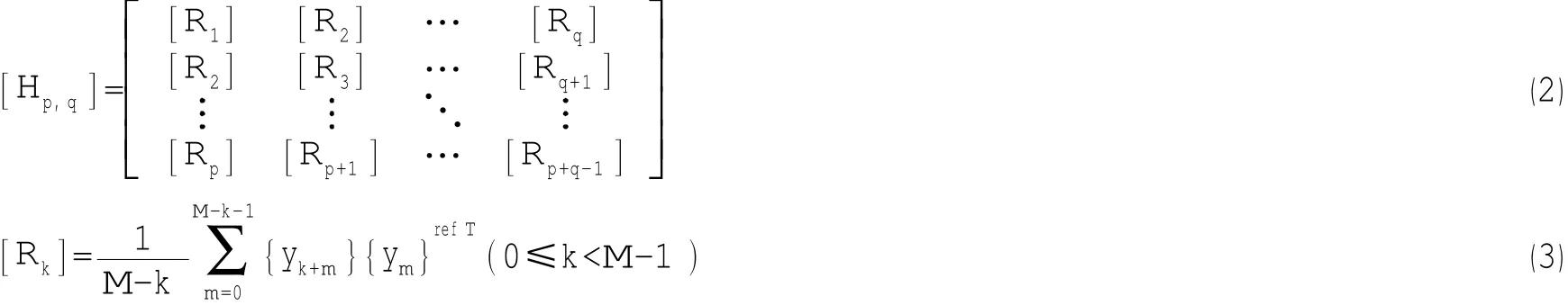
其中：［Rk］是两个响应点间的互相关序列。k是“过去”数据长度，即时间延迟，m为“将来”数据长度。定义上式的前提是假设“过去”数据中包含着足以预测“将来”的全部信息。

根据随机子空间识别理论，投影矩阵可以分解为观测矩阵和Kalman滤波状态序列的乘积：

其中：A∈Rn×n是系统状态矩阵，C∈Rl×n是输出矩阵，是“下一状态方差矩阵”。Hankel矩阵的奇异值分解如下：

其中：［Op-l］↑是［Op］去掉前l行的子矩阵，［Op-l］是［Op］去掉后l行的子矩阵，［Op］l是［Op］的前l行组成的子矩阵。

1.2 根据子空间模型确定结构模态参数

根据上面确定的系统状态矩阵A和输出矩阵C，结构模态参数可通过下面步骤识别：①系统状态矩阵的特征值分解

②确定结构振动固有频率和模态阻尼比

离散时间系统和连续时间系统特征值的关系如下：

其中：μi是连续时间系统的第i个特征值，Δt是采样时间间隔。

振动固有频率和阻尼比可通过下式确定：

其中：ωi为第i阶固有频率，ξi为第i阶模态阻尼比，j是虚数单位。

③计算结构模态振型

其中：C是系统输出矩阵，Ψ是系统特征矩阵。

2 有限元分析

2.1 结构模型

传统的用于计算船舶尾部模态的简化有限元模型主要有两种，一种是仅考虑尾部详细结构的三维模型，一种是尾部详细结构的三维模型与等值梁结合的混合模型。仅考虑尾部详细结构的三维模型用于尾部结构振动分析时，不同的边界条件对尾部结构振动特性影响较大，其边界条件很难确定，因此研究人员提出了尾部详细结构的三维模型与等值梁结合的混合模型。该混合模型相对于仅考虑尾部详细结构的三维模型能够更加准确地反应尾部整体结构振动特性，近年来得到了广泛应用，但是由于梁单元与实际的复杂船体结构特性存在较大差异，且梁单元与尾部三维结构模型连接方式较复杂，在扭转和高阶弯曲变形的振动模态分析时，往往难以模拟真实情况，而且等值梁单元截面特性很难得到准确的计算，使得该模型在尾部模态分析时存在一定的局限性。为了提高船舶尾部模态计算的精度，本文提出了一种尾部详细三维结构与船体骨架结合的改进的简化有限元模型，并以某全回转推进船舶为对象建立有限元模型分别计算船舶尾部的整体模态和局部模态。为了比较改进的模型与传统模型的差异性，用同尺度的网格建立上述两种传统的简化模型，重复上述模态计算，并将结果进行对比。

三种有限元模型如下：

①改进的模型（尾部+船体骨架混合有限元模型）

考虑到传统建模方式具有一定的局限性，而整船详细三维模型单元数量过大不利于计算，本文对船中首部结构进行适当的简化以减少单元数提高计算效率。由于实际船体结构在承受弯扭等变形时主要取决于梁和强筋等组成的骨架结构的刚度和强度[7]，因此，可将中首部船体板和部分加强筋去掉，仅保留由主船体梁和强肋骨组成的骨架结构，将船体板以及部分加强筋的等效刚度和质量等参数均摊到梁单元中，所建立的尾部结构三维模型和中首部船体骨架结构混合有限元模型如图1。

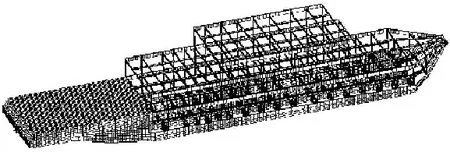
图1 改进的模型Fig.1 Improved model

②传统模型一（尾部结构三维模型）

由于全回转推进船舶舱段的截面面积在尾部大幅变小，从结构上看，尾部结构整体刚度要远小于主船体结构刚度，因此可将尾部与主船体连接处设为固定，对尾部三个舱段建立详细的三维结构有限元模型进行模态分析。该有限元模型包含外板以及去掉外板的模型示意图如图2所示，其中与主船体连接处的横舱壁设为固定。

在羊养殖产业发展中，羊巴氏杆菌病是一种十分常见的细菌性传染性疾病，临床上主要以败血症和肺炎为主要症状。羊巴氏杆菌病具有发病急、传播速度快、危害严重的特点，如果防控不及时，将会影响整个羊群的生长。由于羊年龄不同，患病羊所表现出的临床症状存在较大差异性，通常随着羊日龄的下降，临床症状呈现加重趋势，致死率更高。成年羊主要呈现一般性经过，发病时间较长，临床症状较为缓和。近年，随着市场对羊肉制品的需求量不断增加，羊养殖产业得到前所未有的发展，为确保养殖户经济效率，需要提高舍饲养羊的安全性和可靠性，保证羊群健康生长。

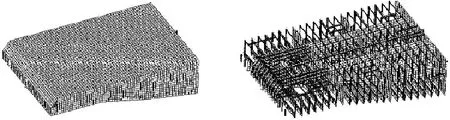
图2 传统模型一Fig.2 Traditional model 1

③传统模型二（尾部+等值梁混合有限元模型）

现有的船尾结构振动特性建模方法中，尾部详细三维结构与船中首部一维等值梁相结合的混合有限元模型应用较广泛。该方法将船中首部舱段简化为等值梁，各舱段的刚度和质量等结构参数经等效计算施加到梁单元上以模拟实际情况[5-6，12]。本文按该方法将船舶中首部舱段简化为一维等值梁模型，与尾部三维结构模型组成混合有限元模型，梁单元与尾部三维模型的交接处通过MPC连接，有限元模型如图3所示。

图3 传统模型二Fig.3 Traditional model 2

2.2 计算结果

用上述三种有限元模型进行模态计算，得到船舶尾部的整体模态和局部模态参数，分别如表1和表2所示。限于篇幅，本文仅给出三种结构模型的1阶纵弯和1阶扭转模态变形图，以及两种局部模态变形图，如图4～7。为了显示内部结构变形情况，各模态变形图中均隐藏了尾部甲板和舷侧外板。

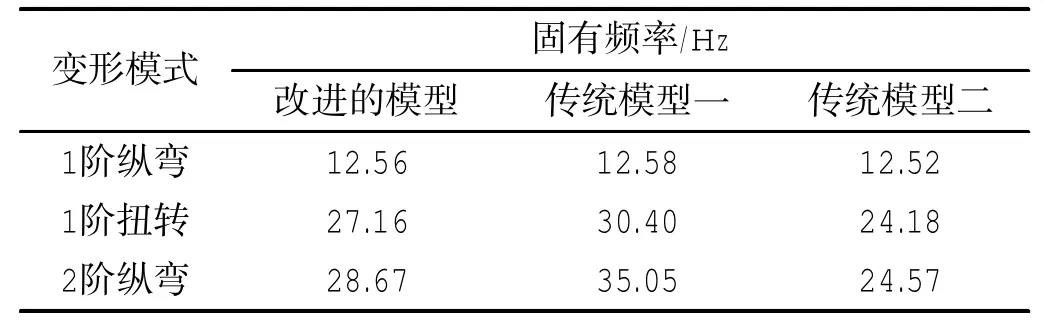
表1 船尾结构整体模态Tab.1 Whole structural modes of ship stern

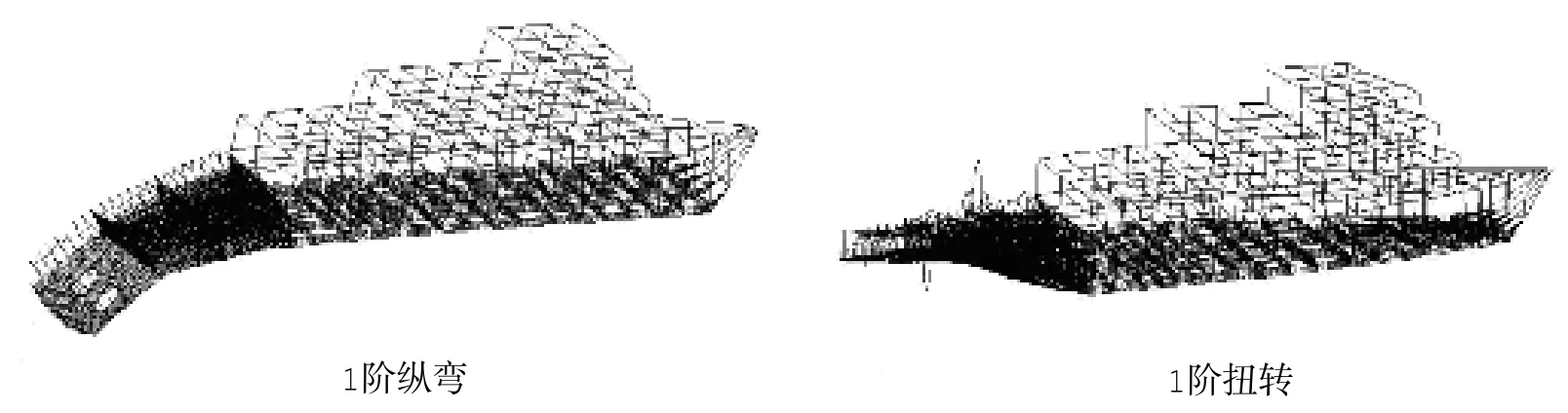
图4 改进模型的模态变形图Fig.4 Whole deformation of improved model

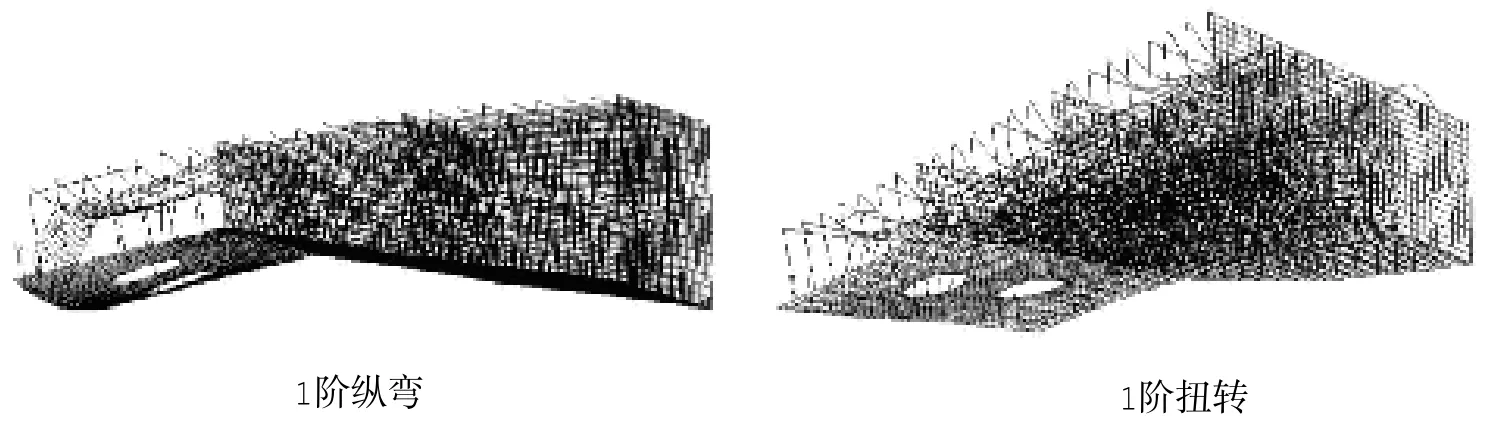
图5 传统模型一的整体模态变形图Fig.5 Whole deformation of traditional model 1

图6 传统模型二的整体模态变形图Fig.6 Whole deformation of traditional model 2

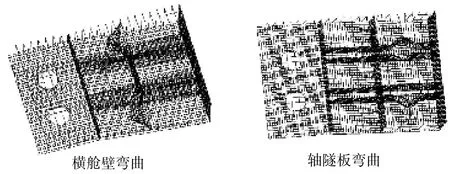
图7 局部模态变形图Fig.7 Local deformation

由模态计算结果可见：

①三种模型的尾部结构局部模态计算结果相近（局部变形均如图7），这说明尾部局部模态的计算受到整体结构差异影响可忽略，因此计算尾部模态时可以直接用尾部结构模型计算；

②1阶纵弯模态固有频率计算结果相差较小，这说明在低频范围内进行振动计算时，三种模型的差异影响较小，与文献[6]的研究结论相符；

③2阶纵弯和1阶扭转模态固有频率计算结果出现较大差别，其中传统模型一计算结果最大，这是因为尾部结构模型在舱壁处设为固定导致其整体刚度加大造成的，而船中首部简化成等值梁后，对尾部结构的约束相对较弱，且等值梁的等效截面存在刚度突变情况，易导致整体刚度偏小，故传统模型二计算结果最小，改进模型的计算结果介于两者之间；

④不同模型的模态固有频率对比表明，尾部船体局部模态受到模型整体结构的影响很小，整体模态在低频范围内不同模型的计算差异较小，24 Hz以上中高频计算结果差异较大。

3 实船测试

为了对比验证上述不同模型模态分析结果的适用性，对该船进行实船航行测试，并识别其振动模态。由于船舶结构庞大，很难提供可测量的宽频激振力，因此在模态测试分析中采用不测力法，即运行模态分析（OMA）。实船测试过程中，船舶连续直线航行，主机转速自1 150 rpm起，每隔5分钟增加50 rpm，直至1 750 rpm最高转速工况，以2.56 kHz采样频率连续采集各工况下船上重要位置的垂向振动响应信号，利用之前介绍的OMA法对其模态进行识别，并与三种模型计算结果作比较。

测试过程中共选取了15个测点，船尾甲板布置9个测点，船中首部沿主甲板中线布置5个测点，主机基座布置1个测点，测点布置示意图如图8所示。

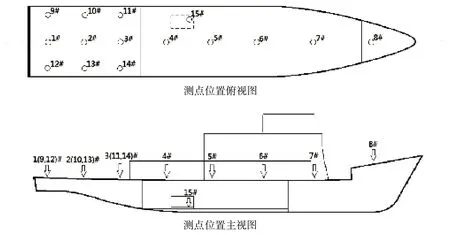
图8 测点布置示意图Fig.8 Location of measurement points

主机基座测点和部分甲板测点的时间波形对比如图9。由图9可见，主甲板尾部测点1的振动加速度远远超过中首部甲板测点5和测点8，且随着转速增大，测点1的振动逐渐超过主机基座测点15的振动，这说明尾部舱段存在较严重的振动问题。

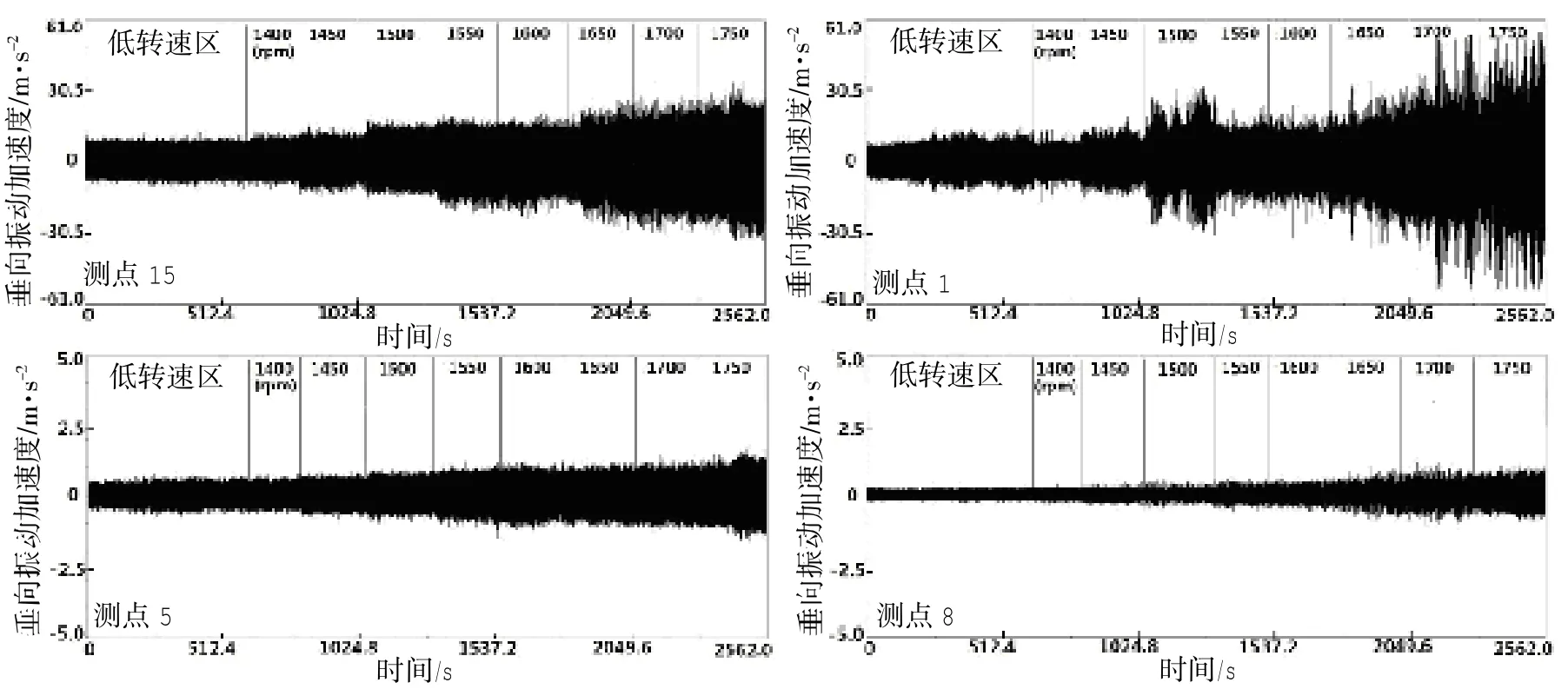
图9 主机基座与甲板部分测点时间波形图Fig.9 Time-domain waveform of several measurement points

利用随机子空间法识别该船舶的1阶纵弯、2阶纵弯和1阶扭转模态。模态分析结果如表3所示。

有限元计算结果相对于实船测试分析结果的误差如表4所示。由表4可见，改进模型的计算结果与实测分析结果更接近，1阶纵弯固有频率相对误差在1%以内，1阶扭转和2阶纵弯模态固有频率误差稍大，但在可接受范围内。而传统模型一和传统模型二的计算结果中，1阶扭转和2阶纵弯模态固有频率相对误差较大。

实船测试结果表明，上述三种有限元模型在进行尾部整体模态分析时，对于低频段的1阶纵弯模态分析均保持较高准确性，而对于24 Hz以上的1阶扭转模态和2阶纵弯模态的分析只有改进模型的精确度较高，其最大相对误差仅为4.67%。

表3 实船测试模态分析结果Tab.3 Results of OMA

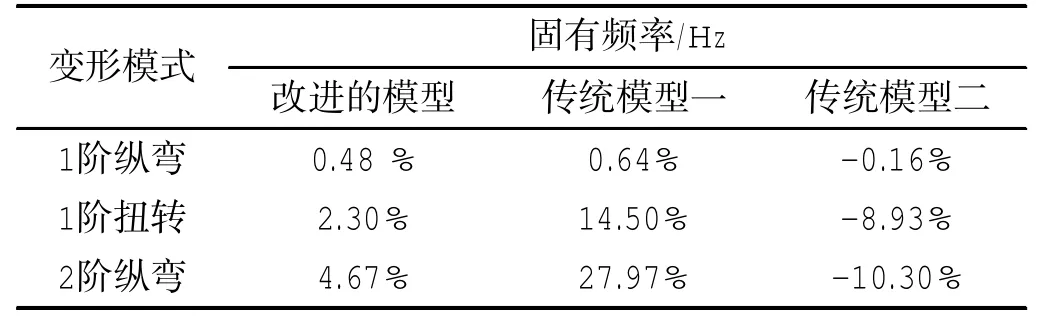
表4 有限元计算结果相对于实测分析的误差Tab.4 Relative errors between results of FEM and OMA

4 结 论

本文利用有限元法和实船测试相结合分析了船舶尾部振动模态。首先建立尾部三维模型、尾部+等值梁模型和尾部+船体框架模型三种不同的有限元模型，分别进行模态分析，得到尾部振动的整体模态和局部模态，然后进行实船振动测试并识别尾部振动的整体模态，通过不同模型的模态分析结果与实测结果的对比得到下列结论：

（1）三种结构模型的尾部结构局部模态计算结果几乎相等，整体结构模型差异对尾部局部模态造成的影响可忽略，研究尾部局部模态可直接通过尾部模型来分析；

（2）三种结构模型的1阶纵弯模态固有频率计算结果相差较小，且均与实船测试结果相近，这说明在低频范围内进行振动计算时，三种模型均能达到较高精确度；

（3）三种模型的2阶纵弯和1阶扭转模态固有频率计算结果与实测结果相比，两种传统模型模态计算结果相对误差较大，改进模型的计算结果与实测结果相差较小，这说明对于24Hz以上的中高频段模态计算改进模型的精确度最高。

[1]Lin T R,Pan J.A closed form solution for the dynamic response of finite ribbed plates[J].Acoustical Society of America, 2006,119(2):917-925.

[2]Lin T R.A study of modal characteristics and the control mechanism of finite periodic and irregular ribbed plates[J].A-coustical Society of America,2008,123(2):729-737.

[3]SenjanovicˊI,CˊatipovicˊI,TomaševicˊS.Coupled flexural and torsional vibrations of ship-like girders[J].Thin-Walled Structures,2007,45(12):1002-1021.

[4]SenjanovicˊI,CˊatipovicˊI,TomaševicˊS.Coupled horizontal and torsional vibrations of a flexible barge[J].Engineering Structures,2008,30(1):93-109.

[5]金咸定,傅敬华,胡常云.某高速舰艇主机改装的艉部振动响应预报[J].上海交通大学学报,1997,31(11):75-77. Jin Xianding,Fu Jinghua,Hu Changyun.Stern vibration response prediction of a high-speed craft due to change of the main engine[J].Journal of Shanghai Jiao Tong University,1997,31(11):75-77.

[6]邹春平,陈端石,华宏星.船舶结构振动特性研究[J].船舶力学,2003,7(2):102-115. Zou Chunping,Chen Duanshi,Hua Hongxing.Study on structural vibration characteristics of ship[J].Journal of Ship Mechanics,2003,7(2):102-115.

[7]Lin T R,Pan J,Peter J.O'Shea,Chris K.Mechefske.A study of vibration and vibration control of shipstructures[J].Marine Structures,2009,22(4):730-743.

[8]殷玉梅,赵德有.船舶上层建筑整体振动有限元建模方法研究[J].中国造船,2009,50(3):49-56. Yin Yumei,Zhao Deyou.Study on the FE modeling method of the ship superstructure's overall vibration[J].Shipbuilding of China,2009,50(3):49-56.

[9]Jiang Dazheng,Hong Ming,Zhou Li.Study on operational modal parameters identificationof ship structures[J].Journal of Ship Mechanics,2011,15(3):313-324.

[10]万 岭,洪 明.环境激励下船体模态参数识别实验研究[J].振动与冲击,2012,31(8):57-61. Wan Ling,Hong Ming.Modal parameter identification of a ship structure under ambient excitation[J].Journal of Vibration and Shock,2012,31(8):57-61.

[11]张义民,张守元,李 鹤,等.运行模态分析中固有模态和谐波模态区分方法研究[J].振动与冲击,2009,28(1):64-67. Zhang Yimin,Zhang Shouyuan,Li He,et al.Modes in operational modal analysis[J].Journal of Vibration and Shock, 2009,28(1):64-67.

[12]朱胜昌,郭 列,何富坚,等.大型自卸船振动性能预报研究[J].船舶力学,2000,4(2):27-43. Zhu Shengchang,Guo Lie,He Fujian,et al.A study on vibration characteristics prediction of a large self-unloading ship [J].Journal of Ship Mechanics,2000,4(2):27-43.

Modal analysis of ship stern by numerical and experimental method

LIU Chang-Qinga，b,CHE Chi-Donga，b,YAN Feia，b
(a.State Key Laboratory of Ocean Engineering;b.School of Naval Architecture,Ocean& Civil Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

To improve the accuracy in ship stern modal analysis,a 3D ship stern+ship hull frame simplified FE(finite element)model is put out and the stern mode of a full-revolving propulsion ship is calculated by using this FE model.The calculation results are compared with those of other two traditional simplified models(3D ship stern model and 3D ship stern+1D beam model).The comparison indicates that the improved model and the two traditional models show no significant difference in local modal calculation while in terms of whole modal calculation the difference increases with the increase of frequency.To further validate the FE model,a ship navigation testing is carried out and the whole structural modes of ship stern are identified through OMA(operational modal analysis)method.The comparison between results of FEM(finite element method)and OMA shows that the relative errors of whole structural modes in base frequency are all small while those of the improved model are relatively smaller than those of the two traditional models in high frequency.

ship stern modes;FEM;ship navigation testing;OMA

U661.44 TB533

：Adoi:10.3969/j.issn.1007-7294.2016.04.012

1007-7294（2016）04-0478-09

2015-06-30

国家自然科学基金资助项目（National Natural Science Foundation of China）（51109131）

刘长卿（1989-），男，硕士生；车驰东（1980-），男，讲师，硕士生导师，通讯作者，E-mail:churchdoor@sjtu.edu.cn。