基于变论域模糊控制的大型风电机组偏航系统

韩 兵， 周腊吾， 陈 浩， 田 猛， 邓宁峰

(1. 湖南大学, 湖南 长沙 410082; 2. 长沙理工大学, 湖南 长沙 410114; 3. 湖南世优电气股份有限公司, 湖南 湘潭 411101)

基于变论域模糊控制的大型风电机组偏航系统

韩 兵1， 周腊吾2， 陈 浩3， 田 猛1， 邓宁峰1

(1. 湖南大学, 湖南 长沙 410082; 2. 长沙理工大学, 湖南 长沙 410114; 3. 湖南世优电气股份有限公司, 湖南 湘潭 411101)

风力发电在解决能源和环境问题上的积极意义，使其成为增长速度最快的绿色能源之一。偏航控制是大型风力发电机组的热门研究课题，偏航系统是典型的非线性、时变系统，常存在较大程度的参数变化和大时变负载与干扰。本文提出一种变论域模糊偏航控制策略，将变论域模糊控制与风向标反馈控制相结合，将风向数据与功率数据进行迅速的对比识别处理，来实现变论域模糊控制参数自整定和控制规则的自调整，提高偏航控制系统对风速扰动和参数变化的适应能力，最后进行风电机组偏航控制的仿真与实验，证明变论域模糊偏航控制具有动态响应快、抗干扰能力和鲁棒性强等优点。

大型风电机组； 偏航系统； 变论域； 模糊控制

1 引言

风向变化会引起风力发电机组输出功率的脉动，随着电网中风电容量的增加，输出功率的脉动将会影响电网的稳定性[1]。偏航系统是风力发电机组特有的伺服系统，它的作用一是跟踪风向的变化，在可用风速范围内旋转风轮使风向与扫掠面始终处于垂直状态，保证风电机组最大捕获风能，而在非可用风速范围下能够保持90°侧风，以保证风机的稳定的停机状态；二是在连续跟踪风向可能造成电缆缠绕的情况下进行自解缆；三是当风轮保持迎风位置时，通过控制偏航电机及轴承提供相应的锁紧力矩，维持风机的安全运行[2-4]。

由于风机非线性的空气动力学特性、系统参数的不确定性，很难给出精确的数学模型，这给风机的控制带来许多困难[5-7]。为提高风机的功率利用系数，国内外学者相继提出了各种有效的控制策略，但主要是在风机的变桨距、发电机和并网控制等方面的研究，在偏航控制方面仍然未能取得有效的进展[8,9]。文献[10]中的偏航控制方法的对风精度均只达到了15°，显然此种偏航控制方法精确性不够。文献[11,12]中偏航控制方法采用传统的PID控制方法，其参数的选取对系统的控制品质有很大的影响。文献[13]提出模糊PID控制方法，将模糊控制与PID控制器相结合，但此种控制方法不能及时地调整自身的控制参数，表现出较差的自适应性。

本文利用智能控制理论，设计了一种基于变论域模糊偏航控制策略。首次将变论域模糊控制与风向标反馈控制相结合的偏航控制策略，即让风向数据或功率数据进行迅速的对比识别处理后，来实现模糊控制器的参数、隶属函数和控制规则的自整定，以提高控制系统对扰动和参数变化的鲁棒适应能力，然后根据系统参数的变化发出偏航命令，使偏航电机偏转到相应的位置以达到有效对风的目的。本文通过仿真和实验，验证了变论域模糊偏航控制策略的可行性和有效性。

2 风电机组系统特性

风能的基本转换过程即动能转换为电能，其风电机组的输出功率P与风速v的之间关系为：

(1)

(2)

式中，ρ为空气密度；R为风轮半径；ω为风轮角速度；β为桨距角；λ为叶尖速比；n为风轮转速；Cp为风能利用系数。

风能利用系数Cp是表征风力发电机组吸收转换风能程度的重要参数。风能利用系数Cp可以用式(3)近似表示，Cp-λ特性曲线如图1所示。

(3)

图1 风能利用率Cp-λ的关系图Fig.1 Wind energy utilization Cp-λ diagram

本文建立简化的大型风电机组模型的状态方程，如式(4)和式(5)所示：

(4)

(5)

式中，Ωr为风轮转速；J为风轮转动惯量；Mr为风轮转矩；S为风机塔基刚度；M为机舱总质量；snay为机舱左右扰度；H为机舱高度；D为风机的阻尼系数；Myaw为偏航力矩；Fsd为机舱的侧向力。

风电机组偏航原理是将风向传感器检测的风向信号送入偏航控制器，当发现风向与风轮轴线偏离一定角度时，偏航控制器就会根据风向信号，发出相应的偏航信号给偏航执行机构，调整风轮的方向，使风轮的扫掠面与风向保持垂直，实现风轮准确迎风[14]。偏航控制系统原理图如图2所示。

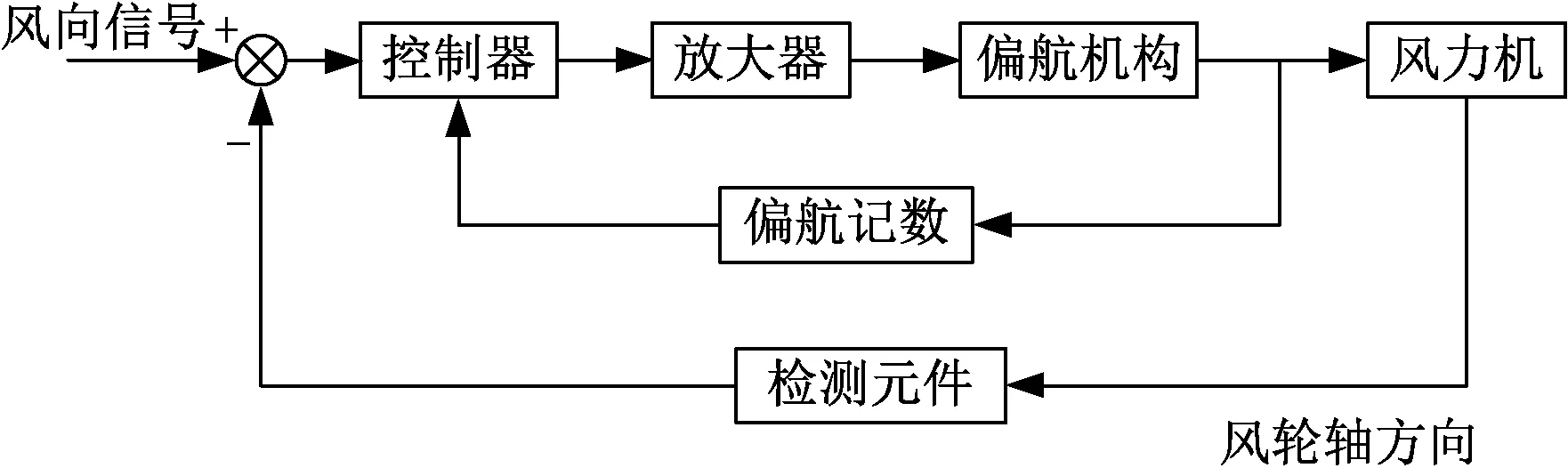
图2 偏航控制系统原理框图Fig.2 Block diagram of yaw control system

为实现风电机组的偏航控制，以水平轴进行分析，其风向角θW、风轮偏航角θe和风轮角度θT三者的关系有以下四种情况，其原理图如图3所示。

(1) 风轮法线方向与风向的差值为0°～90°时，风机选择锐角顺时针方向偏航，则偏航角θe为：

θe=θW

(6)

(2) 风轮法线方向与风向的差值为90°～180°时，风机选择钝角顺时针方向偏航，则偏航角θe为：

θe=θW

(7)

(3) 风轮法线方向与风向差值为180°～270°时，风机选择钝角逆时针方向偏航，则偏航角θe为：

(8)

(4) 风轮法线方向与风向差值为270°～360°时，风轮选择锐角逆时针方向偏航，则偏航角θe为：

(9)

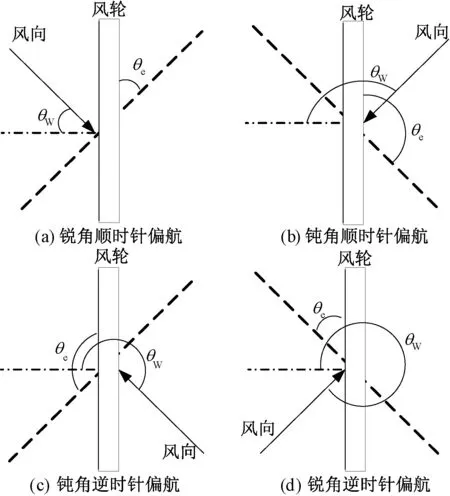
图3 风电机组的偏航角度原理图Fig.3 Yaw angle of wind turbine

3 变论域模糊偏航控制系统

由于风电机组的偏航系统是典型非线性时变系统，有较大的参数变化和大时变负载与干扰，因此建立精确的数学模型很困难。本文利用变论域模糊自调整偏航控制器采用模糊推理方法对参数进行在线调整[15]，以满足不同的风向对偏航控制参数的不同要求，设计的变论域模糊PID偏航控制器的结构如图4所示。考虑变论域模糊偏航控制系统的n输入单输出，令Xi=[-Ei,Ei](i=1,2，…,n)和Y=[-U,U]分别为输入变量xi(i=1,2,…,n)和输出变量y的论域[16]。

图4 变论域模糊PID偏航控制器框图Fig.4 Variable universe fuzzy PID controller for yaw

为了达到满意的偏航系统控制精度，定义输入变量xp(p=1,2)的基本论域为Xp=[-Ep,Ep]，Xp上的模糊划分为Ai={aij}(1≤j≤m，m=7)；输出变量yq(q=1,2,3)的基本论域为Yq=[-kq,kq]，将Yq上的模糊划分为Bi={bj}(1≤j≤m)，结合偏航系统的模糊推理规则，则

(10)

变论域调整是指变量Xi与Y可以分别随着xi与y的变化而进行自动改变，输入变量Xi的基本论域为X(x)=[-α(x)E,α(x)E]，输出变量Y的基本论域为Y(y)=[-β(y)K,β(y)K]，其中，α(x)与β(y)为论域的伸缩因子。则αi(xi)的计算方法为：

(11)

则变论域模糊偏航控制器的模糊推理规则的n元分片动态插值函数表示为：

y=βω

(12)

(13)

而偏航控制器是以误差E和误差变化率Ec作为输入，控制器的三个参数PID的修正ΔKp、ΔKi、ΔKd作为输出。取输入E、Ec和输出ΔKp、ΔKi、ΔKd模糊子集为{NB, NM, NS, ZO, PS, PM, PB}，子集中元素分别代表负大、负中、负小、零、正小、正中、正大。本文建立的输出变量的模糊偏航控制规则如表1所示。

伴随着风向发生改变，变论域模糊偏航控制器采集计算到偏航角度差超过允许误差的范围后，根据E(k)及Ec(k)调整变论域模糊控制器的量化因子，并进行相应的模糊推理得到输出量，通过偏航控制器发出偏航指令，驱动偏航电机旋转执行风轮对风的校正动作，使风轮迎风面实现准确对风。图5为变论域模糊偏航控制过程流程图。

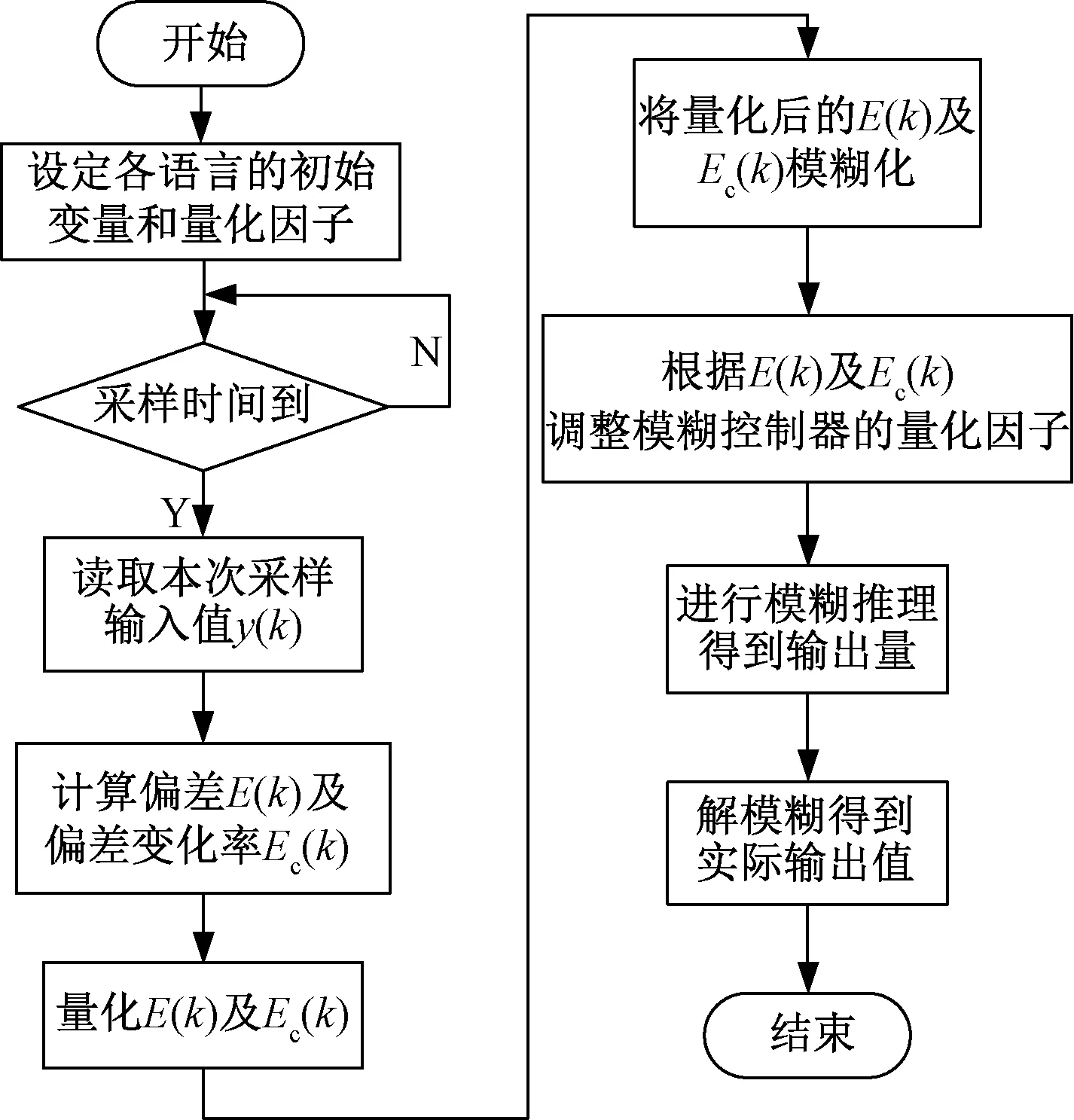
图5 变论域模糊控制流程图Fig.5 Variable universe fuzzy control flow chart

4 仿真与实验

为验证本文所提变论域模糊偏航控制系统的性能，本文在Matlab/Simulink建立仿真模型，对风电机组的偏航系统进行仿真，偏航系统的具体参数如表2所示。偏航电机设计误差大于100r/min时为正大，即E的基本论域为[-100,100]，Ec的基本论域为[-4×103，4×103]，由式(6)～式(8)可得KE=0.0025，KEc=1.25×10-4。初始参数取Kp0=5，Ki0=47，Kd0=2.5；Kp=15，Ki=2，Kd=0.02；KE1=18，KEc1=5。

偏航控制系统的对比仿真实验为本文设计的变论域模糊控制与模糊PID控制相比较，结果如图6所示。风向的变化经历±10°左右，如图6(a)所示。本文设计的变论域模糊控制与模糊PID控制表现出了不一样的控制特效，结果如图6(b)所示。变论域模糊控制系统风轮转速的波动也比模糊PID控制系统小，这是因为风电机组的非线性时变性无法给出精确的模型，模糊PID很难获得参数的全局最优值；而变论域模糊控制可以对不精确的非线性模型进行参数自整定。在20s时，风向急剧由-10°向+10°变化，变论域模糊控制器给定的偏航幅度和速度相对较小，进而有效地减轻偏航执行机构的磨损。变论域模糊控制器输出偏航角的变化率较小，却没有影响系统偏航电机的转矩，以适应风向的变化。在40s后，风向又出现+5°向-15°的变化趋势，由图6(c)可以看出，此时模糊PID控制时风轮波动较大，抑制转速波动幅值的效果不够理想，而基于变论域的模糊控制器能使转速快速稳定，平滑的偏航动作减小了输出功率幅值变化。

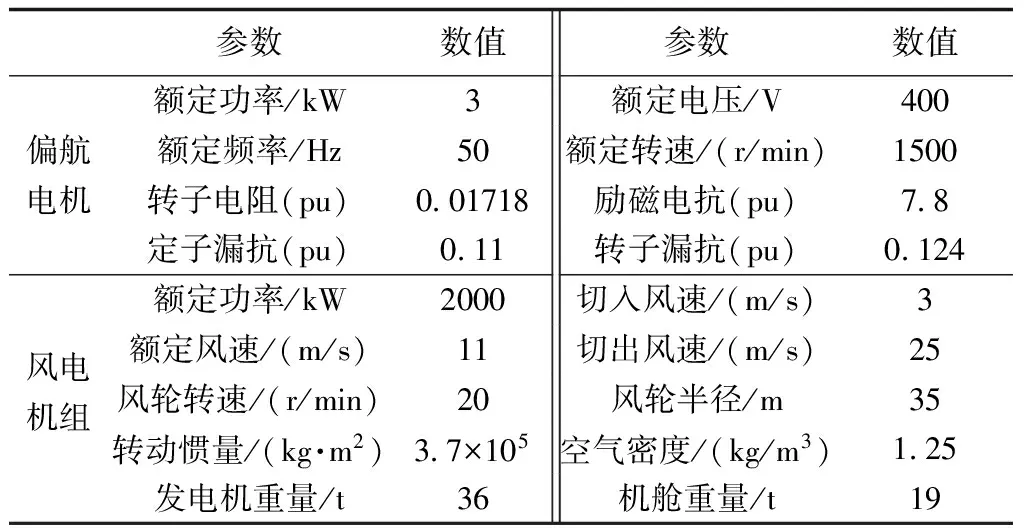
表2 偏航系统的具体参数表Tab.2 Parameters of yaw control system

图6 变论域模糊控制仿真对比图Fig.6 Comparison of variable universe fuzzy control

基于变论域模糊控制器相比模糊PID控制能够快速响应变化的风向，对于维持风电机组输出功率有更好的稳定性。表3给出了偏航系统的仿真对比统计数据。根据仿真统计数据分析，风轮转速和转速的波动明显降低，其中风轮转速的标准差降低了32.8%，风轮转矩的标准差降低了16.9%，明显提高了风电机组的稳定性。

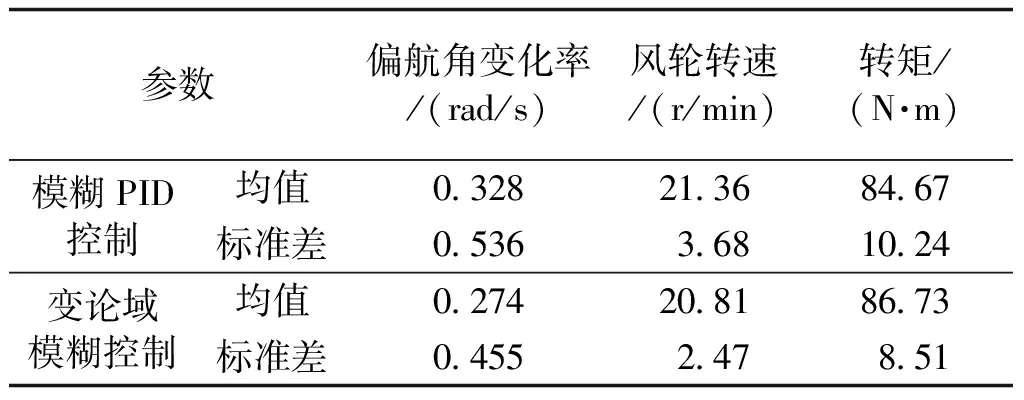
表3 仿真统计数据分析Tab.3 Statistical analysis of simulation

为了验证本文提出偏航控制方法的优越性，搭建了2MW风电机组的偏航控制实验平台，实验平台主要由偏航系统、上位机、偏航电机、风向标和信号采集装置等组成，如图7所示。采用四台功率为3kW的三相交流异步电动机作为偏航电机，偏航电机分别对称地立式安装在机舱的四个角落。

图7 风电机组偏航控制实验平台Fig.7 Yaw control experimental platform of wind turbine

图8为利用变论域模糊偏航控制策略进行偏航控制所得的偏航角度误差实时处理数据。在受风向等各种不利因素影响时，变论域模糊控制偏航角度保持2°以内的偏差，可见该控制的可行性。利用此策略准确对风的同时，发电量和机组振动情况相当，没有因此策略的引入而受任何影响。这样不仅提高了整个风电机组的效率，而且避免了偏航电机的频繁转动，降低了系统的机械损耗。图9为风电机组的输出功率，可见利用变论域模糊偏航控制策略能实现高性能的功率控制，稳定在额定值2MW左右。

图8 偏航角度误差实时处理数据Fig.8 Real-time data processing for yaw angle error

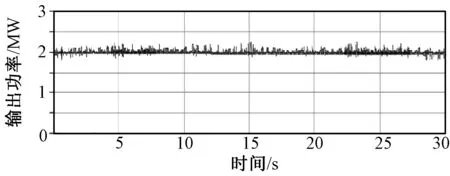
图9 风电机组输出功率Fig.9 Output power of wind turbine

表4给出了偏航系统实验对比统计数据。根据数据分析，变论域模糊偏航控制系统表现出的稳态性能明显优于模糊PID控制。利用变论域模糊控制偏航能保持2°以内的偏差，而偏航执行动作次数在整个实验周期内缩短3%左右，可延长风电机组的使用寿命。实验表明，基于变论域模糊偏航控制方法可以有效地减轻偏航执行机构的疲劳度，减少部件间的磨损，减少机组机舱的振动，对降低风电机组的故障发生率具有重要意义。

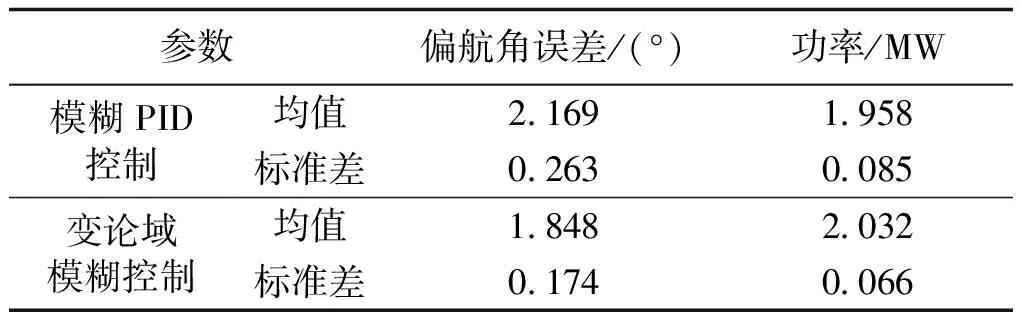
表4 偏航系统实验对比统计数据Tab.4 Statistical analysis of yaw control experiment

5 结论

大型风电机组偏航系统难以建立准确的数学模型，使用传统控制很难保证其效果。本文将变论域模糊控制方法运用到偏航控制，得出以下结论：

(1) 该控制器可以有效地提高偏航的控制精度，有助于保持电压稳定性，提高机组的输出功率。

(2) 所提变论域模糊偏航控制方法具有较强的鲁棒性，可对参数变化进行自整定。

(3) 文中方法解决传统控制难以兼顾动静态性能的缺点，偏航控制转矩脉动小，延长使用寿命。

[1] 李慧, 孙宏斌, 张芳(Li Hui, Sun Hongbin，Zhang Fang). 风电场风速分布模型研究综述(Review on models of wind speed distribution in wind farms) [J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2014, 33(8): 62-66.

[2] F A Farret, L L Pfitscher, D P Bernardon. Sensorless active yaw control for wind turbines [A]. The 27th Annual Conference of the IEEE Industrial Electronics Society, IECON’01 [C]. 2001. 2:1370-1375.

[3] Mona M, Karolos M Grigoriadis. Anti-windup linear parameter-varying control of pitch actuators in wind turbines [J]. Wind Energy, 2015, 18(2):187-200.

[4] Hassan H M, Eishafei A L, Farag W A, et al. A robust LMI-based pitch controller for large wind turbines [J]. Renewable Energy,2012, 44:63-71.

[5] X N Lin, Y X Zhuo, F Zhao, et al. Voltage sag problems in large-scale clustering wind farms[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2015, 10(1): 63-69.

[6] Christof D, Wout W, Mahmoud E. Monitoring resonant frequencies and damping values of an offshore wind turbine in parked conditions [J]. IET Renewable Power Generation, 2014, 8(4): 433-441.

[7] I Houtzager, J W Wingerden, M Verhaegen. Wind turbine load reduction by rejecting the periodic load disturbances [J]. Wind Energy, 2013,16(2):235-256.

[8] 韩兵, 周腊吾, 陈浩, 等(Han Bing, Zhou Lawu, Chen Hao, et al.). 基于RBF 神经网络的风电机组独立变桨控制(Based on RBF neural-network for Individual Pitch Control of Wind Turbine) [J]. 中国科学: 技术科学(Scientia Sinica Technogica), 2016, 46(3): 248-255.

[9] Jauch C, Islam S M, Nsen P S, et al. Design of a wind turbine pitch angle controller for power system stabilization [J]. Renewable Energy, 2007, 32(14): 2334-2349.

[10] Bianchi F D, Mantz R J, Christiansen C F. Gain scheduling control of variable speed wind energy conversion systems using quasi-LPV models [J].Control Engineering Practice,2005,13(2):247-255.

[11] K Tan, S Islam. Optimal control strategies in energy conversion of PMSG wind turbine system without mechanical sensors [J]. IEEE Transactions on Energy Conversion, 2004, 19(2): 392-399.

[12] 韩兵(Han Bing). 直驱永磁风力发电机组偏航系统的设计(The design of the yaw system for permanent-magnet generator direct driven by wind turbine) [D]. 长沙: 湖南大学(Changsha: Hunan University),2011. 21-31.

[13] 朴海国,王志新(Piao Haiguo, Wang Zhixin). 风电机组偏航Fuzzy-PID合成控制系统仿真(Simulation of fuzzy-PID synthesis yawing control system of wind turbine) [J].电工技术学报(Transactions of China Electrotechnical Society),2009,24(3):183-202.

[14] Y Q Zhang, Z Chen, M Cheng. Proportional resonant individual pitch control for mitigation of wind turbines loads [J]. IET Renewable Power Generation, 2013, 7(3): 191-200.

[15] 罗雅迪, 李静, 陈利杰, 等(Luo Yadi，Li Jing，Chen Lijie, et al.). 基于模糊理论的地区电网在线供电风险分析方法研究(Method study of on-line risk analysis for district grid) [J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2014, 33(12): 60-64.

[16] 岳士弘, 张绍杰, 李平(Yue Shihong, Zhang Shaojie, Li Ping). 变论域自适应模糊控制器失真率的计算(Computation of distortion ratio of adaptive fuzzy controller based on variable universe) [J]. 控制理论与应用(Control Theory & Applications), 2005, 22(5): 807-810.

Variable universe fuzzy control based yaw system of large wind turbine

HAN Bing1, ZHOU La-wu2, CHEN Hao3, TIAN Meng1, DENG Ning-feng1

(1. Hunan University, Changsha 410082, China; 2. Changsha University of Science and Technology, Changsha 410114, China; 3. Hunan Shiyou Electric Co. Ltd., Xiangtan 411101, China)

Positive significance of wind power on solving energy and environmental issues makes it to become the world’s fastest-growing new energy. Yaw control is a new research topic in study of wind turbines, and yaw control system is a typical nonlinear, time varying system, in which there are often a greater chance of parameter changes and large time-varying load and interference, so to establish a precise mathematical model is difficult. This paper presents a variable universe fuzzy yaw control strategy. The variable universe fuzzy control is combined with vane feedback control, and the wind data are quickly compared with power data recognition processing to realize the variable universe fuzzy control parameter self-tuning setting and control rules, so as to improve the yaw control system’s ability to adapt to wind disturbances and parameter changes. Finally, the experiments results show that variable universe fuzzy yaw control system has the advantages of fast dynamic response, strong anti-interference ability and robustness, etc.

large wind turbine; yaw system; variable universe; fuzzy control

2015-10-16

湖南省研究生科研创新项目(CX2016B131)

韩 兵(1986-)， 男， 湖南籍， 博士研究生， 研究方向为风力发电系统及其控制与新能源并网技术； 周腊吾(1965-)， 男， 湖南籍， 教授， 博士， 从事新型电机电器设计及控制、 新能源发电技术等研究。

TM614

A

1003-3076(2016)08-0015-06