一种基于单元数量控制的电动汽车充换电站电池充放电策略

张华栋， 杨 明， 李建祥， 刘海波， 卢 鹤， 刁浩然

(1. 国网山东省电力公司， 山东 济南 250001； 2. 电网智能化调度与控制教育部重点实验室，山东大学， 山东 济南 250061； 3. 国网山东省电力公司电力科学研究院， 山东 济南 250001)

一种基于单元数量控制的电动汽车充换电站电池充放电策略

张华栋1， 杨 明2， 李建祥3， 刘海波3， 卢 鹤2， 刁浩然2

(1. 国网山东省电力公司， 山东 济南 250001； 2. 电网智能化调度与控制教育部重点实验室，山东大学， 山东 济南 250061； 3. 国网山东省电力公司电力科学研究院， 山东 济南 250001)

电动汽车充换电站兼顾电力系统电源与负荷的双重属性，因而，充分挖掘其柔性、灵活的供需电特性，对其做出合理的充换电决策，具有十分重要的现实意义。传统的充放电控制策略以连续的充电电量为决策变量，然而，受电池荷电状态与数量限制，此类模型的最优解往往难以与现实对应。由此，基于日前分时电价，本文提出双向能量交换下以电池充放台数为决策变量的充换电站充放电二阶段优化控制方法，方法第一阶段以充换电站运行的最小支出费用为目标，在其基础上，第二阶段以站内满充电池数量最大为目标寻求最优充换电策略。以实际山东焦庄充换电站为例，比较了无序充电与本文有序充放电的充电负荷及费用支出，分析了本文提出的以电池充放台数为决策变量和传统方法以连续充电电量为决策变量的优化结果的区别，验证了本文提出方法的有效性。

电动汽车；充换电站；电池充放电；电池台数；二阶段优化

1 引言

发展电动汽车涉及环境保护、优化能源结构等国家战略问题，受到了多国政府的高度重视和大力支持[1]。大规模电动汽车接入电网，一方面，将对电力系统的运行和规划产生不容忽视的影响；另一方面，可以对充电负荷实施有序控制，甚至利用电池放电向电网运行提供支撑[2]。电动汽车充换电站是衔接电网与电动汽车之间的关键桥梁[3]，充分利用充换电站功率需求的柔性，研究其有序充换电策略，具有十分重要的现实意义。

电动汽车的充电模式可分电池充电(充电)和电池更换(换电)两种[4]。其中，换电模式具有操作方便、用户体验好、易于统一管理等特点，是最主要的电动汽车电能补给方式。在换电模式下，电动汽车充换电站可利用电池的储能特性，在电价低谷期对电池进行集中充电，降低充电成本；在满足换电需求的前提下，其还可以在电价高峰期向电网出售电能，获取卖电收益。上述有序充换电策略不仅可以对电网负荷起到良好的移峰填谷作用，而且有效降低了充换电站的充电成本，提高了充换电站运营的经济效益[5,6]。

目前，针对电动汽车充换电站充放电优化控制决策，许多学者开展了富有成效的研究。文献[6]考虑了大规模电动汽车用户的无序充电行为容易对电网造成“峰上加峰”等影响，以充换电站各时刻的充电功率为决策变量，建立多目标调度数学模型，采用自适应变异的粒子群算法对其求解，得出次日优化充电计划。文献[7]建立了以配电网网损最小为目标的电动汽车充电优化模型，考虑了电压幅值等约束，采用迭代修正节点电压的方法求解凸二次规划模型，运算速度可满足在线运行的要求。文献[8]提出建立最小化网络损耗和提高负荷因数的双层目标，利用随机规划方法优化充电方式。文献[9]考虑公交车的运行规律和耗电特性等因素，定量分析了车辆的日换电需求，以充电成本最小为首要目标，分别建立了两阶段和双目标优化充电模型。文献[10]基于电价预测，利用动态规划法优化各电池的充电时间，在不影响电池性能的前提下，降低了总充电成本。需要注意的是，以上控制策略均假设电动汽车电池的连续充电电量在充电过程中是完全可控的，未能深入考虑实际电动汽车的充电特性受电池容量、离散的电池数量和充电桩数量的限制，其得出的最优解往往在现实中难以实现[11]。

由此，本文基于分时电价机制，提出了双向能量交换模式下以离散的电池充放台数为决策变量的充换电站二阶段优化模型。其中，第一阶段以充换电站的支出费用最小为目标进行优化；第二阶段在第一阶段的求解基础上，选取使满充电池数量最大的充放电计划为模型的最优控制策略。算例基于实际山东焦庄充换电站的运营数据，比较了无序充电与本文提出的有序充放电情景下的充电负荷及费用支出，分析了以离散的电池充放台数为决策变量与以连续的充电电量为决策变量的优化结果的区别，验证了方法的实用性及有效性。

2 充换电站充放电优化控制方法

2.1 背景介绍

电动汽车充换电站是集充放电功能与换电功能于一体的大型电动汽车服务设施。换电服务模式下，其以满充电池与电动汽车用户进行电池交换来满足用户的换电需求，并根据交换电池所含的电能差取得收益。完成电池交换后，充换电站将电动汽车用户换下来的入站电池通过充电设备进行充放电操作，其换电过程如图1所示。

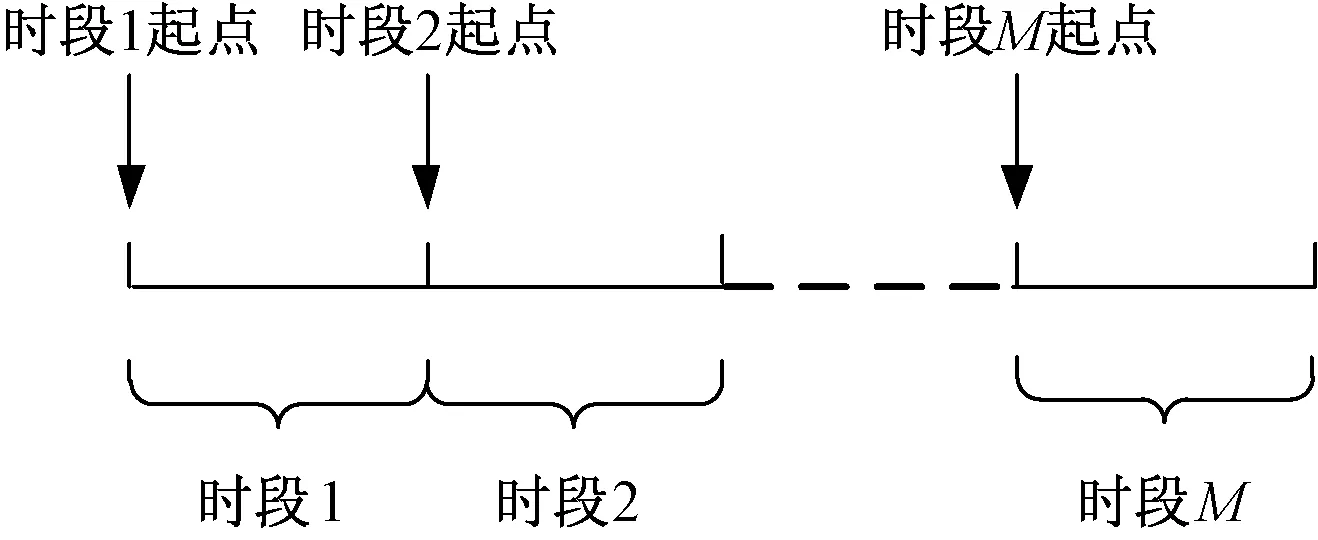
图1 换电过程示意图Fig.1 Figure of power exchange

图1中，充换电站的换电过程被划分为M个离散时段。由于实际电动汽车的入站时间是随机、难以掌控的，为方便分析，本文假设充换电站在距电动汽车入站时间最近的下一时段的起点完成对入站电池与满充电池的交换并继而安排入站电池的充放电计划。

2.2 电动汽车电池荷电状态离散化

建立以电池充放台数为决策变量的优化控制模型，首先，要将电池荷电状态离散化成不同的等级，且电池荷电等级数量需控制在调度可接受的范围

内。由于电动汽车锂电池的充放电过程可视为恒功率充放过程[12]，在单位时间步长内充电桩功率及充放电模式确定的情况下，通过模拟电池充放电过程，可实现电池荷电状态(State of charge, SOC)的离散化。

电池荷电状态定义为：在相同的放电倍率下，电池的可放电量与电池的额定容量之比[13]，即

(1)

式中，Qd为电池的剩余电量；Qt为电池的额定容量。容易理解，当电池满充，即达到充电截止电压时，SOC为100%；电池放电结束，即达到放电截止电压时，其SOC为0%。

电动汽车电池充放电过程模拟如图2所示。假设电池电量共被划分为k个不同的荷电等级，j(j=1,2,…,k)为电池的某一荷电状态等级标识，其可经单时段充电操作后到达jc(jc=1,2,…,k)荷电等级状态，又可由cj(cj=1,2,…,k)荷电等级状态的电池进行单时段充电得到。同理，若电池电量处于j荷电等级状态，其既可由dj(dj=1,2,…,k)荷电等级状态的电池进行单时段放电得到，又可经单时段放电操作后到达jd(jd=1,2,…,k)荷电等级状态。将荷电状态标识按照SOC的大小排序，即SOC1代表电量为0%的电池，SOCk代表SOC为100%的电池，SOCj表示荷电等级标识为j的电池的荷电状态。进而，设N1为空电电池的数量，Nk为满充电池的数量，Nj表示荷电等级标识为j的电池的数量。

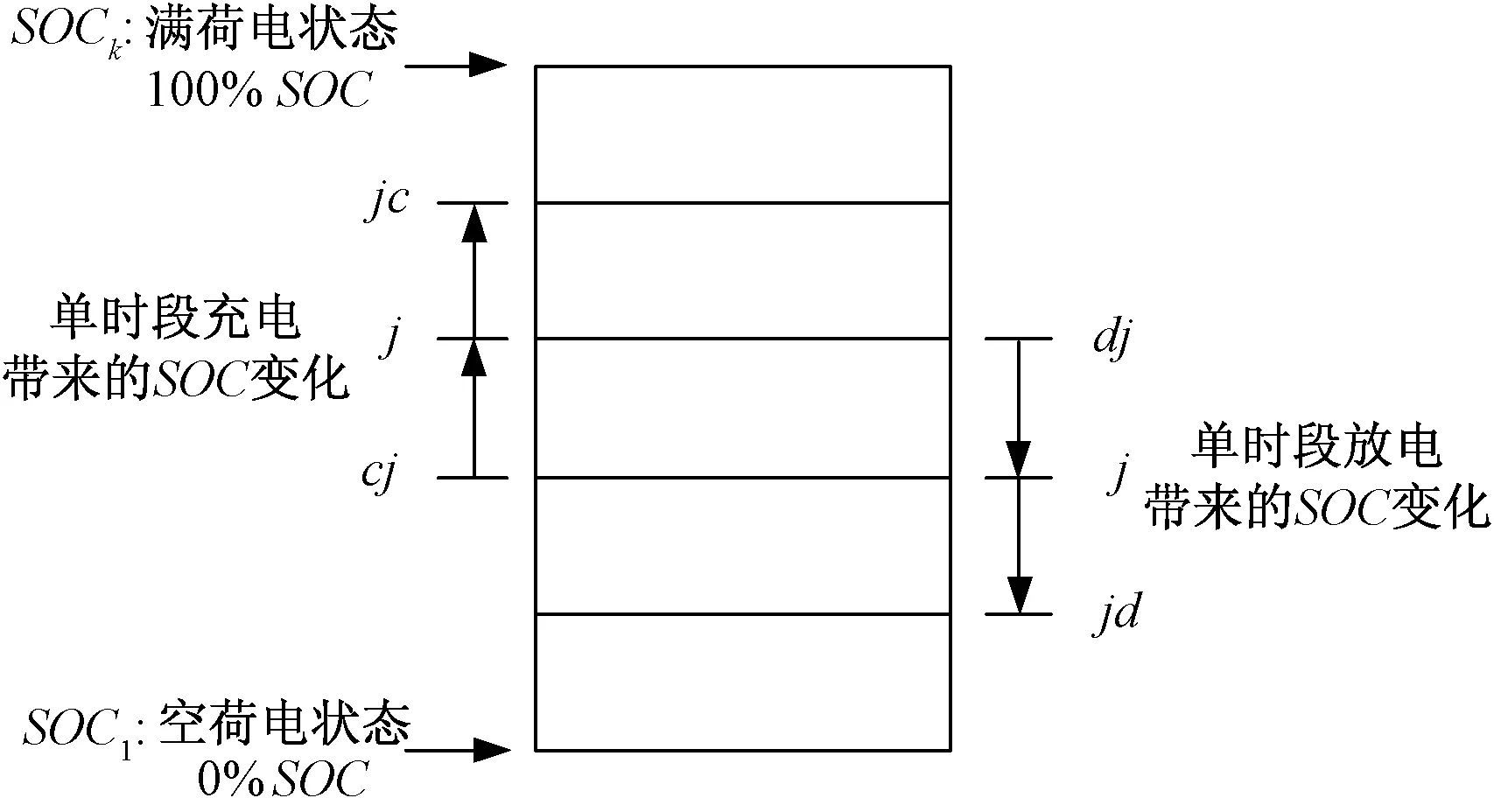
图2 电动汽车电池充放电过程示意图Fig.2 Electric vehicle battery charging and discharging process

2.3 传统模型

对于传统的以连续充放电电量为决策变量的电动汽车充换电站充放电优化控制，目前已有较多研究，其模型可表述为：

(2)

由模型可以看出，传统方法以充换电站运行的经济最优为目标，其考虑了总电量约束、充换电站功率约束及用户换电电量的需求约束，但没有考虑充换电站充电电量与用户换电电池数量以及充换电站充电电量与换电电池荷电状态之间的耦合关系。然而，在实际中，充换电站的充放电决策实质是对不同时段内电池充放台数的控制决策。而对充电电量的优化决策最终要通过离散电池的充放电实现，显然，不考虑电池荷电状态和数量的传统模型最优化解，在现实中可能无法得到可行的电池充放电方案。

2.4 基于电池充放台数的二阶段优化模型

在双向能量传输模式下，本文提出了一种以电池充放台数为决策变量的二阶段优化控制模型。其中，第一阶段优化以充换电站总支出费用最小为目标；第二阶段优化则在第一阶段的求解基础上，选取最大化满充电池数量的解为最终的优化决策，具体模型如下。

(1)目标函数

第一阶段优化以充换电站运行的经济性为目标，即向电网支出的总电费fs最少。将电池荷电状态离散后，式(2)的目标函数可表示为：

(3)

考虑到各时段起点时的满充电池数量越多，充换电站应对用户的换电需求的能力越强，因而，在第一阶段经济性最优的基础上，第二阶段优化以最大化各时段起点处的满充电池数量之和fx为目标，如式(4)所示：

(4)

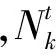
为保证第一阶段优化效果，第二阶段优化过程需要以第一阶段优化后的最小支出费用为约束，即充换电站的费用支出不大于第一阶段优化后的费用支出R，其表示为：

(5)

(2)约束条件

1)充换电站电池总量约束

(6)

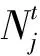
2)用户换电需求约束

用户换电需求约束要求充换电站在t时段起点的满充电池数量不小于在t时段预测的用户换电需求数量。本文采用设置概率置信度的方式来满足用户的换电需求，方法如下：首先，将用户的换电需求分为多个电量区间，并将其按由小到大依次排序，设置η为概率置信度，P(s)为用户换电需求电量区间为s的概率，从换电需求量最低的区间开始累加，直至概率总和达到置信度，并将最后一个区间记为q，则该区间q即为需要满足的用户换电需求电量，基于历史经验统计，可得到该换电需求区间q对应的换电电池数量及荷电等级状态，从而设置约束，如式(7)和式(8)所示：

(7)

(8)

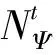
3)换电站充电桩数量约束

(9)

式中，Npum为充换电站充电桩的个数。该约束表示在t时段充换电站同时对电池进行充放电的数量不大于充换电站内充电桩的数量。

4)可操作的电池数量约束

(10)

该约束表示，t时段对荷电等级标识为j的电池充电操作数量和放电操作数量的和不大于t时段荷电等级标识为j的电池数量。

5)电池容量约束

(11)

6)充电桩功率约束

(12)

式中，pmax为充换电站充电桩的最大充放电功率，即额定充电功率；ppum为充换电站充电桩的实际充放电功率。该约束表明，在模型中，各充电桩功率数值恒定，以额定功率进行充电或放电操作。

7)电池荷电状态转移约束

对入站电池的荷电状态进行离散化后，入站电池的荷电状态集合为Ω，Ω={1,2,…,k}。其中满充电池的数量变化约束可表示为：

(13)

入站电池荷电等级的电池数量变化约束可表示为：

(14)

站内其他荷电等级的电池数量的变化约束可以表示为：

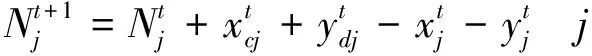
(15)

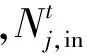
2.5 方法流程

式(3)～式(15)构成了完整的多目标混合整数规划模型，其决策变量为充换电站在各时段的不同荷电等级电池的充放台数。方法的应用流程如图3所示。首先，根据历史数据与经验，充换电站可统计得出电动汽车用户在各时段的换电需求区间的概率；同时，通过对入站电池充放电历史数据的统计，完成对入站电池荷电状态的离散化；进而，输入充换电站的原有贮存电池荷电状态及充电桩功率参数；最后，通过二阶段优化模型对电池充放数量进行优化求解，得到对电池充放台数的优化控制决策。

图3 本文方法流程Fig.3 Diagram of method presented in paper

3 算例分析

算例以实际山东临沂焦庄电动公交汽车充换电站运行数据为基础。焦庄站站内充电桩数量为20台，其充放电功率为30kW，站内单块电池容量为180kW·h，以1h为单位时间间隔，考虑对日前8∶00～17∶00共10个时段的充放电计划安排，利用本文方法对其实施充放电优化控制分析，算例使用GAMS软件进行编程求解。

3.1 入站电池SOC离散化分析及初始数据

通过统计焦庄站实际入站电池的单次充电电量样本，得到入站电池单次充电电量频率分布，如图4所示。实际入站电池SOC集中在67%和88%附近。进而，根据实际充电桩充电功率与电池容量数据，将电池荷电水平平均划分为7个等级状态(以下表中简称“状态”)，如表1所示，每个等级状态的电池电量为30kW·h。

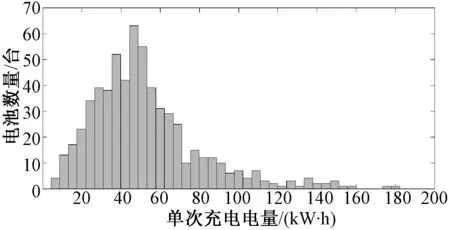
图4 入站电池单次充电电量分布图Fig.4 Distributions of battery on single charging

状态1234567SOC(%)01733506784100

假设选取的某典型日各时段电池入站数量及其荷电状态情况如表2所示。选取的该典型日下充换电站在初始时段已有贮存的电池数量及其荷电状态如表3所示，充换电站所在地区典型日的分时电价表如表4所示。

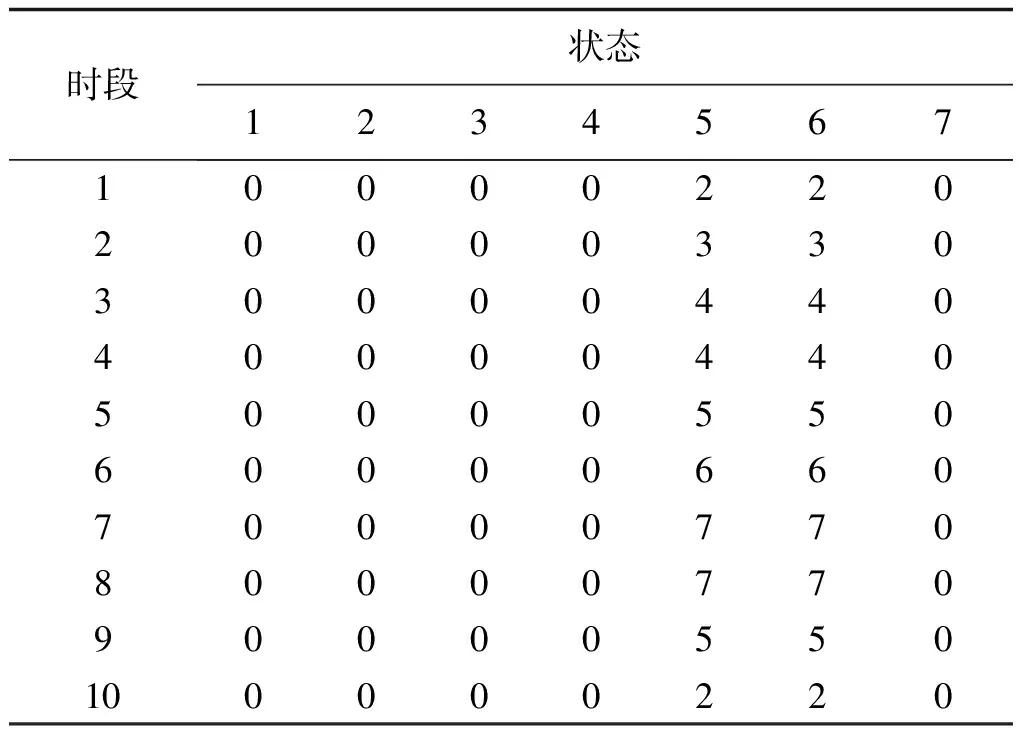
表2 入站电池数量信息表Tab.2 Quantities of inbound battery

3.2 充换电站用户换电需求概率分析

充换电站的用户换电需求样本数据来自山东临

沂焦庄电动公交充换电站的实际运营记录，样本统计了充换电站2014年6月14日至8月10日每日8:00～17:00每小时的换电需求电量，总计625组样本数据，其经验概率分布如图5所示。

表3 初始时段电池数量信息表Tab.3 Quantities and SOC of battery on first period

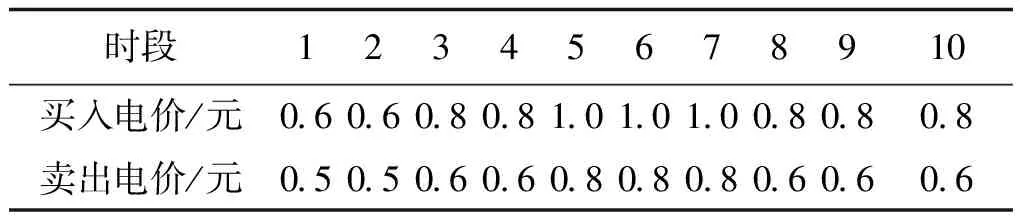
表4 分时电价表Tab.4 Table of TOU price

图5 样本数据经验概率分布Fig.5 Empirical probabilistic distribution

由图5可以看出，该充换电站用户的单时段换电需求上限为1000kW·h，下限为0。本文采用等区间划分方法将其划分为10个区间，各区间换电需求电量为100kW·h，如表5所示。换电区间数越大，说明充换电站在单时段的负荷需求量越大。

表5 充换电站换电需求划分Tab.5 Divisions of electric demand for swapping station

依据运营经验与历史数据，获得充换电站在该典型日下未来10个时段各换电需求区间的概率分布，如表6所示。其表示充换电站用户的各换电需求区间(表6中简写为“区间”)随时间变化的概率转移情况，表6中数值代表对应时段充换电站换电需求为其对应区间的概率大小。考虑式(7)和式(8)约束，本文设置换电需求概率置信度为0.8，得到各时段应满足的换电需求状态如表7所示。

3.3 无序充电模式下的充电计划

通常将电动汽车电池的即换即充模式(将电动汽车用户更换下的电池立即接入充电桩充电的模式)称作无序充电模式。算例基于选取的表2～表4的典型日信息，对电动汽车电池实施无序充电，其充电计划与表2所示的各时段的电池入站信息相同，即充换电站的充电计划不受分时电价的影响，一旦电池入站就立刻安排对其充电。由于采取即换即充策略，基于表4的分时电价，可计算得出充换电站的支出费用为3378元。

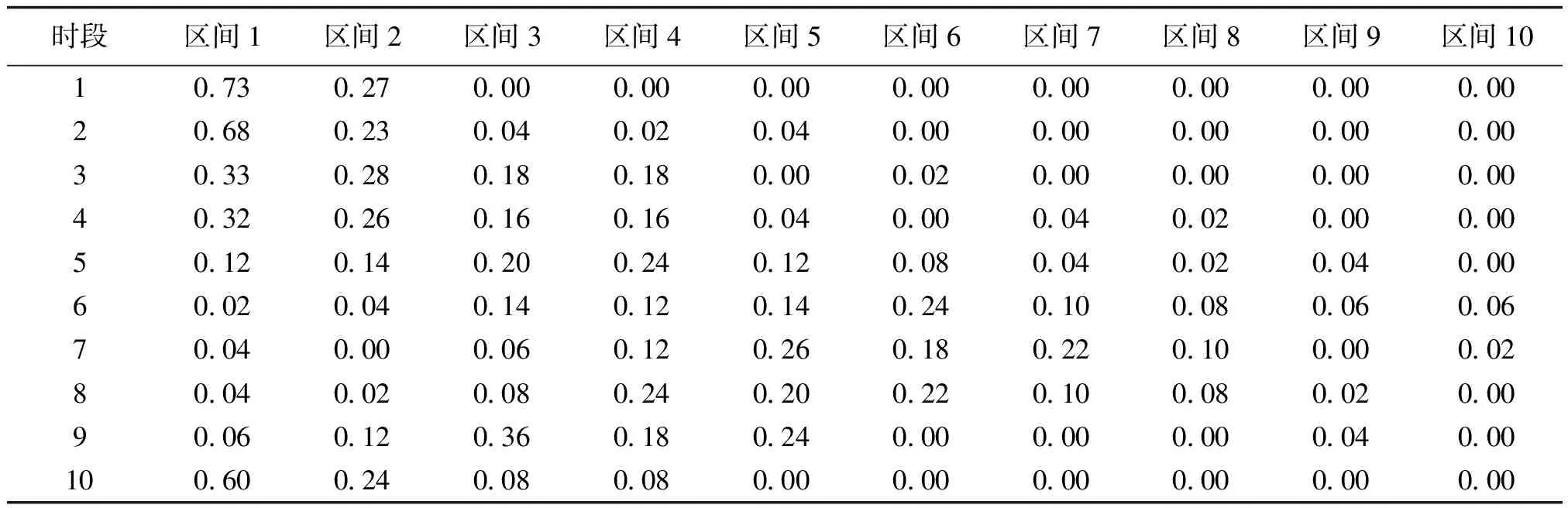
表6 充换电站换电需求区间的概率转移表Tab.6 State transition probabilities of electric demand range

表7 置信度为0.8的换电需求状态表Tab.7 Electric demand state at confidence level of 0.8

3.4 基于电池充放台数的优化控制

利用本文提出的基于电池充放台数的电动汽车电池充放电优化控制方法，一阶段优化后，各时段的电池充电安排如表8所示，各时段电池放电安排如表9所示，电池的荷电状态随时段变化的转移分布情况如表10所示。

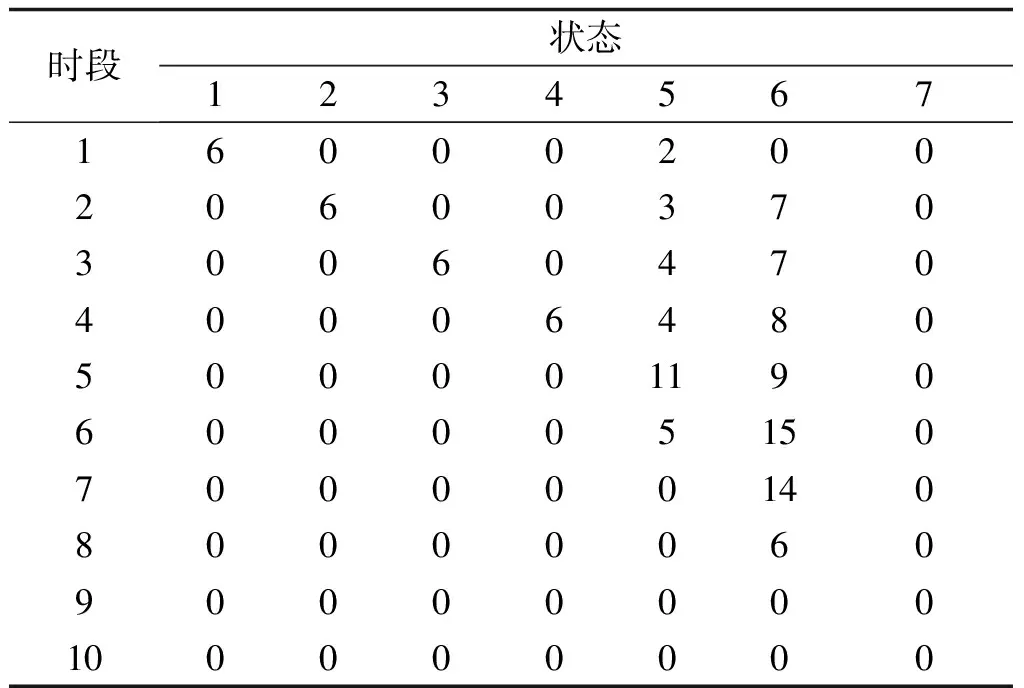
表8 一阶段优化后电池充电安排表

由表8和表9可以看出，受分时电价和用户换电需求的影响，充换电站的充电安排集中在1～7时段，而电池放电集中安排在8～10阶段。优化结果表明，当站内满充电池数量足以满足剩余时段用户的换电需求后，充换电站在7～10时段安排站内电池放电以减少支出费用。

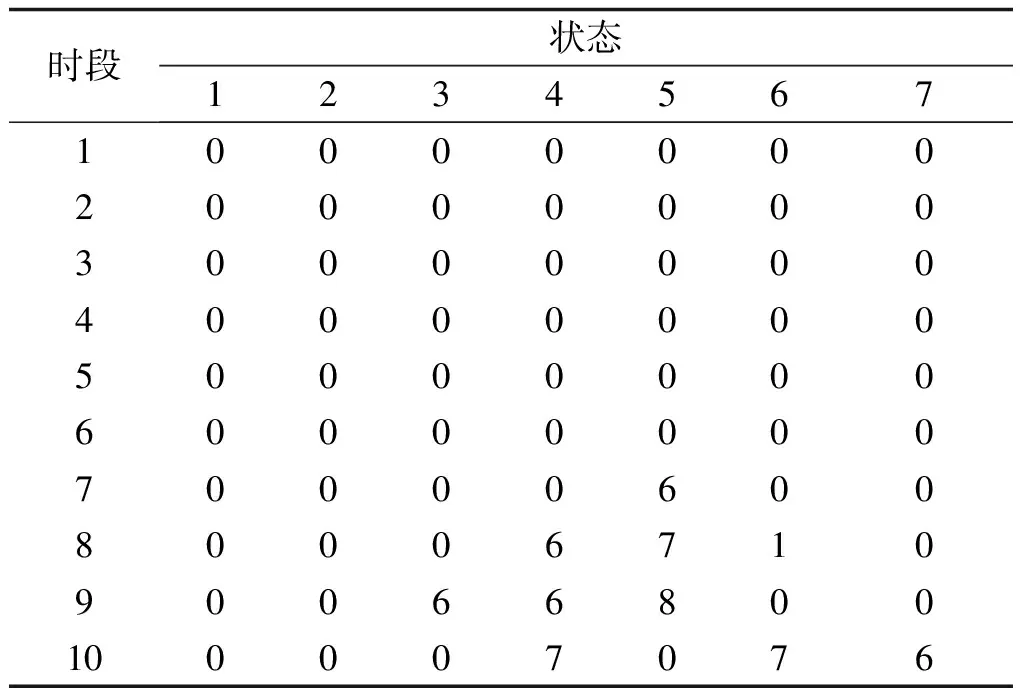
表9 一阶段优化后电池放电安排表Tab.9 Battery discharging schedules after first stage optimization

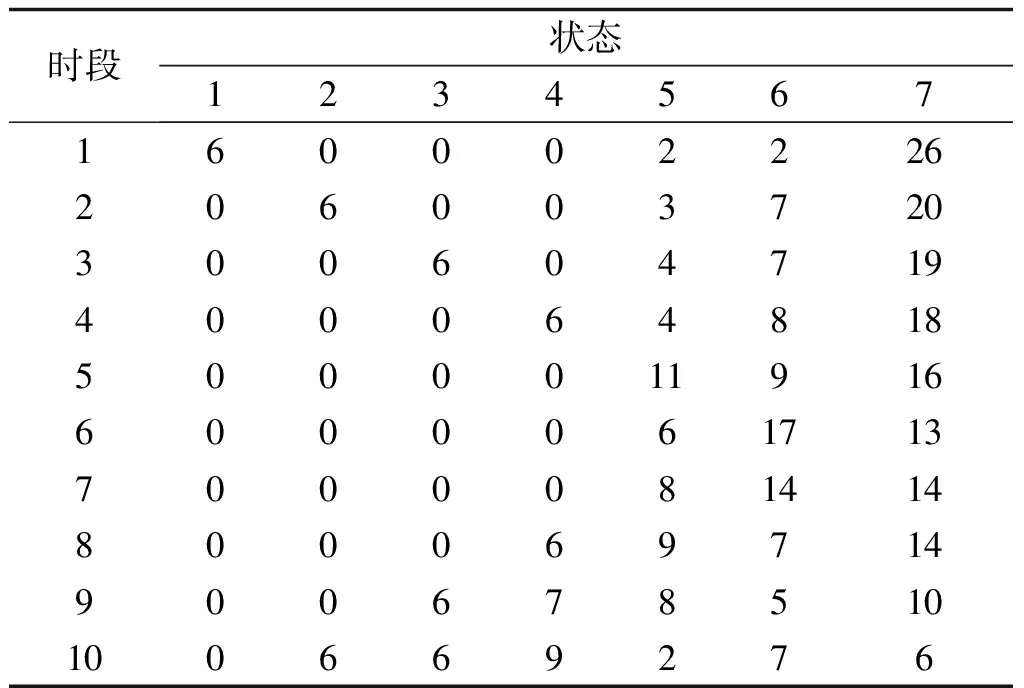
表10 一阶段优化后电池荷电状态转移分布表Tab.10 SOC transfer distributions after first-stage optimization

通常将优化后的电池充放行为称为有序充电模式。对比表2与表8、表9可以看出，经过有序优化后，充换电站在分时电价的平时及谷时充电功率增加，在峰时对电网进行反向送电。经计算，一阶段有序充电模式下，充换电站费用支出为1303元，相比无序充电，减少了费用支出1615元。支出费用的大幅减少表明一阶段充换电站的电池充放优化控制取得了理想的经济效果。

在一阶段优化的基础上进行二阶段寻优后，各时段的电池充、放电安排如表11和表12所示，电池荷电状态转移情况如表13所示。

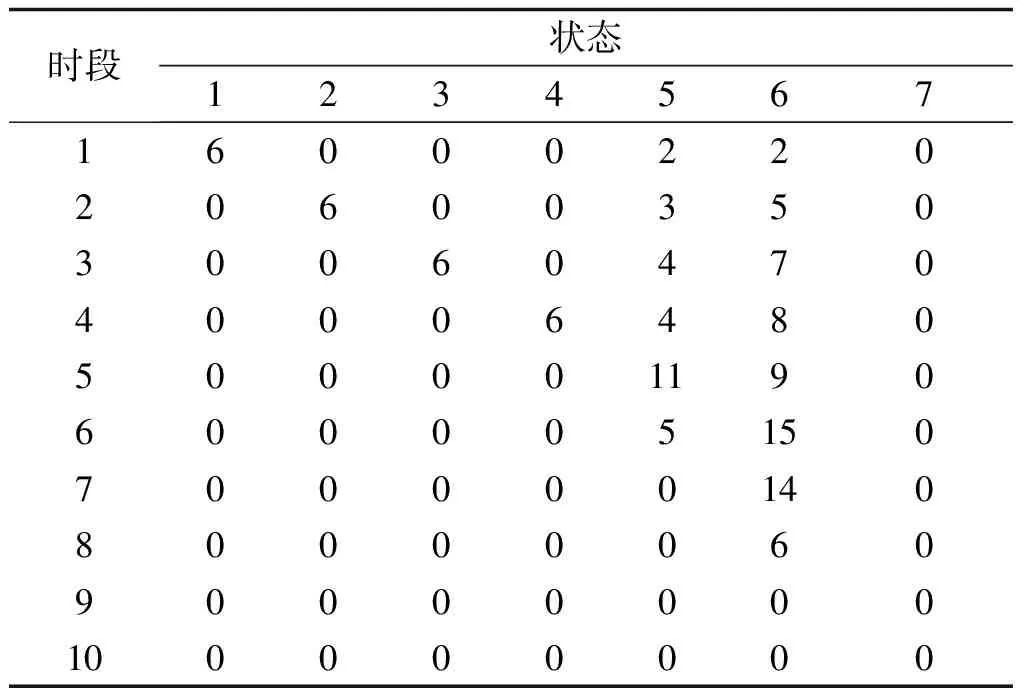
表11 二阶段优化后电池充电安排Tab.11 Battery charging schedules after second-stage optimization

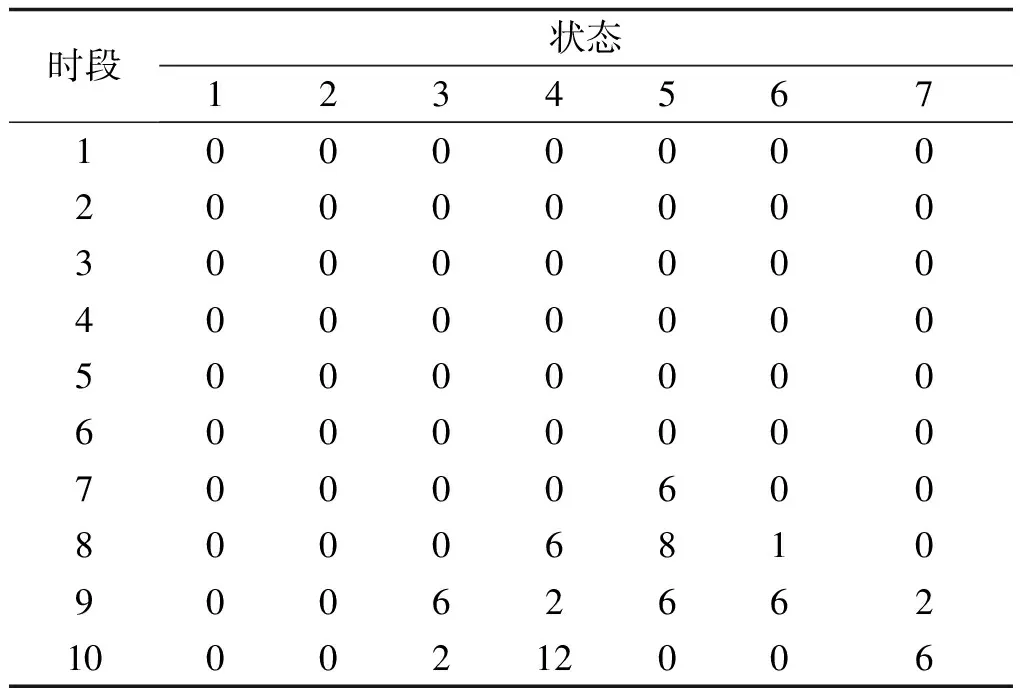
表12 二阶段优化后电池放电安排表Tab.12 Battery discharging schedules after second-stage optimization

经计算，二阶段优化后，充换电站的费用支出仍为1303元。但对比一阶段的优化结果可以发现，在进行二阶段优化后，电池的充电安排及放电安排发生了改变，此种改变的效果并没有造成充换电站支出费用的增加。进而，对比表13与表10可以发现，经二阶段优化后，电池荷电等级为7的满充电池数量较只进行一阶段优化的满充电池数量有所增加，有利于充换电站应对客户更换电池需求的随机不确定性，证明了本文方法的第二阶段优化在保证第一阶段优化的经济性前提下，可以最大化满充电池的数量。

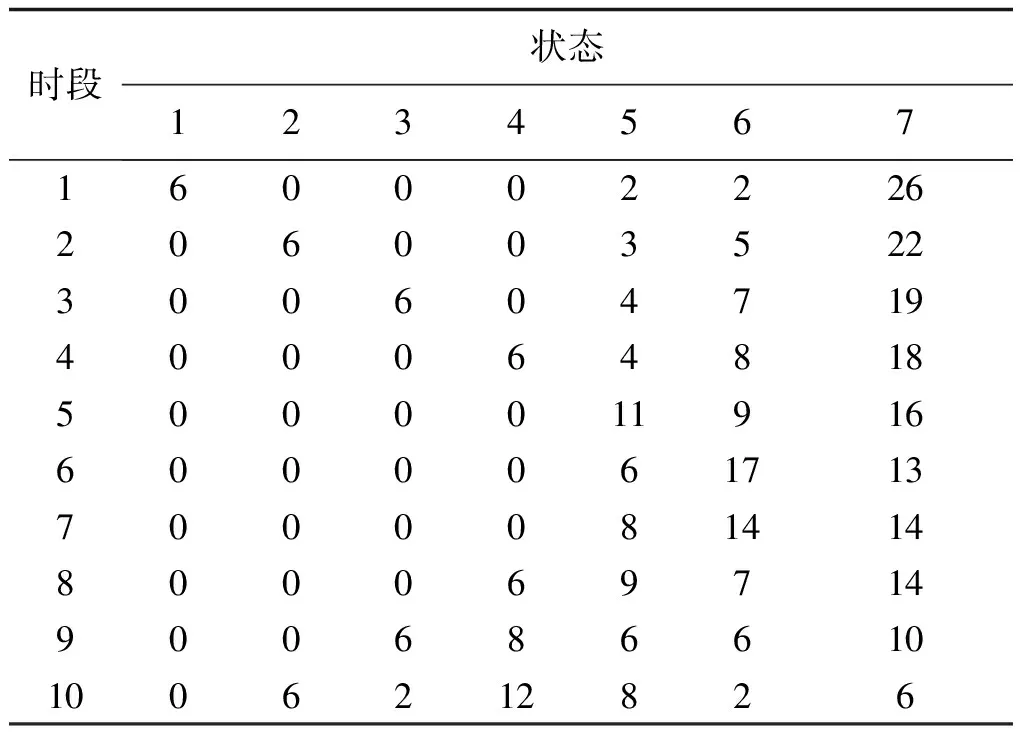
表13 二阶段优化后电池荷电状态转移表Tab.13 SOC transfer distributions after second-stage optimization

3.5 与传统模型的对比分析

采用传统模型式(2)的充换电站有序充电结果如表14所示。可以看出，传统模型优化控制得出的充换电站在各时段充电功率均为0，即全时段无电池充电安排，这是由于充换电站起始时段满充电池的总电量满足1～10时段的换出电量约束。由表2可知，该典型日充换电站1～5时段累计换出的满充电池数量为36块，而由表3可知，初始时段满充电池总数为30块。显然，如果在1～4时段不安排电池充电，那么在5～10时段，充换电站无法满足电动汽车用户的换电需求。这种情况产生的原因在于，传统模型以连续的电量为决策控制变量，而充换电站的总电量分配在多个离散的电池个体当中，电池的更换与电池的充放电操作必须依赖于离散的电池个体完成。因此，传统模型的优化结果可能出现在实际中不可行的情景。

表14 传统模型优化结果Tab.14 Optimization results of classic model

3.6 换电需求约束分析

本文模型采用满足设置的概率置信度的方式获得用户换电需求，并以换电需求最大区间的电池数量作为换电需求约束。显然，置信度的取值越大，充换电站满足用户换电需求的能力就越强，然而，也会因此导致充换电站的电能储备过剩，充换电站支出费用增加的问题。

不同的概率置信度设置将会得出不同的用户换电需求结果，因而会导致不同的换电策略及支出费用，现模拟两个不同的换电需求场景来分析充换电站的费用支出情况，结果如表15和表16所示。

表15 换电需求情况表(场景1)Tab.15 Battery exchange demands of scenario 1

表16 换电需求情况表(场景2)Tab.16 Battery exchange demands of scenario 2

可以看出，场景1与场景2的换电需求不同，将其分别作为本文模型的换电需求约束，可计算出经二阶段优化后，充换电站的支出费用分别为1296元和960元，验证了在不同的换电需求下，充换电站的支出费用不同的结论。

4 结论

本文首先分析了充换电站电池荷电状态离散化的过程及传统模型的不足，在此基础上提出了以电池充放台数为决策变量的二阶段优化模型。算例结果表明，本文方法可以根据分时电价合理安排电池充放，相比于无序充电模式，大幅降低了充换电站的支出费用；克服了传统模型的解在现实中未必可行的缺点；算例部分还对换电需求约束的不同导致的决策结果的影响进行了对比分析。本文方法为电动汽车充换电站充放电控制提供了一种有效思路。

[1] 田立亭, 张明霞, 汪奂伶 (Tian Liting, Zhang Mingxia, Wang Huanling). 电动汽车对电网影响的评估和解决方案 (Evaluation and solutions for electric vehicles’ impact on the grid)[J]. 中国电机工程学报 (Proceeding of the CSEE), 2012, 32(31): 43-49.

[2] 张文亮, 武斌, 李武峰, 等 (Zhang Wenliang, Wu Bin, Li Wufeng, et al.). 我国纯电动汽车的发展方向及能源供给模式的探讨 (Discussion on development trend of battery electric vehicles in china and its energy supply mode)[J]. 电网技术(Power System Technology), 2009, 33(4): 1-5.

[3] 吴健生, 李小舟 (Wu Jiansheng, Li Xiaozhou). 基于最大熵理论的多类型电动汽车充换电站规划 (Coordinated planning of multi-type electric vehicle charging stations based on maximal entropy theory)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2015, 34(9):29-32.

[4] 何承坤, 王丽芳, 张仲石,等 (He Chengkun, Wang Lifang, Zhang Zhongshi, et al.). 基于容差控制的电动汽车动力系统动态负载模拟 (Dynamic load emulation for electric vehicle powertrain based on error tolerance control)[J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy), 2015, 34(6):22-26.

[5] 陈良亮, 张浩, 倪峰, 等 (Chen Liangliang, Zhang Hao, Ni Feng, et al.). 电动汽车能源供给设施建设现状与发展探讨 (Present situation and development trend for construction of electric vehicle energy supply infrastructure) [J]. 电力系统自动化(Automation of Electric Power Systems), 2011, 35(14): 11-17.

[6] 田文奇, 和敬涵, 姜久春, 等 (Tian Wenqi, He Jinghan, Jiang Jiuchun, et al.). 基于自适应变异粒子群算法的电动汽车换电池站充电调度多目标优化(Multi-objective optimization of charging dispatching for electric vehicle battery swapping station based on adaptive mutation particle swarm optimization)[J]. 电网技术(Power System Technology), 2012, 36(11): 25-29.

[7] 占恺峤, 宋永华, 胡泽春, 等(Zhan Kaiqiao, Song Yonghua, Hu Zechun, et al.). 以降损为目标的电动汽车有序充电优化(Coordination of electric vehicle charging to minimize active power losses)[J]. 中国电机工程学报(Proceedings of the CSEE), 2012, 32(31): 11-18.

[8] Clement-Nyns K, Haesen E, Driesen J. The impact of charging plug-in hybrid electric vehicles on a residential distribution grid[J]. IEEE Transactions on Power Systems, 2010, 25(1): 371-380.

[9] 阳岳希, 胡泽春, 宋永华(Yang Yuexi, Hu Zechun, Song Yonghua). 电动公交充换电站的优化运行研究(Research on optimal operation of battery swapping and charging station for electric buses)[J]. 中国电机工程学报(Proceedings of the CSEE), 2012, 32(31): 35-42.

[10] Rotering N, Ilic M. Optimal charge control of plug-in hybrid electric vehicles in deregulated electricity markets[J]. IEEE Transactions on Power Systems, 2011, 26(3): 1021-1029.

[11] 戎晓雪, 刘熙媛, 孙启明, 等(Rong Xiaoxue, Liu Xiyuan, Sun Qiming, et al.). 电动汽车充换电站换电池的有序充电优化(Coordinated charging strategy for battery in EV charging and switching station)[J]. 电力建设(Electric Power Construction), 2015 (7): 120-125.

[12] 宋永华, 胡泽春, 阳岳希 (Song Yonghua, Hu Zechun, Yang Yuexi). 电动汽车电池的现状及发展趋势 (Present status and development trend of batteries for electric vehicles)[J]. 电网技术(Power System Technology), 2011, 35(4): 1-7.

[13] 荣雅君, 杨伟, 牛欢,等 (Rong Yajun, Yang Wei, Niu Huan, et al.). 基于BP-EKF算法的电动汽车电池管理系统SOC精准估计 (Accurate estimation of SOC value of electric vehicle battery based on EKF algorithm optimized by BP neural network)[J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy), 2015, 34(9):22-28.

Strategy of battery charging and discharging for electric vehicle swapping station based on battery unit number

ZHANG Hua-dong1, YANG Ming2, LI Jian-xiang3, LIU Hai-bo3, LU He2, DIAO Hao-ran2

(1. State Grid Shandong Province Electric Company, Jinan 250001, China; 2. Key Laboratory of Power System Intelligent Dispatch and Control, Shandong University, Jinan 250061, China; 3. Electric Power Research Institute of State Grid Shandong Province Electric Company, Jinan 250001, China)

Electric vehicle swapping station has both the power source and load properties, therefore, it is of great practical significance to fully exploit its electrical characteristics of supply and demand to make a reasonable decision for charge of power. Classic charging and discharging control strategies take continuous charging electric power as their control variable, however, by the battery state of charge and quantitative restrictions, the optimal solutions of such models are often difficult to match the reality. Based on time price of electricity, a two level optimization model about electric vehicle swapping station control is proposed, with number of swapping batteries as the decision variable. The first level of the model is to optimize the operating cost, and the second level is to maximize the number of full batteries without increasing the operating cost. Taking Jiao Zhuang swapping station in Shandong province as an example, this paper compares charging load and costs at disorderly charging and orderly charging, and analyzes the differences between the results of optimization and traditional optimization, which demonstrates the effectiveness of the method proposed.

electric vehicle; swapping station; battery charging and discharging; number of battery; two-stage programming

2015-12-18

国家重点基础研究发展计划(973计划)项目(2013CB228205)

张华栋(1976-), 男, 山东籍, 高级工程师, 硕士, 研究方向为营销管理, 电动汽车运营管理； 杨 明(1980-), 男, 山东籍, 副教授, 博士, 研究方向为电力系统运行与控制。

TM 73

A

1003-3076(2016)08-0057-09