基于双论域的一般多粒度模糊粗糙集

孙文鑫

（重庆水利电力职业技术学院基础部，重庆永川 402160）

基于双论域的一般多粒度模糊粗糙集

孙文鑫

（重庆水利电力职业技术学院基础部，重庆永川 402160）

首先定义了各论域上的支撑函数；其次通过支撑函数分别给出了不同论域一般多粒度模糊下上近似算子的定义，建立了双论域的一般多粒度模糊粗糙集模型；此外，还讨论了各近似算子的性质．

粗糙集；多粒度；双论域

由Z．Pawlak在1982年提出的粗糙集理论［1］是一种处理不确定性的数学工具［2］．如今，它已成功的应用到了各个领域，如模式识别［3］、数据挖掘［4］等．而由Zadeh提出的模糊集理论也是一种处理不确定性问题的数学工具，然而这两种数学理论处理的不确定性问题是完全不同的，因此一些研究者便将Pawlak粗糙集理论和模糊集理论结合起来提出了模糊粗糙集模型和粗糙模糊集模型［5，6］．

粗糙集研究的另一方面还集中在粒计算上．Zadeh在1979年首先提出了粒计算的概念并讨论了模糊信息粒度［7］．Hobbs在1985年提出了粒的概念［8］．从粒计算的观点来看，经典的Pawlak粗糙集模型可以视为是基于一个粒度（等价关系）的粗糙集模型，当由多个粒度来划分论域时，便会出现如下情况：

情形1：至少存在一个粒度使得该元素一定属于刻画的概念；

情形2：至少存在一个粒度使得该元素可能属于刻画的概念；

情形3：存在某些粒度使得该元素一定属于刻画的概念；

情形4：存在某些粒度使得该元素可能属于刻画的概念；

情形5：所有的粒度都使得该元素一定属于刻画的概念；

情形6：所有的粒度都使得该元素可能属于刻画的概念；

从上述情形出发，一些研究者已经将粗糙集模型推广到了多粒度粗糙集模型．为了将多粒度粗糙集模型更好的应用到实际问题中，文献［9］提出了基于等价关系的多粒度粗糙集模型．

1 基于双论域的模糊粗糙集

下面将介绍一些必备的理论知识［10］。

定义1设u和V是两个非空论域，若R是u×V上的子集，则称R是从论域u到论域V上的一个二元关系．

定义2称三元组（u，V，R）为一般的近似空间，其中u和V是两个非空的有限集称为论域，R是u×V上的任意一个二元关系．

定义3设（u，V，R）是一般的近似空间，分别定义两个算子Rs：U｜→P（V）Rp：V｜→P（U）称Rs（x）为x对于关系R的后继领域，Rp（y）为y对于关系R的前继领域．

定义4设（U，V，R）是一个一般的近似空间，对于任意的模糊集A∈F（U），B∈F（V），分别定义论域U，V上的两个近似算子如下：

则分别称RU（A）和RU（A）为论域U上模糊集A的下近似和上近似，而别称为论域V上模糊集B的下近似和上近似．

2 基于双论域的一般多粒度模糊粗糙集

介绍双论域上的一般多粒度模糊粗糙集．

定义5设U，V是两个不同的非空论域，是上的个不同的二元关系，对于x∈U，y∈V，分别定义

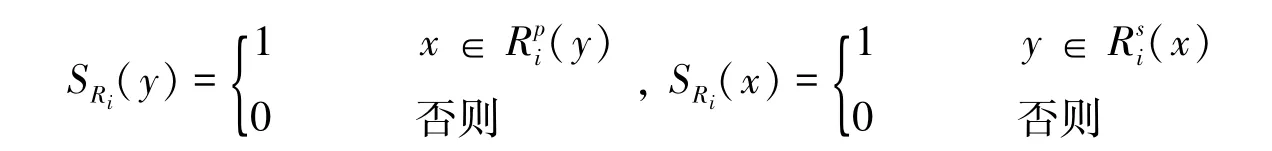
分别称SRi（y）为y在关系Ri的支撑函数，SRi（x）为x在关系Ri的支撑函数．

定义6设U，V是两个不同的非空论域，是上的个不同的二元关系，对于任意的β∈（0．5，1］，A∈F（U），定义

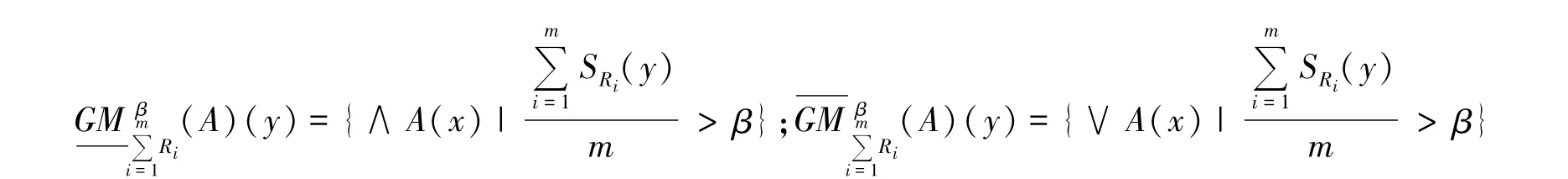
根据论域u上一般多粒度模糊粗糙集下上近似算子的定义可得到以下性质．

性质1设u，V是两个不同的非空论域，Ri（i＝1，…，m）是u×V上的m个不同二元关系，对于任意的β∈（0．5，1］，A，A*∈F（u），则有以下性质成立。

证明：（1）对于任意的，有

（2）如果A⊆A*，则对于任意的y∈V，有A（y）≤A*（y）．故

同理可证得性质成立．

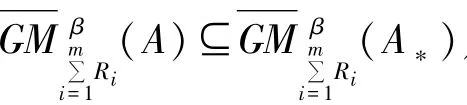
（3）对于任意的y∈V，有

（4）对于任意的y∈V，有（A∩A*）（y）≤A（y）且（A∩A*）（y）≤A*（y）。根据性质（2），故性质成立．

同理可证得性质（5）和（6）成立．

定义7设U，V是两个不同的非空论域，Ri（i＝1，…，m）是u×V上的m个不同的二元关系，对于任意的β∈（0．5，1］，B∈F（V），定义

称分别为论域V上模糊集B的一般多粒度粗糙模糊下近似和上近似．如果，则称B是论域V上的一般多粒度模糊可定义的，否则称B是论域V上的一般多粒度模糊粗糙的．

性质2设u，V是两个不同的非空论域，Ri（i＝1，…，m）是u×V的m个不同的二元关系，对于任意的β∈（0．5，1］，B，B*∈F（V），则有以下性质成立．

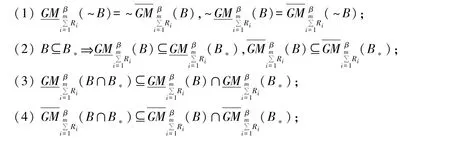
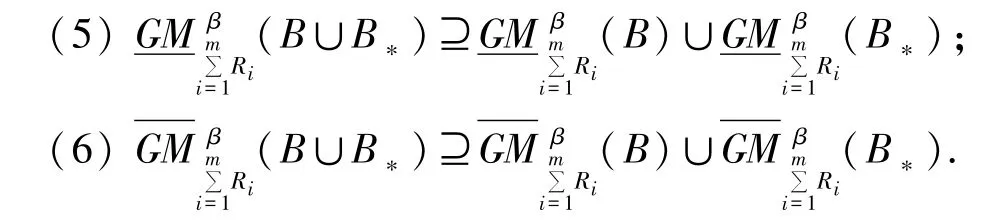
证明：证明过程类似于性质1的证明过程．

3 结 论

将双论域上的模糊粗糙集和粒计算理论结合起来建立了双论域上的一般多粒度模糊粗糙集模型．为了更好的建立模型，定义了各论域上的支撑函数，并讨论研究了各论域上近似算子的性质．研究为双论域上多粒度的研究奠定了理论基础．

［1］PAWLAK Z．International Journal of Computer and Information Sciences［J］．Rough Sets 1982（11）：341-356

［2］代春艳．粗糙集理论及其应用发展综述［J］．重庆工商大学学报：自然科学版，2004，21（6）：575-579

［3］ANAN V S，NARASU M M，SUBR D K．Tree Structure for Efficient Data Mining Using Rough Sets［J］．Pattern Recognition Letter，2003（24）：851-862

［4］CHAN C C，A Rough Set Approach to Attribute Generalization in Data Mining［J］．Information Sciences，1998（107）：169-176

［5］DUBIOS D，PRADE H，Rough Fuzzy Sets and Fuzzy Rough Sets［J］．International Journal of General Systems，1990（17）：191-209

［6］CHEN D G，ZHAO S Y．LocalReduction of Decision System with Fuzzy Rough Sets［J］．Fuzzy Sets and Systems，2010（161）：1871-1883

［7］ZADEH L A．Fuzzy Sets and Information Granularity［J］．Advances in Fuzzy Set Theory and Application，North Holland Publishing，1979（60）：1211-1214

［8］HOBBS J R．Granularity Proc of Ijcal［J］．Los Angeles，1985（18）：432-435．

［9］QIAN Y H，LIANG Y．A Multi-granulation Rough Set［J］．Information Sciences，2010（180）：949-970

［10］XU W H，SUN W X．Fuzzy Rough Set Models Over Two Universes［J］．International Journal of Machine Learning and Cybernetics，2013（4）：631-645

Generalized Multi-granulation Fuzzy Rough Set Based on Two Universes

SUN Wen-xing

（Chongqing Water Resources and Electric Engineering College Chongqing，402160，China）

Firstly，this paper defines the support function of the universes，with which the approximation operators of the generalized multi-granulation fuzzy rough set is defined，and then generalized multi-granulation fuzzy rough set based on two universes model is constructed．In addition，the properties of the approximation operators are discussed．

Rough set；multi-granulation；two universes

O380

A

1672－058X（2015）03－0012－04

10．16055／j．issn．1672－058X．2015．0003．003

2014－09－01；

2014－10－12．

孙文鑫（1988－），女，河南焦作人，硕士研究生，从事粗糙集和模糊集的研究．