考虑磁致伸缩效应的可控饱和电抗器电磁振动分析

杨意妹， 祝丽花， 王 斌， 杨庆新

(电工电能新技术天津市重点实验室， 天津工业大学， 天津 300387)

考虑磁致伸缩效应的可控饱和电抗器电磁振动分析

杨意妹， 祝丽花， 王 斌， 杨庆新

(电工电能新技术天津市重点实验室， 天津工业大学， 天津 300387)

可控饱和电抗器由于其优良的工作特性，在电力系统和有色冶金等多种行业得到了广泛的应用。作为补偿用电设备，可控饱和电抗器能连续不断地调整其电抗值，改变其容量。由于可控饱和电抗器铁心结构的特殊性及交直流共同作用的工作特点，铁心的振动噪声较大，其振动噪声问题成为可控饱和电抗器应用发展的制约因素之一。本文基于开源型有限元分析软件建立了磁路-机械耦合模型，考虑电磁力与磁致伸缩效应作用，完成了不同工作状态下铁心磁场和振动的数值分析，得到了其磁场、振动的分布情况，为在设计上减少电抗器振动噪声提供理论依据和计算方法。

可控饱和电抗器； 电磁力； 磁致伸缩效应； 电磁振动

1 引言

电力在传输尤其是在高压输电中，维持无功功率平衡尤为重要。在现有的无功补偿装置中，可控饱和电抗器具有优良的工作特性，可根据系统传输功率大小调节吸收容性容量，避免投切无功补偿装置产生的高频操作过电压、过电流及谐波等，改善系统潮流分布，提高系统稳定性[1-3]。可控饱和电抗器由于其铁心结构的特殊性及其工作特点，运行时产生的电磁振动及噪声引起了国内外学者的广泛关注。对可控饱和电抗器铁心振动产生机理的研究主要集中在对电磁力的研究，忽略了铁心硅钢片的磁致伸缩效应的影响。

国内外学者对铁磁材料的磁致伸缩特性进行了研究。英国学者Anthony J. Moses和泰国学者Sakda Somkun等提出了无取向电工硅钢片的二维磁致伸缩特性测量模型及其影响因子，并给出了磁致伸缩测量结果[4,5]。韩国学者Pan Seok Shin和Hee Jun Cheung利用磁弹性有限元方法推导了磁场与形变的关系[6]。但磁致伸缩效应对电抗器振动噪声的影响研究仍鲜见。日本佐贺大学Gao Yanhui和Kazyhiro Muramatsu等学者考虑磁致伸缩效应和电磁力的作用计算分析了干式铁心电抗器的磁场和振动情况，计算得到水平方向位移大于垂直方向位移，其中电磁力通过磁场计算得到，磁致伸缩力采用等效节点力法计算得到[7-9]。文献[8]提出利用高硬度绝缘材料填充铁心间隙降低电抗器铁心振动噪声的方法，但文中忽略了铁心的实际结构，计算误差较大。文献[10,11]分析了不同的铁心结构对磁通密度和磁致伸缩的影响，得出在设计较低噪声变压器时应考虑铁心结构的结论。但文中将铁心简化成矩形和方形结构，与实际结构相差较大。文献[12]分析了电抗器稳态时的磁场和振动分布，提出通过改变铁心材料特性降低铁心振动，分析中忽略了硅钢片各向异性特性。

本文考虑磁致伸缩效应对可控饱和电抗器铁心振动的影响，建立二维电抗器电磁-机械耦合模型，对铁心不同饱和程度下的磁场和振动进行数值分析，得到铁心磁场、振动的分布情况，得出磁致伸缩效应对电抗器铁心振动的影响。

2 可控饱和电抗器原理

可控饱和电抗器借助磁饱和现象，通过调节控制系统的激磁来改变铁心磁化状态，进而可改变铁心的磁导率和电感值，达到连续调节容量的目的[13]。电抗器电感的计算公式为：

(1)

式中，L为电感器的电感；N为电抗器绕组匝数；μ为铁心磁导率，μ=μ0μr，其中μ0为真空磁导率，μr为相对磁导率；Ac为磁路的截面积；l为磁路的有效长度。

由式(1)可知，当电抗器型号确定后，电感值的大小仅正比于铁心磁导率，而铁心的磁导率与铁心的饱和程度成反比。

图1为单相可控饱和电抗器的结构原理图。可控饱和电抗器在交流电源的一个周期内的运行状态分析如下：

(1)当交流电源工作在正半周期时，等效磁路如图2(a)所示。晶闸管K1导通，在绕组回路中产生激磁环流id1、id2，两者叠加即为产生的实际磁通。此时，对铁心柱2起去磁作用，对铁心柱1起助磁作用。

(2)当交流电源工作在负半周期时，等效磁路如图2(b)所示。晶闸管K2导通，在绕组回路中产生激磁环流id3、id4，两者叠加即为产生的实际磁通。此时，对铁心柱2起助磁作用，对铁心柱1起去磁作用。

(3)K1、K2截止，二极管D导通时，等效磁路如图2(c)所示。此时，控制绕组不起作用，电抗器相当于一台空载变压器，电流很小，磁导率最大，输出容量最小。

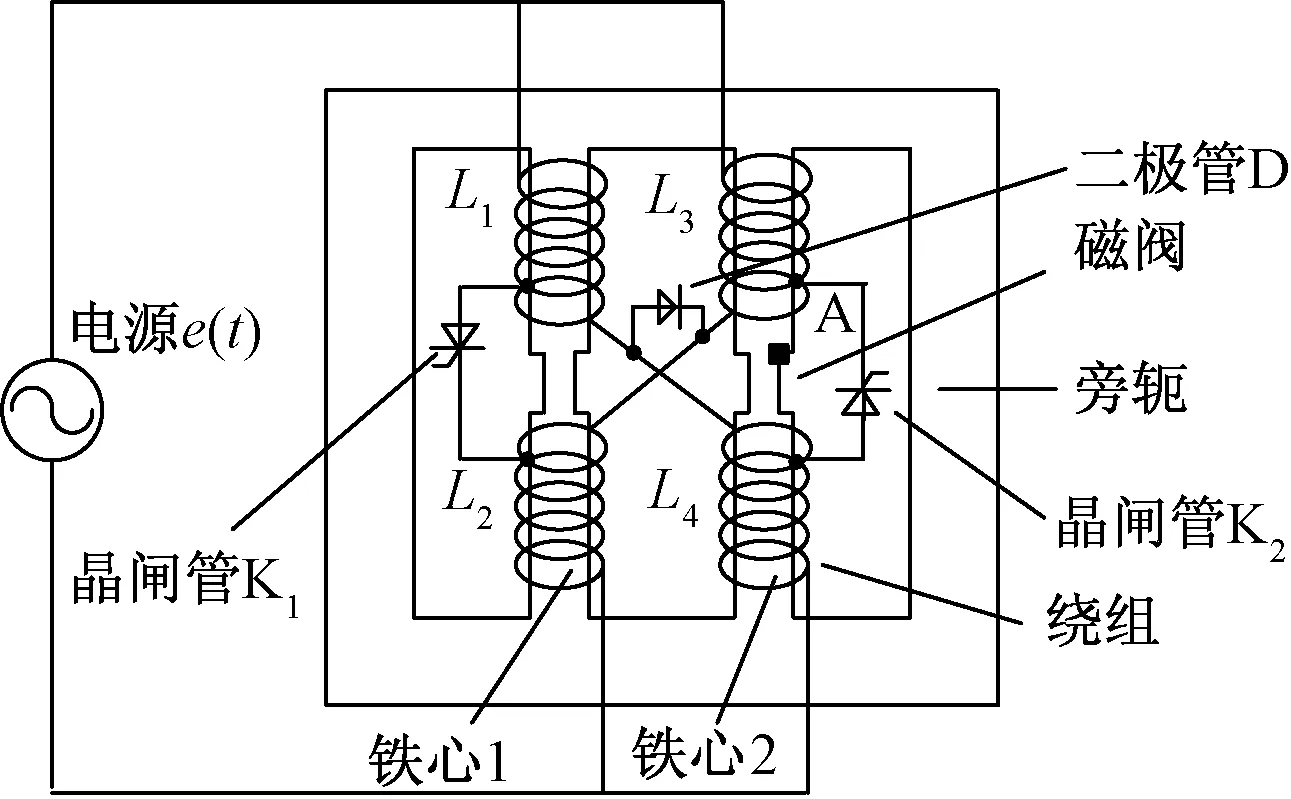
图1 单相可控饱和电抗器结构图Fig.1 Structure of single-phase MCR

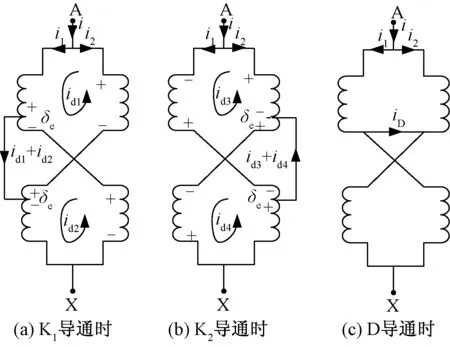
图2 单相可控饱和电抗器等效磁路Fig.2 Equivalent magnetic circuit of MCR

3 考虑磁致伸缩效应的电抗器振动电磁-机械耦合分析

3.1 磁场分析

电抗器运行时，由铁心构成的磁路中存在着交变电磁场，电抗器铁心磁场的计算方程为[14]：

(2)

(3)

(4)

式中，J为外电流密度；ecoil为沿z方向的单位矢量；Icoil为线圈电流；S为线圈截面积；σ为介质电导率；A为矢量磁位；B为磁感应强度；H为磁场强度。

将式(2)计算得到的外电流密度作为磁场中的激励源加载到式(3)中，结合式(4)即可求出铁心中磁通密度B及矢量磁位A。

3.2 磁致伸缩应力分析

磁致伸缩效应即磁性材料在外部磁场作用下，内部随机取向的磁畴发生旋转，磁化方向趋于一致，导致其长度沿磁力线的方向伸长或缩短[10, 12]，从而内部产生磁致伸缩应力。本文采用弹性力学方法计算电抗器铁心的磁致伸缩应力。

根据磁通密度和磁致伸缩峰峰值的关系，利用三次样条插值的方法将测得的磁致伸缩蝴蝶曲线处理成一条平滑的磁致伸缩单值曲线，磁致伸缩应变可由磁场强度与单值磁致伸缩特性曲线插值计算得到[15]。将插值得到的磁致伸缩应变作为机械场分析的初始应变，依据弹性力学基本原理，应力和应变呈线性关系，磁致伸缩应力可表示为：

σ=Dε

(5)

式中，σ为磁致伸缩应力；D为弹性张量；ε为磁致伸缩应变。

对于二维线弹性材料，弹性张量D可表示为：

(6)

式中，E为弹性材料的杨氏模量；α为弹性材料的泊松比。

3.3 机械振动分析

忽略电抗器铁心系统阻尼的影响，电抗器铁心振动方程为：

(7)

(8)

式中，ρ为密度；u为位移；F为外力。

本文通过对电抗器铁心电磁场的计算，根据铁心磁通密度及硅钢片磁致伸缩特性插值计算得到磁致伸缩应变，由弹性力学基本原理得到磁致伸缩应力，结合结构瞬态动力学分析，即可得到铁心的振动。

4 仿真计算分析

4.1 仿真模型分析

本文以一台10kV、500kvar的单相四柱可控饱和电抗器为研究对象，考虑电磁力和磁致伸缩效应作用时对不同控制电压下的电磁特性、振动位移、加速度进行瞬态分析，铁心采用35WW300硅钢片。可控饱和电抗器剖分后的求解模型如图3所示。

图3 单相可控饱和电抗器网格划分图Fig.3 Mesh of MCR

为了提高计算速度，将求解器步长设置为0.001s，计算时间为两个周期。同时为了提高求解精度，剖分时将铁心磁阀位置细化，网格剖分共含有21032个三角单元。

在有限元计算时，采用外电路方式进行激励，场路耦合电路如图4所示。其中，Es为直流控制源，为电路提供直流励磁，R0、R1分别为交流回路和直流回路的电阻。

图4 场路耦合电路Fig.4 Field-circuit coupling circuit

4.2 计算结果分析

通过用有限元法计算电磁力与磁致伸缩效应对电抗器铁心振动的影响，分析了不同控制电压下电抗器铁心的振动情况。在瞬态求解器下，对电抗器铁心是否考虑磁致伸缩效应产生的结果进行对比分析，并计算电抗器在不同控制电压下铁心中磁场、振动位移、振动加速度的大小。

图5为某一时刻不同控制电压下电抗器铁心的磁力线和磁通密度云图。由图5(a)、图5(b)和图5(c)对比可知，随着控制电压的增大，铁心尤其是磁阀处的磁通密度在不断增大，铁心的饱和程度不断增加。磁阀处磁通密度最大分别为1.07T、1.68T、1.83T。

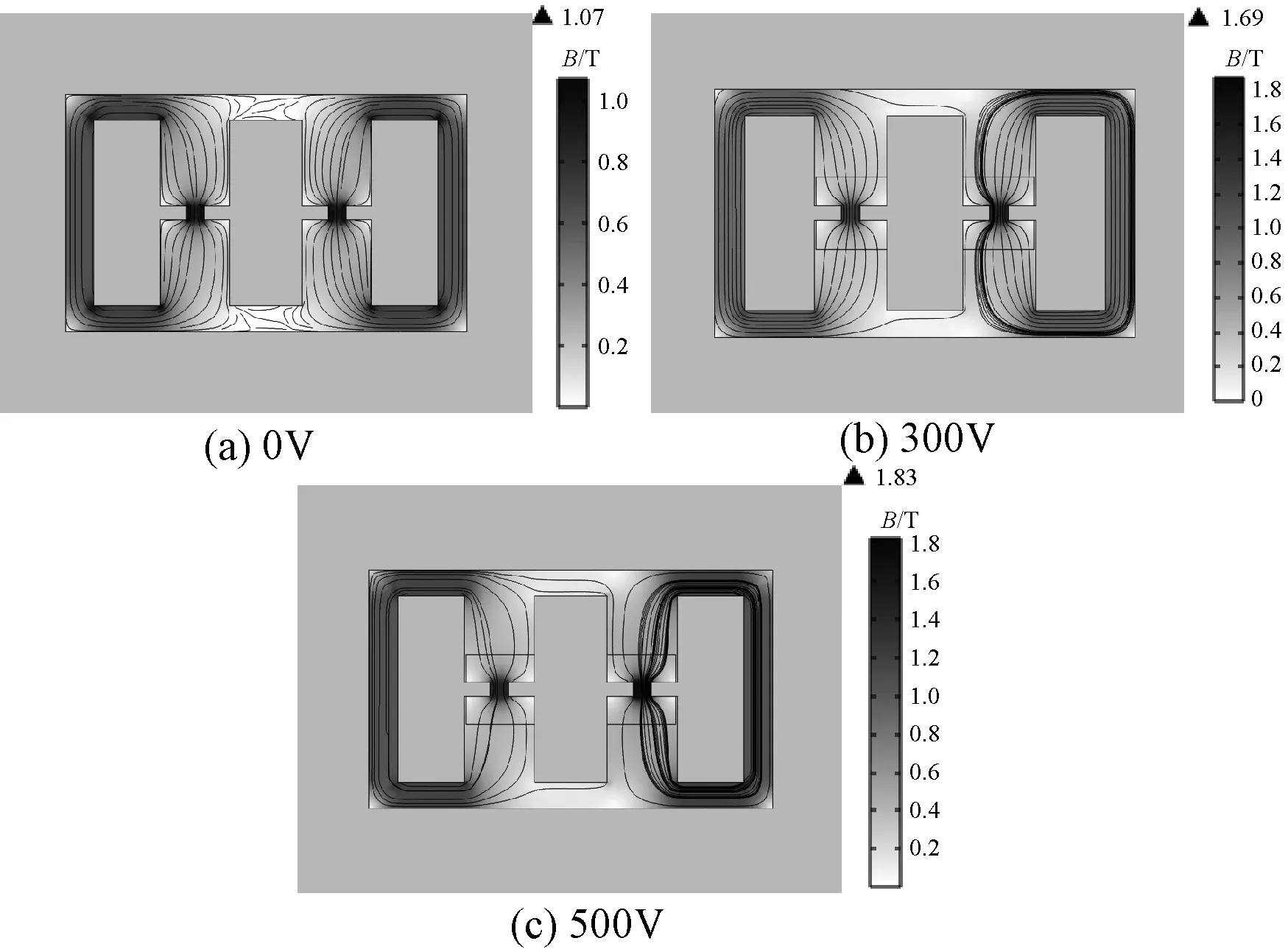
图5 不同控制电压下磁通密度分布Fig.5 Magnetic flux density distribution under different control voltages

图6为仅考虑电磁力时，300V控制电压下不同时刻电抗器铁心的变形分布。图7为考虑磁致伸缩时，300V控制电压下不同时刻电抗器铁心的变形分布。

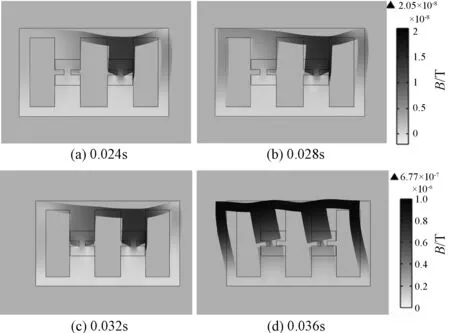
图6 仅电磁力时不同时刻铁心变形Fig.6 Deformations of different times with electromagnetic force

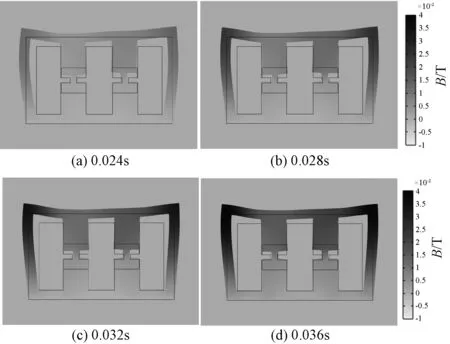
图7 考虑磁致伸缩效应不同时刻铁心变形Fig.7 Deformations of different times with electromagnetic force and MS

将可控饱和电抗器底部设置为固定约束，其余部分设置为自由。图6与图7对比可知，磁致伸缩对电抗器铁心的振动影响比较明显，考虑磁致伸缩效应时电抗器铁心的变形量明显大于电磁力单独作用时铁心的变形。

对不同控制电压下考虑电磁力与磁致伸缩效应引起的铁心振动位移及加速度进行了计算。图8为仅考虑电磁力时不同控制电压下磁阀处质点A的振动位移大小比较。图9和图10为考虑磁致伸缩效应时不同控制电压下磁阀处质点A的振动位移及加速度大小。

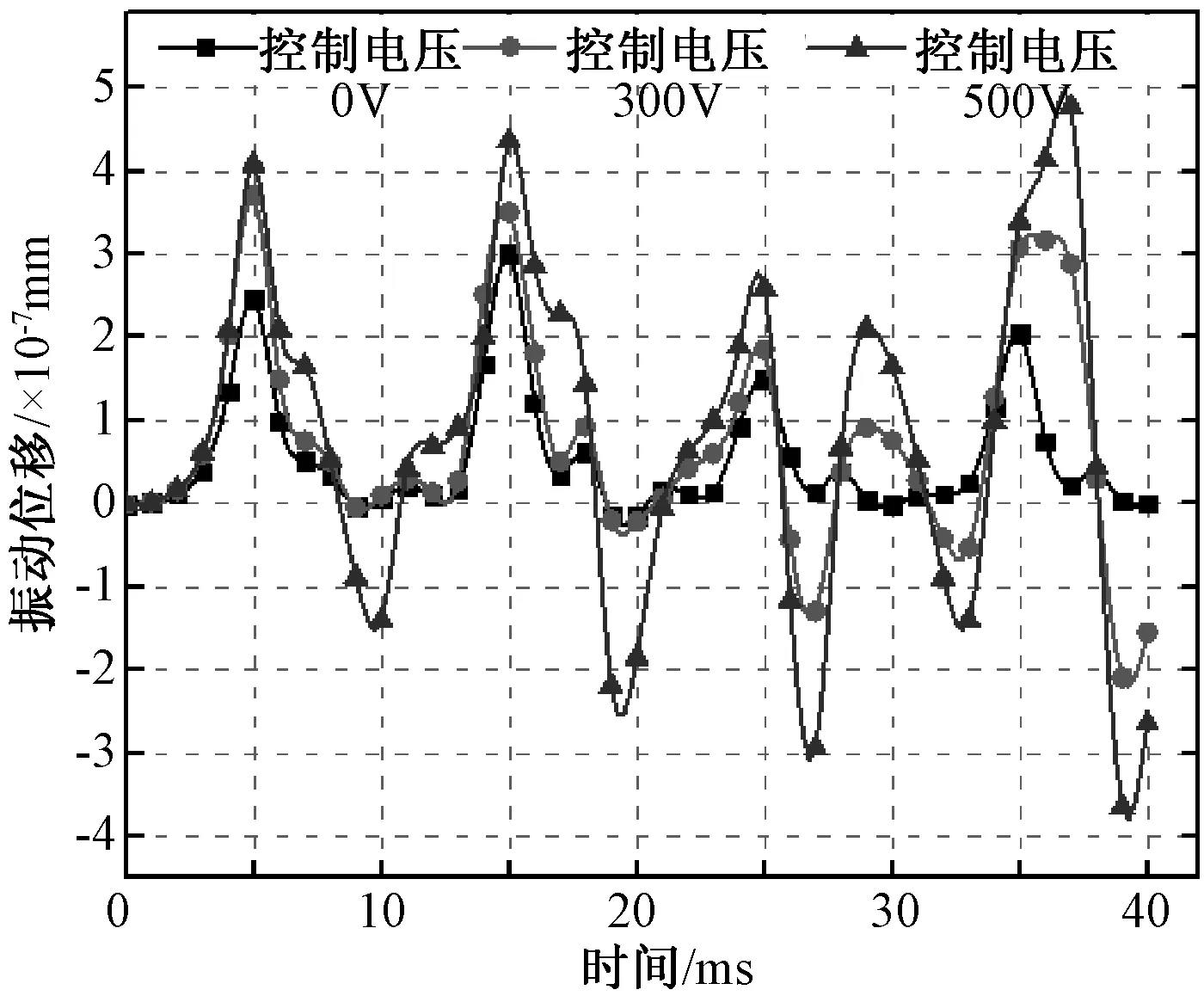
图8 质点在不同控制电压下振动位移比较(仅电磁力)Fig.8 Vibration displacement of particles under different control voltages (only electromagnetic)

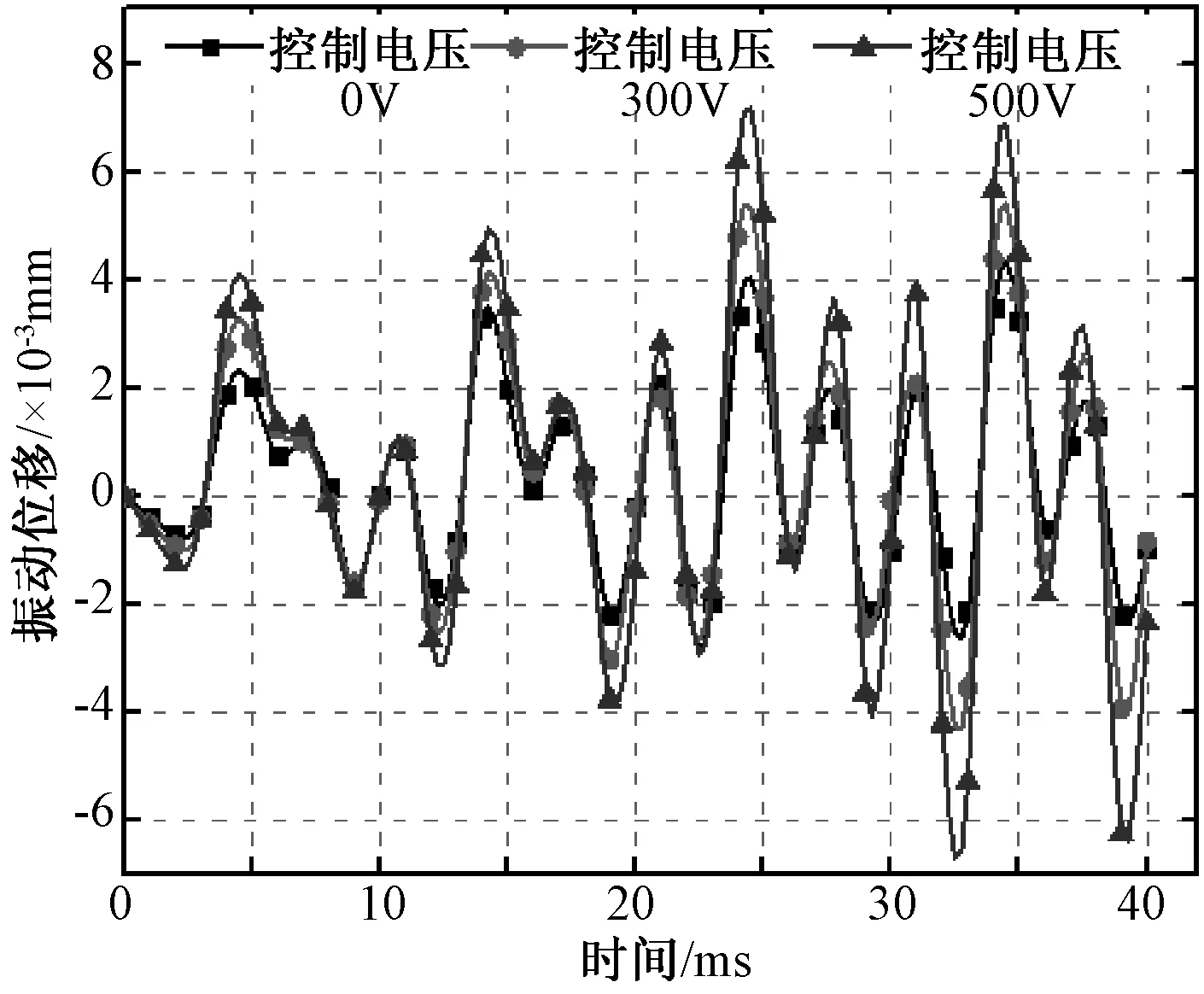
图9 质点在不同控制电压下振动位移比较Fig.9 Vibration displacement of particles under different control voltages

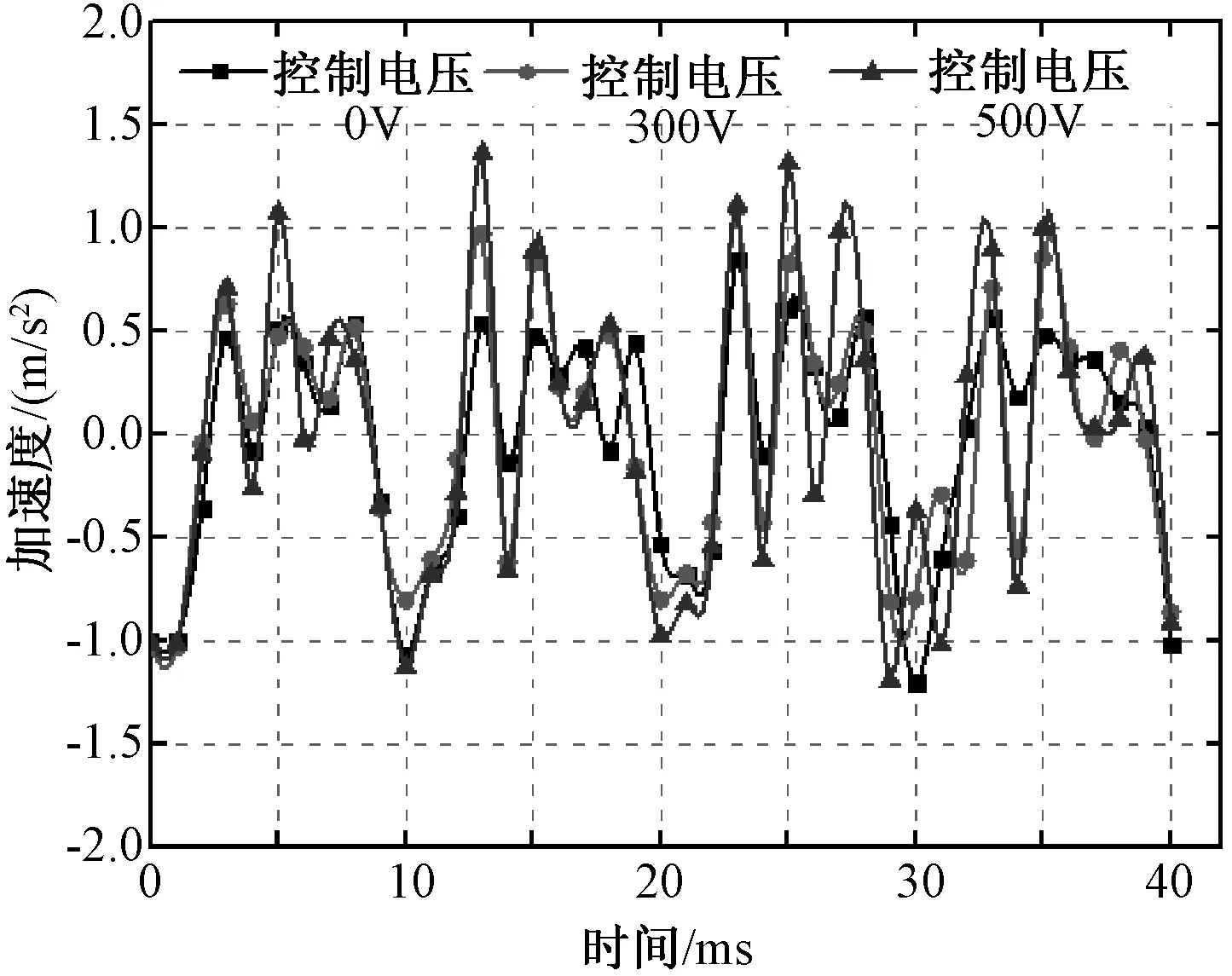
图10 质点在不同控制电压下振动加速度比较Fig.10 Vibration acceleration of particles under different control voltages

由图8～图10可以看出，仅电磁力作用时，控制电压分别为0V、300V、500V计算的振动位移最大值分别为2.89e-7mm、3.72e-7mm、4.95e-7mm；电磁力和磁致伸缩共同作用时，控制电压分别为0V、300V、500V计算的振动位移最大值为4.23 e-3mm、5.13e-3mm、6.72e-3mm，计算的振动加速度分别为0.78m/s2、1.25m/s2、1.41m/s2。

对比图8～图10中的三组曲线可知，随着控制电压的增大，电抗器铁心的振动位移、振动加速度也随之增大，产生的电磁振动越剧烈。图8与图9质点A 在不同力作用下产生的位移对比可看出，考虑磁致伸缩效应铁心产生的位移比仅电磁力作用时铁心产生的位移增大了104倍，可见磁致伸缩效应对铁心振动的影响要明显大于电磁力对铁心振动的影响，所以对电抗器电磁振动分析时磁致伸缩效应不可忽视。

5 结论

本文以10kV、500kvar单相可控饱和电抗器为例，进行了电磁-机械振动的二维有限元数值分析，分析了不同控制电压下电抗器铁心周围磁场分布、振动位移及振动加速度的大小。分析结果表明，当导通角不变时，电抗器铁心的振动强度随控制电压的增大而增大，控制电压越大，铁心中磁通密度越大，铁心达到饱和的时间越长，振动对电抗器铁心造成的危害就越大，所以应按要求严格控制直流电压的大小。计算结果显示，可控饱和电抗器的振动是由电磁力和磁致伸缩效应引起的，但磁致伸缩效应引起的铁心变形明显大于电磁力引起的铁心变形。所以在生产可控饱和电抗器时，在考虑成本的基础上应选择直流偏磁条件下磁性能稳定和磁致伸缩较小的硅钢片，尽量减小由磁致伸缩效应引起的铁心振动。

[1] 郑涛, 赵彦杰(Zheng Tao, Zhao Yanjie). 超/特高压可控并联电抗器关键技术综述(Overview of key techniques of EHV/UHV controllable shunt reactor)[J]. 电力系统自动化(Automation of Electric Power Systems), 2014, 38(7):127-135.

[2] Liu Wenye, Luo Longfu, Dong Shuda, et al. Overview of power controllable reactor technology[J]. Energy Procedia, 2012, 17: 483-491.

[3] Chong Shao, Xi Nian Liu, Wei Zhou Wang, et al. Study on promoting integration of large scale wind employed the 750kV controllable shunt reactor[A]. 5th China International Conference on Electricity Distribution[C]. 2012. 1-3.

[4] A J Moses, P I Anderson, S Somkun. Modeling 2-D magnetostriction in nonoriented electrical steels using a simple magnetic domain model[J]. IEEE Transactions on Magnetics, 2015, 51(5): 1-7.

[5] S Somkun, A J Moses, P I Anderson. Measurement and modeling of 2-D magnetostriction of nonoriented electrical steel[J]. IEEE Transactions on Magnetics, 2012, 48(2): 711-714.

[6] Shin Pan-Seok, Cheung Hee-Jun. A magnetostrictive force and vibration mode analysis of 3kW BLDC motor by a magneto-mechanical coupling formulation[J]. Journal of Electrical Engineering and Technology, 2011, 6(1): 76-80.

[7] Gao Yanhui, Taura Daiki, Nagata Masahide, et al. Loss reduction of reactor with grain-oriented silicon steel plates[J]. IEEE Transactions on Magnetics, 2013, 49(5): 1973-1976.

[8] Yanhui Gao, Masahide Nagata, Kazuhiro Muramatsu, et al. Noise reduction of a three-phase reactor by optimization of gaps between cores considering electromagnetism and magnetostriction[J]. IEEE Transactions on Magnetics, 2011, 47(10): 2772-2775.

[9] Yanhui Gao, Kazuhiro Muramatsu, Muhd Juzail Hatim, et al. Design of a reactor driven by inverter power supply to reduce the noise considering electromagnetism and magnetostriction[J]. IEEE Transactions on Magnetics, 2010, 46(6): 2179-2182.

[10] Jang Pyungwoo, Choi Gwangbo. Acoustic noise characteristics and magnetostriction of Fe-Si powder cores[J]. IEEE Transactions on Magnetics, 2012, 48(4): 1549-1552.

[11] Kitagawa Wataru, Ishihara Yoshiyuki, Todaka Toshiyuki. Analysis of structural deformation and vibration of a transformer core by using magnetic property of magnetostriction [J]. Electrical Engineering in Japan, 2010, 172(1): 19-26.

[12] M Rossi, J Le Besnerais. Vibration reduction of inductors under magnetostrictive and Maxwell forces excitation[J]. IEEE Transactions on Magnetics, 2015, 51(12): 1-7.

[13] 蔡宣三, 高越农(Cai Xuansan, Gao Yuenong). 可控饱和电抗器原理、设计与应用(Fundamentals and applications of controllable saturated reactor)[M]. 北京: 中国水利水电出版社(Beijing: China Water Power Press), 2008.

[14] 颜威利, 杨庆新, 汪友华(Yan Weili, Yang Qingxin, Wang Youhua). 电气工程电磁场数值分析(Numerical analysis of electrical engineering electromagnetic field)[M]. 北京: 机械工业出版社(Beijing: Chain Machine Press), 2005.

[15] 祝丽花, 杨庆新, 闫荣格, 等(Zhu Lihua, Yang Qingxin, Yan Rongge, et al.). 考虑磁致伸缩效应电力变压器振动噪声的研究(Research on vibration and noise of power transformer cores including magnetostriction effects)[J]. 电工技术学报(Transactions of China Electrotechnical Society), 2013, 28(4):1-6, 19.

Analysis on electromagnetic vibration of controllable saturable reactor considering magnetostrictive effects

YANG Yi-mei， ZHU Li-hua， WANG Bin， YANG Qing-xin

(Tianjin Key Laboratory of Advanced Technology of Electrical Engineering and Energy, Tianjin Polytechnic University, Tianjin 300387, China)

Due to its excellent operating characteristics, controllable saturable reactor has been widely used in many kinds of industries, such as power systems and non-ferrous metallurgy. As compensation for electrical equipment, controllable saturable reactor can continuously adjust its reactance and change its capacity. However, due to the special structure and the working characteristics of controllable saturable reactor, vibration and noise of the core are larger. The vibration and noise problem becomes one of the restricting factors of controllable saturable reactor applications. Based on open source model finite element analysis software this paper establishes a magnetic circuit-mechanical coupling model. Considering the electromagnetic and magnetostrictive force numerical analysis of the magnetic field and vibration under different working conditions is completed. The magnetic flux density distribution, core deformation, the magnitude of vibration displacement and vibration acceleration are obtained. The paper provides the theoretical basis and calculation method on the design of reactor to reduce the vibration.

controllable saturable reactor; electromagnetic force; magnetostrictive force (MS); electromagnetic vibration

2015-12-14

国家自然科学基金青年项目(51507110)、国家自然科学基金面上项目(51577131)

杨意妹(1989-)， 女， 河北籍， 硕士研究生， 研究方向为现代工程电磁场与磁技术； 祝丽花(1984-)， 女， 河南籍， 讲师， 博士， 研究方向为现代工程电磁场与磁技术。

TM72

A

1003-3076(2016)08-0040-06