电磁发射装置绝缘支撑结构多场特性研究

李 丹， 徐 蓉， 袁伟群， 严 萍

(1. 中国科学院电工研究所， 北京 100190； 2. 中国科学院大学， 北京 100190； 3. 中国科学院电力电子与电气驱动重点实验室， 北京 100190)

电磁发射装置绝缘支撑结构多场特性研究

李 丹1,2,3， 徐 蓉1,3， 袁伟群1,3， 严 萍1, 3

(1. 中国科学院电工研究所， 北京 100190； 2. 中国科学院大学， 北京 100190； 3. 中国科学院电力电子与电气驱动重点实验室， 北京 100190)

为探究各种因素对绝缘支撑结构性能的影响，基于COMSOL Multiphysics有限元分析软件，通过建立发射装置二维瞬态模型，以麦克斯韦方程、热传导方程、动力学方程作为依据，主要分析绝缘支撑结构的温度和应力分布情况。结果表明，在电磁发射过程中，轨道引起的绝缘支撑结构温升约10K；局部应力最高值远小于绝缘材料的抗张强度。因此，总体上看，轨道对绝缘支撑结构的影响很小。

电磁发射装置； 电流密度； 温度； 应力； 绝缘支撑结构

1 引言

随着电磁发射技术的日趋成熟，其在科学实验、航空航天等诸多领域中扮演越来越重要的角色[1-3]。电磁轨道发射系统利用流经轨道-电枢的电流所产生的磁场与流经电枢的电流之间相互作用的电磁力加速电枢至超高速[4]。在电磁发射运行过程中，存在着电、热和力多场耦合作用[5]。实验中发现发射装置中的绝缘支撑结构破坏频发，尤其在重复发射过程中。由于电磁发射过程复杂，绝缘支撑结构的性能受到多种因素的影响。目前国内外针对绝缘支撑结构绝缘性能的研究涉及较少，早期的研究人员将研究重点放在发射装置绝缘材料的选择和评估[6,7]、使用等离子体电枢发射器时如何减少绝缘侧壁烧蚀的措施[8-10]以及方口径发射器绝缘侧壁的金属沉积[11-13]等方面，在数值计算上主要针对轨道及电枢的瞬态温度分析[14,15]。本文通过对实验用电磁发射装置建立简化二维模型，运用有限元分析方法，仿真计算得到发射装置绝缘支撑结构的电磁场、温度场及应力场多场耦合特性。

2 多场耦合计算

2.1 理论及模型

电磁发射装置横截面二维简化模型如图1所示。发射装置口径尺寸为10mm×10mm；轨道的横截面为矩形，宽20mm，厚为6mm，材料为紫铜；绝缘支撑结构包括两块绝缘压板和两块绝缘支撑板，材料均为玻璃钢，整个装置通过两排预紧螺栓连接并进行预紧。在构建模型时，为了更好地进行磁场计算，在整个模型外围包上圆形空气域。鉴于整个模型结构的对称性，故只选取左上1/4模型进行分析计算，如图2所示。

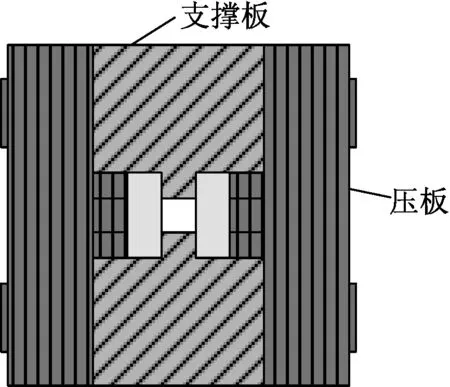
图1 电磁发射装置横截面模型Fig.1 Diagram of electromagnetic launcher cross-section

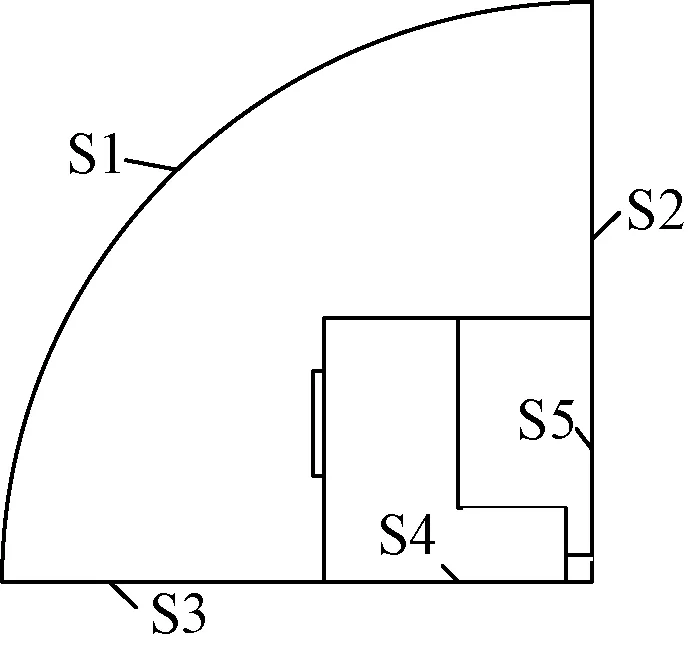
图2 电磁发射装置计算模型Fig.2 Diagram of electromagnetic launcher analyzed

运用有限元方法求解轨道电磁场参数的理论基础是麦克斯韦方程，由麦克斯韦方程推导出A-φ法表示的磁场控制方程[16]为：

φ

(1)

式中，A为磁矢势；φ为标量电位；σ为材料的电导率；μ为材料的磁导率。这里主要考虑二维模型，忽略电枢速度的影响。在求出磁场后，根据场参数之间的关系求得电流密度J与磁感应强度B等参数，再将由电流密度表示的热源Q，导入到热传导方程中，即

(2)

式中，ρ为材料的密度；Cp为定压比热；k为材料的导热系数；T为温度。这里的热源主要考虑电流流过导体产生的焦耳热，由于轨道与绝缘支撑结构相接触，轨道内部电流作用产生的热量通过热传导会对绝缘支撑结构产生影响。同时由电流密度J与磁感应强度B可得载流导体所受的洛仑兹力为：

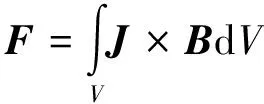
(3)

式中，V为轨道所在积分域。发射装置两轨道由于流过反向的脉冲电流而产生相互排斥的作用力，绝缘支撑结构同时受到轨道电动力和螺栓预紧力的作用，为了得到发射装置各装配结构之间的作用关系，研究绝缘支撑结构瞬态应力分布状态主要基于以结点位移为未知量的运动微分方程[17]：

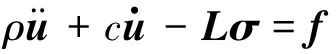
(4)

结合相应的几何方程和本构关系：

ε=LTu

(5)

σ=Dε

(6)

式中，u为位移；ρ为质量密度；c为阻尼系数；f为力载荷；σ为应力；ε为应变；D为弹性矩阵；L为微分算子,其表达式为：

(7)

本文采用有限元软件COMSOL Multiphysics进行求解，在计算时，外围空气域正常网格剖分，而电磁发射装置需要局部加密剖分。

2.2 边界条件设置

在计算磁场时，边界S1可认为无穷远，故设置A=0；边界S2为两轨道对称轴，由于两轨道中电流的大小相等，方向相反，且磁矢势A与电流同向，所以设置A=0；由于磁场与边界S3垂直，所以设置S3为∂A/∂n=0；对于整个计算域A初始值设为零。在热传导模块求解时，对于装置所在边界S4、S5均设为对称边界，整个计算域温度初值设为T=293.15K。在磁场模块中求解电磁力之后，将计算结果作为力载荷导入到固体力学模块实现耦合。在运用结构力学模块计算时，需运用装配体模型分析得出各个部件之间的接触关系，其中装置所在边界S4、S5设为对称边界，螺栓预紧处设为固定约束，整个计算域u的初始值设为零。

在计算时施加在轨道中的脉冲电流波形如图3所示。峰值电流为165kA，脉宽约1ms。计算时所用到各材料物理参数如表1所示。

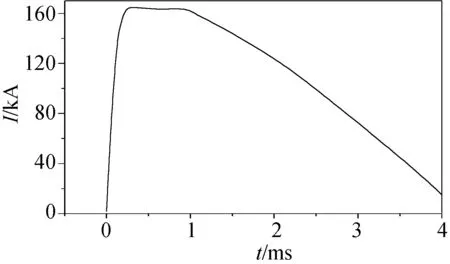
图3 脉冲电流波形Fig.3 Diagram of applied current waveform

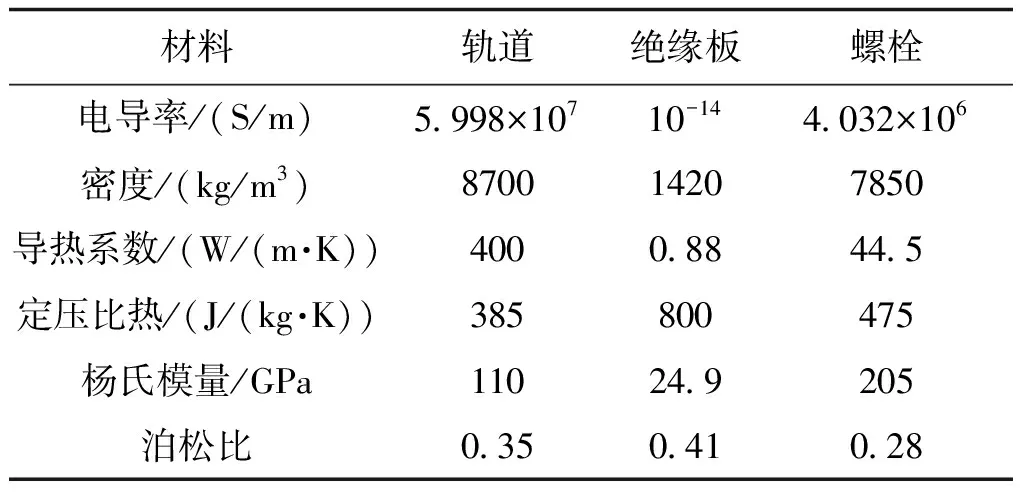
材料轨道绝缘板螺栓电导率/(S/m)5998×10710-144032×106密度/(kg/m3)870014207850导热系数/(W/(m·K))400088445定压比热/(J/(kg·K))385800475杨氏模量/GPa110249205泊松比035041028

3 计算结果及分析

由于轨道的激励电流为脉冲电流，电流大小随时间变化且作用时间极短，所以导体内电流密度的分布会受到趋肤效应的影响而产生不均匀分布。图4为t=0.1ms,0.5ms,1ms时刻的轨道横截面电流密度分布。可以看出瞬态电流在轨道横截面的分布特点。在电流作用初始阶段，电流扩散具有明显的趋肤效应，轨道表面的电流密度高于轨道内部，电流更趋向于集中在轨道右边缘，也就是说趋向于分布在两轨道的内表面边缘。随着时间推移，电流逐渐由轨道表面向轨道内部扩散，以t=1ms时刻为例，轨道电流密度逐渐趋向于均匀分布。

图4 电磁发射不同时刻轨道电流密度分布图Fig.4 Distribution of current density within rails at different times

图5 轨道和局部绝缘板温度分布Fig.5 Distribution of temperature within rails and local insulators

图5为轨道和局部绝缘板表面在t=10ms和1s时的温度分布。可以看出绝缘板的高温区域主要集中在与轨道相接触的表面上，并且从t=10ms到t=1s时刻，轨道的温度逐步趋于均匀分布，而绝缘板的高温仅分布在表面边缘，这是因为与轨道相比，绝缘材料的导热系数极低(轨道和绝缘板的导热系数分别为400W/(m·K)和0.88W/(m·K)，热量在绝缘板中扩散十分缓慢，1s扩散不到1mm。绝缘板的温度范围在295～305K之间，温升大约在10K左右，可知轨道的热效应对绝缘板的影响很小。

图6为绝缘支撑结构1ms时在螺栓预紧力和轨道电动力共同作用下的应力分布和变形情况。从整体上看，绝缘压板受力远大于绝缘支撑板，绝缘支撑板基本不受力，最大应力出现在绝缘压板螺栓预紧内侧，其值为98MPa，远远小于玻璃钢材料的强度极限350MPa，同时绝缘压板拐角处也是相应的高应力区。仿真结果表明，在电磁发射过程中轨道的冲击力并没有对绝缘板产生很大影响。

图6 绝缘支撑结构1ms时von Mises应力分布图Fig.6 Distribution of stress within insulators at 1ms

4 结论

本文通过仿真计算得到发射装置绝缘支撑结构的温度及应力分布特点，发现轨道的热效应及冲击力在电磁发射过程中对绝缘支撑结构的影响很小。在电磁发射实验中发现发射装置膛内过程极其复杂，所以分析引起绝缘板破坏的因素应重点关注电弧烧蚀、金属沉积等一系列膛内主导因素。本文可为后续进一步研究发射装置绝缘破坏提供理论依据。

[1] Fair H D. Electromagnetic launch science and technology in the United States enters a new era[A]. 2004 12th Symposium on Electromagnetic Launch Technology[C]. 2005.1-8.

[2] 王静端(Wang Jingduan).电磁发射技术的发展及其军事应用(The development and application of military electromagnetic emission technology)[J].火力与指挥控制(Fire Control and Command Control),2001,26(1):5-7.

[3] 李立毅,李小鹏(Li Liyi, Li Xiaopeng).电磁发射的历史及发展趋势(History and development trend of electromagnetic launch)[J].微电机(Micromotors), 2004, 37(1):41-44.

[4] Ghassemi M, Pasandeh R. Thermal and electromagnetic analysis of an electromagnetic launcher[J]. IEEE Transactions on Magnetics, 2003, 39(3):1819-1822.

[5] 张保玉,黄伟,陈子明,等(Zhang Baoyu, Huang Wei, Chen Ziming, et al.). 高速滑动电接触下轨道槽蚀损伤问题研究(Grooving damage of rails under high-velocity sliding electrical contact)[J]. 兵器材料科学与工程(Ordnance Material Science and Engineering),2015,(3):140-143.

[6] Olsen R, Chamberlain F, Mcclung J. Railgun insulator materials test[J]. IEEE Transactions on Magnetics, 1986, 22(6):1628-1632.

[7] Rosenwasser S, Stevenson R. Selection and evaluation of insulator materials for high performance railgun bores[J]. IEEE Transactions on Magnetics, 1986, 22(6):1722-1729.

[8] Wetz D, McNab I, Stefani F, et al. Developments in making space access rapid and affordable using a plasma railgun[A]. IEEE Pulsed Power Conference (PPC’09)[C]. 2009.742-746.

[9] Stefani F, McNab I R, Parker J V, et al. A plasma railgun experiment addressing launch-to-space issues[J]. IEEE Transactions on Magnetics, 2007,43(1): 194-197.

[10] Zielinski A E, Werst M D. Cannon-caliber electromagnetic launcher[J]. IEEE Transactions on Magnetics, 1997, 33(1): 630-635.

[11] Watt T, Motes D T. The effects of surface coatings on the onset of rail gouging[J]. IEEE Transactions on Plasma Science, 2011, 39(1):168-173.

[12] Gee R M, Persad C. Multishot performance of an insulator in a laboratory electromagnetic launcher[J]. IEEE Transactions on Magnetics, 2001, 37(1):257-262.

[13] Wetz D A, Watt T J, Surls D, et al. Investigation into the behavior of armature ejecta in electromagnetic launchers[J]. IEEE Transactions on Plasma Science, 2011, 39(3):947-952.

[14] Vanicek H, Satapathy S. Thermal characteristics of a laboratory electromagnetic launcher[J]. IEEE Transactions on Magnetics, 2005,41(1):251-255.

[15] 曹昭君,肖铮(Cao Zhaojun, Xiao Zheng).电磁发射系统C型固体电枢的电流密度分布特性及其机理分析(Current density distribution characters of C-shaped armature in EML system)[J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2012, 31(2): 23-26.

[16] Hsieh K. A Lagrangian formulation for mechanically, thermally coupled electromagnetic diffusive processes with moving conductors[J]. IEEE Transactions on Magnetics, 1995, 31(1): 604-609.

[17] 尹冬梅, 栗保明(Yin Dongmei, Li Baoming). 基于接触算法的电磁轨道发射装置的磁场-结构耦合数值分析(Numerical analysis of magnetic-structural coupling for electromagnetic rail launcher based on contact algorithm)[J]. 高压物理学报(High Pressure Physics), 2013, (5):757-762.

Study on multi-physics characteristics of insulators in electromagnetic launcher system

LI Dan1,2,3, XU Rong1,3, YUAN Wei-qun1,3, YAN Ping1,3

(1. Institute of Electrical Engineering, Chinese Academy of Sciences, Beijing 100190, China; 2. University of Chinese Academy of Science, Beijing 100190, China; 3. Key Laboratory of Power Electronics and Power Drives, Chinese Academy of Sciences, Beijing 100190, China)

To explore different influence factors which caused insulation performance degradation, we established a two dimensional transient electromagnetic launcher model on the basis of finite element software COMSOL Multiphysics. According to Maxwell equations, thermal diffusion equation and transient dynamics equations, we obtain temperature distribution and stress distribution within the insulators. From the overall results, the temperature-rise generated by rails within the insulators is small. And local stress maximum is much less than the tensile strength of insulation materials. In general, rails have the least influence on insulators breakdown in electromagnetic launcher system. This work will provide a basis for further research on insulators performance in the process of electromagnetic launch.

electromagnetic launcher; current density; temperature; stress; insulators

2016-01-04

国家自然科学基金(51237007； 51207035)资助项目

李 丹(1990-)， 女， 天津籍， 硕士研究生， 研究方向为高电压与绝缘技术； 徐 蓉(1981-)， 女， 甘肃籍， 副研究员， 博士， 研究方向为脉冲功率技术。

TM153；TM215.92

A

1003-3076(2016)08-0036-04