一种板球系统的Box-Jenkins模型辨识研究

夏泽雨，崔世钢，耿立辉

（天津职业技术师范大学天津市信息传感与智能控制重点实验室，天津　300222）

上述的准则函数可以写为：



一种板球系统的Box-Jenkins模型辨识研究

夏泽雨，崔世钢，耿立辉

（天津职业技术师范大学天津市信息传感与智能控制重点实验室，天津300222）

摘要：板球系统是一种典型的非线性多变量系统，是先进控制理论、系统辨识和状态估计等方法的典型验证平台，其主要功能是让小球在平板上按照期望的轨迹运行。由于机器老化，先前的机理模型已不能表示板球系统的动态特性。为保证控制精度，为板球系统后期先进控制器的设计提供模型依据，本文将已有的关于离散系统的Box-Jenkins模型辨识技术，推广应用到连续时间板球系统的模型中，利用参考输入信号的方法设计出持续激励作为输入信号，采用辅助变量法和最小二乘法来分别辨识板球系统模型和噪声模型，利用双线性变换得出板球系统的连续时间Box-Jenkins模型，通过数值仿真实例，验证了这种方法的有效性。

关键词：板球系统；Box-Jenkins模型；辅助变量法；最小二乘法

板球系统是球杆系统的二维扩展。作为具有2个自由度的机械系统，板球系统通常用于对动态系统的研究和在实验室进行经典控制理论和现代控制理论的控制过程研究，是先进控制理论、系统辨识和状态估计等方法的典型验证平台。其控制对象是具有2个相互垂直的旋转轴的板，目的是让一个自由滚动的小球能够平衡在平板上特定的位置，或沿一定的轨迹滚动。板球系统涉及自动控制、运动控制、数字图像处理、机器视觉等领域[1]。由于系统长期使用，机器老化，系统存在误差，先前的机理模型已不能准确描述系统的真实模型。为给板球系统设计出更高精度的控制器，需要采集实时实验数据以辨识出板球系统的真实模型。

早在20世纪20年代，研究人员就开始研究B-Jenkins模型，直到1970年George Box和Gwilym Jenkins[2]提出著名的时间序列预测模型，也就是Box-Jenkins模型。该模型是指将非平稳时间序列转化为平稳时间序列，然后将因变量仅对其滞后值及随机误差项的现值和滞后值进行回归所建立的模型。研究发现，关于板球系统的辨识非常少，先前的Box-Jenkins模型辨识技术只能应用到离散时间系统上，而本文将该方法推广应用到连续时间板球系统的模型辨识中。本文利用Box-Jenkins模型辨识板球系统的系统模型和噪声模型，为板球系统后期的先进控制器设计提供模型依据。首先为板球系统闭环控制系统设计出合适的M序列，之后利用辅助变量法和最小二乘法估计出板球系统的Box-Jenkins模型[3]，最后通过双线性变换和最小实现处理得到板球系统理想的实时模型。

1　板球系统的数学模型

对板球系统而言，如果仅采用力学方法，板球系统的数学模型将很难得到。拉格朗日法在机器人建模中的成功应用说明它比较适合解决这种复杂的机械系统问题，因此采用拉格朗日方法来计算推导板球系统的数学模型。拉格朗日方程的一般形式为：

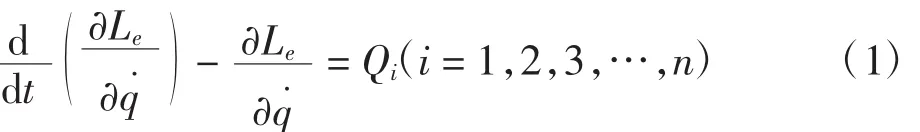
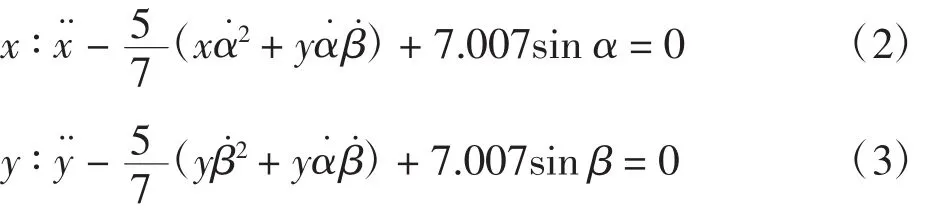
小球在x轴的运动可以被描述成如下的线性状态空间方程组[1]

这个等式中输入、输出矩阵为：

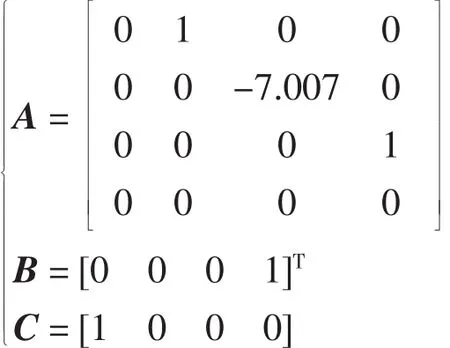
因而，板球系统上关于小球在x轴上和平板在x轴上的角加速度数学模型可以计算出来，数学模型为：

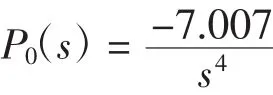
由上式可知，板球系统的数学模型是一个4阶系统。

2　基于BJ模型的辨识方法

实际过程中，干扰大部分都是有色噪声，这类模型可以表示为Box-Jenkins模型，它可以描述为[4-5]：

式中：A（z-1）= 1 + a1（z-1）+ anaz-na；B（z-1）= 1 + b1（z-1）+ bnbz-nb；C（z-1）= 1 + c1（z-1）+ cncz-nc；D（z-1）= 1 + d1（z-1）+ dndz-nd；u（k）和y（k）分别表示系统模型的输入和被噪声污染的输出；v（k）表示不相关的零均值白噪声。

2.1系统模型的辨识

在板球系统中，首先关注如下描述形式的板球系统模型的辨识问题。

对于噪声模型部分，令

则线性动态模型系统可以表述为：

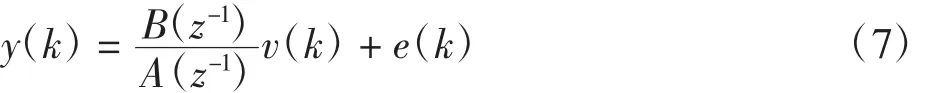
式中：u（k）和y（k）为模型系统的输入变量和输出变量；e（k）为有色噪声。由于直接用最小二乘法不能得到模型参数的无偏、有效估计，因而式（7）可以写成最小二乘的形式

式（8）中

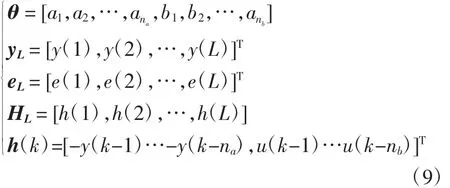
式中：L为数据长度；na和nb分别为多项式A（z-1）和B（z-1）的阶次。

为获得模型参数的无偏、一致估计，设模型残差为：

上述的准则函数可以写为：

参考文献在[3]中证明出式（12）收敛的条件。所谓的收敛，就是是从输入、输出数据集合中构造出来的向量，称之为辅助变量。该变量可以选择多种形式([3])，本文列出下面一种形式

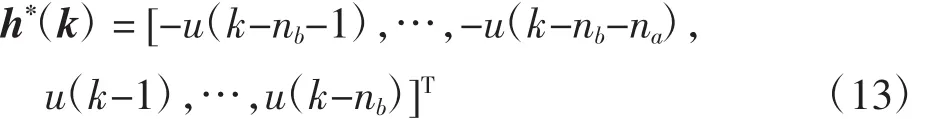
式中：滞后nb步的输入u（k - nb- i）（i = 1，2，…，na）为辅助变量。

由h*（k）组成的H*L可称作辅助矩阵。通过上述分析可知，式（13）能够估计出Box-Jenkins模型的系统模型部分。

2.2噪声模型部分辨识

对于噪声模型部分，令

式中：v（k）为输入；eˆ（k）为输出。现在问题就变为ARMA模型的参数辨识问题，将式（14）经过如下的转换得到

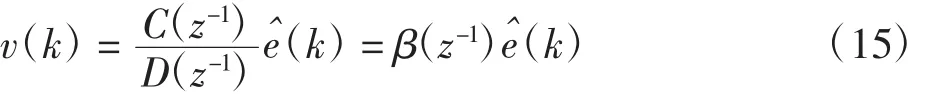
式（15）有最小二乘法结构为：

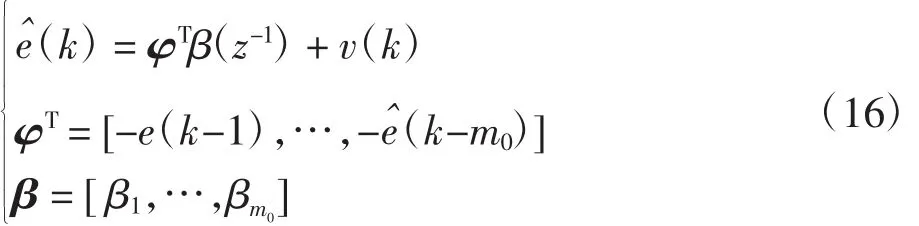
可以得到β的估计值，进而可以推算出v（k）的估计值。

应用高阶AR模型，可将式（14）转化为如下ARX模型结构

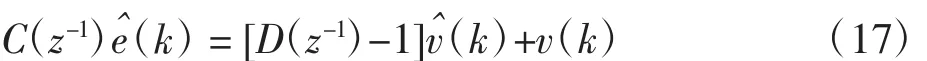
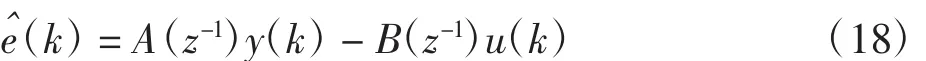
由最小二乘法（LS）就能够估计出C（z-1）和D（z-1）。

3　板球系统的辨识

3.1辨识思路

一般的板球控制系统如图1所示。图1中：K（z-1）为控制器；P（s）为板球系统；u0和ym为在辨识中采集到的实验数据，分别是系统的输入和噪声污染的输出；v（k）为噪声。

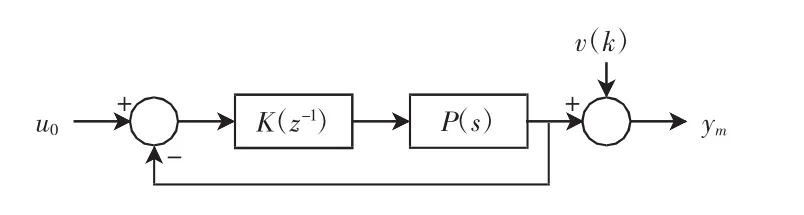
图1　板球控制系统方框图

根据上文的辨识算法就能够辨识出板球系统的模型，辨识的过程如图2所示。

根据信号的流动关系可以得到这个闭环系统的模型为[6-7]：

图2中，由式（19）完成Guy（z-1）到P（z-1）的转化，即得到板球系统的离散模型为：

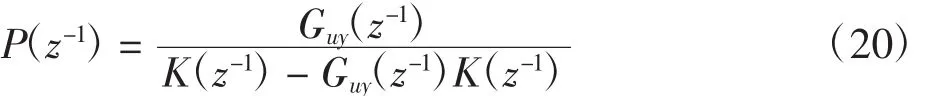
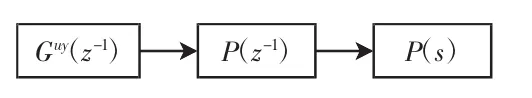
图2　辨识过程

应用如下双线性变换，完成P（z-1）到P（s）的转换，即可得到板球系统的连续系统为：

式中：T为采样时间。

3.2参考输入信号的设计

连续时间的伪随机二值信号（PRBS）又名M序列，是周期的确定信号，且可复现。故可设计M序列作为板球实验控制系统的参考输入信号，其设计方法和步骤如下。

（1）在稳定控制系统的输入端加上脉冲信号，观察脉冲信号从加入到输出减少为最高脉冲响应10%所经历的时间，该时间就为过渡过程时间Ts。

（2）在参考信号的输入端加上占空比为50%的方波信号，逐渐增加该信号的频率，直到输入信号没有明显的变动位置，该时刻信号的频率即为最高截止频率fmax。

（3）利用过渡过程时间Ts和最高截止频率fmax来确定M序列的参数，确定的规则为：

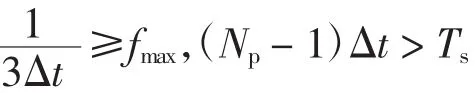
式中：Δt为脉冲间隔；Np为周期数。

3.3辨识步骤

步骤1确定u0。通常情况下，M序列具有白噪声的特性，比较容易实现，故M序列可被当作输入信号。根据上文所述参考输入信号的设计方法可以确定合适的M序列。

步骤2对采集到的u0和ym做预处理，创造一个数据对象。

步骤3对该数据对象采用Box-Jenkins辨识方法进行辨识，得到系统的Box-Jenkins模型，根据式（19）和式（20）可以推算出板球系统的离散模型。

步骤4根据式（21），将得到的离散数学模型进行转换，得到板球系统的连续模型。

4　仿真验证

前期研究中，已经设计好H∞回路成形鲁棒控制器，其离散形式结构为[8-10]：

式中：P（s）为板球系统的数学模型。根据3.2提出的设计M序列的方法，得出过渡过程时间Ts= 0.035 s和最高工作频率fmax= 2 Hz，设计出如下的M序列为：

以此PRBS作为持续输入激励u0，噪声为均值0、方差为0.001的高斯白噪声，采样时间T = 0.03 s，数据长度为1 667，对采集到的数据进行Box-Jenkins模型辨识方法，得到离散的辨识模型，将其进行双线性变换，得到的板球系统的辨识模型表达式为：

噪声模型可以表示为：

辨识的模型和板球系统真实模型的伯德图如图3所示。由图3可以看到：在中频段的吻合效果比较好；在低频段和高频段吻合效果比较差，但是板球系统的控制器设计中，中频段的辨识精度至关重要。辨识的模型和板球系统真实模型控制系统正弦响应的对比图如图4所示，由图4可知辨识的效果令人满意。

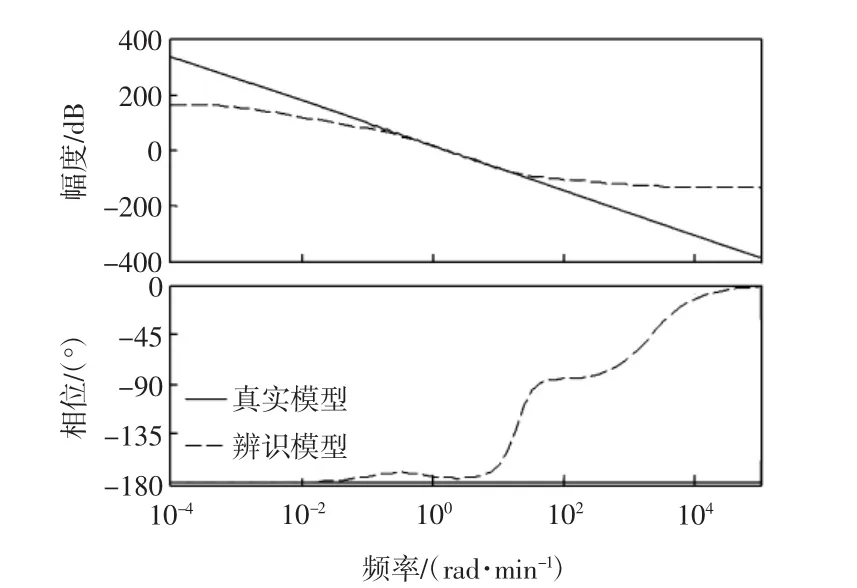
图3　伯德图对比

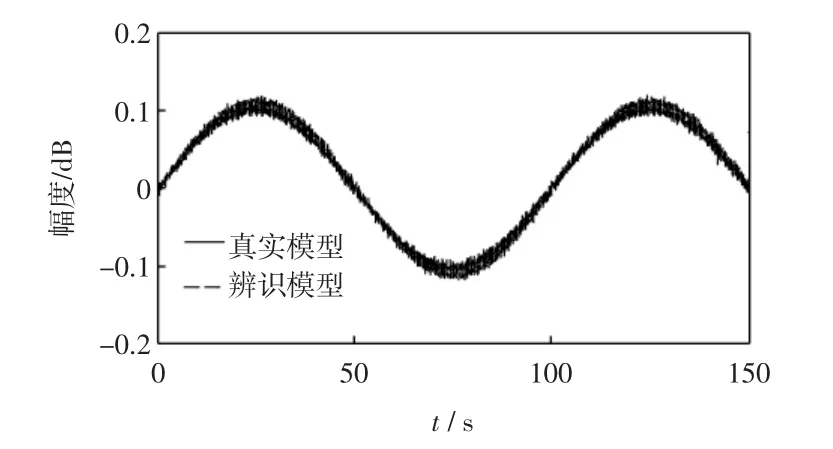
图4　正弦响应对比

5　结束语

在已有离散系统Box-Jenkins模型的基础上，首先辨识出板球系统的闭环模型，通过转化得到板球系统的离散模型，之后通过双线性变换得到板球系统的连续模型，辨识的效果令人满意，辨识出的板球系统模型为板球系统后期的先进控制器设计提供模型依据。由于在实际工业中，系统模型多为变量带误差模型，因此在今后的研究中，还应更多地关注板球系统变量带误差模型的辩识。

［1］深圳元创兴科技有限公司.深圳板球系统实验指导书［Z］.深圳：深圳元创兴科技有限公司，2011.

［2］LENNART L.System Identification：Theory for the User［M］.New Jersey：Prentice Hall，1999.

［3］萧德云，方崇智.系统辨识理论及应用［M］.北京:清华大学出版社，2014.

［4］杨慧中，张勇.Box-Jenkins模型偏差补偿方法与其他辨识方法的比较［J］.控制理论与应用，2007，24（2）：215-222.

［5］丁锋.辨识Box-Jenkins模型参数的递推广义增广最小二乘法［J］.控制与决策，1990，16（6）：53-56.

［6］胡寿松.自动控制原理［M］.北京：科学出版社，2007.

［7］GENG L H，XIAO D Y，ZHANG T，et al.Worst-case identification of errors-in-variables models in closed loop［J］.IEEE Transactions on Automatic Control，2011，56（4）：762-771

［8］林海奇.一种板球系统的H∞回路成形鲁棒镇定控制器设计研究［D］.天津：天津职业技术师范大学，2015.

［9］LIN H Q，CUI S G，GENG L H，et al.H∞robust controller design for a ball and plate system using normalized coprime factors［C］//26th Chinese Control and Decision Conference.2014：357-362.

［10］耿立辉，田立国，段海龙，等.连续时间变量带误差系统的辨识方法研究［J］.天津职业技术师范大学学报，2012，22 （4）：1-4.

欢迎订阅《天津职业技术师范大学学报》

《天津职业技术师范大学学报》是天津职业技术师范大学主办的面向国内外公开发行的综合性学术刊物，刊号CN 12－1423/Z，ISSN 2095-0926。

本刊为季刊，每册定价5.00元，全年4期共计20.00元，邮局订阅，邮发代号6－193。

邮政编码：300222联系电话：（022）28111205

E－mail：LLBXB@126.com

本刊网址：http：//xuebao.tute.edu.cn/xbsy.htm.

Identification on a Box-Jenkins model for a ball and plate system

XIA Ze-yu，CUI Shi-gang，GENG Li-hui
（Tianjin Key Laboratory of Information Sensing & Intelligent Control，Tianjin University of Technology and Education，Tianjin 300222，China）

Abstract：A ball and plate system is a kind of typical and nonlinear system，which is also a multi- input and multi-output （MIMO）system.A ball and plate system is a typical test platform for advanced control theory，system identification，state estimation method and so on，and its main function is to make the ball run according to the desired trajectory on the plate.Because of the existence of the machine′s friction and aging，the mechanism of the previous model cannot express the true model of a ball and plate system.In order to ensure the control precision，and provide the cricket system for later advanced controller design，according to the model，the existing discrete system on the Box-Jenkins model identification technology is applied and popularized to continuous time cricket system model，the reference input signal is used to design sustained excitation as the input signal，and the instrumental variable method and least square method are used to estimate the cricket system model and noise model.By using bi-linear transform that cricket system of continuous time Box-Jenkins model，a numerical simulation example is given to verify the validity.

Key words：ball and plate system；Box-Jenkins model；instrumental variable method；least squares method

通讯地址：天津市河西区大沽南路1310号《天津职业技术师范大学学报》编辑部

作者简介：夏泽雨（1988—），男，硕士研究生；崔世钢（1963—），男，教授，博士，硕士生导师，研究方向为机器人控制、人工智能等.

基金项目：国家自然科学基金资助项目（61203119）；天津市自然科学基金重点项目（14JCZDJC36300）；天津市高等学校科技发展基金资助项目（20130824）；天津职业技术师范大学科研发展基金资助项目（RC14-48，KYQD03010）.

收稿日期：2016-01-26

中图分类号：TP273

文献标识码：A

文章编号：2095－0926（2016）01－0001－05