卡尔曼滤波和最小二乘法结合的机动目标轨迹仿真

王　辂，郑宏兴，邓东民，万小凤

（天津职业技术师范大学天线与微波技术研究所，天津300222）



卡尔曼滤波和最小二乘法结合的机动目标轨迹仿真

王辂，郑宏兴，邓东民，万小凤

（天津职业技术师范大学天线与微波技术研究所，天津300222）

摘要：为有效处理雷达系统采集的机动目标数据，利用旋转矩阵建立地球坐标系与雷达坐标系之间的转换关系，将卡尔曼滤波法与最小二乘法相结合，得到实时可靠的目标运动轨迹。应用数据关联算法，准确分离单个雷达测量的不同机动目标信息，分别得到每个目标的轨迹曲线及运动状态，实现对目标的实时监测。

关键词：旋转矩阵；卡尔曼滤波；最小二乘法；数据关联算法

目标跟踪是根据雷达等设备所获得对目标的测量信息，连续对目标的运动状态进行估计[1-2]，进而获取目标的运动态势及意图。目标机动是指目标的速度大小和方向在短时间内发生变化，通常采用加速度作为衡量指标。前者需要通过调整自身的运动状态和雷达的跟踪状态，避免丢失跟踪目标；后者则通过做规避的机动动作或者释放干扰信号，尽快摆脱跟踪。

卡尔曼滤波器[3-4]是一种用于时变系统的递归滤波器。在雷达系统中，目标的位置、速度和加速度的测量值都有噪声，卡尔曼滤波器能有效滤除噪声带来的影响，得到一个关于目标位置较为准确的估计。本文通过建立雷达与机动目标的空间坐标关系，将卡尔曼滤波和最小二乘拟合法有效结合起来，得到目标的状态信息。利用数据关联算法，合理分离单个雷达探测到的2个目标信息，获得2个目标各自的运动轨迹。

1　卡尔曼滤波的原理

卡尔曼滤波是一套基于状态空间的递推滤波算法[5]，其模型包括状态空间模型和观测模型[6]。前者通过状态方程来描写相邻时刻的状态转移变化规律，后者则反映了实际观测量与状态变量之间的关系。滤波问题就是结合观测信息及状态转移规律来得到系统状态的最优估计[7-8]。假设动态系统的状态空间模型为：

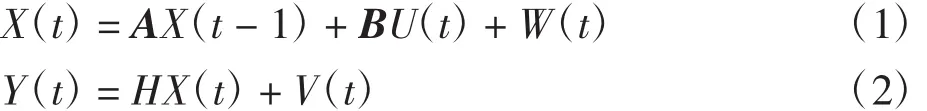
式中：X（t）为系统在时刻t的状态，其协方差阵为P；A 和B是系统参数，对于多模型系统，它们为矩阵；U（t）是t时刻对系统的控制量，若没有控制量，U（t）= 0；W（t）为过程噪声，其协方差阵为Q；Y（t）是对状态的测量值；H为测量系统的参数；V（t）为测量噪声，其协方差阵为R。根据式（1）和式（2），可得到计算流程如下。

a.基于t - 1时刻状态预测t时刻状态：

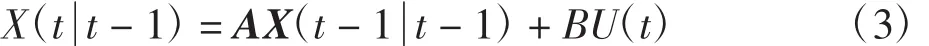
b.计算t时刻状态协方差预测值：

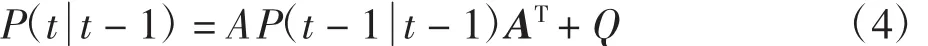
c.结合测量值计算t时刻最优预测值：

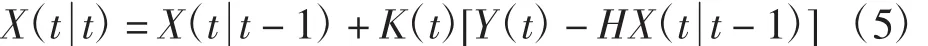
d.计算卡尔曼滤波增益：

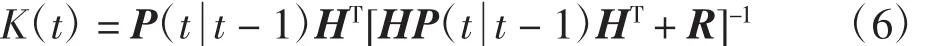
e.计算t时刻状态协方差最优预测值：

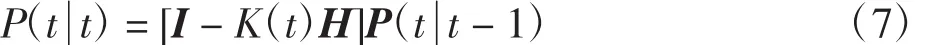
式（7）中：I为单位矩阵。由式（3）到式（7）地不断循环，可以通过最新的测量值持续预测出下一状态。

2　坐标系变换

2.1地球坐标系

假设地球近似为半径等于Re的正球体，地球坐标系OXYZ是以地球质心为原点O的直角坐标系。其中，Z轴从原点O指向地球的正北极；X轴从原点O指向赤道面与格林尼治子午圈的交点；Y轴在赤道平面内。地球坐标系、雷达坐标系及位置关系如图1所示，其中X轴、Y轴和Z轴成正交关系，并符合右手法则，如图1（a）所示。

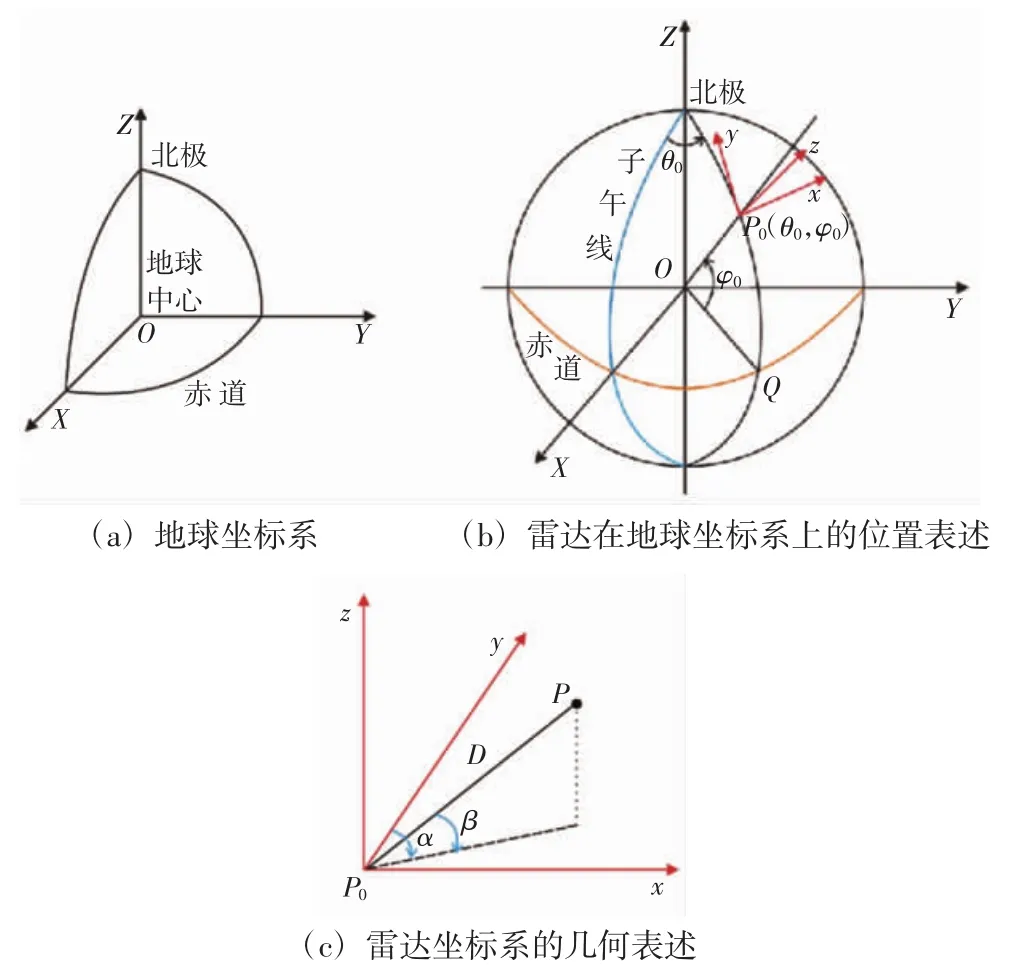
图1　地球坐标系、雷达坐标系及其位置关系示意图

2.2雷达坐标系

假设雷达坐标系P0xyz是以雷达所在位置P0为坐标中心的直角坐标系。x轴沿P0点所在纬线的切线方向指向东；y轴沿P0点所在经线的切线方向指向北；地心与P0点的连线指向天的方向为z轴，如图1（b）。

被测目标的所在位置为P点；方位角α是y轴与P点在xP0y平面投影的夹角，范围为0°～360°；俯仰角β是雷达与被测目标连线PP0与xP0y平面的夹角，范围为-90°～90°，其中PP0= D，如图1（c）所示。

2.3雷达坐标系和地球坐标系的转化

雷达在测量时以雷达坐标系为基准，由于每个雷达坐标系之间均有差异，当涉及多个雷达数据时，就需要将每个目标都转化到地球坐标系上再进行分析。由图1（b）和图1（c）可以得到雷达在地球坐标系上的位置表述，θ0和φ0分别表示地球坐标系上的经度值和纬度值，点P0的坐标写为：

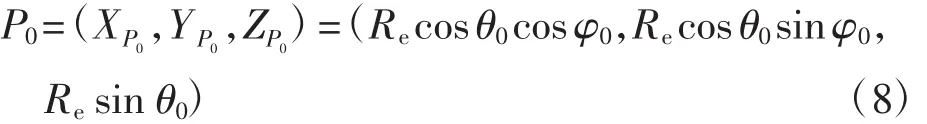
此时，引入旋转矩阵，可将雷达坐标系变换为地球坐标系。当雷达坐标系上的点（x，y，z）分别绕地球坐标系的X、Y、Z轴旋转时，旋转矩阵为：

地球坐标系到雷达坐标系的总旋转矩阵为：

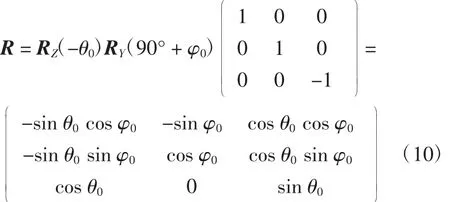
假设地球坐标系上某一点为（Xg，Yg，Zg），它从地球坐标系到雷达坐标系上的点（xg，yg，zg）转换关系为：得到雷达坐标系到地球坐标系上的点（Xg，Yg，Zg）转换关系为：

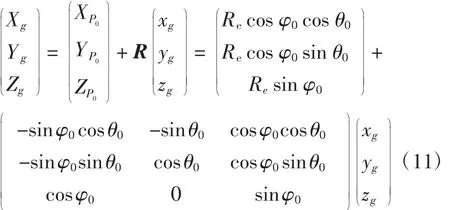
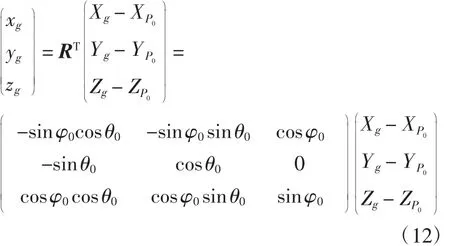
考虑雷达对目标进行探测时，可得到距离D、方位角α、俯仰角β及相应时刻等物理量，因此由图1（c）可得：

3　多雷达对单目标的追踪

由处在地球上不同位置的3个雷达分别记录不同时刻与机动目标的距离、方位角度和俯仰角度等信息，通过坐标变换关系得到被测目标的雷达测量轨迹如图2所示。图2描绘了从36620.4s到36874.4 s内机动目标在地球坐标系下的位置变化情况。

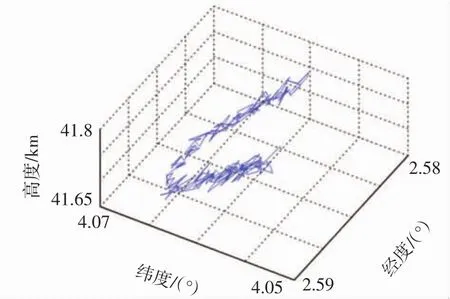
图2　被测目标的雷达测量轨迹

由图2可知，雷达直接获取的信息是变动很大的值，难以对被测目标的具体位置做出准确的判断。此时，采用卡尔曼滤波法，滤除信息中的高频杂量，得到较为平滑的运动轨迹，能够实时确定被测目标的位置，被测目标的拟合轨迹如图3所示。图3（a）为卡尔曼滤波轨迹，经卡尔曼滤波后的轨迹仍有欠缺。再采用最小二乘法，对得到的轨迹进行曲线拟合处理，可得到更加光滑的轨迹曲线，以便对目标轨迹做出规律性判断，如图3（b）所示。

拟合后的轨迹曲线是一个关于时间t的函数。与卡尔曼滤波后的结果及雷达探测结果对比可知，拟合曲线更加符合被测目标的运动轨迹要求。如果将结果分解到X、Y、Z 3个方向上，对时间t求2次导数便可得到被测目标的速度v（t）和加速度a（t）。

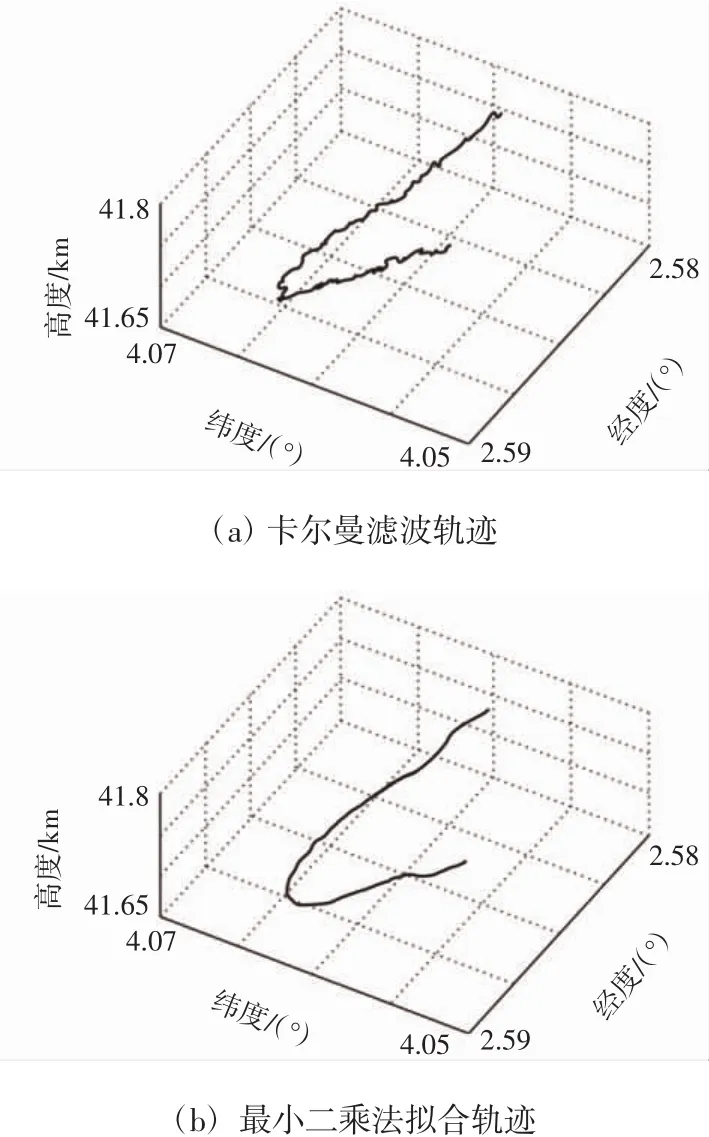
图3　被测目标的卡尔曼滤波和最小二乘法拟合轨迹

4　单雷达对多目标的追踪

为进一步说明这种方法对多目标跟踪的效果，以一个雷达对2个机动目标的追踪数据为例，在雷达坐标系上，对各参数进行相应的数据关联分析，按要求分离2个被测目标的轨迹。雷达在单个时间点上仅有一个回波点迹，需要采用一种有效的分离方法来处理数据，从而还原被测目标的轨迹。本文采用联合概率数据关联算法，建立一个结果与多个目标之间的关联假设，并以关联概率为权值求取测量波门内的有效观测融合值，作为等效测量对目标轨迹进行更新。利用这种方法可以有效还原出“飞行包线”。单一雷达探测双目标的“飞行包线”如图4所示。

应用第3节的方法得到的结果如图5所示，2条曲线分别表示2个目标的运动轨迹。这样，可以很好地描绘出2个被测目标在空中的运动轨迹。雷达在扫描过程中，一个时间点上只有一个回波点迹，需要根据仅有的一个回波点迹，同时保持2个被测目标在时间、位置、速度和加速度的相对连续性，并进行逐点实时筛选，才能有效分离2个目标的轨迹，并且保证轨迹不丢失。由图4和图5可知，利用数据关联算法分离单个雷达检测到2个目标的数据是有效的。

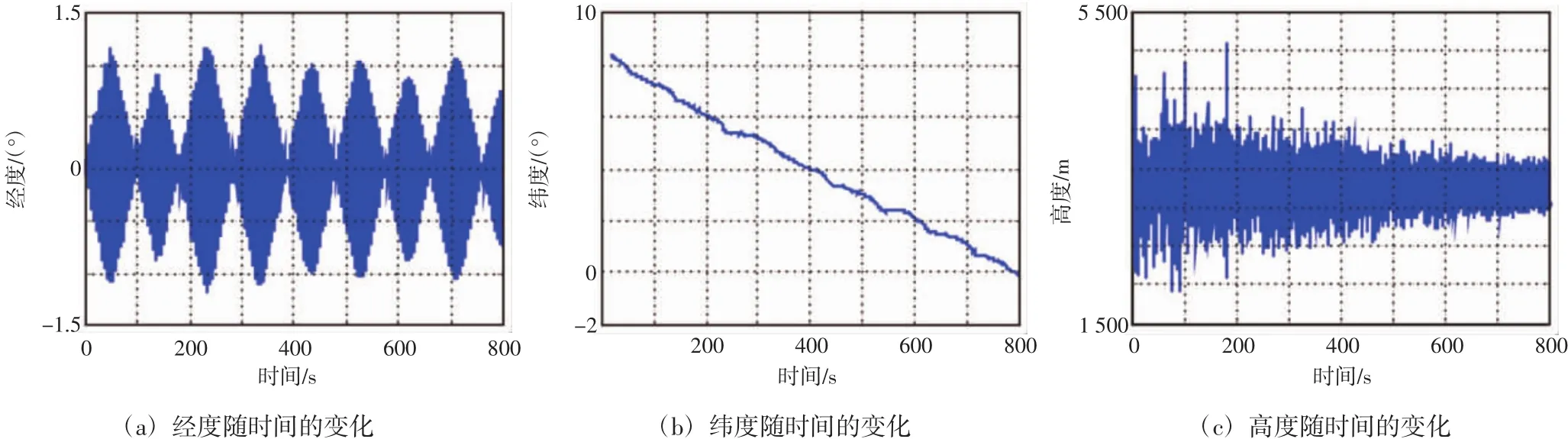
图4　单一雷达探测双目标的经度、纬度和高度随时间的变化

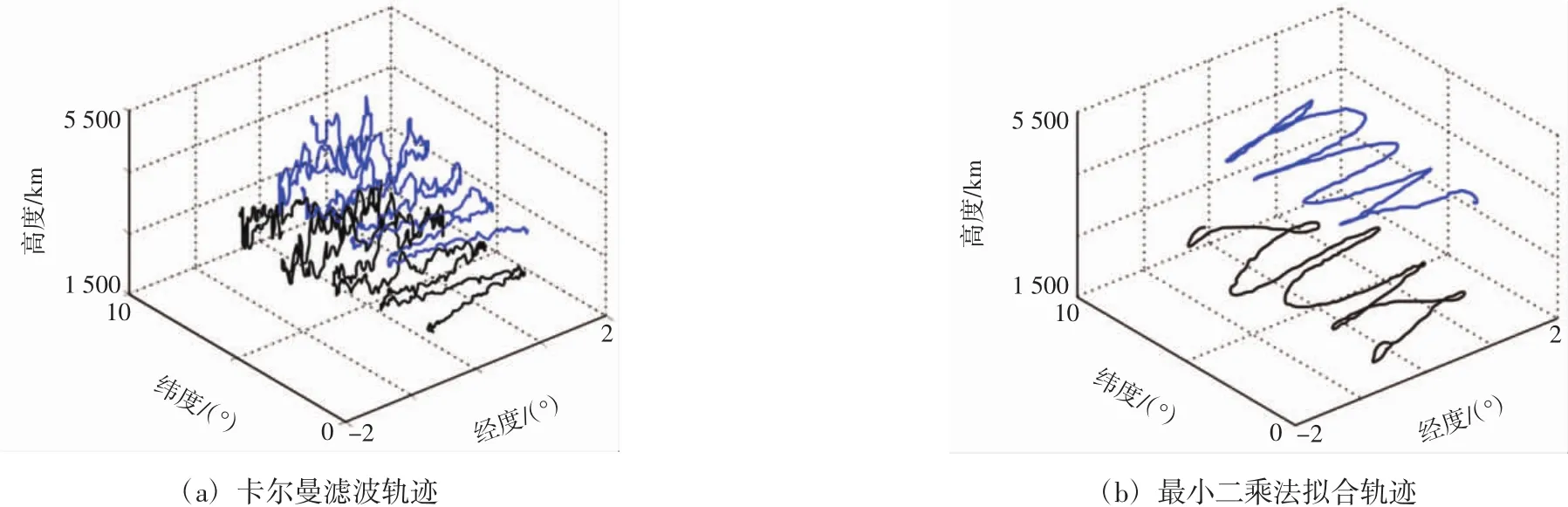
图5　单一雷达探测双目标的卡尔曼滤波和最小二乘法拟合轨迹

5　结束语

建立地球坐标系与雷达坐标系之间的关系，能够有效还原雷达的监测信息。通过卡尔曼滤波与最小二乘拟合相结合的方法，可以得到被测目标的状态以及其速度和加速度等状态信息。利用多目标跟踪的联合概率数据关联算法，有效将单个雷达探测到的2个未知目标分开，通过数据分析确定2个目标的运动状态。虽然受到一些因素的限制，但目标机动在战术上具有主动优势，机动目标跟踪也将成为今后跟踪理论研究的热点和难点。

参考文献：

［1］杨柳.改进卡尔曼滤波的目标跟踪研究[J].计算机仿真，2010，27（9）：351-355.

［2］王建华，张琳.基于改进卡尔曼滤波方法的机动目标跟踪研究[J].现代防御技术，2006，34（2）：16-19.

［3］虞旦，韦巍，张远辉.一种基于卡尔曼预测的动态目标跟踪算法研究[J].光电工程，2009，36（1）：52-56.

［4］敬喜.卡尔曼滤波器及其应用基础[M].北京：国防工业出版社，1973.

［5］孙凯，刘士荣.多目标跟踪的改进Camshift/卡尔曼滤波组合算法[J].信息与控制，2009，38（1）：9-14.

［6］王学斌，徐建宏，张章.卡尔曼滤波器参数分析与应用方法研究[J].计算机应用与软件，2012，29（6）：212-215.

［7］郑润高，张安清.雷达机动目标跟踪的卡尔曼粒子滤波算法[J].电光与控制，2012，19（1）：50-53.

［8］刘士龙.基于卡尔曼滤波器的非合作目标飞行器视觉追踪[D].北京：北京理工大学，2014.

Simulation for maneuvering target trajectory based on Kalman filter and least square methods

WANG Lu，ZHENG Hong-xing，DENG Dong-min，WAN Xiao-feng
（Institute of Antenna and Microwave Techniques，Tianjin University of Technology and Education，Tianjin 300222，China）

Abstract：In order to process the data collected by radar system from maneuvering target effectively，a conversion relation between the earth and radar coordinate systems is set up by using rotation matrix.By combining Kalman filtering method with least square method，a real-time and reliable target trajectory has been obtained.Two different maneuvering target′s information measured by single radar has been separated accurately by using data association algorithm.Trajectory curve and motion state of each target is obtained.These methods are convenient for real-time monitoring of targets.

Key words：rotation matrix；Kalman filtering；least square method；data association algorithm

作者简介：王辂（1992—），男，硕士研究生；郑宏兴（1962—），男，教授，博士，硕士生导师，研究方向为天线、微波电路及计算电磁学.

基金项目：国家自然科学基金资助项目（61371043）.

收稿日期：2015-07-06

中图分类号：TN953

文献标识码：A

文章编号：2095－0926（2016）01－0010－04