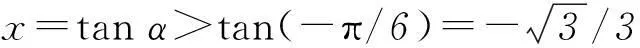自主招生中的常用解题策略



自主招生中的常用解题策略

◇河北李泓序

自主招生作为高校选拔的有益补充越来越受到社会的广泛关注.笔者在学习备考的过程中,对自主招生试题中的一些常用解题策略做如下研究与归纳,在此与读者共享.

1观察、归纳与猜想

分析首先,当m=1时,n2=1,所以n=1;当m=2时,n2=3矛盾;当m=3时,n2=9,所以n=3;当m=4时,n2=33矛盾;当m≥5时,m!是10的倍数.

简证设n=10x+i,x∈N,i∈{1,2,3,4,5,6,7,8,9,10},经计算知n2的个位数只能为0,1,4,5,6,9;最后分析右边,当m≥5时1!+2!+3!+…+m!的个位数为3,故矛盾.

故满足条件的正整数对(m,n)=(1,1)或(3,3)．

2变量代换法

sinα+cos2α-sin2α=sinα+1-2sin2α>0.

所以2sin2α-sinα-1<0，-1/2

(1) 求an;(2) 求证: 2n+1·an<7.

3变更主元

xk2+(2x2+9)k+x3+27=

xk2+(2x2+9)k+(x+3)(x2-3x+9)=

[k+(x+3)][kx+(x2-3x+9)].

所以x1=-k-3或x2+(k-3)x+9=0.

Δ=(k-3)2-36=k2-6k-27=

k(k-6)-27≥9×3-27=0.

综上原方程的解为x1=-k-3,

4逆向思维

(x3+6x-3)2=2(3x2+2)2,

x6-6x4-6x3+12x2-36x+1=0.

令f(x)=x6-6x4-6x3+12x2-36x+1即可．

当然除了本文列举的几种常用策略,还有一些与高考联系特别紧密的方法，在此不再一一列举了,希望能对大家的自主招生及高考有所帮助.

(作者单位：河北省邯郸市第一中学)

其次:分列计算,当n=1,2,3,4,5,6,7,8,9,10时,n2的个位数只能为0,1,4,5,6,9.

猜想:对任意n∈N*,n2的个位数只能为0,1,4,5,6,9．