一首高正确率问题的课堂探究



一首高正确率问题的课堂探究

◇云南邓成美

数学学科是逻辑思维严谨的学科,对有果,错有因．数学教学探究的过程就是弄清因果的过程．有时我们看到的只是问题的表面现象,如客观选择或填空题,只要求给出正确答案即可,正确答案的得出有时只是偶然,因此需要进一步的追问探究,才能发现隐藏在假象背后的本质，进而才能切实提高学生分析问题、解决问题的能力．本文以一道期末试题的课堂探究为例,以期抛砖引玉．

题目设P、Q为一个正方体表面上的2点,已知此正方体绕着直线PQ旋转θ(0<θ<2π)角后能与自身重合,那么符合条件的直线PQ有______条.

本题是笔者所在学校一道高三期末考试试题,笔者所教授的2个班近80人,正确率超过70%．在试卷讲评时本打算一带而过．但不经意的一问引起了课堂探究．

1不经意的一问,暴露了真相

师:生1请说一下这13条直线都是哪些直线?

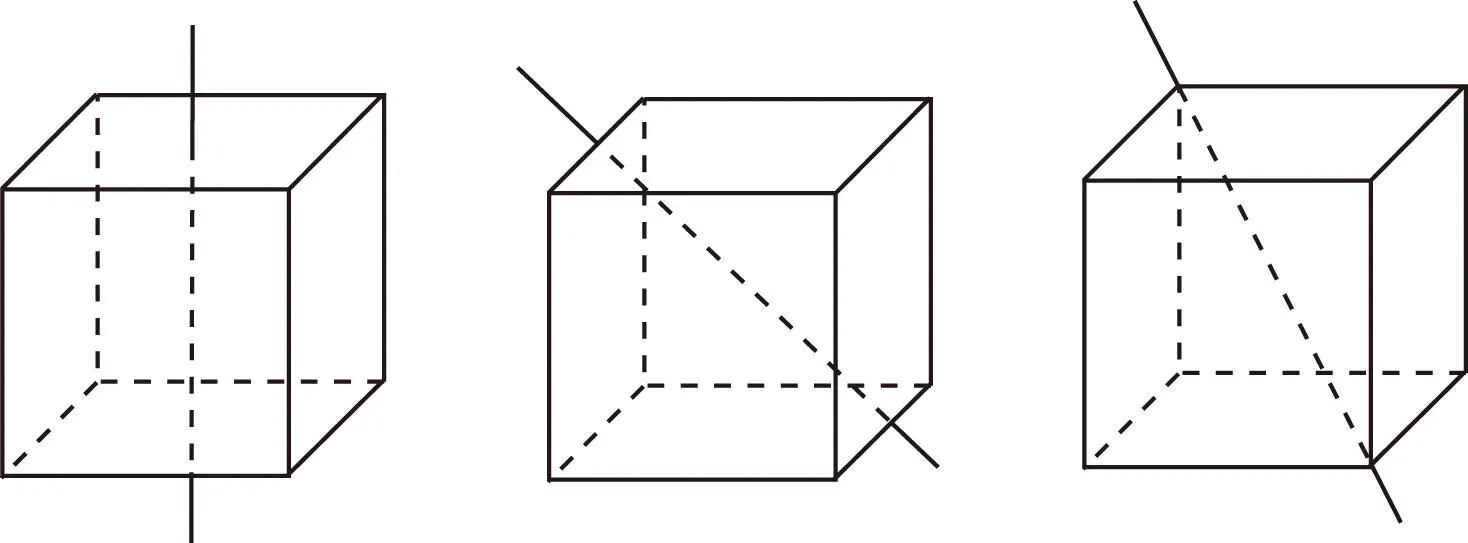
图1　　　　　　图2　　　　　　图3

生1:第1类如图1,过对面中心的直线,有3条;第2类如图2过对角棱中点的直线,有6条;第3类如图3,与体对角线重合的直线,有4条．共13条．

师:完全正确．

此时正想进入下一题目的讲评,突发奇想,又补充了1问．

师:这3种情况各自旋转了多少度后与原图像重合?

生1:第1类旋转π/2;第2类旋转π;第3类旋转π．

师:(略显诧异)大家同意生1的解答吗?

生众:(几乎异口同声)同意．

2问题初探,揭露错误本质

师:我们以第3种情况为例,如图4,在四边形AA1C1C中,点A1旋转π后与哪点重合?

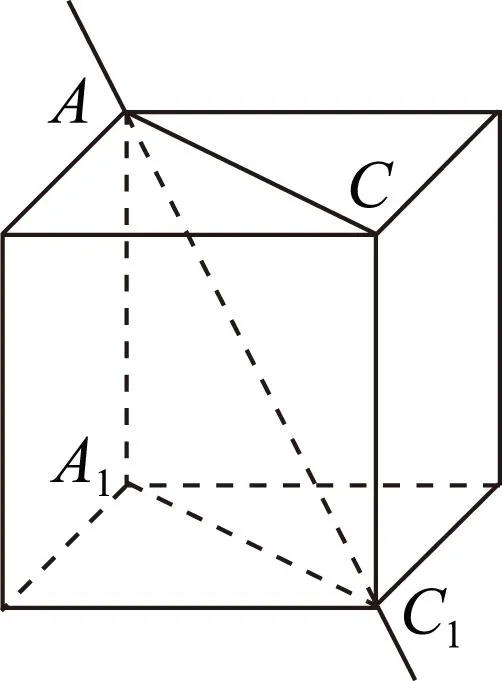
图4

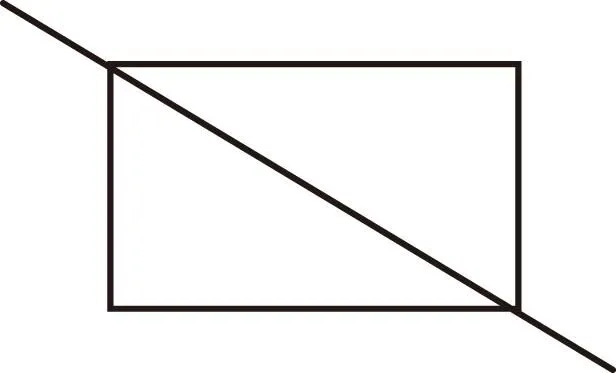
图5

生2:与点C重合．

师:四边形AA1C1C是什么图形?

生众:矩形．

师:如图5,一个矩形绕对角线旋转π后,是否与原图重合?

生众:沉默……

师:那么绕正方体对角线应该旋转多少度,能与原图重合?

此题虽然结果正确,但学生并没有真正认识到问题的本质,如果将题目改为:

变式设P、Q为一个正方体表面上的2点,已知此正方体绕着直线PQ旋转θ(0<θ<2π)角后能与自身重合,若以正方的对角线为旋转轴,则至少要旋转的角度为________.

答题结果可想而知．

3深入探究，得出解题通法

师:空间问题平面化是处理立体几何问题的有效途径,我们可以从最简单的情况入手．如第1类情况,图1的俯视图(如图6)，根据正方形的属性易知旋转π/2后与原图形重合．

运用此法请同学们分析一下另外2种情况．

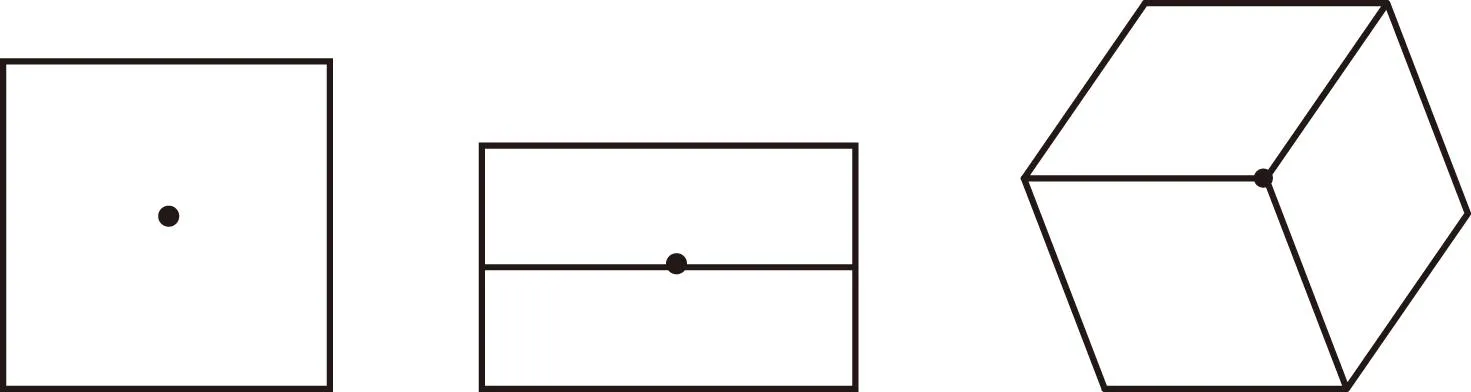
图6　　　　　图7　　　　　图8

生3:第2类情况,可令旋转轴垂直于水平面,则其俯视图如图7所示,易知旋转π后与原图形重合．

生4:第3类情况,令旋转轴垂直于水平面,则其俯视图如图8所示,易知旋转2π/3后与原图形重合．

师:如果没有强调最小的旋转角度呢?

生5:第1类情况可以旋转π/2,π,3π/2．第3类情况可以旋转2π/3,4π/3．

至此问题得到完美解决．

在平时的解题训练中我们不应满足于答案的得出,应对问题的本质进行深入探究以及对题目进行变式拓展,进而锻炼我们分析问题、解决问题的能力,以不变应万变．

(作者单位：云南省昆明市嵩明县第四中学)

答案： 13条.