结合光流跟踪和三焦点张量约束的双目视觉里程计

程传奇，郝向阳，张振杰，赵漫丹

（1. 信息工程大学 导航与空天目标工程学院，郑州 450001；2. 北斗导航应用技术河南省协同创新中心，郑州 450001）

结合光流跟踪和三焦点张量约束的双目视觉里程计

程传奇1,2，郝向阳1,2，张振杰1,2，赵漫丹1,2

（1. 信息工程大学 导航与空天目标工程学院，郑州 450001；2. 北斗导航应用技术河南省协同创新中心，郑州 450001）

针对城市街道准确实时定位的问题，提出将光流跟踪与三焦点张量约束结合的双目视觉里程计方法。为提高运算效率，将图像序列分为关键帧与非关键帧，对关键帧进行常规的特征点检测与匹配，对非关键帧用Lucas-Kanade光流跟踪特征点对。推导了基于前后帧、左右视图三焦点张量约束的观测方程，顾及动力学方程，组成卡尔曼滤波模型。考虑到观测方程的非线性，采用迭代Sigma点卡尔曼滤波进行解算，解算过程中用 RANSAC稳健估计策略提纯匹配，以增强系统整体稳健性。实验结果表明：提出的算法在基本不损失精度（X方向优于5 m，Y方向优于4 m）的情况下，计算速度提升6.2倍，单帧图像平均处理时间由0.3115 s下降为0.0503 s，能够满足城市定位实时准确的需求。

双目视觉里程计；光流；三焦点张量；迭代Sigma点卡尔曼滤波

视觉里程计（VO）是视觉导航的一种特殊形式，由于它仅利用摄像机的输入信息来估计载体的运动状态[1]，近十几年来已广泛应用于室内/外陆地机器人[2]、水下机器人[3]及无人飞行器[4]等各类机器人自主导航定位中。

因VO导航高度自主及其低成本性，吸引了相关学者和机构的关注。VO分为单目视觉里程计和双目视觉里程计两种。在单目视觉里程计方面：Forster[5]提出了一种快速半直接单目视觉里程计（Semi-Direct Monocular Visual Odometry，SVO）算法，利用双线程分别进行运动估计和地图构建，提高了运行速度；冯国虎[6]提出了惯性传感器与单目视觉里程计的组合导航算法，克服了单纯由视觉估计相机姿态精度低造成的长距离导航误差大的问题；Bachrach[7]和 Endres[8]利用 RGB-D相机搭建了运动估计、规划和构图的系统。但单目视觉由于缺少绝对尺度，在模型求解过程中，会出现尺度因子的模糊性，需要一定的约束和假设。

对于双目视觉[9]，其固定基线便可进行视差图的精确解算，可解决单目视觉中的尺度二义性。在双目视觉里程计方面：Geiger[10]提出了一种基于立体像对实时三维重建算法，可实时估计摄像机位姿信息并恢复三维场景信息；Holzmann[11]设计了基于线特征的双目视觉里程计，用IMU辅助检测直线，实现了纹理不明显环境内的定位。但以上算法在定位时都需要恢复场景三维信息，影响了实时性。Kitt[12]等人设计了一种基于随机抽样一致性（RANSAC）提纯策略的双目视觉里程计，通过计算图像序列之间三焦点张量，无需进行三维重建即可进行运动估计，但运行效率较低，难以实现实时定位。目前，光流对图像运动的估计已经可以满足一定的精度要求[13]，因其运算速度快，基于光流法的视觉里程计也有研究[14-15]。文献[16]提出把基于光流估计的VO与基于特征匹配的VO进行融合，取得了不错的效果，但基于光流的运动估计精度较低，势必会影响最终定位结果。

本文提出一种结合光流跟踪和三焦点张量约束的双目视觉里程计算法，以文献[12]算法为基础，利用光流跟踪同名点对，基于前后帧、左右视图之间的三焦点张量约束，通过卡尔曼滤波进行运动估计，以期在保证精度的同时提高算法实时性。

1 基本原理

1.1 摄像机模型

摄像机坐标XC与图像坐标x～的投影关系可表示为：

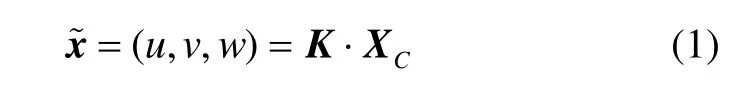
摄像机坐标系与世界坐标系之间的关系可由一个旋转矩阵R和平移向量t（外参数）来表示：

结合式(1)和(2)，可得三维点到图像坐标系的投影关系：

式中，矩阵P称为摄像机投影矩阵。

1.2 三视图几何关系

计算机视觉中，使用三焦点张量T(3×3×3)描述三视图几何关系，它仅依赖于视图间的运动和摄像机内参数，且可由这些视图的摄像机矩阵唯一确定，而与景物结构无关[17]。

已知三台摄像机的投影矩阵分别表示为：

那么三焦点张量元素可由式(4)计算：

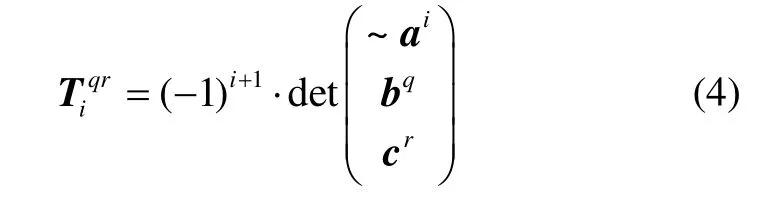
式中：～ai表示PA去掉第i行；bq表示PB的第q行；cr表示PC的第r行。

图1 三视图对应点的关系Fig.1 Relationship between corresponding points in three images

这里我们利用三焦点张量把图像A、B中的对应特征点xA↔xB映射到第三幅图像C中，如图1所示：把图像中通过点xB的任意一条直线lB投影到三维空间中。给定lB和三焦点张量T，那么有：

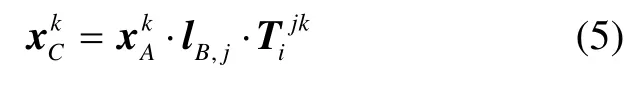
1.3 光流跟踪

光流场反映图像灰度模式的表面运动，据此可对序列图像的特征点进行跟踪。光流跟踪的一个基本假设是：序列图像的采样时间间隔很小，邻帧图像同名点的灰度值保持不变。设t时刻的光流图像为f(x,y,t)，则经过时间间隔Δt，图像点坐标(x,y)运动至(x+Δx,y+Δy)处。根据以上假设，有：

把式(6)进行泰勒展开，得到：

式(6)(7)联立，可得：

式(8)两边同时除以Δt，并使Δt→0求极限，得：

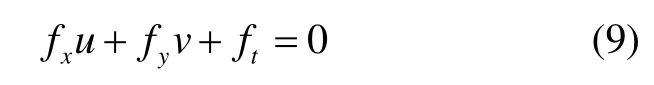
2 问题描述

视觉里程计问题就是如何由车载摄像机拍摄的连续影像，通过计算机视觉的方法，实时解算车辆的空间位置。由于摄像机固连在车辆上，所以视觉里程计实质就是对车载摄像机的实时位姿估计。

双目视觉里程计就是通过相邻时刻的双目立体像对估计摄像机运动参数。图2表示相邻时刻双目摄像机结构的示意图，它描述了像平面、摄像机坐标系以及摄像机相对于前一时刻右摄像机的位姿关系。通过事先标定，容易获取前一时刻左摄像机的相对位姿通过外参数标定和运动估计可分别获取运动参数这就是双目视觉里程计要研究的本质问题。

图2 相邻时刻双目摄像机结构的示意图Fig.2 Configuration of stereo cameras at adjacent times

3 算法实现

3.1 运动状态参数化

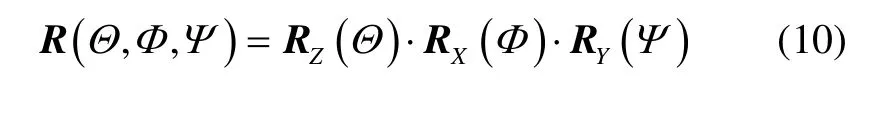
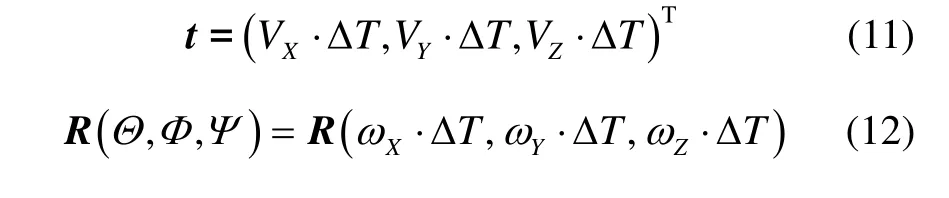
式中，Vi和ωi(i=X,Y,Z)分别表示运动速度和角速度，ΔT表示邻帧间隔时间。

3.2 三焦点张量约束的观测模型

图2中描述了摄像机投影矩阵P，不失一般性，令前一时刻右摄像机的坐标系与世界坐标系对准，即令PR,k=KR·[I|0]，那么已知旋转矩阵和平移向量后，投影矩阵由式(13)～(15)计算：

利用投影矩阵P，可计算出两个三焦点张量：TR表征当前时刻右像与前一时刻像对的关系；TL表征当前时刻左像与前一时刻像对的关系。考虑式(4)，可得：

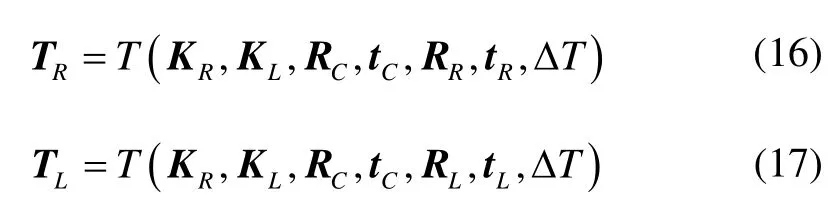
式中，TR和TL由相机内参数以及双目相机的运动参数决定。把式(16)和(17)代入三焦点张量点转移关系，即公式(5)，得到：

式中，x表示对应像点，H表示非线性函数。这就是双目视觉里程计的观测方程。

3.3 卡尔曼滤波最优估计

为更好地利用载体运动的动力学模型，采用卡尔曼滤波进行最优估计。状态参数为待估计的运动参数y=(VX,VY,VZ,ωX,ωY,ωZ)，观测方程由式(18)和(19)组成，故卡尔曼滤波模型可写为：

式中： f(·)为非线性状态转移函数；h(·)表示式(18)和(19)组成的非线性量测函数；z=(u,…,v)T表示4N维的观测向量；

k+1R,k+1,1L,k+1,N wk～N(0,Qk)表示系统误差，Qk为6×6维的系统误差协方差矩阵；vk+1～N(0,Rk+1)为观测噪声，Rk+1为4N×4N维的测量误差协方差矩阵，N为滤波使用的特征点对数。

求解上述模型，需要进行线性化。由于摄像机采样频率较高，一般情况下，认为相邻时刻载体保持匀速运动，故状态方程可写为yk+1=yk+wk。量测方程一般采用泰勒公式进行线性化，这种方式称为扩展卡尔曼滤波（Extended Kalman Filter，EKF）。EKF采用一阶泰勒展开，模型强非线性时效果不好。为减小逼近误差，状态更新阶段采用迭代方式进行，称为迭代扩展卡尔曼滤波[18]（Iterated Extended Kalman Filter，IEKF）。还有一种方式用基于构造Sigma点的UT变换进行逼近，称为无迹卡尔曼滤波（Unscented Kalman Filter，UKF），也有其迭代方式，称为迭代 Sigma点卡尔曼滤波[19-20]（Iterated Sigma Point Kalman Filter，ISPKF）。考虑精度与实时性，本文采用ISPKF进行状态估计，具体实施方案可参阅文献[19]。

3.4 特征的提取与匹配

在特征点的提取与匹配阶段，把序列影像分为两类：关键帧和非关键帧。关键帧的特征提取与匹配采用FAST算子和归一化互相关算法实现；非关键帧的特征匹配则使用 1.3节的光流跟踪算法，文中采用Lucas-Kanade光流算法进行求解。视觉里程计中最耗时的一个步骤就是特征匹配，而光流跟踪可解决该问题。

3.5 RANSAC特征提纯策略

无论是关键帧的特征提取与匹配还是光流跟踪的同名点，都不可避免存在误匹配点，若不加判断的采用所有匹配点进行滤波运算，会影响解算结果，严重时会引起发散。这里采用采用随机抽样一致（RANSAC）算法设计稳健估计策略。具体实现步骤如下：

1）从同名点对中随机选取S个点对作为抽样子集，因运动估计算法中至少需要3个点，故S≥3；

2）基于该子集，利用3.3节的ISPKF估计运动参数；

3）基于运动参数计算所有同名点对的重投影误差（这里采用欧氏距离），若误差大于设定阈值，认为该点为外点，反之，为内点；

4）利用所有内点基于ISPKF重新估计运动参数。

3.6 算法实现流程

本文设计的视觉里程计流程如图3所示，具体包括以下步骤：

Step1：车辆运动中实时采集图像序列。当前图像为关键帧时，进行特征点提取与匹配；当前图像为非关键帧时，进行特征点光流跟踪，进而按照 Lucas-Kanade光流算法进行同名点定位。

Step2：获取同名点后，即可得到系统观测模型，即式(21)。

Step3：联合系统状态模型，利用ISPKF进行解算，获取状态最优估计。若当前图像为关键帧，则直接进行位姿更新；若当前图像为非关键帧（图3中粗实线部分），则利用当前获取位姿进行内点率判定，若通过，则更新位姿，若不通过，则把当前图像当作关键帧重新进行运算。

若未能获取足够多的内点，则无法构建量测方程，此时直接进行状态预报更新位姿，保证系统整体的稳健性。

图3 视觉里程计设计原理图Fig.3 Flow chart of visual odometry

4 实验与分析

4.1 实验数据介绍

搭建实验平台（搭载Flea2 Firewire相机和OXTS RT 3000 IMU/GPS组合测量系统的车辆），在城市中进行跑车实验。采集的数据包括Flea2 Firewire相机采集的高质量立体图像序列，以及 OXTS RT 3000 IMU/GPS测量系统采集的地理数据（把它作为真值）。预先在标定场进行相机标定。文中实验数据集具体参数见表1。

如图4所示，图4(a)(b)(c)为连续三帧影像（篇幅所限，这里只显示了左相机采集影像），图4(c)中黑色线条为光流跟踪的特征点效果。光流场正确地反映了运动场，图中黑色线条方向主要为径向，说明车辆在前行。

表1 实验数据集参数Tab.1 Parameters of datasets

图4 图像序列以及光流跟踪效果显示Fig.4 Image sequences and effect of optical-flow tracking

4.2 算法性能分析

为验证本文算法的有效性，把本文算法与 Bernd Kitt等提出的视觉里程计算法（以下简称Kitt算法）进行对比分析，具体解算结果如图(5)～(8)所示。本文中所有实验都在MATLAB 2012B中进行，实验环境为Lenovo E530笔记本电脑（酷睿i5-3210CPU，主频2.50 GHz，4G内存）。

图5为本文算法、Kitt算法解算轨迹与IMU/GPS测量轨迹对比图。相机中心与IMU/GPS中心不重合，相对于 IMU/GPS，相机在天向、前向、左侧分别有1.8 m、0.58 m、0.12 m 的偏移。另外，相机相对于IMU/GPS的俯仰角为-3.7°。这里进行对比时，已经把两种数据对准，可以看出，两种算法解算的轨迹都与真值吻合，验证了算法的合理性。

图5（a） 解算轨迹（数据集1）Fig.5(a) Results of the proposed method and Kitt’s method (Dataset 1)

图5（b） 解算轨迹（数据集2）Fig.5(b) Results of the proposed method and Kitt’s method (Dataset 2)

图6为两种算法解算X、Y方向误差，可以看出，两种算法在两个方向上误差都是越来越大，但整体误差在可接受范围之内。这是由于视觉里程计每次解算出相机在采集邻帧图像时刻的相对位姿，然后根据相对位姿进行航迹推算，这种导航方式不可避免会产生误差累积效应。另外，数据是在城市中采集的，不可避免地有遮挡等因素引起GPS失效，故OXTS RT 3000 IMU/GPS测量系统的精度并没有达到标称精度（优于0.05 m）。这里把它作为真值，主要是比较两种算法的相对优劣。

图 7为本文算法与 Kitt算法解算结果的相对误差。容易看出，本文算法精度与Kitt算法相当，数据集1和数据集2的解算结果X方向误差在5 m以内，Y方向误差在4 m以内。

综上所述，实验结果可以验证本文算法运动估计的可靠性与正确性。

图6（a） 解算误差（与IMU/GPS数据对比）（数据集1）Fig.6(a) Errors of the proposed method and Kitt’s method with respect to IMU/GPS (Dataset 1)

图7（a） 本文算法误差（与Kitt算法相比）（数据集1）Fig.7(a) Errors of the proposed method with respect to Kitt’s method (Dataset 1)

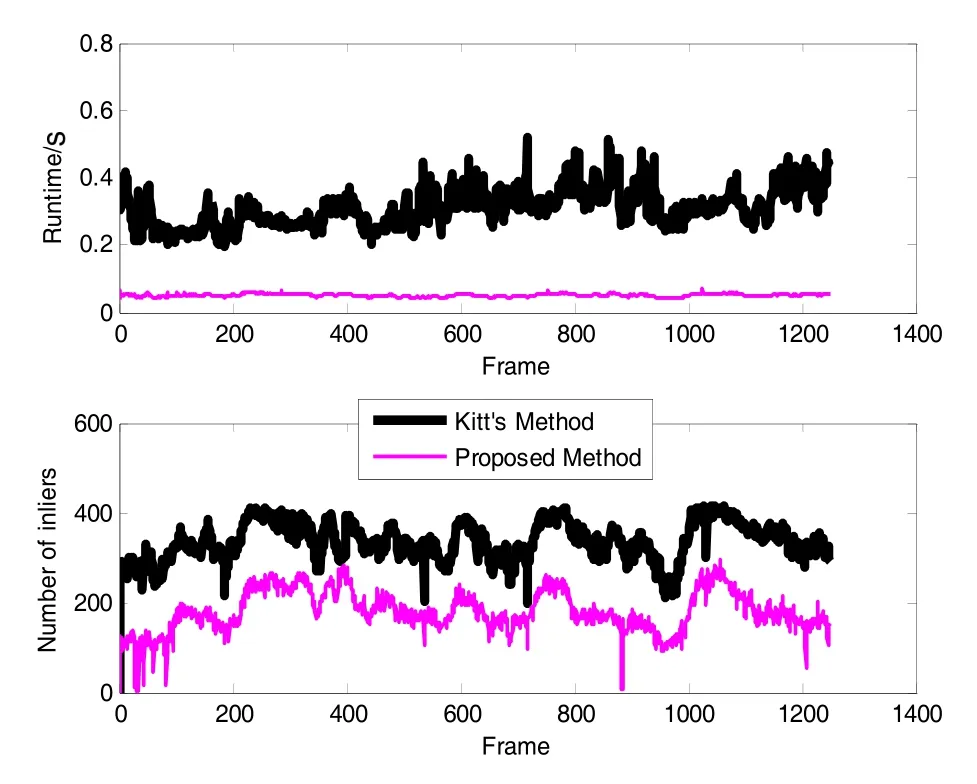
图8（a） 算法运行时间与匹配内点数目（数据集1）Fig.8(a) Runtime and number of inliers of the proposed method and Kitt’s method (Dataset 1)

图6（b） 解算误差（与IMU/GPS数据对比）（数据集2）Fig.6(b) Errors of the proposed method and Kitt’s method with respect to IMU/GPS (Dataset 2)

图7（b） 本文算法误差（与Kitt算法相比）（数据集2）Fig.7(b) Errors of the proposed method with respect to Kitt’s method (Dataset 2)

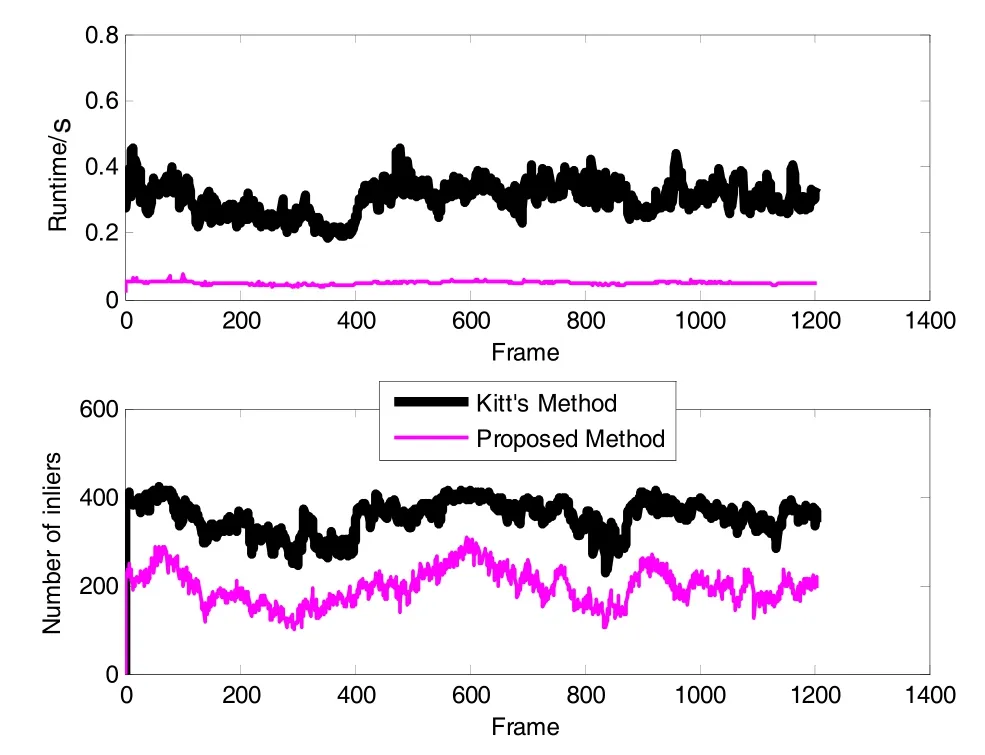
图8（b） 算法运行时间与匹配内点数目（数据集2）Fig.8(b) Runtime and number of inliers of the proposed method and Kitt’s method (Dataset 2)

图8为算法运算时间与匹配内点数对比。容易看出，虽然本文算法匹配内点数有所减少（平均内点数由296减少为122），但经过上述分析，解算精度并未损失多少（X方向优于5 m，Y方向优于4 m）；同时可看出，本文算法运行效率显著提升，Kitt算法单帧影像平均处理时间为0.3115 s，本文算法单帧影像平均处理时间为0.0503 s，速度提升了6.2倍，且在消费级笔记本电脑配置下实现了实时导航定位，充分说明了算法在实时性方面的优越性，能够满足车辆在城市街道实时准确定位的需求。

5 结 语

本文提出了一种结合光流跟踪和三焦点张量约束的双目视觉里程计算法以提高车辆城市导航的精度和实时性，推导了基于三焦点张量约束的图像序列观测方程，结合载体动力学模型，建立了双目视觉里程计的 ISPKF运动参数估计方法。在运动估计过程中用光流跟踪策略定位图像同名点，并以 RANSAC稳健估计策略提纯同名点，城市实测实验数据验证了算法的优良性能。但视觉里程计航迹推算导航的本质使得定位误差会累积，因此与其他传感器的组合导航就显得尤为重要，下一步将开展组合模式的视觉里程计算法研究。

（References）：

[1] Yousif K, Bab-Hadiashar A, Hoseinnezhad R. An overview to visual odometry and visual SLAM: Applications to mobile robotics[J]. Intelligent Industrial Systems, 2015, 1(4): 1-23.

[2] Konolige K, Agrawal M, Solà J. Large-scale visual odometry for rough terrain[J]. International Journal of Robotics Research, 2011, 66: 201-212.

[3] Wongsuwan K, Sukvichai K. Visual odometry estimation for an underwater robot navigation[C]//International Technical Conference on Circuits Systems, Computers and Communications. 2015: 496-499.

[4] Annaiyan A, Yadav M, Olivares-Mendez M A, et al. Visual odometry based absolute target geo-location from micro aerial vehicle[C]//IEEE International Conference on Robotics, Automation, Control and Embedded Systems. 2015: 1-7.

[5] Forster C, Pizzoli M, Scaramuzza D. SVO: Fast semidirect monocular visual odometry[C]//IEEE International Conference on Robotics & Automation. 2014: 15-22.

[6] 冯国虎, 吴文启, 曹聚亮, 等. 单目视觉里程计/惯性组合导航算法[J]. 中国惯性技术学报, 2011, 19(3): 302-306. Feng Guo-hu, Wu Wen-qi, Cao Ju-liang, et al. Algorithm for monocular visual Odometry/SINS integrated navigation[J]. Journal of Chinese Inertial Technology, 2011, 19(3): 302-306.

[7] Bachrach A, Prentice S, He R, et al. Estimation, planning, and mapping for autonomous flight using an RGB-D camera in GPS-denied environments[J]. International Journal of Robotics Research, 2012, 31(11): 1320-1343.

[8] Endres F, Hess J, Sturm J, et al. 3-D mapping with an RGB-D camera[J]. IEEE Transactions on Robotics, 2014, 30(1): 177-187.

[9] 李宇波, 朱效洲, 卢惠民, 等. 视觉里程计技术综述[J].计算机应用研究, 2012, 29(8): 2801-2805. Li Yu-bo, Zhu Xiao-zhou, Lu Hui-min, et al. Review on visual odometry technology[J]. Application Reasearch of Computers, 2012, 29(8): 2801-2805.

[10] Geiger A, Ziegler J, Stiller C. StereoScan: Dense 3d reconstruction in real-time[J]. IEEE Intelligent Vehicles Symposium, 2011, 32(14): 963-968.

[11] Holzmann T, Fraundorfer F, Bischof H. Direct stereo visual odometry based on lines[C]//International Conference on Computer Vision Theory and Applications. 2016.

[12] Kitt B, Geiger A, Lategahn H. Visual odometry based on stereo image sequences with RANSAC-based outlier rejection scheme[C]//IEEE Intelligent Vehicles Symposium. 2010: 486-492.

[13] Sun D, Roth S, Black M J. Secrets of optical flow estimation and their principles[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition. 2010: 2432-2439.

[14] Campbell J, Sukthankar R, Nourbakhsh I. Visual odometry using commodity optical flow[J]. Proceedings of the American Association of Artificial Intelligence (AAAI), 2004: 1008-1009.

[15] Wang C, Zhao C, Yang J. Monocular odometry in country roads based on phase-derived optical flow and 4-DOF ego-motion model[J]. Industrial Robot, 2011, 38(5): 509-520.

[16] 郑驰, 项志宇, 刘济林. 融合光流与特征点匹配的单目视觉里程计[J]. 浙江大学学报(工学版), 2014, 42(2): 279-284. Zheng Chi, Xiang Zhi-yu, Liu Ji-lin. Monocular vision odometry based on the fusion of optical flow and feature points matching[J]. Journal of Zhejiang University (Engineering Science), 2014, 42(2): 279-284.

[17] Hartley R, Zisserman A. Multiple view geometry in computer vision[M]. 2nd ed. Cambridge University Press, 2008.

[18] Shojaei K, Shahri A M. Experimental study of iterated Kalman filters for simultaneous localization and mapping of autonomous mobile robots[J]. Journal of Intelligent & Robotic Systems, 2011, 63(3-4): 575-594.

[19] Sibley G, Sukhatme G, Matthies L. The iterated sigma point Kalman filter with applications to long range stereo [C]//Conference: Robotics: Science and Systems, 2006.

[20] Huang Y, Zhang Y, Li N, et al. Design of sigma-point Kalman filter with recursive updated measurement[J]. Circuits Systems & Signal Processing, 2015: 1-16.

Stereo visual odometry based on Kalman fusion of optical flow tracking and trifocal tensor constraint

CHENG Chuan-qi1,2, HAO Xiang-yang1,2, ZHANG Zhen-jie1,2, ZHAO Man-dan1,2
(1. School of Navigation and Aerospace Engineering, Information Engineering University, Zhengzhou 450001, China; 2. Beidou Navigation Technology Collaborative Innovation Center of Henan, Zhengzhou 450001, China)

For the problem of real-time precise localization in the urban street, a stereo visual odometry based on Kalman fusion of optical-flow tracking and trifocal tensor constraint is proposed. To speed up the algorithm, the image sequences are classified into key frames and non-key frames. A conventional featurepoint detection and matching method is utilized to process the key frames, and the Lucas Kanade optical flow method is utilized to track the correspondences in non-key frames. The mathematical model of observation based on trifocal tensor constraint among image triples is derived, which is combined with dynamic equation to form the Kalman filter model. An iterated sigma-point Kalman filter is employed to cope with the nonlinear system. To improve the robustness of the visual odometry, a RANSAC-based method is applied into the pure matching points in motion estimation. Experimental results demonstrate that, compared with Kitt’s method, the proposed method can acquire the same accuracy with the speed increasing 6.2 times, i.e., the error in the X direction and Y direction is 5 m and 4 m, respectively, while the average runtime of single frame decreases from 0.3115 s to 0.0503 s, which meets the needs of real-time accurate localization in cities.

stereo visual odometry; optical flow; trifocal tensor; iterated sigma-point Kalman filter

V448.2

：A

2016-04-18；

：2016-07-08

国家863计划资助项目（2015AA7034057A）；国家自然科学基金项目（61173077）

程传奇（1989—），男，博士生，主要研究导航定位与位置服务。E-mail: legend3q@163.com

1005-6734(2016)04-0473-07

10.13695/j.cnki.12-1222/o3.2016.04.010