一种改进的基于全局最小能量泛函光流算法
2014-11-22张起贵
张起贵,张 妮
(太原理工大学 信息工程学院,山西 太原 030024)
在三维空间物体到二维成像平面上,光流即为空间运动目标像素在其成像平面的瞬时速度,主要用于图像分割与运动目标的检测,目前已被广泛应用于医学、军事以及智能等领域.针对Horn-Schunck 提出的光流计算变分方法,J.Colliez[1]采用了基于向量的回归方法计算平滑的光流矢量,但不适合在大位移下进行光流的检测.目前,光流的主要研究方法是采用J.Colliez提出的由粗到精的分层细化技术[2],即基于最小二乘法矩阵,在图像较为平坦的区域,灰度梯度为零;在其他一些区域,二次矩阵的特征值可能接近为0.这样图像的孔径问题仍然存在,而且不能提供一个可靠完整的密度流,同时采用高斯分布[3]预处理图像,无法自适应选择平滑阈值,平滑过大,会丢失图像的较多细节信息;平滑过小,又无法有效地去除噪音,导致计算光流存在误差.因此,本文采用一种多尺度多分辨率的全局能量泛函光流计算方法,为防止过平滑而导致目标边缘细节丢失,采用基于ROF模型预处理得到的纹理图像,作为多分辨率、大尺度的输入图像,并对因环境光照影响,目标遮挡、自旋转造成的异常光流矢量值进行及时修正.
1 整体算法设计

图1 算法设计流程Fig.1 Process of algorithm design
本文整体算法思路包括:全变分正则化预处理图像,保留图像的细节信息,双线性插值分层细化图像作为金字塔各层处理图像[4],利用有限的迭代Horn-Schunck(HS)光流算法计算各层的光流矢量,利用自适应邻域修正法对异常光流矢量进行修正,并用双三次插值初始化下一层光流矢量.其具体算法流程如图1 所示.先用ROF模型[5]得到图像的纹理结构作为金字塔的预处理图像,采用高斯滤波和亚像素图像多分辨率分层细化的变形分层技术处理不同尺寸、不同分辨率的金字塔图像.设k为金字塔层数,第k层金字塔图像长、宽分别为第k-1层图像长、宽的1/2,从最低分辨率和最小尺寸图像层开始计算,第k层初始光流.定义第k-1层初始光流为双三次插值下采样第k层光流矢量的2倍,其中uk,vk为第k层经有限迭代后达到的稳态解.在图像分层过程中,缩小了光流的位移量,因此只需通过有限的迭代来计算每层的光流矢量,直至达到稳态解,将最终计算得到的光流利用彩色显示方案进行输出.
2 ROF 模型
因全局过平滑导致目标形状细节信息严重丢失,因此图像在梯度变化较大、物体边缘的地方出现了模糊现象,导致光流估计值精度降低.为此采用基于前向差分的ROF模型[6]对输入图像进行预处理时,使图像在梯度变化较小的地方得到较多的平滑,相反较少的平滑应用在图像梯度变化多的地方,其模型如下:
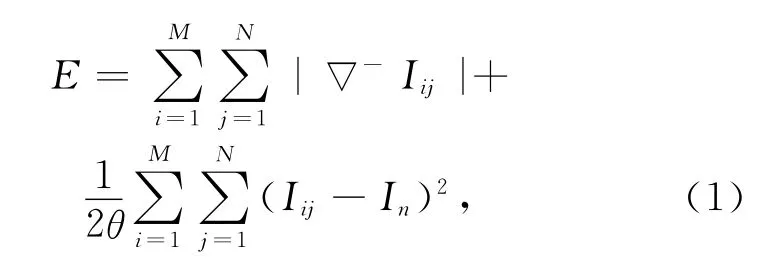
式中:In为含噪输入图像;Iij为输出图像,通过最小换能量泛函数来求解.为防止梯度变化为0,此时引入一个辅助对偶变量ξij,可得
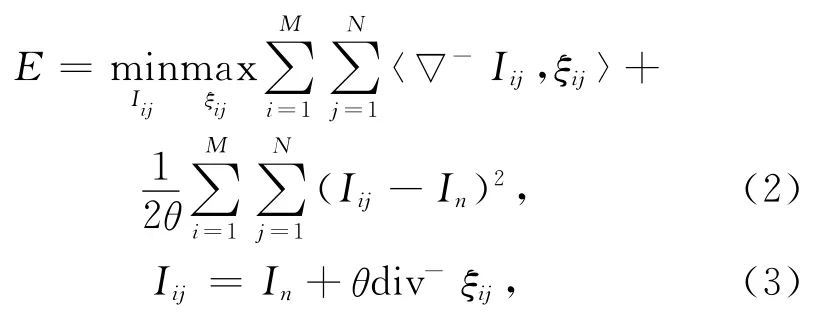
其中变量ξij可通过式(4)和(5)求得
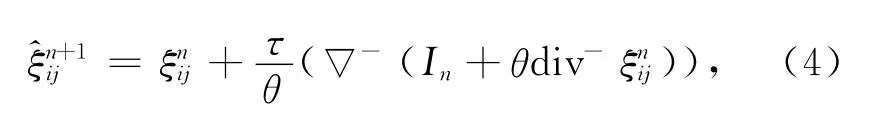
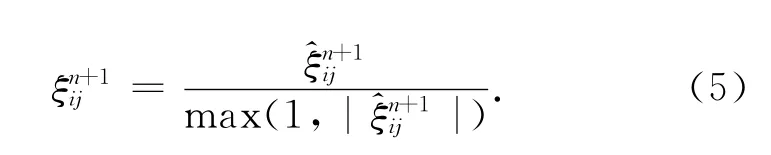
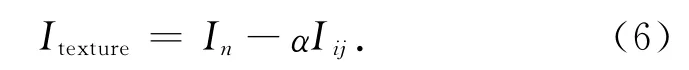
图2 为图像预处理连续输入两帧图像的过程,左列为原始图像,经ROF 模型处理后得到中间列大尺度图像,其右列所示图像中细小变化部分即纹理部分.

图2 图像预处理Fig.2 Image preprocessing
3 基于全局能量泛函的光流
基于本文研究的内容及对象,采用由粗到精的分层HS(全局)能量泛函光流模型[7-8],如式(7)所示.
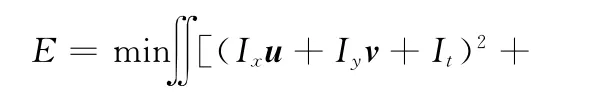

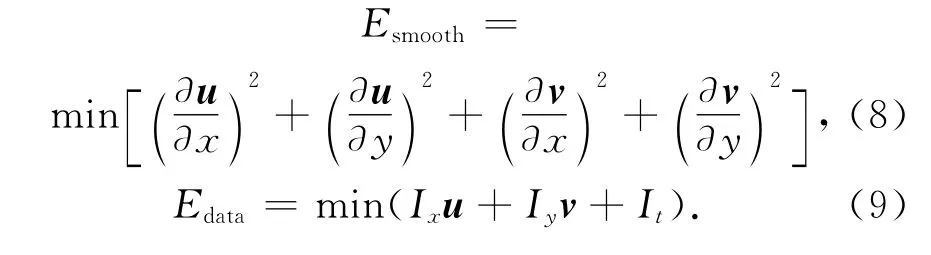
由HS光流能量泛函整理可得
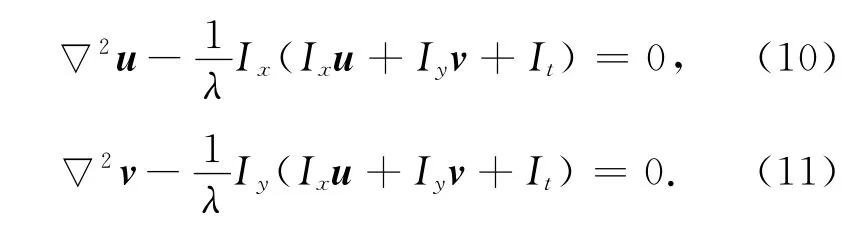
由式(10)和(11)转化为稀疏线性方程,当给定一个初始值后,经时间辅助变量即有限迭代,基本可使光流矢量(u,v)达到稳态解.设x:=(x,y,t)T,w:=(u,v,1)T,且在每次迭代过程后更新多分辩率图像I的偏微分
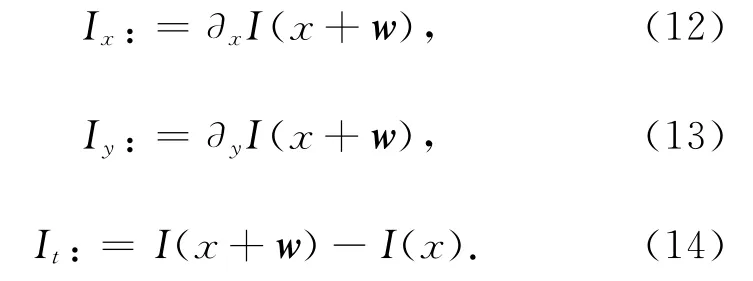
4 自适应邻域修正
对由目标的遮挡、自旋转造成的光流估计值产生的异常值,本文采用一种自适应邻域修正法,对异常光流矢量进行修正.设图像坐标为(i,j)处的光流矢量为(ui,j,vi,j),采用3×3邻域模板(如图3 所示),判断(ui,j,vi,j)是否异常.
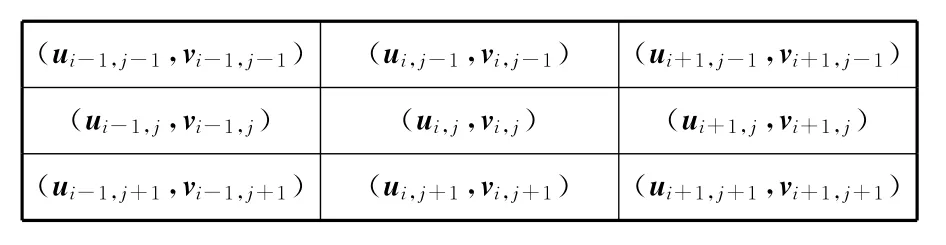
图3 3*3邻域模板Fig.3 3*3neighborhood template
1)设(ui,j,vi,j)在3×3邻域模板的光流估计平均值为,标准方差为σ(ui,j),σ(vi,j),其计算公式如下:
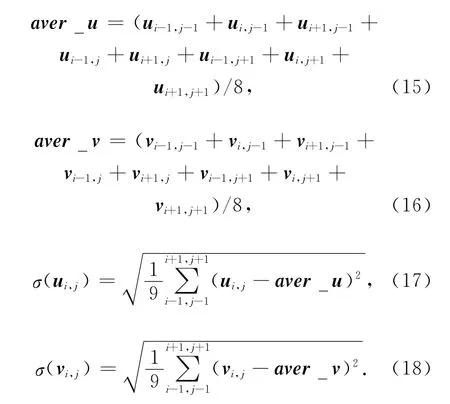
3)当ui,j异常时,采用5×5 邻域光流中值median(ui,j)修正ui,j;当vi,j异常时,采用5×5邻域光流中值median(vi,j)修正vi,j;继续步骤5).
4)采用3×3邻域光流中值median(ui,j)修正ui,j,median(vi,j)修正vi,j;继续步骤5).
5)i=i+1,j=j+1,返回步骤1),直至i=M,j=N(M×N为图像的大小).
5 彩色光流显示及算法评价
5.1 彩色光流显示
光流彩色显示较传统有向线段表示方式包含了更多的信息,运用彩色显示不仅可直观地了解运动目标的运动方向和运动幅度的大小,且更易于捕捉到细节信息.本文采用的光流显示方案是基于HSI模型,RGB 模型,设I(亮度)固定,将红、绿、蓝、紫色调间的连续变化用一个色彩盘表示,如图4 所示.
设HSI模型中色调H,饱和度S分别为
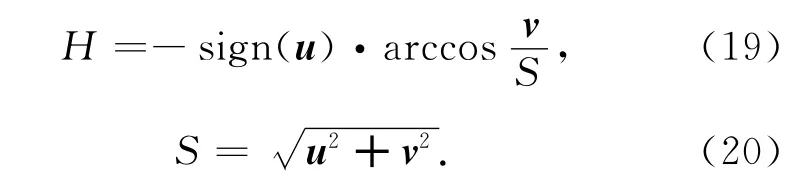
将HSI模型转换成RGB模型后,光流场则可通过光流彩色坐标系直接显示出来,图2所示的连续视频帧中,图像大小为640×480,计算光流结果显示如图5 所示.图5(a),(d)为传统光流显示图,虽然能够显示计算得到的光流结果,但不具有直观性;图5(b),(e)为光流彩色显示图,通过图5(c)头部光流的局部放大,可以看出头部光流方向是右斜向下的,满足连续视频帧运动情况.同理,图5(f)为小狗腿部光流的局部放大,小狗腿部光流方向是向左的,同样满足连续视频帧运动情况.

图4 光流彩色坐标系Fig.4 Coordinate system of color optical flow

图5 光流矢量显示Fig.5 Display of optical flow vector
5.2 算法评价
光流算法的评价直接关系到光流的计算质量及算法的优良程度,也是检验在复杂场景下运动目标的有效性[9-10].本文采用第二代Middebury光流测试库的非刚体、大位移等情况下的真实光流场进行测试,对于误差主要发生在运动边缘、灰度梯度变化小及大尺度图像运动的区域,采用平均角误差、平均终点误差、光流矢量角度标准差进行光流精度的对比.
平均角误差是衡量整个光流场角误差的平均值,是指测试光流(ui,j,vi,j,t)与真实光流(uith,ith,vith,jth,t)之间的夹角,经过反余弦运算获得角度误差,避免了零值光流问题的出现.用平均终点误差来衡量整个光流场矢量误差的平均值,光流矢量角度标准差是衡量整个光流场角度误差的波动性,三种算法评价如式(21)~(24).
1)平均角误差(AAE)
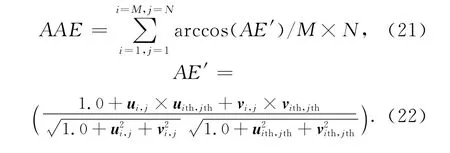
2)平均终点误差(AEPE)
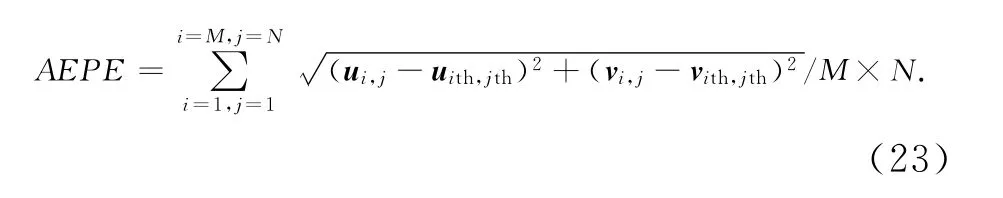
3)光流矢量角度标准方差(σ)

5.3 实验仿真
本实验是在Matlab 2008a环境下进行的数据仿真,连续选取Middebury 光流测试库的第10帧、第11帧图像作为输入视频帧,通过本文提出的改进算法,得到了如图6 所示的光流彩色显示图.定义超过10 像素位移运动为大位移运动,Grove3,Hydrange,Urban2,Urban3图像即为超过10像素的大位移运动的目标图像,并且通过表1对比光流算法.设THS代表传统HS光流算法,PHS代表金字塔HS光流算法,IHS代表改进的HS算法.通过对比,可明显观察到,对于纹理复杂、相对摄像机的大位移运动目标,光流计算AAE,AEPE,σ值有明显减小.
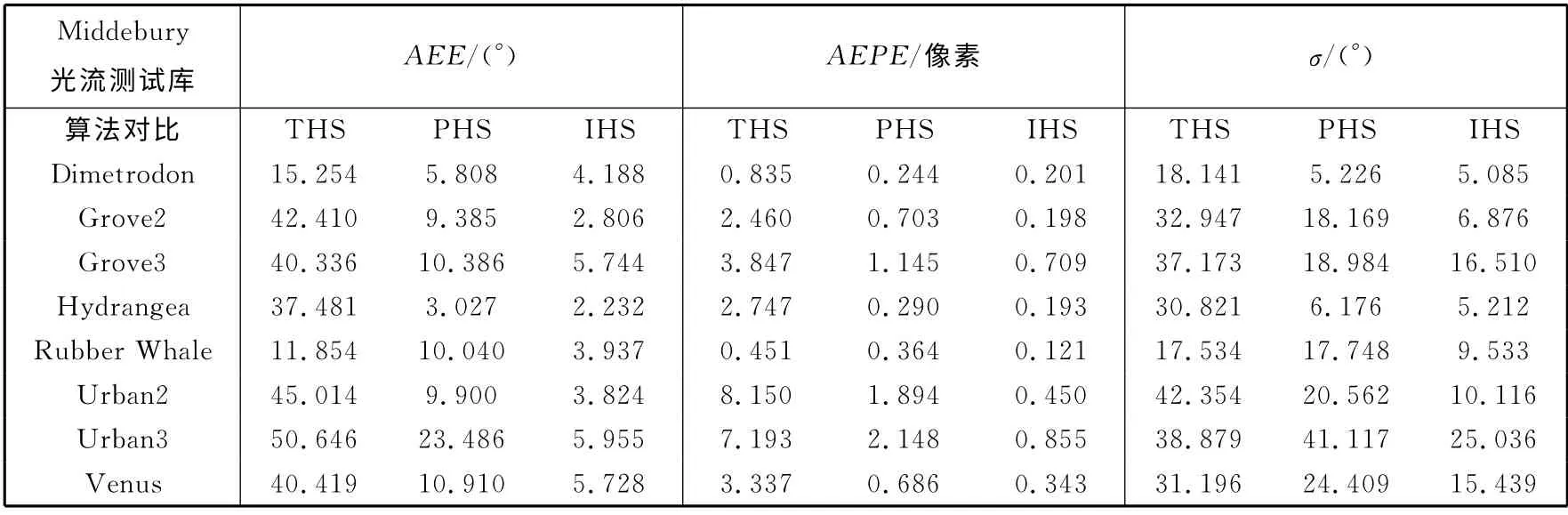
表1 HS光流实验数据Tab.1 Experimental data of HS optical flow


图6 光流彩色显示Fig.6 Display of color optical flow
6 结论
针对复杂场景下大位移、非刚性运动目标的光流矢量检测,本文提出了一种改进的基于ROF模型的全局能量泛函光流法,不仅克服了过平滑造成目标形状的失真,外界环境对光流预处理图像的影响,而且利用自适应邻域修正法修正了异常光流矢量,同时实现了小位移和大位移运动目标的光流计算.相比于传统Horn-Schunck算法与金字塔Horn-Schunck算法,AAE平均误差分别降低了87.86%,58.51%,AEPE平均误差分别降低了89.44%,58.99%,提高了算法的精确度和鲁棒性.在今后研究提高算法精度的同时,将进一步缩短时间代价,为后续光流算法的应用奠定了一定的基础.
[1]Colliez J,Dufrenois F,Hamad D.Optic flow estimation by support vector regression[J].Engineering Applications of Artificial Intelligence,2006,19(7):761-768.
[2]张金林.基于改进的Lucas-Kanade光流估算模型的运动目标检测[J].微计算机信息,2010,26(8):194-196.Zhang Jinlin.Moving object detection based on improved Lucas-Kanade optical flow model[J].Microcomputer Information,2010,26(8):194-196.(in Chinese)
[3]卫保国,李晶.一种针对大尺度运动的快速光流算法[J].计算机应用与研究,2012,29(9):3351-3357.Wei Baoguo,Li Jing.Fast optical flow algorithm for large-scale motion[J].Application Research of Computers,2012,29(9):3351-3357.(in Chinese)
[4]陈震.图像序列光流计算技术及其应用[M].北京:工业出版社,2012.
[5]王玲玉.图像去噪的非局部正则化方法研究[D].武汉:武汉理工大学,2012.
[6]Brox T,Bruhn A.High accuracy optical flow estimation based on a theory for warping[J].Proc.8th European Conference on Computer Vision,2004,3024:25-36.
[7]Papenberg N.Highly accurate optical flow computation with theoretically justified warping[J].Interna-tional Journal of Computer Vision,2006,67(2):141-158.
[8]廖彬.单目视频中光流场估计视频的研究[D].广州:华南理工大学,2011.
[9]Sun D.Learning optical flow[C].Computer Vision-ECCV 2008,Berlindelberg:Springer-verlcg,2008:83-97.
[10]Baker S,Scharstein D,Lewis J P,et al.A database and evaluation methodology for optical flow[J].International Journal Computer Vision,2011,92(1):1-31.
