基于人体多方位运动的三维自主导航定位算法

刘 宇，周 帆，李云梅，路永乐，彭 慧，张 欣

（1. 重庆邮电大学 光电信息感测与传输技术重庆市重点实验室，重庆 400065；2. 中国电子科技集团第二十六研究所，重庆 400065）

基于人体多方位运动的三维自主导航定位算法

刘 宇1，周 帆1，李云梅1，路永乐1，彭 慧2，张 欣1

（1. 重庆邮电大学 光电信息感测与传输技术重庆市重点实验室，重庆 400065；2. 中国电子科技集团第二十六研究所，重庆 400065）

基于MEMS传感器的行人导航通常利用行人航迹推算算法解算出人体位置的坐标对行人定位。传统行人航迹推算算法只能用于单一前进行走运动模式，不适用于人体实际的多方位运动模式。因此，提出了一种多方位运动三维自主导航定位算法，利用三轴加速度计数据对行人进行步态检测和步长估计，在分析了加速度计单轴数据的基础上，讨论了4类运动模式的识别方法，推导出适用于人体多方位运动模式的航迹推算公式。在智能手机平台上进行测试验证，实验结果表明，所提出的多方位运动模式自主导航定位算法在人体实际运动中，定位误差小于3.2%，很大程度上提高了导航精度。

MEMS传感器；三维自主导航；航迹推算；多方位

惯性系统不需要外部参考系、不向外部辐射能量，也不依赖于外部信息，是一种自主导航系统，可全时间地工作于空中、地球表面乃至水下。惯性系统能提供位置、速度、航向和姿态角信息，所产生的导航信息连续性好并且数据更新率高[1]。

很多提高行人导航的精度的研究，主要集中在传感器校准及算法优化的角度。Nilsson研究了基于鞋式的行人导航系统，文章中采用了两个惯性测量单元绑在脚上，虽然降低了算法复杂度，但是在硬件上产生了很大的开销[2]。Fan Li采用粒子滤波对步长和航向进行估计，但是算法中需要有本地地图对行人的行走轨迹进行限制，对于缺少室内地图的情况则不适用[3]。Schindhelm采用惯性传感器判别行人的运动模式，但只分析了前进行走运动模式[4]。李昊提出了前进行走和后退行走的方位识别，但相对人体实际的多方位运动模式仍不完善[5]。

人体实际运动包括4个方位的运动模式，前进行走、后退行走、左横向行走和右横向行走。如果不进行区分，将导致导航轨迹与实际相反或垂直，引起不可估量的误差。为了解决这个问题，本文提出一种基于人体多方位运动的三维自主导航定位算法。

1 系统介绍

智能手机的底层硬件、通信能力和计算能力完全能够满足定位与导航需求。本系统采用华为智能手机作为行人自主导航系统的硬件测试平台，该设备集成了多个传感器，如加速度传感器、磁力传感器、陀螺仪、距离传感器和气压计等。

多方位运动三维自主导航定位算法的系统架构如图1所示。首先，对三轴加速度计、三轴磁力、计三轴陀螺仪和气压计进行数据预处理；然后，通过数据融合得到行人每一步的航向，利用加速度数据检测行人的步态和步长。使用峰值检测法与相位反转法区分前进行走、后退行走、左横向行走，右横向行走4类行走运动模式，气压计用来解算高度；最后，通过本文提出的多方位运动三维定位算法得到行人的坐标进行定位。

图1 系统框架Fig.1 System architecture

2 导航算法

式(1)是传统的航迹推算算法，该算法利用航向、步长和高度计算出行人的坐标对行人定位，算法模型如图2所示[6-7]。

式中，Lk为每一步的步长，θ为每一步的航向，Vk为高度差，E(k)、N(k)、H(k)分别表示东向、北向、高度。

图2 航迹推算算法模型Fig.2 Model for PDR algorithm

2.1 步态检测

加速度计原始值输出的波形会产生多峰值现象，易造成计步误判，不利于步态的判别，因此，需要对加速度信号做预处理[8]。对于原始数据的预处理，需要消除各种噪声，并尽量多地保留原始数据的特征。通过滤波处理可以使加速度曲线更加平滑，更适合特征提取和分类[9]。本文采取的是汉明窗滤波，窗口大小为 5。滤波后加速度的数据呈规律性变化，每一个跨步对应一个峰值、一个零点和一个谷值，类似于一个正弦波。本文利用峰值检测法来检测步态，图3是加速度计滤波后的波形图，行人每一步的峰值都被标记了出来，从而验证了该步态检测算法的有效性[10]。

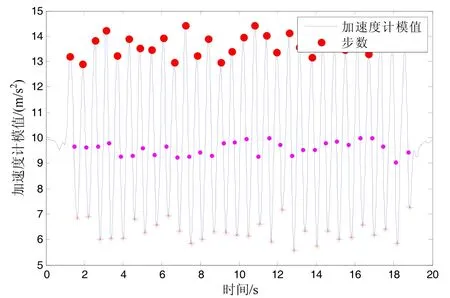
图3 步态判别Fig.3 Detection of step

2.2 步长估计

步长估计是影响定位精度的关键因素，因此步长估计成为航迹推算算法的研究重点。步长估计的算法有线性模型、人体运动模型、经验模型、神经网络模型等[11]。

本文使用一种常用且精度相对较高的线性模型来进行步长估计，影响行人步长的因素主要是步频和行人身高，因此本文使用了行人身高与步频来计算行人步长，计算公式为

式中，h为行人的身高，fstep为行人行走的步频，a、b、c为线性模型的校准系数，通过大量的训练数据可以得到校准系数a、b、c的值。

2.3 高度解算

由于外界环境的影响使得在相同楼层大气压也会有跳变，造成求出的高度不稳定。因此需要对气压值滤波，首先利用式(3) 滑动加权平均法对气压计数据处理，然后用式(4)中值滤波算法滤波，最后把气压值转换成高度。

式中：Xk为第k个均值，M为时间窗的长度，wi为权值；iP为t时刻的原始气压值，P(t)为t时刻滤波后的气压值，单位为Pa；Xmid为5个均值的中值。

气压计测量的气压值经过滤波，然后利用式(5)把气压值转换成高度，直接用于人体高度的判别。

式中：H(t)为高度，单位为m；P(t)是t时刻滤波后的气压值，单位为Pa；P(0)是起始时刻的气压值，单位为Pa。

3 多方位运动航迹推算

3.1 纵向航迹推算

传统的航迹推算算法存在的缺陷是，行人后退行走、左横向行走及右横向行走时与前进行走的航向一样，定位轨迹一直向前更新，造成导航轨迹与实际相反或垂直，引起较大的误差。

如图4所示为二维运动模型，行人从A点前进行走到B点，再从B点后退行走到C点，这个过程有两次跨步且航向不变。如果使用传统的航迹推算算法，行人的位置会在D点，这与实际运动轨迹相反，这种情况下传统的航迹推算算法不再适用。

图4 航迹推算算法模型Fig.4 Model for PDR algorithm

式(6)适用于前进行走和后退行走运动模式的航迹推算法，Lk为每一步的步长，θ为每一步的航向，Vk为高度差。Sk为运动模式标志，当前进行走时Sk=1，后退行走时Sk=-1，其他运动模式Sk=0。

3.2 横向航迹推算

图5 航迹推算算法模型Fig.5 Model for PDR algorithm

如图5所示为二维运动模型，当行人从A点前进行走到B点，再从B点左横向行走到C点，这个过程航向不变，E(k)减少了Lkcosθk，N(k)增加了Lksinθk；或行人从A点前进行走到B点，再从B点右横向行走到C′点时，航向同样不变，E(k)增加了Lkcosθk，N(k)减少了Lksinθk。如果使用传统的航迹推算算法，行人的位置会在D点，这与实际轨迹垂直，传统的航迹推算算法也不再适用。

当只考虑横向行走时，航迹推算算法改为

式中：Lk为每一步的步长，θ为每一步的航向，Vk为高度差；Uk为运动模式标志，左横向行走时Uk=-1，右横向行走时Uk=1，其他运动模式Uk=0。

3.3 多方位运动航迹推算

行人实际运动是包括前进行走、后退行走、左横向行走和右横向行走的多方位混合运动模式，本文提出的多方位运动航迹推算算法为

式中：Lk为每一步的步长，θ为每一步的航向，Vk为高度差，Sk为前、后行走运动模式标志，Uk为左、右横向行走运动模式标志。前进行走时，Sk=1，Uk=0；后退行走时，Sk=-1，Uk=0；左横向行走时Sk=0，Uk=-1；右横向行走时Sk=0，Uk=1；其他运动模式，Sk=0，Uk=0。Sk和Uk的值可以由方位识别确定。

3.4 方位识别

通过实验对比分析，当人体前进行走和后退行走时，加速度Y轴正弦波相位正好相差180°；左横向行走和右横向行走时，加速度X轴正弦波相位正好相差180°，即加速度值总是沿着行走方向先增大后减小。于是提出了相位反转法以区分4类运动模式，只需判断加速度X轴或Y轴的正弦波相位是0°还是180°即可[12]。

行人行走时手机X轴向右，Y轴指向前进方向，Z轴向下。如图6所示，前进和后退行走时Y轴的波形相位相差180°，加速度计Y轴输出波形先增大后减小是前进行走，先减小后增大是后退行走。

图6 Y轴波形Fig.6 Y-axis acceleration waveform

4 实验结果

本文选用重庆邮电大学标准足球场为测试地点，进行多方位运动的二维自主导航定位验证，行人手持智能手机围绕足球场行走一圈，即起点和终点重合。如图7所示，测试路线为，从A点前进行走到B点，接着从B点右横向行走到C点，然后从C点后退行走到D点，最后从D点左横向行走到A点。这时，可由行人的起点与终点的距离误差作为判断定位精度的标准，起点与终点的距离越小，就证明系统的定位精度越高。

图7 测试场景-足球场Fig.7 Test scenarios

图 8(a)是通过传统的航迹推算算法得到的轨迹图，图8(b)是通过本文提出的多方位运动自主导航定位算法轨迹图，可见，本文提出的多方位运动自主导航定位算法在多方位运动切换行走过程得到更可靠的定位信息。

选用重庆邮电大学第三教学楼进行三维定位测试，第三教学楼共5层，矩形走廊的长度为62 m，宽度为43 m。测试过程中行人从起点依次在每层楼行走，最终回到起点。通过对来自10个人的10组数据进行统计，如表1所示，本文提出的算法定位误差在3.2%以内，基本满足行人多方位运动三维自主导航需求。

图8 传统定位算法及本文改进算法定位结果对比Fig.8 Comparison on positioning results between traditional algorithm and improved algorithm

表1 测试结果Tab.1 Tracking results

5 结 论

针对传统行人航迹推算算法只能适用于单一前进行走运动模式的问题，分析了行人多方位运动的特征，提出了多方位运动模式三维自主导航算法。不仅提高了混合运动模式下步态检测的正确率，而且能够区分4个方位的运动模式。大大提高了定位的精度，达到 96.8%以上。因此，本文所提出的多方位运动模式三维自主导航定位算法可以真正有效地应用到人类实际的生活中，具有较好的应用价值。

（References）：

[1] 姬振龙. 低成本组合导航系统研究[D]. 上海: 上海交通大学, 2010. Ji Zheng-long. Research of low-cost integrated navigation system[D]. Shanghai: Shanghai Jiao Tong University, 2010.

[2] Nilsson J O, Zachariah D, Skog I, et al. Cooperative localization by dual foot-mounted inertial sensors and inter-agent ranging[J]. EURASIP: Journal on Advances in Signal Processing, 2013, 2013(1): 1-17.

[3] Li F, Zhao C, Ding G, et al. A reliable and accurate indoor localization method using phone inertial sensors[C]// Proceedings of the 2012 ACM Conference on Ubiquitous Computing. 2012: 421-430.

[4] Schindhelm C K. Activity recognition and step detection with smartphones: Towards terminal based indoor positioning system[C]//2012 IEEE 23rd International Symposium on Personal Indoor and Mobile Radio Communications. 2012: 2454-2459.

[5] 李昊. 基于三轴加速度传感器的动作分类和步数检[D].天津: 天津大学, 2010. Li Hao. Study of activities classify and step detection base on the three-dimensional acceleration sensor[D]. Tianjin: Tianjin University, 2010.

[6] Levi R W, Judd T. Dead reckoning navigational system using accelerometer to measure foot impacts: U.S., 5583776[P]. 1996-12-10.

[7] Zhang H, Zhang J, Zhou D, et al. Axis-Exchanged compensation and gait parameters analysis for high accuracy indoor pedestrian dead reckoning[J]. Journal of Sensors, 2015, 2015(2): 1-13.

[8] Xu Yuan, Chen Xi-yuan, Li Qing-hua, et al. Indoor pedestrian navigation based on double-IMU framework [J]. Journal of Chinese Inertial Technology, 2015, 23(6): 714-717.

[9] 刘宇, 江宏毅, 王仕亮, 等. 基于加速度时域特征的实时人体行为模式识别[J]. 上海交通大学学报, 2015, 49(2): 169-172. Liu Yu, Jiang Hong-yi, Wang Shi-liang, et al. Real-time human activity pattern recognition based on time domain features of acceleration[J]. Journal of Shanghai Jiaotong University, 2015, 49(2): 169-172.

[10] Kang W, Han Y. SmartPDR: smartphone-based pedestrian dead reckoning for indoor localization[J]. IEEE Sensors Journal, 2015, 15(5): 2906-2916.

[11] 钱伟行, 曾庆化, 万骏炜, 等. 基于人体下肢运动学机理的行人导航方法[J]. 中国惯性技术学报, 2015, 23(1): 24-28. Qian Wei-xing, Zeng Qing-hua, Wan Jun-wei, et al. Pedestrian navigation method based on kinematic mechanism of human lower limb[J]. Journal of Chinese Inertial Technology, 2015, 23(1): 24-28.

[12] 陈兴秀, 张金艺, 晏理, 等. 三维复杂运动模式航迹推算惯性导航室内定位[J]. 应用科学学报, 2014, 32(4): 349-356. Chen Xing-xiu, Zhang Jin-yi, Yan Li, et al. Inertial indoor navigation with 3D complex motion mode of pedestrian dead reckoning[J]. Journal of Applied Sciences, 2014, 32(4): 349-356.

Three-dimensional autonomous navigation algorithm based on multi-azimuth movement pattern

LIU Yu1, ZHOU Fan1, LI Yun-mei1, LU Yong-le1, PENG Hui2, ZHANG Xin1
(1. Chongqing Municipal Level Key laboratory of Photoelectronic Information Sensing and Transmitting Technology, Chongqing University of Post and Telecommunications, Chongqing 400065, China; 2. The 26th Institute of China Electronics Technology Corporation, Chongqing 400065, China)

The pedestrian navigation based on MEMS sensor usually achieves real-time pedestrian positioning by using pedestrian dead reckoning (PDR) algorithm to calculate the coordinate of pedestrian’s position. Traditional PDR only considers forward movement pattern, which is not applicable to the actual multi-azimuth human movement pattern. Hence, a novel algorithm of three-dimensional autonomous navigation based on multi-azimuth movement pattern is proposed by using the data of three-axis accelerometer to implement step detection and stride-length estimation. Based on the analysis of the accelerometer data, a pattern recognition method for four types of movement patterns is discussed, and the dead reckoning equation applied to pedestrian multi-azimuth movement pattern is derived. Verification experiments are made on smartphone platform by using the proposed algorithm into the actual autonomous navigation based on multi-azimuth movement pattern, which show that the positioning error is less than 3.2%, significantly improving the navigation accuracy.

MEMS sensor; three-dimensional autonomous navigation; dead reckoning; multi-azimuth

U666.1

：A

2016-04-27；

：2016-06-30

国家自然科学基金资助项目（51175535）；国际联合研究中心科技平台与基地建设（cstc2014gjhz0038）；重庆市基础与前沿研究计划项目（cstc2015jcyjBX0068）

刘宇（1972—），男，硕士生导师，教授，主要从事惯性导航及传感器件的研究。E-mail: mianfeiyangpian@163.com

1005-6734(2016)04-0449-05

10.13695/j.cnki.12-1222/o3.2016.04.006