一种新型稳定平台伺服控制系统
2016-04-19王立玲李保宗刘秀玲肖金壮王光磊王洪瑞
王立玲,李保宗,刘秀玲,肖金壮,王光磊,王洪瑞
(河北大学电子信息工程学院 河北省数字医疗工程重点实验室,河北 保定 071002)
一种新型稳定平台伺服控制系统
王立玲,李保宗,刘秀玲,肖金壮,王光磊,王洪瑞
(河北大学电子信息工程学院 河北省数字医疗工程重点实验室,河北 保定 071002)
深入研究了三自由度并串联混合机构稳定平台,设计了一个非线性自适应控制器。考虑到实际系统工作中存在摩擦、负载扰动和动力学参数误差,分离出动力学模型中的未建模动力学参数、摩擦力参数和负载扰动,建立了关于待辨识参数的线性动力学模型。运用 Lyapunov方法设计了一个非线性自适应控制器。构建了并串联光电稳定平台伺服系统实验平台。分别将所设计的控制器与计算力矩控制器分别在高速和低速扰动情况进行了实验,实验表明所提出非线性自适应控制器在低速0.006 (°)/s时,跟踪精度分别为滚转轴0.071°、俯仰轴0.064°、偏转轴0.038°,在20 (°)/s高速状态下,跟踪精度分别为滚转轴0.045°、俯仰轴0.042°、偏转轴0.029°,其控制效果明显好于传统控制。
并串联机构;动力学分析;非线性自适应控制;惯量矩阵
稳定平台的作用通过多种传感器在线检测,实时跟踪控制系统来隔离外界载体的扰动,为载体上的设备或人员提供一个稳定的工作平台。其控制技术涉多学科的知识。目前在实际使用的主要是隔离载体的二、三轴摇摆的串联旋转台,在小负载时能快速跟踪目标[1]。与目前存在的串联式稳定平台机构相比,并联机构的动力设备可以安装机架的位置。工作的运动台一般是几个运动链与机架相联接。因此其机构占的空间小、刚度强、承载力高。并联机构本体尺寸变化很大时,仍保持非常稳定的动力学特性。并联机构反解简单,但正解比较复杂。并联机构各个连杆间耦合性强、工作空间窄小[2]。串并联机构综合了串联机构和并联机构的共同优点,不仅克服了原有并联机构工作空间小的缺点,获得了较大的工作空间,而且克服了原有串联机构刚度小、承载能力不足等缺点。既具有并联机构刚度大、误差小、自重负荷比小、运动惯性小、动力性能好、控制容易等特点,同时又具有较大的工作空间和灵活度,因此具有很好的应用前景[3]。
本文研究一种新型三自由度并串联光电稳定平台系统,考虑实际系统工作中存在的摩擦、负载扰动和动力学参数误差,采用非线性自适应理论设计了控制系统。通过搭建实验系统,实验研究非线性自适应控制策略在实际并串联光电稳定平台实验装置上的跟踪效果和跟踪性能。
1 基于动力学模型的非线性自适应控制器设计
并串联光电稳定平台如图1所示,由正交球面并联机构和与之串联的旋转台构成,其中二自由度球面并联机构为空间5杆机构,所有运动副均为转动副,所有轴线皆汇交于一点O,电机1和电机2轴互相垂直。二自由度球面并联机构运动平台只做围绕球心O的转动。电机3与工作台直接相连,电机3的轴线垂直于该工作平台。
基坐标系为ob-xbybzb,xb与电机1轴线一致,yb与电机 2轴线一致,zb由右手螺旋法则确定,动坐标系为om-xmymzm,xm和ym轴与OA和OC同轴,zm由右手螺旋法则确定,S1为沿OmA的单位矢量,S2沿OE的单位矢量,S3沿OC的单位矢量。机构输入为电机转角θ1、θ2,绕xb轴旋转为滚转角θr,绕yb轴旋转为俯仰角θp,输出上平台姿态即为滚转角θr、俯仰角θp。

图1 并串联光电稳定平台Fig.1 Parallel-serial photoelectric stabilized platform
考虑到摩擦力、负载扰动和动力学特性的非线性以及不确定性,本文选取相应的动力学参数、摩擦力模型中的参数和负载扰动作为自适应参数,从稳定平台动力学模型中分离出这些自适应参数,把非线性强耦合的动力学模型写为关于待辨识参数的线性表达式。
为了提高伺服系统的跟踪性能,在系统运行过程中,实时估计系统模型参数以及非线性摩擦模型参数,进行自适应摩擦补偿控制[4-6]。考虑到机构在速度变化时,其摩擦力参数和特性将发生较大变化,选取自适应参数中包括了连杆之间的库仑摩擦力和粘滞摩擦力系数,从而在自适应控制的过程中实现摩擦力的自适应补偿。
摩擦力fm定义为

式中,fci表示库仑摩擦力,fvi表示粘滞摩擦力系数。
考虑负载扰动和系统摩擦力的串并联稳定平台的动力学模型如下:

式中,M(θ)为3×3惯量矩阵,B(θ)为3×3的哥氏力系数矩阵,C(θ)为3×3的离心力系数矩阵,。要实现有效的动力学控制,必须知道动力学模型(2)中相关参数的精确值。但是一方面,当机构装配好后,其动力学参数难以精确测量,并且会受负载的影响;另一方面,机构在运动过程中所受的摩擦力存在复杂的非线性,且摩擦力特性受速度的影响很大。所定义的库仑+粘滞摩擦力模型式(1),其模型参数的值在不同运动速度下也会发生波动。所以,需要通过在线辨识动力学参数和摩擦力模型中的参数来实时计算动力学补偿项和摩擦力补偿项,从而实现稳定平台的自适应控制。
1.1 稳定平台动力学模型
要实现并联机构的自适应控制,首先必须在线辨识出自适应参数,即未建模部分,根据动力学模型中各个项所占比重,在考虑未建模和测量精度和装配误差等原因,惯量矩阵修正为
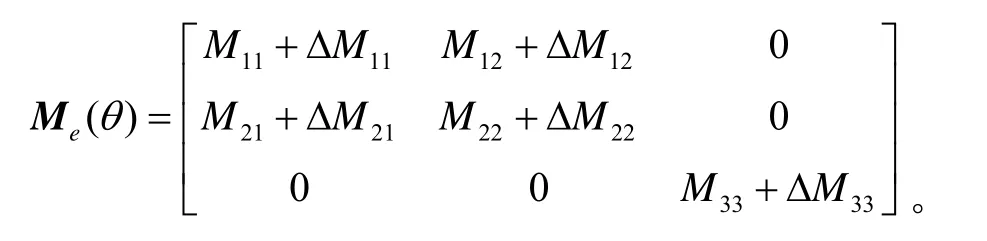
把待辨识的参数从动力学模型(2)中分离出来,从而把动力学模型写成关于待辨识参数的线性表达式:

式中,待辨识参数a是一个12×1的向量,它包含了3个动力学参数ΔM11、ΔM12、ΔM22以及3个扰动f1、f2、f3和摩擦力模型中的6个参数fci、fvi(i=1,2,3)。在式(3)中,是3×12的回归矩阵。
1.2 非线性自适应控制器设计
1.2.1 控制律设计
设θd为末端执行器在工作空间的期望轨迹,实际位置跟踪误差e定义为

定义广义误差向量s为

式中,Λ为对称正定矩阵。事实上,s≡0代表了一个线性微分方程组,假定θd(0)=θ(0),则其唯一解是e≡0。因此e和同时收敛的问题可以简化为使s趋近于0的问题。在式(5)的基础上定义为


基于动力学模型,设计如下的控制律:
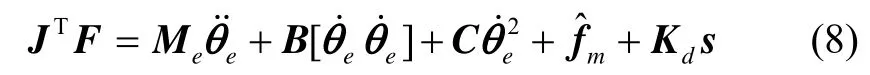
式中,Me是由动力学修正参数计算得到惯性矩阵,为由摩擦力自适应辨识参数计算得到的摩擦力,Kd为对称正定矩阵。

在控制律(9)中,F代表操作空间的控制力矩,而实际控制需要的是三个主动关节的驱动力矩:

控制律(9) 实际上是由系统估计矩阵Me摩擦力估计值以及常量矩阵Kd和Λ共同决定的,Me由辨识得到的动力学参数计算得到,由辨识得到的摩擦力参数计算得到,因此下面将讨论如何获得这些待辨识参数。
1.2.2 参数自适应律设计
控制律(8)中的动力学补偿项、摩擦力补偿项和负载扰动可写为

1.2.3 系统稳定性分析
定理1:设计的控制律(8)和参数自适应律可以使得并串联光电稳定平台伺服系统(2)的稳定性,t→∞时,e→0和→0。


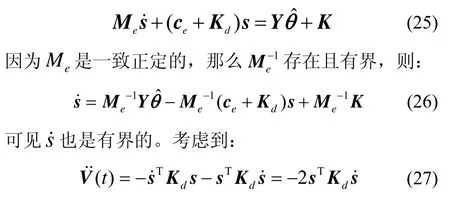

图2 非线性自适应控制方框图Fig.2 Configuration of nonlinear adaptive control system
2 伺服系统电气设计
并串联光电稳定平台实验系统的电气控制系统,由电气控制柜、伺服控制系统和电源部分等组成。伺服控制系统主要对来自上位计算机、陀螺仪的指令、状态和误差信号进行综合、校正等处理形成驱动伺服平台。电机转动的控制电压来完成对台体的操作和控制,实现并串联光电稳定平台上成像传感器视轴的稳定和对目标的跟踪。稳定平台的伺服系统总框图如图3所示。

图3 稳定平台的伺服系统框图Fig.3 Block chart of a stable platform’s servo system
3 实验及结果
3.1 实验设计
实验硬件平台如图 4所示,位于下面的是正交3-2-1结构六自由度并联运动平台,模拟载体运动用于提供扰动。位于上面的并串联光电稳定平台。六自由度运动平台和稳定平台分别由各自的电机驱动。
根据实际检测条件,本系统稳定精度的实验及测试方法是并串联光电稳定平台上安装惯性速率陀螺和倾角传感器以提供空间角速度和角度反馈。伺服控制系统通过对载体角运动的隔离以获得工作台保持惯性基准面。
计算机中安装Quarc软件后,采用QuaRC Targets中的各模块在Simulink中搭建控制器,通过NI6230板卡实现伺服控制算法和并串联光电稳定平台通信。并串联光电稳定平台的倾角传感器、光纤陀螺仪和编码器的电信号通过读模拟量(HIL Read Analog)模块读入到伺服控制器,控制信号通过写模拟量(HIL Write Analog)模块输出。

图4 并串联稳定平台实验系统Fig.4 Testing system of parallel-serial platform
3.2 实验结果
本节将所设计非线性自适应控制和传统计算力矩控制策略应用到并串联稳定平台上,进行对比实验。实验时给定输入为零,分别给六自由度运动平台电机施加12sin(2πt)(°)/s和20sin(2πt)(°)/s信号,模拟环境扰动。并串联稳定平台系统各转动轴运动实时位置实验数据曲线如图5至图7所示。图5至图7中,(a)图为12sin(2πt) (°)/s扰动时误差,(b)图为20sin(2πt) (°)/s扰动时误差。
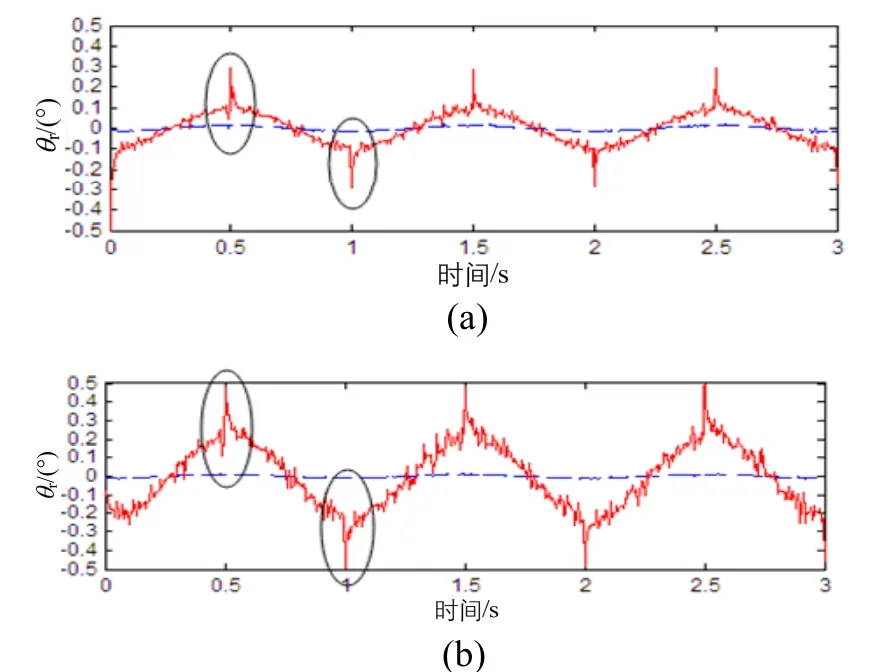
图5 滚转轴稳定误差Fig.5 Stabilized error of roll axis

图6 俯仰轴稳定误差Fig.6 Stabilized error of pitch axis

图7 偏转轴稳定误差Fig.7 Stabilized error of yaw axis
3.3 实验结果分析
由图5至图7可以看出,计算力矩控制时,滚转轴误差最大,横滚最小。非线性自适应控制时没有明显变化,滚转轴受俯仰轴耦合影响,在并串联光电稳定机构实际设计中,只要转动惯量变化范围不超过一定范围,就可以把转动惯量的变化当作一种扰动,通过控制系统的适当设计可以克服这种扰动对滚转轴的耦合影响。非线性自适应控制器能够通过在线辨识出俯仰对滚转的耦合未建模部分,并进行补偿。非线性自适应控制由于能够在反馈抑制干扰的基础上,在线辨识摩擦力、负载扰动和模型误差,并通过补偿进一步抑制,因此对摩擦的抑制能力明显优于计算力矩控制,基本上不存在尖峰误差。
从实验结果可以看出,并串联稳定平台采用计算力矩控制时,在低速的情况下,系统的跟踪误差相对较低,而在速度相对较大的情况下,系统的跟踪误差相对较大。总体而言,采用非线性自适应控制系统:1)在0.06 (°)/s时,滚转轴的跟踪精度为0.071°,俯仰轴跟踪精度为0.064°,偏转轴跟踪精度为0.038°;2)在20 (°)/s时,滚转轴的跟踪精度为0.045°,俯仰轴跟踪精度为0.042°,偏转轴跟踪精度为0.029°。这些结果显示了非线性自适应控制器的优良性能。
4 小 结
本文根据并串联稳定平台伺服控制系统要求,将所设计的非线性自适应控制应用于并串联光电稳定平台系统实验装置中。通过并联六自由度运动平台模拟实际载体扰动,与计算力矩控制实验结果对比研究,非线性自适应控制器能够在线辨识动力学未建模参数、摩擦力、各轴之间耦合,并实施补偿。无论低速还是高速,与计算力矩相比,在所有干扰补偿之后,系统稳定误差减小,证明了补偿的有效性,同时为工程应用提供了理论依据。
基于开放式结构、标准模块化的多功能运动平台伺服系统的建立,为光电稳定跟踪系统相关技术的研究和验证提供了一个有效的、与实际系统比较相似的模拟环境,所设计的实验平台能够在实验室条件下模拟船载、机载光电成像跟踪系统等动力学特性和空间运行姿态,为进一步研究宽频带、高性能的此类伺服系统的精度提供了良好的平台,可为实际系统的研制和改进提供参考依据和实验数据。
(References):
[1] Tanev T K. Kinematics of a hybrid (parallel-serial) robot manipulator[J]. Mechanism and Machine Theory, 2000, 35(9): 1183-1196.
[2] Chen C T. Reconfiguration of a parallel kinematic manipulator for the maximum dynamic load-carrying capacity [J]. Mechanism and Machine Theory, 2012, 54: 62-75.
[3] Patel Y D, George P M. Parallel manipulators applica-tions - a survey[J]. Modern Mechanical Engineering, 2012, 2(3): 57-64.
[4] Niu X M, Gao G Q, Liu X J, et al. Dynamics and Control of a Novel 3-DOF Parallel[J]. International Journal of Automation and Computing, 2013, 10(6): 552-562.
[5] Kokotovi P, Arcak M. Nonlinear and adaptive control: an abbreviated status report[R]//The 9th Mediterranean Conference on Control and Automation. Dubrovnik Croatia, 2001: 1-15.
[6] Niu X M, Gao G Q, Liu X J, et al. Dynamics and Control of a Novel 3-DOF Parallel[J]. International Journal of Automation and Computing, 2013, 10(6): 552-562.
[7] 任彦, 刘正华. 滑模自适应控制在光电稳定平台中的应用[J]. 控制工程, 2014, 21(1): 32-40. Ren Yan, Liu zheng-hua. Sliding mode adaptive control in the application of the photoelectric stabilized platform [J]. Journal of Control Engineering, 2014, 21(1): 32-40.
[8] 杨蒲, 李奇. 三轴陀螺稳定平台控制系统设计与实现[J].中国惯性技术学报, 2007, 15(2): 171-176. Yang Pu, Li Qi. Design and realization of control system for three-axis gyro stabilized platform[J]. Journal of Chinese Inertial Technology, 2007, 15(2): 172-176.
[9] Ansarifar G R, Talebi H A, Davilu H. An adaptivedynamic sliding mode controller for non-minimum phase systems[J]. Commun Nonlinear Sci Numer Simulut, 2012, 17(1): 414-425.
[10] Zheng Yun-feng, Wen Chang-yun, Li Zheng-guo. Robust adaptive asymptotic tracking control of uncertain nonlinear systems subject to nonsmooth actuator nonlinearities[J]. International Journal of Adaptive Control and Signal Processing, 2013: 108-121.
[11] Zhu Y, Wen C, Su H, et al. Adaptive modular control for a class of nonlinear systems with unknown time-varying parameters[C]//Proceedings of American Control Conference, Washington, USA, 2013: 17-19.
Servo control system for a new stabilized platform
WANG Li-ling, LI Bao-zong, LIU Xiu-ling, XIAO Jin-zhuang, WANG Guang-lei, WANG Hong-rui
(Key Laboratory of Digital Medical Engineering of Hebei Province, College of Electronic and Information Engineering, Hebei University, Baoding 071002, China)
A parallel-serial opto-electronic stable platform was developed, and a nonlinear adaptive controller was designed. Considering that there were friction, load disturbance and kinetic parameters error in the real controller system, the unmodeled dynamics parameters, friction parameters and effects of load disturbance were separated from the dynamics model. Then the dynamic model with linear expressions was established. A Lyapunov method was applied for the design of nonlinear adaptive controller. The new proposed nonlinear adaptive controller was applied into the parallel-serial opto-electronic stable platform under the disturbances of high speed and low speed, respectively. The analysis and experiment results show that, by using the proposed nonlinear adaptive controller, the tracking precisions of rolling axis, pitching axis and yaw axis are 0.071°, 0.064° and 0.038° respectively in low-speed condition of 0.006 (°)/s, and they are 0.045°, 0.042° and yaw axis 0.029° respectively in high-speed condition of 20 (°)/s. The control effects of the nonlinear adaptive controller are significantly better than those of traditional computed torque controller.
parallel-serial mechanism; dynamics analysis; nonlinear adaptive control; inertia matrix
U666.1
:A
2016-03-25;
:2016-05-30
国家自然科学基金资助项目(61473112 );河北省教育厅青年基金资助项目(QN2014101);河北省自然科学基金项目(F2015201112)
王立玲(1979—),女,博士,从事并联机构的动力学建模与控制研究。E-mail: wll_betty@126.com
1005-6734(2016)04-0431-06
10.13695/j.cnki.12-1222/o3.2016.04.003
