抗差自适应滤波的导向钻具动态姿态测量方法
2016-04-19汪跃龙程为彬
高 怡,汪跃龙,程为彬
(1. 西安石油大学 陕西省油气井测控技术重点实验室,西安 710065;2. 西安石油大学 电子工程学院,西安 710065)
抗差自适应滤波的导向钻具动态姿态测量方法
高 怡1,2,汪跃龙1,2,程为彬1,2
(1. 西安石油大学 陕西省油气井测控技术重点实验室,西安 710065;2. 西安石油大学 电子工程学院,西安 710065)
针对钻井工程中,导向钻井工具在近钻头振动条件下,由于底部钻具振动对导向工具姿态测量造成严重干扰,使得姿态参数失真,导致姿态测量不准确的问题。为了消除或削弱振动对空间姿态测量的不利影响,快速解算出准确的钻具姿态参数,提出一种抗差自适应滤波的动态姿态测量方法,利用等价权函数和自适应因子合理的分配信息,有效地滤除钻具振动对动态姿态测量的影响。仿真实验和实钻井数据试验证明,采用该算法能滤除近钻头振动干扰信号,井斜角控制在5.5°左右,工具面角测量误差小于6°,有效地提高了导向钻井工具姿态参数的动态测量精度,解决动态测量时姿态参数测不准的问题。
导向钻井;动态测量;钻具振动;抗差估计;自适应滤波
随着石油工业的不断发展和油气勘探开发难度的增大,国内外竞争也愈来愈激烈。载体空间姿态测量在石油工业领域中的地位也越来越显赫。这就意味着,对姿态参数(井斜角、工具面角和方位角)测量的实时性、精确性以及连续、动态测量的要求也越来越高[1-2]。井下动态空间姿态参数的实时测量是导向工具实现实时导向控制的前提条件。然而,在实际钻井工程中,由于底部钻具振动对导向工具姿态测量造成严重干扰,使得姿态参数严重失真,导致姿态测量不准确。目前普遍采用随钻测量(Measurement While Drilling,MWD)技术对井下姿态进行测量。该方法虽然能得到准确的姿态参数,但要求姿态测量时必须停止钻进,属于静态测量,存在时效低、成本高和风险大等问题。如何在不停钻条件下获得实时性强、精度高的连续动态姿态测量,是目前该方向的研究热点及难点之一。
文献[3]提出了一种采用卡尔曼滤波的新状态空间法连续实时测量钻井轨迹,针对旋转导向钻井和自动垂直钻井建立一套捷联测量系统[4],采用卡尔曼滤波估计系统状态,但是该方法没有考虑测量传感器信号中包含的大量振动加速度。杨全进等提出一种新的旋转导向钻井动态位置测量方法[5],介绍了常用的石油钻井定向传感器的结构和测量参数,提供了一种在钻柱旋转情况下的动态位置测量技术,详细分析了如何计算实时精确的重力工具面角。采用无迹卡尔曼滤波方法消除传感器数据中的干扰噪声,提高旋转导向钻具姿态测量的准确性[6]。徐宝昌等在此基础上又提出了一种旋转导向系统有色噪声的改进无迹卡尔曼滤波方法。该方法利用四元数理论构造观测方程和时变状态方程,实时解算出钻具姿态,有效的滤除了加速度传感器数据中的有色噪声[7]。但是该算法限制条件较多,只是将钻具轴向振动信号作为主要干扰进行分析。Elgizawy和Jurkov等提出一种基于惯性导航系统的测量井斜与方位角的传感器封装,通过仿真验证基于惯性导航的传感器封装可以实现高精度连续MWD测量[8-10]。Yanshun等人基于简易惯性单元开发了一种相似的MWD装置[11]。由于井下工况复杂,钻柱旋转向下运动常伴随着各种振动现象,钻具振动严重影响了传感器的测量精度,导致测量误差较大。
在上述研究的基础上,针对导向钻井工具动态测量受钻具振动的影响而导致测量不准确的问题,提出一种抗差自适应滤波的动态空间姿态测量方法。通过分析钻具振动对姿态测量的影响,并吸收抗差估计和自适应滤波的优点,利用抗差等价权矩阵自适应的确定量测信息,通过自适应因子调整状态模型信息对状态参数的整体贡献,从而消除钻具振动对动态姿态测量的影响,获得实时性强、精度高的姿态参数,提高钻井效率,降低钻井风险。
1 钻具振动对姿态测量的影响
钻井振动与钻柱及其组成部分的动力特性相关,通过监测钻柱的动力特性,削弱振动对钻井测量的影响,可以有效的提高钻井效率,降低钻井事故,因此,钻井的振动问题成为目前的研究热点之一。
在实际钻井过程中,钻头切削岩层、钻柱与井壁的碰撞等会使钻具产生横向振动、纵向振动和扭转振动等,这些振动严重的影响了测量传感器输出信号的正确性。而横向振动又是石油钻井下部钻具(钻头及近钻头钻铤和钻杆)的主要振动形式之一[12]。章杨烈指出横向振动对钻具的损害大于纵向振动和扭转振动[13]。采用常用的牙轮钻头进行钻进,钻具横向振动具有较强的随机性,其强度属于剧烈分区,近钻头横向振动强度随钻压、钻速增大而增大。钻头振动信号是一种非稳态连续随机振动,具有较宽的频带,影响因素复杂。
钻柱的横向振动的传播方程如下:

式中:ρ表示钻柱质量密度,A表示钻柱横截面积,ω表示钻柱微元偏离井眼轴线的横向位移,z为轴向坐标,S为源于X方向的剪切力,fF为外部力。

式中:力矩M为

设弹性模量为E,横截面积对中性轴的惯性矩为I。
将式(2)和(3)代入到式(1)中,得到关于横向振动的传播方程:

根据上述动力学方程即可对钻具横向振动的传播进行数值模拟。
在导向钻井系统的动态空间姿态测量时,由于三轴磁通门数据中包含磁干扰,三轴加速度计测量数据中包含大量的振动加速度,严重影响组合钻具井斜及方位姿态测量精度。为了研究井下振动对姿态测量信号的影响,通过分析横向振动信号特性,根据横向振动的传播方程,井下钻具横向振动加速度响应曲线如图1所示。
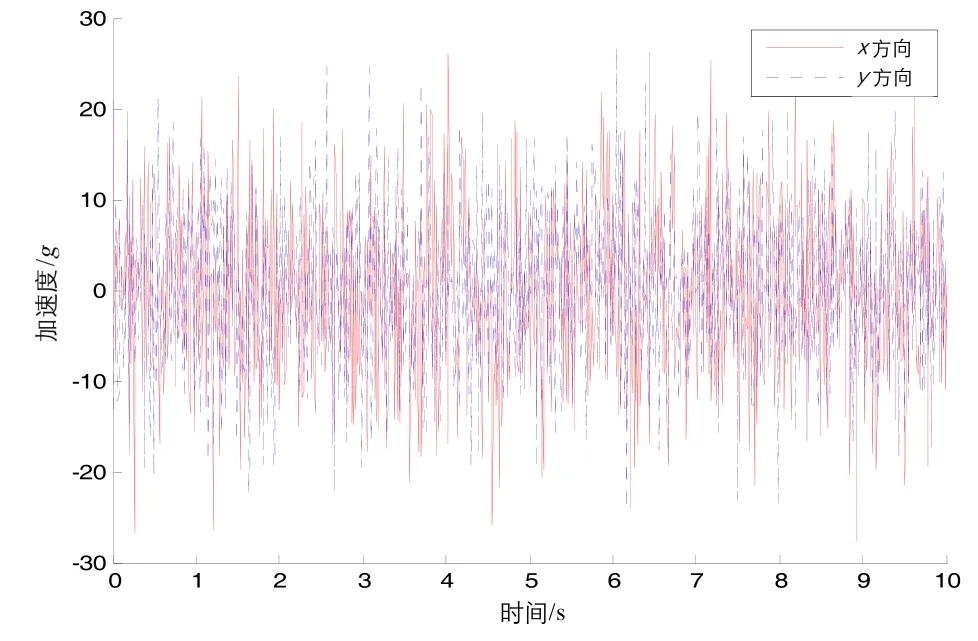
图1 钻具横向振动加速度响应曲线Fig.1 Transverse vibration acceleration response curve of drilling tool
2 抗差自适应滤波动态测量姿态解算
抗差自适应滤波的基本思想是当观测值存在异常时,对观测值采用抗差估计原则,能够控制观测异常的影响;当动力学模型存在异常误差时,将动力学模型信息作为一个整体,采用统一的自适应因子调整动力学模型信息对状态参数的整体贡献[14-16]。
2.1 导向钻井工具姿态测量系统动态建模
选取地理坐标系以“东北天(ENU坐标系)”为顺序构成的右手直角坐标系,即E轴沿当地水平面指向东,N轴沿当地水平面指向北,U轴沿当地垂线指向上。再以钻具三个基本轴建立钻具坐标系(XYZ坐标系),取Z轴和钻具的轴线方向一致,X轴和Y轴在同一水平面内且互相垂直,Z轴跟二者垂直并构成右手直角坐标系。
在以上选取的坐标系下,各姿态角如图2所示,其中,H为水平面,V为钻孔弯曲平面,P代表钻具横截面。方位角ψ为磁北方向沿逆时针方向到Z轴在水平面的投影间的夹角,其范围在 0°~360°之间,井斜角θ为钻进轴Z轴与水平面所成的夹角,规定向下为正,反之为负,其范围为-90°~90°,工具面向角γ则为钻孔横截面内由钻孔高边到Y轴所成的角度,范围在 0°~360°之间。这样,我们就准确的定义了井下钻具的方位角ψ、井斜角θ和工具面向角γ,且角度的正向都符合右手系原则。
根据导航理论中的欧拉定理,载体在空间中的姿态可用相对于地理坐标系有限次的转动来表示,每次转动的角度即为航向角、俯仰角和横滚角。同理,井下钻进过程中,钻具在空间的任一姿态都可以用相对于地理坐标系的一系列旋转来表示,旋转的角度为方位角、倾角和工具面向角。在XYZ坐标系中安装三轴加速度计和三轴磁通门,如图3所示。

图2 坐标系中表示的姿态角Fig.2 Attitude angles in a coordinate system

图3 加速度计和磁通门组合测量安装示意图Fig.3 Combined measurements of accelerometer and fluxgate
设Gx、Gy和Gz分别为地球重力加速度g向钻具坐标系上投影:

由式(5)可以解算得到井斜角和工具面角为

根据上述理论,建立导向钻井工具姿态测量的动态数学模型,给出状态方程和量测方程。
假定tk时刻的动力学模型方程为

式中:xk和xk-1分别为tk和tk-1时刻的n维状态参数向量,为n×n维状态转移矩阵;wk为p维动力学模型误差向量,其数学期望为0,协方差矩阵为

显然,wk为高斯白噪声序列。
设tk时刻的量测方程为
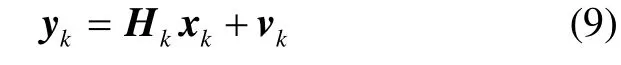
式中:yk为tk时刻的m维观测向量;Hk为m×n维测量矩阵,也称为观测矩阵;vk为m维观测误差向量,其数学期望为0,协方差矩阵为

显然,vk为高斯白噪声序列。在i=k时,的协方差矩阵分别为互不相关。
状态向量为

式(9)表明直接将钻具姿态参数作为状态向量,而非姿态误差作为状态。
当钻具坐标系相对地理坐标线加速度为零的情况下,三轴加速度计的输出记为即此时钻具坐标系的加速度输出也就是地球的重力加速度g在钻具坐标系上的投影。三轴磁通门的输出记为
将加速度计、磁通门测量值与当地重力场、磁场强度在钻具坐标系下投影的差值作为量测,共6维,则量测方程如下

式中:ya三轴加速度计测量时输出数据矩阵,ym为磁强计测量值;G为重力场,G=[00g]T;M为磁力场,M=[M10M2]T,M1和M2分别为地理坐标系中地磁场北向分量和垂直分量的测量值,M1=ξcosθ,M2=ξsinθ,ξ为当地地磁强度;C为姿态旋转矩阵,。
2.2 导向钻井工具抗差自适应滤波的动态姿态测量
采用抗差自适应滤波器实现各传感器数据融合,计算导向钻具工具姿态测量的框图如图4所示,其中,ψ、θ和γ分别为方位角、井斜角和工具面角。

图4 姿态参数估计框图Fig.4 Attitude parameter estimation
考虑模型式(7)和(9),系统状态预测向量为

式中:Vk为观测残差向量,为预测残差向量。Vk和的协方差矩阵分别为

合理地选择自适应因子不但能够自适应地平衡动力学模型预测信息与量测信息的权比,而且能够控制动力学模型扰动异常对滤波解的影响。基于预测残差误差判别统计量的抗差自适应因子函数为


等价权矩阵为
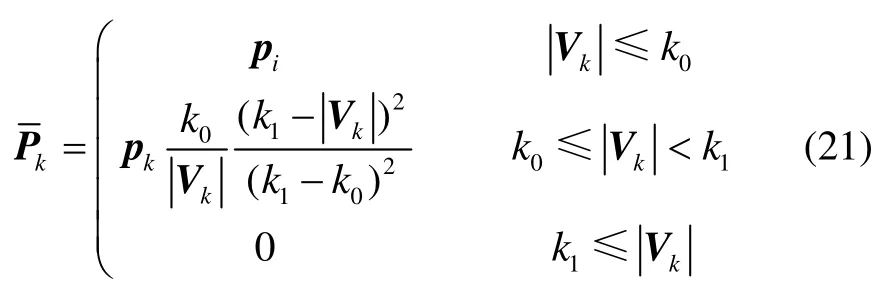
式中:k0∈(1,1.5),k1∈(3,8),Vk为观测值的残差向量。
由式(14)~(16)和式(19)~(21)可构造如下极值:

式中:Kk为增益矩阵,根据矩阵恒等式,可表示为

对量测信息采用抗差估计,自适应的确定观测噪声协方差矩阵,并利用自适应因子调节状态噪声的协方差矩阵,因此,可以有效的控制量测异常和动态模型噪声异常对空间状态参数估值的影响。
3 实验及分析
3.1 数值计算仿真及分析
实验室地理条件为北纬34.24°,东经108.99°,地球自转角速度为 15 (°)/h,磁倾角为 55.4°,磁场强度为52.5 μT,地球重力加速度为9.8 m/s2。在实验室条件下,根据测斜校验装置测量得到一组理想的实验数据。
将模拟振动试验中得到的三个加速度输出信号经过解算后送到抗差自适应滤波器中进行滤波处理,得到滤波前后的井斜角和工具面角对比曲线分别如图 5和图6所示。

图5 数值计算滤波前后井斜角对比曲线Fig.5 Contrast curves of deviation angles before and after filtering by numerical calculation

图6 数值计算滤波前后工具面角对比曲线Fig.6 Contrast curves of tool face angles before and after filtering by numerical calculation
从图5和图6中可以非常直观地看到,经过抗差自适应滤波处理后的井斜角和工具面角波动范围明显变小,滤波后的数据曲线更加平滑,横向振动干扰信号基本滤除,滤波效果明显。
3.2 实钻井数据试验及分析
为了进一步验证算法的有效性,采用实钻井数据进行试验和分析,分别对提出的抗差自适应滤波算法与卡尔曼滤波(KF)算法进行对比。
实验数据来源于 2012年陕北某井的实钻井过程中的某一段数据,钻井深度为1876m,钻速为45m/h,钻压1~10 t,温度40℃。
从图7和图8可以看出,滤波前井斜角和工具面角波动较大,采用卡尔曼滤波器后井斜角误差仍较大,而经过抗差自适应滤波器后,井斜角控制在5.5°左右,与静态测量下测得的井斜角基本相同。工具面角经过滤波后曲线更加平滑,干扰信号基本滤除,工具面角误差小于 6°。实验结果表明,提出的抗差自适应滤波能够抑制横向振动对导向钻井工具动态姿态测量的影响。

图7 实钻井数据滤波前后井斜角对比曲线Fig.7 Contrast curves of deviation angles before and after filtering by real drilling data calculation

图8 实钻井数据滤波前后工具面角对比曲线Fig.8 Contrast curves of tool face angles before and after filtering by real drilling data calculation
4 结 论
针对近钻头强振动对姿态参数所造成的测不准问题,提出采用抗差自适应滤波方法来减小近钻头强振动对导向钻井工具姿态参数测量的影响。从横向振动传播方程着手,根据振动干扰信号特性,设计了针对性的模拟振动实验。分析振动加速度为姿态测量的影响,通过抗差自适应滤波器有效地滤除近钻头振动信号,解决导向钻井工具姿态参数的动态测量问题,提高了导向钻井工具姿态测量的准确性。
这里只是考虑了钻具的横向振动对导向钻井工具姿态测量的影响,没有考虑纵向振动和扭转振动的影响,下一步工作考虑如何对这两种振动进行模拟,采用更合适的滤波算法消除干扰信号,以期获得更精确的动态测量姿态参数。
(References):
[1] 薛启龙, 丁青山, 黄蕾蕾. 旋转导向钻井技术最新进展及发展趋势[J]. 石油机械, 2013, 41(7): 1-6. Xue Qi-long, Ding Qing-shan, Huang Lei-lei. The latest progress and development trend of rotary steering drilling technology[J]. China Petroleum Machinery, 2013, 41(7): 1-6.
[2] 汪跃龙, 王海皎, 康思民, 等. 导向钻井稳定控制平台的反馈线性化控制[J]. 石油学报, 2014, 35(5): 952-957. Wang Yue-long, Wang Hai-jiao, Kang Si-min, et al. Output feedback linearization of servo platform for rotary steering drilling system[J]. Acta Petrolei Sinica, 2014, 35(5): 952-957.
[3] Xue Qi-long, Leung H, Wang Ruihe, et al. Continuous real-time measurement of drilling trajectory with new state space models of kalman filter[J]. IEEE Transactions on Instrumentation and Measurement, 2016, 65(1): 144-154.
[4] 薛启龙, 王瑞和, 孙峰, 等. 捷联式旋转导向井斜方位动态解算方法[J]. 中国石油大学学报(自然科学版), 2012, 36(2): 93-97, 107. Xue Qi-long, Wang Rui-he, Sun Feng, et al. Dynamic solution approach to inclination and azimuth of strapdown rotary steerable system[J]. Journal of China University of Petroleum, 2012, 36(2): 93-97, 107.
[5] Yang Quan-jin. A new method for dynamic position measurement while drilling string rotating[J]. Applied Mechanics and Materials, 2012(152-154): 1102-1105.
[6] 杨全进, 徐宝昌, 左信, 等. 旋转导向钻具姿态的无迹卡尔曼滤波方法[J]. 石油学报, 2013, 34(4): 1168 -1175. Yang Quan-jin, Xu Bao-chang, Zuo Xin, et al. An unscented Kalman filter method for attitude measurement of rotary steerable drilling assembly[J]. Acta Petrolei Sinica, 2013, 34(4): 1168-1175.
[7] 徐宝昌, 杨全进, 蒋海旭. 旋转导向系统有色噪声的改进无迹卡尔曼滤波方法[J]. 中国石油大学学报(自然科学版), 2015, 39(2): 157-163. Xu Bao-chang, Yang Quan-jin, Jiang Hai-xu. Improved unscented Kalman filtering method for colored noises of rotary steerable system[J]. Journal of China University of Petroleum, 2015, 39(2): 157-163.
[8] Elgizawy M, Noureldin A, Georgy J, et al. Wellbore serveying while drilling based on kalman filtering[J]. American Journal of Engineering and Applied Sciences, 2010, 3(2): 240-259.
[9] Elgizawy M, Noureldin A, El-Sheimy N. Continuous wellbore surveying while drilling utilizing MEMS gyroscopes based on Kalman filtering[C]//Proceedings of 2010 SPE Annual Technical Conference & Exhibit. Florence, Italy, 2010: 5416-5428.
[10] Jurkov A S, Cloutier J, Pecht E, et al. Experimental feasibility of the in drilling alignment method for inertial navigation in measurement while drilling[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(3): 1080-1090.
[11] Zhang Yanshun, Wanf Shuwei, Fang Jiancheng. Measurement while drilling instrument based on predigested inertial measurement unit[J]. IEEE Transactions on Instrumentation and Measurement, 2012, 61(12): 3295-3302.
[12] 祝效华, 胡志强. 基于钻头破岩钻井的下部钻具横向振动特性研究[J]. 振动与冲击, 2014, 33(17): 90-93. Zhu Xiao-hua, Hu Zhi-qiang. Lateral vibration characteristics analysis of a bottom hole assembly based on interaction between bit and rock[J]. Journal of Vibration and Shock, 2014, 33(17): 90-93.
[13] 章杨烈. 钻柱运动学与动力学[M]. 北京: 石油工业出版社, 2001. Zhang Yang-lie. Kinematics and dynamics of drill string [M]. Beijing: Petroleum Industry Press, 2001.
[14] Yang Y X, Zhang S. Adaptive fitting of systematic errors in navigation[J]. Journal of Geodesy, 2005, 79(1-3): 43-49.
[15] Yang Y, Cui X. Adaptively robust filter with multi adaptive factors[J]. Survey Review, 2008, 40(309): 260-270.
[16] Gao S, Zhong Y, Li W. Robust adaptive filtering method for SINS/SAR integrated navigation system[J]. Aerospace Science and Technology, 2011, 15(6): 425-430.
[17] 孙 霄,董景新,顾启泰. 近钻头测斜器最优八位置标定法[J]. 中国惯性技术学报, 2014, 22(1): 5-8. Sun Xiao, Dong Jing-xin, Gu Qi-tai. Optimal 8-position calibration for at-bit inclinometer[J]. Journal of Chinese Inertial Technology, 2014, 22(1): 5-8.
Robust adaptive filtering method for dynamic attitude measurement of steering drilling
GAO Yi1,2, WANG Yue-long1,2, CHENG Wei-bin1,2
(1. Shaanxi Key Laboratory of Measurement and Control Technology for Oil and Gas Wells, Xi’an Shiyou University, Xi’an 710065, China; 2. School of Electronic Engineering, Xi’an Shiyou University, Xi’an 710065, China)
In drilling process, there are serious interferences in the attitude measurement for the steering drilling tool under conditions of near-bit vibration of steering drilling tool, which is due to the bottom drill’s string vibration and would lead to inaccurate attitude measurement. In order to eliminate or weaken these adverse vibration influences on the space attitude measurement and calculate the accurate attitude parameters of drilling tool, a dynamic attitude measurement algorithm with robust adaptive filter is proposed which can effectively eliminate the influence of drilling tool vibration on dynamic attitude measurement and distribute information reasonably by equivalent weight function and adaptive factor. Experimental results and comparison analysis demonstrate that the proposed robust adaptive filtering can eliminate the vibration disturbance signal of the near-bit, the deviation angle can be controlled to about 5.5°, and the tool face angle error is less than 6°. It improves the dynamic measurement accuracy of attitude parameters and solves the problem of uncertainty in dynamic attitude measurement of steering drilling tool.
steering drilling; dynamic measurement; drill string vibration; robust estimation; adaptive filter
TP301.6
:A
2016-04-15;
:2016-07-28
国家自然科学基金(51604226,61174191);陕西省教育厅重点实验室科研计划项目(16JS090);中国石油科技创新基金(2015D-5006-0307);西安石油大学青年科技创新基金项目(2015BS44)
高怡(1978—),女,博士,讲师,从事油气井测控技术、控制理论与控制工程。E-mail: gy@xsyu.edu.cn
1005-6734(2016)04-0437-06
10.13695/j.cnki.12-1222/o3.2016.04.004
