滚珠型单头弧面分度凸轮实体建模及加工仿真研究*

侯加林，冯　爽

(山东农业大学 机械与电子工程学院，山东 泰安 271018)



滚珠型单头弧面分度凸轮实体建模及加工仿真研究*

侯加林，冯爽

(山东农业大学 机械与电子工程学院，山东 泰安 271018)

摘要：目前对单头弧面分度凸轮实体建模有很多研究方法，大多数研究的弧面分度凸轮实体建模过程比较复杂，不仅建模周期比较长，而且实际加工周期也比较长，导致了凸轮设计的效率偏低，不能满足凸轮小批量生产的要求。对此，文章采取了滚珠型单头弧面分度凸轮实体建模的方法，通过Matlab软件选择出优良的滚珠运动规律曲线，编程曲线程序计算出运动规律曲线的对应三维坐标点，保持为文本格式后导入到三维建模软件Pro/E中，从而生成转盘上面的滚珠实际运动轨迹曲线，在运动规律曲线上画出一个圆形，尺寸等于滚珠直径，采用扫略切除命令完成弧面分度凸轮的创建，最后把弧面分度凸轮模型保存为IGES格式，导入到Mastercam软件中进行加工仿真。同时，文中与其它弧面分度凸轮建模及加工仿真进行了对比分析，对比结果显示，文中研究的凸轮不仅建模周期特别短，大约都缩短了67%左右，而且加工仿真时间也特别短，大约缩短了50%左右，因此为弧面分度凸轮的建模与加工仿真提供了参考数据。

关键词：单头；弧面分度凸轮；实体建模；加工仿真

0引言

当前，机械化设备向着高效、高精度和自动化方向的发展，各个企业对机械自动化设备的需求量也不断增加，作为自动化设备核心部件的各种弧面分度凸轮也得到了迅速发展。弧面分度凸轮机构具有很多优良特性，比如：凸轮与其它机构之间的接触相对紧密，传递扭矩比较大；凸轮的整体构造简单灵活，磨损后可以对其进行调整；凸轮所占空间体积相对较小，运动比较平稳。弧面分度凸轮主要应用在包装机械、机械手、专用磨床及加工中心等各种机械领域。

弧面分度凸轮机构其运动类似于蜗轮蜗杆[2]传动，如图1所示。当前对弧面分度凸轮的研究方法有很多，例如：文献[1-2]研究了弧面分度凸轮机构的动态接触。文献[3-4]研究了弧面分度凸轮机构的实体建模及运动仿真。文献[5-6]研究了弧面凸轮三维图形软件的开发。以往对弧面分度凸轮实体建模的研究周期都比较长，导致了凸轮在加工过程中浪费时间，加工效率比较低。因此，本文通过滚珠实际运动轨迹曲线扫略切除分度凸轮毛坯基体的方法，借助于运算软件Matlab和三维建模软件Pro/E，最终完成弧面分度凸轮三维模型的创建，然后将弧面分度凸轮模型保存为IGES格式，导入到Mastercam软件中进行加工仿真。将本文的研究方法与其它建模方法及加工仿真形成了对比，为弧面分度凸轮实体建模及加工仿真的研究提供了参考价值。

图1　弧面分度凸轮机构

1滚珠与凸轮运动过程分析

滚珠运动的轨迹直接决定了弧面分度凸轮建模的精度，必须对滚珠的运动状况进行分析，如图2所示。

图2　滚珠的运动轨迹曲线

每个滚珠运动状况主要分为两个阶段：第一，滚珠要从0°旋转到60°，此过程对应的单头弧面分度凸轮从0°旋转到120°；第二，滚珠要在60°静止一段时间，此过程对应的单头弧面分度凸轮从120°旋转到360°，准备进行下一个滚珠与单头弧面分度凸轮的接触运动。通过滚珠的运动轨迹曲线构造出单头弧面分度凸轮的整个建模和加工仿真流程，如图3所示。

图3单头弧面分度凸轮建模与加工仿真流程图

2滚珠运动规律的选择

在选择滚珠运动规律过程中，同时考虑弧面分度凸轮带动滚珠运动的角位移、角速度、角加速度及角跃度等变化状况，在滚珠的运动过程中，后三个参数值的最大值从理论上要求保持最小，但是滚珠在实际运动过程中，找不到对应的运动规律曲线。常见的滚珠(凸轮从动件)运动规律曲线主要包括以下六种[7-9]：余弦加速度运动规律；正弦加速度运动规律； 3-4-5次多项式运动规律；改进等速度运动规律；改进梯形加速度运动规律；改进正弦加速度运动规律。通过Matlab软件计算出六种运动规律曲线的角速度、角加速度及角跃度的最大值，对比分析得出改进正弦加速度运动规律曲线综合性能相对较好，最终确定改进正弦加速度运动规律曲线作为滚珠的实际运动轨迹。结合Matlab编写相应的程序，得到如图4所示。

图4　转盘与凸轮分度期运动规律曲线

由图4可知，滚珠的角位移、角速度角、加速度及跳跃度在运动过程中确实没有发生突变情况，满足滚珠运动轨迹的要求。

3单头弧面分度凸轮实体建模

3.1弧面分度凸轮实体建模原理

建立弧面分度凸轮实体模型，必须给出相应的运动参数和几何参数，本文不作详细说明了，各个参数值如表1所示。

表1　弧面分度凸轮建模的主要参数值

打开三维造型软件Pro/E，在草图界面中创建2个同心圆，半径分别设置为86mm和 34mm，然后在小圆上画一个矩形，通过修剪命令去掉多余的曲线，点击拉伸命令，拉伸距离为88mm，从而创建出弧面分度凸轮毛坯基体，而文献[5]创建的弧面分度凸轮毛坯基体和本文一样，如图5所示。

图5　弧面分度凸轮毛坯基体

3.2滚珠运动轨迹的三维坐标值计算

本文最终选择改进正弦加速度运动规律曲线作为滚珠的实际运动轨迹，在曲线坐标计算过程中，需要把无量纲时间 (T)、位移(S)、速度(V)和滚珠联系起来考虑。由滚珠的运动轨迹方程式[9-10]可以编写出相应的空间坐标点计算程序，如下所示。

(1)第1个滚珠分度期程序

第1个滚珠分度期开始过程程序：

T=[0:1/240:1];

W=T/8;

R=72;

C=190;

φ1=0;

θ=4*pi/3+2*pi*P/3;

φ=φ1+pi*(pi*P-(sin(4*pi*P))/4)./(3*(4+pi));

X=R*cos(φ).*cos(θ)-C*cos(θ);

Y=-R*cos(φ).*sin(θ)+C*sin(θ);

Z=R*sin(φ);

P=[X;Y;Z];

rot90(P)

第1个滚珠分度期中间过程程序：

T=[0:1/240:1];

W=1/8+6*T/8;

R=72;

C=190;

φ1=0;

θ=4*pi/3+2*pi*P/3;

φ=φ1+pi/(3*(4+pi))*(2+pi*P-9/4*sin((pi+4*pi

*P)/3));

X=R*cos(φ).*cos(θ)-c*cos(θ);

Y=-R*cos(φ).*sin(θ)+c*sin(θ);

Z=R*sin(φ);

P=[X;Y;Z];

rot90(P)

第1个滚珠分度期结束过程程序：

T=[0:1/240:1];

W=T/8+7/8;

R=72;

C=190;

φ1=0;

θ=4*pi/3+2*pi*P/3;

φ=φ1+pi/(3*(4+pi))*(4+pi*P-1/4*sin(4*pi*P))

;

X=R*cos(φ).*cos(θ)-C*cos(θ);

Y=-R*cos(φ).*sin(θ)+C*sin(θ);

Z=R*sin(φ);

P=[X;Y;Z];

rot90(P)

(2)第2个滚珠分度期程序

第2个滚珠程序与第1个滚珠程序相似，将φ1=0改成φ1=- pi/4就可以得到第2个滚珠分度期的整个程序。

(3)第1个滚珠停歇期程序

T=[0:1/480:1];

R=72;

C=190;

θ=4*pi*T/3;

φ1=0;

φ=φ1;

X=R*cos(φ)*cos(θ)-C*cos(θ);

Y=-R*cos(φ)*sin(θ)+C*sin(θ);

Z=R*sin(φ);

Z1=Z*ones(1,481);

P=[X;Y;Z1];

rot90(P)

将上面程序分别输入到Matlab软件中，可以得到滚珠运动轨迹的空间三维坐标点，将三维坐标点保存为文本形式，然后导入到三维软件Pro/E中，如图6所示，而文献[3]创建的滚子曲线结果如图7所示。

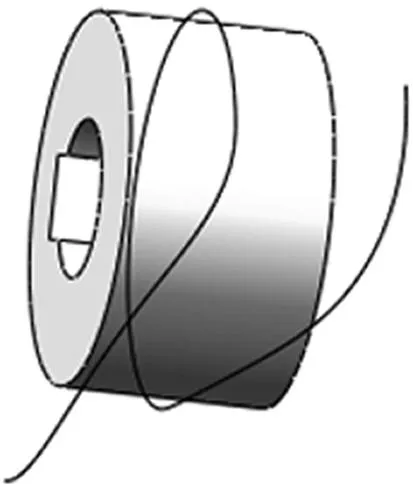
图6　本文滚珠运动曲线

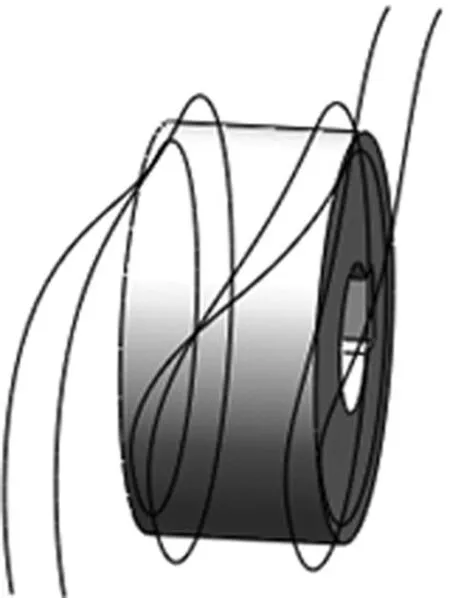
图7　文献[3]滚子运动曲线

3.3单头弧面分度凸轮实体建模

在图6曲线垂直方向上创建一个基准平面，然后在基准平面上画一个圆，直径为40mm，点击扫略切除命令，从而完成单头弧面分度凸轮实体建模，如图8所示，而文献[3]完成的单头弧面分度凸轮实体建模如图9所示。

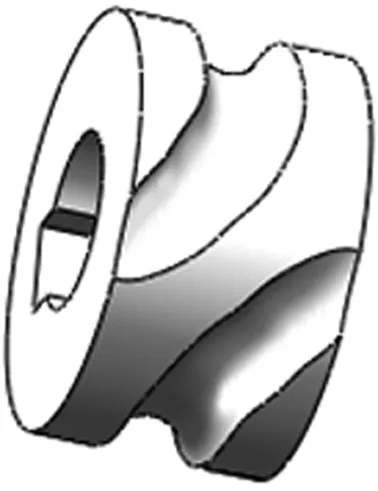
图8　本文凸轮实体模型

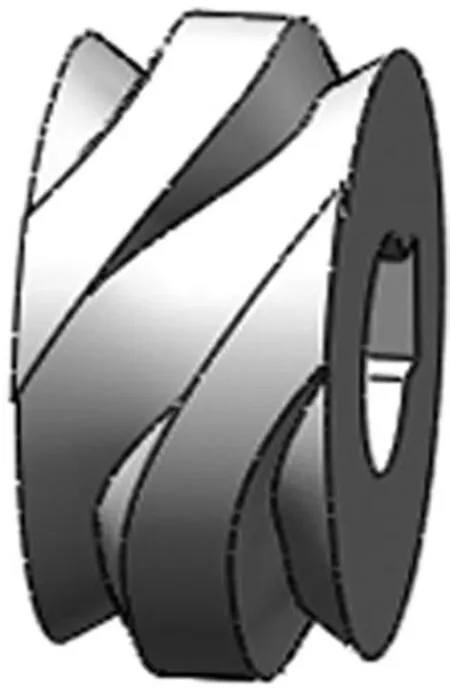
图9　文献[3]凸轮实体模型

通过图6和图7对比可知，本文创建1条运动轨迹曲线，建模周期明显缩短，主要因为本文建模需要第1个滚珠的分度期程序、第1个滚珠的停歇期程序及第2个滚珠的分度期程序，而文献[3]创建2条运动轨迹曲线，建模周期明显增长，需要第1个滚子的分度期程序、第1个滚子的停歇期程序、第2个滚子的分度期程序、第6个滚子的分度期程序及第6个滚子的停歇期程序。另外，分度期主要包括三个阶段，开始、中间级结束，对应计算量也是停歇期的3倍。程序对比结果如表2所示。

表2　单头弧面分度凸轮建模程序计算量

由表2可知，本文建模计算程序量大约缩短了67%，建模速率明显加快快，因此提高了单头弧面分度凸轮的建模效率。

4单头弧面分度凸轮加工仿真

4.1弧面分度凸轮几何建模

数控加工仿真的前提是建立CAD 模型，弧面分度凸轮几何模型是加工仿真的首要环节。曲面建模技术是复杂零件建模主要技术的基础。Mastercam的CAM 模块获得CAD模型的方法途径有以下三种[10]：直接获得、直接造型和数据转换。本文选择的是数据转换，通过三维软件Pro/E中已经建立的弧面分度凸轮实体模型转换为IGES格式文件，导入到MasterCAM软件中，从而得到数控加工仿真的实体模型，如图10所示。文献[3]加工仿真实体模型如图11所示。

图10　本文仿真实体模型

图11　文献[3]仿真实体模型

4.2数控加工仿真参数设置

首先创建机器加工的群组，“机床类型”选择为“铣削”，铣削方式为“默认”，然后对材料进行设置， 在“材料设置”选项卡中，选择沿着“Z轴”方向的“圆柱体”，其余为“默认”，单击“确定”，最后对刀具大小、主轴转速、进给量及切削方式进行设置，如表3所示。参数设置结束后选择“确认”，从而生成数控仿真刀具加工路径，如图12所示。文献[3]数控仿真刀具加工路径如图13所示。

图12　本文刀具加工路径

图13　文献[3]刀具加工路径

序号刀具主轴转速进给量切削方式切削次数1球刀ϕ10mm2000r/min5mm/s双向22球刀ϕ5mm3000r/min0.5mm/s双向1

4.3数控加工仿真验证及NC代码程序生成

选择MasterCAM软件，对单头弧面分度凸轮实体模型生成的刀具路径进行数控加工仿真，观察刀具加工仿真结果。加工仿真主要是验证刀具的运动情况，看看是否存在加工过程中的碰撞、干涉及过切等现象，加工仿真时间大约为1586s，加工仿真结果如图14所示。文献[3]加工仿真时间大约为3072s,仿真结果如图15所示。

图14　本文刀具仿真结果

图15　文献[3]刀具仿真结果

由图14可以看出，本文刀具加工仿真结果正确，然后可以生成NC代码程序，部分程序如下所示。

%

O0000

N100 G21

N102 G0 G17 G40 G49 G80 G90

N104 T244 M6

N106 G0 G90 G54 X-83.318 Y51.256 A-263.885 S1909 M3

N108 G43 H244 Z156.624

N110 X-53.834 Z63.164

5结束语

单头弧面分度凸轮实体建模过程相对其它凸轮机构比较复杂，本文采用Matlab和Pro/E两种软件创建弧面分度凸轮实体模型。该方法比较简单易学，建模周期短，和其它建模方法相比大约缩短了67%左右。同时，加工此凸轮的周期也相对缩短了50%左右，生成的NC代码程序可以直接用于凸轮加工。实体建模和数控加工仿真过程根本不要掌握复杂的编程语言，节约了凸轮实体建模和数控加工的时间。因此，该建模方法及加工仿真为单头弧面分度凸轮进一步的研究提供了一定的参考意义。

[参考文献]

[1] Jao-Hwa Kuang , Chao-Ming Hsu , Chin-Che Hu.Dynamic behavior of globoidal cam systems with torque compensation mechanisms[J].Mechanism and Machine Theory,2010,45(8):1201-1214.

[2] 张三，张国庆.弧面分度凸轮机构的动态接触分析[J].机械设计，2014,31(2):35-39.

[3] 张文光，王大镇，弓清忠，等.单头弧面分度凸轮实体建模新方法及运动仿真[J].组合机床与自动化加工技术，2014(2):45-48.

[4] 张文光,王大镇,弓清忠.采用SolidWorks的弧面分度凸轮三维造型设计与运动仿真分析[J].现代制造工程, 2014 (10):60-94.

[5] Shuting Ji , Jing Zhao, Yueming Zhang.An application of geodesics to the calculation of the rib-thickness of globoidal cam mechanisms[J].Mechanism and Machine Theory,2015,87(10): 163-176.

[6] 周明贵,曹西京,曹巨江,等.弧面凸轮三维图形软件的开发[J].工程图学学报，2005(4):151-154.

[7] 黄薇,葛正浩,刘韦华.三种建模方法对弧面分度凸轮模型的影响研究[J].机械传动,2012,36(11):68 -69.

[8] 刘建慧,邹慧君.加工中心自动换刀装置类型综述及设计特点[J].机械设计与研究,2001,17(3): 49 -52.

[9] 李蕾,冯显英,张紫平,等.钢球滚子弧面分度凸轮机构的三维建模及运动仿真[J].机床与液压,2010,38(21):102 -105.

[10] 徐燕申,张学玲.机床结构模块化设计中CAD模型与有限元模型的数据交换[J].组合机床与自动化加工技术,2003(10):30-32.

(编辑赵蓉)

申请优先审稿须知

为振兴我国机械装备制造业，弘扬民族科学文化精神，提升期刊质量，本刊从即日起，凡是符合本刊报道范围且同时受到“国家863计划资助项目”、“国家自然科学基金资助项目”、“国家重点科技攻关资助项目”等国家级基金资助项目的原创论文，可申请优先审稿，一经录用，优先发表，欢迎业内人事、专家、学者踊跃投稿(来稿注明：“优先审稿”字样)。

注：1.本刊正常审稿时间一般为一个月，优先审稿时间为15-20天;

2.本刊正常发表文章周期为采用后7-10个月，优先发表文章周期为7-9个月。

——本刊编辑部

Research on Modeling and Processing Simulation of Ball Type Single Head of Globoidal Indexing Cam Entity

HOU Jia-lin，FENG Shuang

(College of Mechanical and Electronic Engineering, Shandong Agricultural University, Tai’an Shandong 271018,China)

Abstract：At present, there are many research methods of single head of globoidal indexing cam modeling, entity modeling process of globoidal indexing cam is most research is more complex, not only the modeling cycle is long, but the actual processing cycle is relatively long, may lead to lower efficiency of cam design, can not meet the requirements of the cam and small batch production. Therefore, this paper adopts the method of ball type single head of globoidal indexing cam modeling, through the Matlab software to select excellent curve ball movement rules, programming curve program calculates the motion curve of the corresponding 3D coordinates of points, to keep the text format and imported into 3D modeling software Pro/E, to generate the actual motion trajectory curve ball turntable the above, draw a circle in the motion curve, size is equal to the diameter of the ball bearing, using sweep command to create a complete resection of the globoidal indexing cam, and finally the globoidal indexing cam model is saved as IGES format, and imported into Mastercam software for processing simulation. At the same time, this paper and other globoidal indexing cam modeling and Simulation of machining were analyzed. The comparison results show that this research not only modeling cam cycle is short, about all reduce by about 67%, and the time of machining simulation is particularly short, approximately shortened by about 50%, thus provides reference data for modeling and Simulation of machining globoidal indexing cam.

Key words：single head; globoidal indexing cam; solid modeling; process simulation

中图分类号：TH166；TG659

文献标识码：A

作者简介：侯加林(1963—)，男，山东泰安人，山东农业大学教授，博士生导师，研究方向为智能检测与自动化仪表，(E-mail)hjl3052101311@126.com。

*基金项目：山东省自然科学基金资助项目(ZR2010EQ020)

收稿日期：2015-04-13

文章编号：1001-2265(2016)02-0129-05

DOI:10.13462/j.cnki.mmtamt.2016.02.037