椭圆曲线回转类零件NURBS插补算法研究*

翟静涛，赵国勇，庄丙远，岳　磊

(山东理工大学 机械工程学院，山东 淄博　255049)



椭圆曲线回转类零件NURBS插补算法研究*

翟静涛，赵国勇，庄丙远，岳磊

(山东理工大学 机械工程学院，山东 淄博255049)

摘要：针对激光熔覆加工中椭圆曲线回转类零件，提出了利用NURBS曲线直接对椭圆曲线零件拟合、插补的算法。在NURBS曲线建模的理论基础上，利用一阶泰勒展开式对插补点进行迭代运算，结合可控弓高误差插补理论，对刀轨曲线进给速度进行了规划。插补加工实例说明，对于椭圆曲线回转类零件，所提出方法满足加工精度要求，达到了预期的加工目标。

关键词：激光熔覆加工；椭圆曲线；NURBS；弓高误差

0引言

激光熔覆技术是伴随激光加工兴起的一项新型工艺，因在材料表面改性中的突出优点而获得了国内外大多学者的广泛关注和研究[1-2]，在再制造和快速成型领域被迅速推广应用。

对于激光熔覆加工中椭圆曲线回转类零件，主要采用直线和圆弧逼近，理论和实验证明采用直线段逼近复杂曲线并使用线性插补加工，对精度和速度的要求是一对矛盾[3-6]。鉴于以上两方法的不足，以及NURBS插补在复杂几何造型方面的独特优势，提出了用NURBS曲线直接拟合、插补椭圆曲线回转类零件的算法。在X-Z坐标平面内进行NURBS曲线建模，通过弓高误差控制进给速度，并对具体零件进行了插补加工验证。

1NURBS曲线的简述

1.1NURBS曲线的定义

对于任意一条k次NURBS(Non-Uniform Rational)曲线都可以表示为一分段矢值多项式函数[7-9]：

(1)

其中，ωi(i=0,1,...,n)称为权值,与控制顶点di(i=0,1,...,n)相联系，ω0,ωn>0,其余ωi≥0,Ni,k(u)是由节点矢量U=(u0,u1,...,un+k+1)根据Cox-de Boor递推公式决定的B样条基函数，表达形式如下：

(2)

其中，k表示次数，i表示序号。

1.2二次NURBS的矩阵表达形式

鉴于本文采用二次NURBS曲线对椭圆拟合、插补，本部分研究了二次NURBS曲线的矩阵表达算法。由式(1)得二次NURBS曲线的表达式，即当k=2时，

(3)

其中，Ni,2(u)为二次有理B样条基函数，为了描述简洁化，引入符号Δ，并且满足：

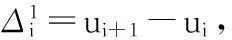
同时，指定 U=[1uu2]，0≤u≤1；

Wi=[ωiωi+1ωi+2]T；

Di=[diωidi+1ωi+1di+2ωi+2]T

根据Cox-deBoor递推公式得到二次NURBS曲线的矩阵表达式为：

(4)

1.3二次NURBS曲线对椭圆曲线的拟合

二次NURBS曲线跟同次B样条曲线一样，具有端点插值性，即在起点和终点分别与各自控制顶点重合，且在端点与特征多边形边相切[10]。

采用二次NURBS对椭圆曲线进行拟合，包括以下步骤：

步骤1：要根据具体的椭圆曲线方程来设置控制顶点di和权因子ωi；

步骤2：按照参数u从0～1循环，依次代入公式(4)进行运算，可以得到曲线上的各个对应点pi(u)；

步骤3：将生成的各个对应点依次相连，从而得到所要拟合的椭圆曲线。

2NURBS曲线实时插补

2.1NURBS曲线实时插补

NURBS曲线实时插补流程如图1所示。

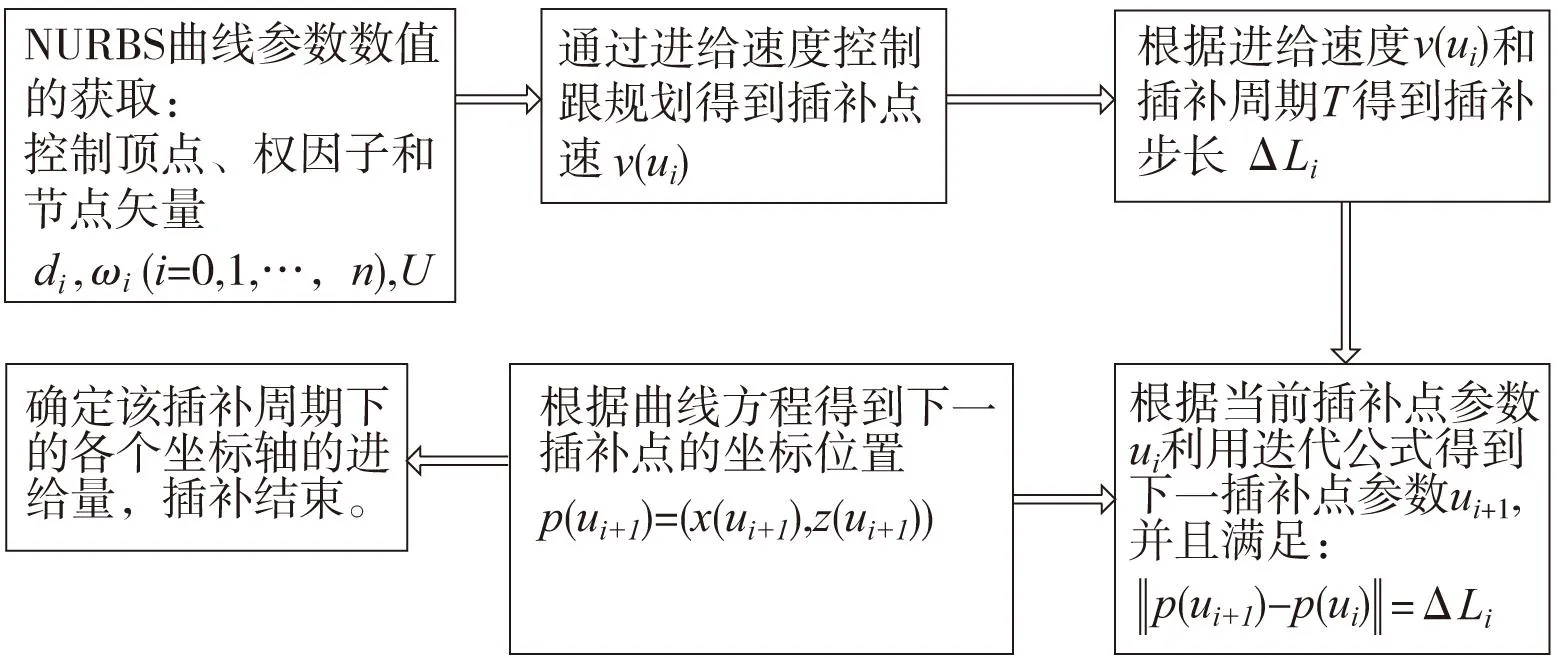
图1　NURBS曲线实时插补流程

样条插补中实时插补的核心是插补参数的计算，对于NURBS插补，只要根据已知参数值ui求得下一点的参数值ui+1，代入式(1)便能得到下一插补点p(ui+1)的坐标位置。由于通过二次NURBS曲线进行插补，本文采用一阶泰勒展开式作为参数值之间的迭代公式。

将参数u对时间参数t求导并进行一阶泰勒展开得：

(5)

其中,T=ti+1-ti，o(t2)为t2的高阶无穷小量；

又因为

(6)

设p(u)为所要插补的二维NURBS曲线，其矢函数表达式为p(u)=(x(u),z(u))，则

(7)

综合式(5)、(6)、(7)得一阶泰勒展开式为：

(8)

2.2控制弓高误差自动调节速度算法

在NURBS的实时插补中，为保证弓高误差限制在一定范围内，必须随着曲线曲率的变化来调节进给速度。通常采用圆弧近似的方法求出弓高误差、进给速度以及曲率之间的关系，如图2。

图2　圆弧近似求解弓高误差示例图

由图2可以得到以下几何关系：

(9)

(10)

Li=v(ui)Ts

(11)

(12)

由公式(9)～(11)，得到:

(13)

设定编程速度为F，允许最大轮廓误差为Ermax，则进给速度的调节算法为：

v(ui)=

(14)

3椭圆曲线回转类零件插补实例

激光熔覆加工中某椭圆曲线回转类零件，如图3所示。通过分析所要插补的椭圆曲线部分，用NURBS曲线拟合，如图4所示。设控制顶点数共6个，依次分别为点A、B、D、F、H、I，其中，通过设置曲线的结点C、E、G, 将所要拟合的椭圆曲线总共分为4段。

具体参数包括控制顶点，节点矢量，权因子依次分别设置如下：

di:[(-12,12)(0, 18.75)(20, 7.231)(20,-7.231)

(0,-18.75)(-12,-12)]；

U:[0,0,0,0.2871,0.5000,0.7129,1,1,1]；

ωi: [1,0.8,1,1,0.8,1]。

设进给速度F=12m/min,允许最大轮廓误差Ermax=1μm,插补周期Ts=1ms。插补结果如图5～图7所示。

通过对照图4、图5，拟合曲线跟插补曲线整体趋近于重合，验证了NURBS曲线对非圆曲线插补的可行性。

如图6，通过分析轮廓误差曲线图可以看出在整个插补过程中，轮廓误差曲线整体以参数值u=0.5为对称轴呈现左右两边对称，完全符合了被插补椭圆曲线本身轴对称的特性，且在节点参数u=0.45附近对称出现最大误差数值。

通过对仿真结果的分析可以得到在整个插补过程中，轮廓误差始终被限制在最大弓高误差Ermax=1μm的约束条件内，完全满足加工要求，达到了预期的目标。

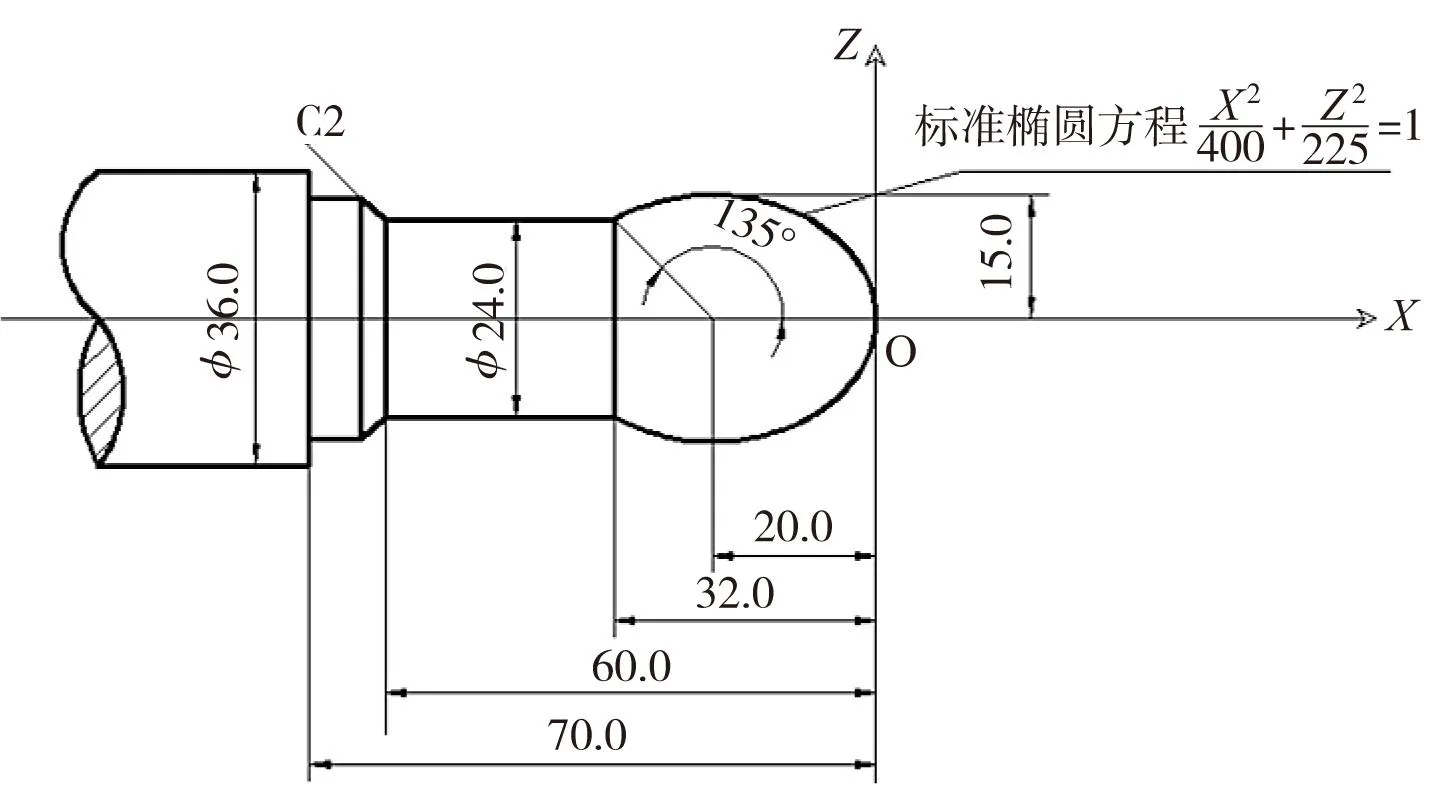
图3　激光熔覆加工中某椭圆曲线回转类零件

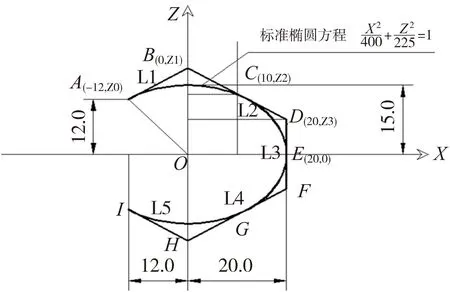
图4　用NURBS拟合椭圆曲线零件过程

图5　NURBS曲线描述拟合椭圆曲线结果

图6　椭圆曲线轮廓NURBS插补结果

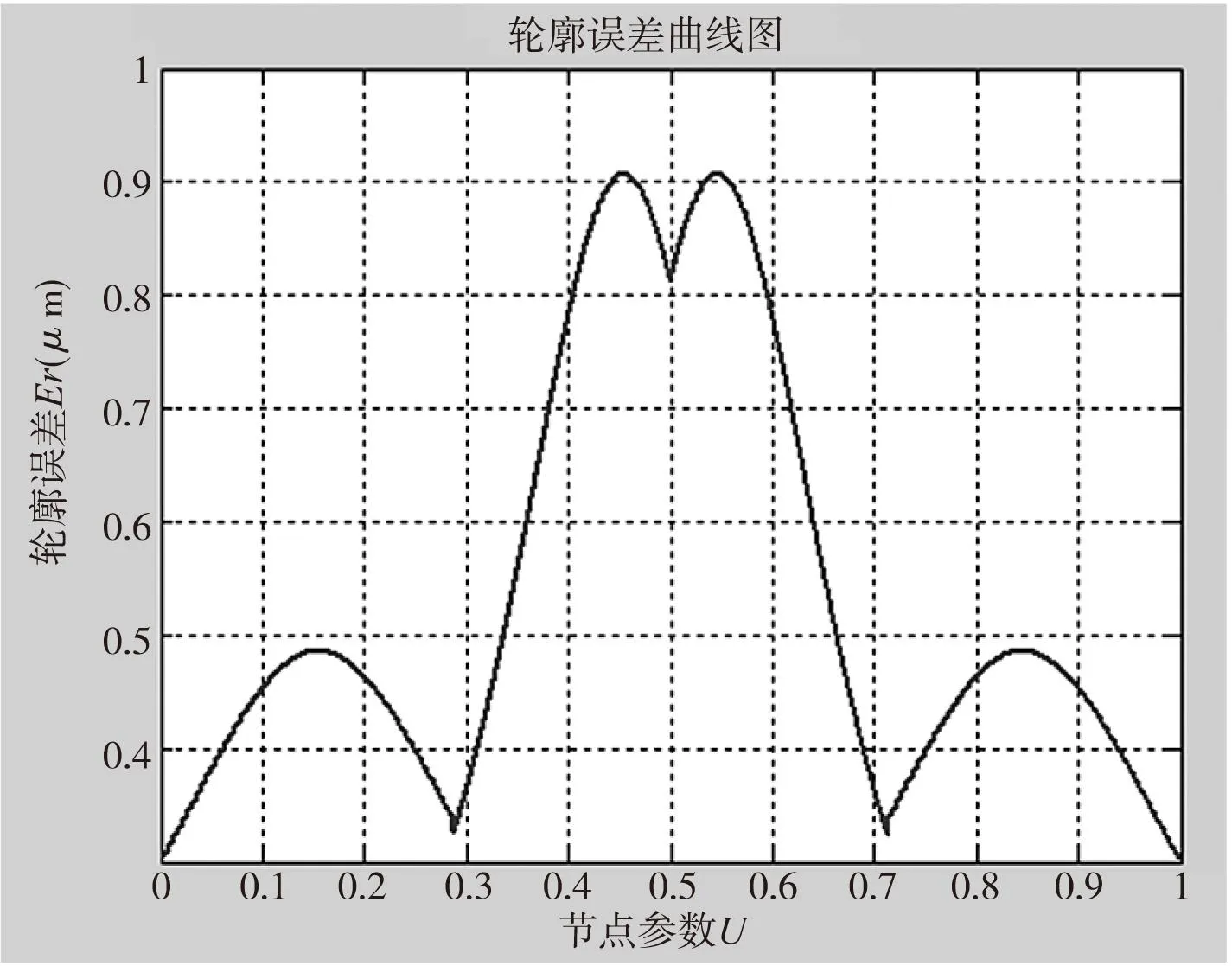
图7　NURBS插补轮廓误差曲线图

4结束语

针对激光熔覆加工中椭圆曲线回转类零件的插补研究，提出了利用NURBS曲线对椭圆曲线拟合、插补算法，利用控制弓高误差自动调节进给速度，对进给速度进行控制和规划，满足了轮廓误差要求，拟合、插补实例验证了该方法的合理性。预计可以进一步提高该类零件激光熔覆加工的效率和精度。

[参考文献]

[1] 张坚,吴文妮,赵龙志.激光熔覆研究现状及发展趋势[J].热加工工艺,2013,42(6):131-134,139.

[2] 陈光霞.激光快速成型矩形分区扫描算法的实现[J]. 组合机床与自动化加工技术,2010(5):107-109.

[3] 黄国辉.基于DSP的NURBS曲线高速高精度实时插补算法的研究与实现[D].广州:广东工业大学,2013.

[4] 王允森,盖荣丽,孙一兰,等.面向高质量加工的NURBS曲线插补算法[J].计算机辅助设计与图形学学报,2013,25(10):1549-1556.

[5] 林志炜.高速数控系统中NURBS曲线自适应插补的实现及其加减速控制策略研究[D].合肥:中国科学技术大学,2014.

[6] 周胜德,梁宏斌,乔宇. 基于NURBS曲线插补的五段S曲线加减速控制方法研究[J]. 组合机床与自动化加工技术,2011(4):37-41,46.

[7] Lei W T, Sung M P. NURBS-based fast geometric error composition for CNC machine tools [J]. International Journal of Machine Tools & Manufacture, 2008, 48(3).

[8] Yeh S S, Hsu P L. The speed-controlled interpolator for machining parametric curves [J]. Computer-Aided Design, 1993, 31 (5):349-357.

[9] Zhang Deli, Zhou Laishui. Intelligent NURBS Interporlator Based on the Adaptive Freedrate Control [J].Chinese Journal of Aeronautics, 2007, 5:469-474.

[10] 朱虹.基于NURBS曲线拟合的复杂回转体零件加工技术研究[J].机械设计与制造2013(4):214-216.

(编辑赵蓉)

Research on NURBS Interpolation Algorithm for Rotational Parts with Elliptic Curve

ZHAI Jing-tao, ZHAO Guo-yong, ZHUANG Bing-yuan, YUE Lei

(School of Mechanical Engineering, Shandong University of Technology, Zibo Shandong 255049,China)

Abstract：For the rotational parts with elliptic curves in laser cladding process, an interpolation algorithm based on NURBS is proposed to make use of the curve itself to approximate and interpolator the parts with elliptic curve directly. On the basis of the theory about the curve modeling, an iterative calculation which is composed by the first order Taylor’s expansion is developed for interpolation. Based on the algorithm of the controlled chord error interpolator, the feederate can be under control. As the result of an example in interpolation process, the algorithm is proved effective to meet the need of machining accuracy for the rotational parts with elliptic curves, and achieve the processing target expected.

Key words：laser cladding process; elliptic curve; NURBS; chord error

中图分类号：TH161;TG659

文献标识码：A

作者简介：翟静涛(1989—)，男，山东淄博人，山东理工大学硕士研究生，研究方向为数控技术与装备；通讯作者：赵国勇(1976—)，男，山东淄博人，山东理工大学教授，硕导，博士，研究方向为机械制造自动化技术，(E-mail)zgy709@126.com。

*基金项目：国家自然科学基金项目"五轴联动数控机床轮廓误差耦合控制理论与方法研究"(51105236)

收稿日期：2015-04-25;修回日期：2015-05-19

文章编号：1001-2265(2016)02-0112-03

DOI:10.13462/j.cnki.mmtamt.2016.02.032