基于变增益MRAI转动惯量辨识及控制参数优化*

董烈超，周凤星，卢少武

(武汉科技大学 信息科学与工程学院，武汉　430081)



基于变增益MRAI转动惯量辨识及控制参数优化*

董烈超，周凤星，卢少武

(武汉科技大学 信息科学与工程学院，武汉430081)

摘要：为了使交流伺服系统在不同负载情况下运行时，保持良好动、静态特性，需实时辨识系统转动惯量并及时调整控制器控制参数。提出一种变增益模型参考自适应辨识法(MRAI)对系统的转动惯量进行精确辨识，并根据辨识结果结合速度控制器的数学模型，采用遗传算法对速度控制器的PI控制参数进行优化的方法，实现对交流伺服系统控制参数的整定优化。仿真结果表明，变增益模型参考自适应辨识法辨识精度高、收敛速度快，结合遗传算法对速度控制器参数进行优化，有效提高了交流伺服系统的动态特性，增强了系统的稳定性。

关键词：交流伺服系统；模型参考自适应；转动惯量；遗传算法

0引言

数控机床、智能机器人等领域都对永磁同步电机交流伺服系统的速度动态性能和控制精度有很高的要求。当负载转动惯量发生变化时，会对整个交流伺服系统的机械特性造成明显影响。因此，准确、快速地辨识出交流伺服系统的转动惯量值，并且根据转动惯量辨识结果对相应的速度控制器控制参数进行整定优化[1-3]，是提高交流伺服系统速度控制器动态性能的有效途径。

目前，众多学者在交流伺服系统转动惯量辨识和控制参数优化方面做了大量研究。文献[4]提出了含遗忘因子递推平方根算法进行转动惯量在线辨识，该方法辨识结果准确，但该方法运行时占用较多的处理器内存，运算速度偏慢。文献[5-6]提出了模型参考自适应辨识法应用在伺服系统转动惯量辨识中，该方法具有辨识精度高、辨识过程收敛速度快的优点。文献[7-8]提出了遗传算法应用于伺服系统控制参数整定优化，该算法结构开放且易于与实际问题相结合，且具有并行计算、全局收敛、编码操作、运算速度快等特点，在交流伺服系统速度控制器控制参数优化上具有良好的可行性和准确性。

本文采用变增益模型参考自适应辨识法对交流伺服系统转动惯量进行辨识，根据辨识得到的系统转动惯量值，采用遗传算法对当前工作环境的交流伺服系统速度PI控制器控制参数进行优化。在Matlab环境下进行仿真，实验结果较为理想，表明该方法具有良好的可行性和稳定性，且有效提高了交流伺服系统的鲁棒性。

1永磁同步电机的数学模型

永磁同步电机的机械运动方程为：

(1)

(2)

式中ωr为永磁同步电机机械角速度，Te为电磁转矩，Tl为负载转矩，B为摩擦系数，J为转子转动惯量,pn为极对数，ψf为永磁体磁通，iq为q轴电流。

2基于变增益参考模型自适应辨识法

基于模型参考自适应的辨识方法是将实际系统作为参考模型，并建立含有未知参数的可调模型。两模型具有相同物理意义的输入与输出量，比较两个模型的输出，通过某种自适应规律调整可调模型的参数，最终实现可调模型输出跟随参考模型输出。在这个过程中，可调模型的输出尽可能地接近实际输出，可调模型的未知参数逐渐接近实际情况。当可调模型的输出和参考模型的输出偏差不再改善时，则可调模型的未知参数被作为待辨识参数的估计值，即辨识结果。

忽略摩擦阻力，将永磁同步电机的机械运动方程(1)离散化：设采样时间为T，则离散方程如下[9]：

(3)

(4)

由于采样时间较短，电机所带转矩负载的变化周期远远大于惯量辨识控制周期，可以认为在k-1,k-2时刻的负载转矩不变，即

Tl(k-1)=Tl(k-2)

(5)

由式(3)减式(4)，可得式(6)：

ωr(k)=2ωr(k-1)-ωr(k-2)+b(k)ΔTe(k-1)

(6)

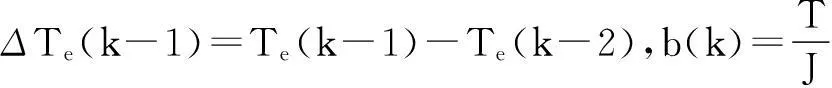
将上式作为参考模型，可得可调模型方程为：

ωg(k)=2ωr(k-1)-ωr(k-2)+bg(k)ΔTe(k-1)

(7)

式中，ωg为估计速度，bg为估计变量。参考模型和可调模型的输出误差为：

ε(k)=ωr(k)-ωg(k)

(8)

Popov超稳定性理论有如下特点：利用函数来判断系统的全局和局部渐进的稳定性，无需求解系统的微分方程，可以准确得到系统的自适应律[10]。由Popov超稳定性理论设计的转动惯量的自适应律为：

(9)

式中β为自适应增益因子。β越大，辨识过程收敛速度越快但辨识结果波动较大，β越小辨识精度越高但收敛时间越长。为了保证辨识算法具有较高的辨识精度，同时使辨识过程具有快速收敛性，本文采用变增益模型参考自适应辨识法：即当交流伺服系统转动惯量发生变化时，增益因子β跟随变化。当系统转动惯量发生突变时，β值迅速变大，满足快速跟踪系统转动惯量变化的要求，当跟踪到到真实值后，再逐渐减小β值，保证辨识结果的精确性。变增益因子算子如下式：

(10)

式中：λ为调整系数，λ越小β衰减速度越快。

3基于遗传算法速度PI控制参数整定

3.1速度PI控制器数学模型

在交流伺服系统中，电流环的时间常数很小，远小于速度环时间常数，因此可将电流环近似为一阶小惯性环节。电流控制器的闭环传递函数为：

(11)

τi为电流环时间常数，速度环等效原理如图1所示。

图1　速度环等效原理

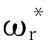
(12)

3.2基于遗传算法的PI控制参数优化

以速度环为被控对象，根据辨识的实时转动惯量值，采用遗传算法对当前系统的速度环PI控制参数kp和ki进行寻优[11]。由于实数编码具有算法精度高、占用存储空间小的特点，采用实数编码方式对参数kp和ki进行编码。

(1)初始种群。以原系统参数kp和ki为一个个体，并在原参数为中心，在参数范围内随机产生N-1个均匀分布的个体，构成N个个体的初始种群。

(2)适应度函数。本文PI参数寻优的最小目标函数采用误差绝对值时间积分，为了防止控制能量过大，加人控制输入的平方项，最小目标函数表达式如下：

(13)

式中，e(t)为系统误差，u(t)为控制器输出，tu为上升时间，w1,w2,w3为权值。

(3)控制参数选择。本文使用的样本个数为30，交叉概率Pc为0.9，变异概率Pm为0.033，终止进化代数为100。

根据适应度的大小，通过复制、交叉、变异等操作，对经过实数编码的初始PI参数进行评价与优化，直到达到终止条件，所获得的参数就是符合控制要求的一组最优PI控制参数。

4仿真试验与结果分析

在Matlab平台的Simulink进行仿真。为了验证本文提出变增益因子模型参考自适应辨识法相比传统方法具有辨识速度快、辨识精度高的优点，和固定增益模型参考自适应算法进行对比实验。根据固定增益模型参考自适应辨识法的特点，需选取较大和较小两组增益因子进行测试，较小的β值设定为0.8，较大的β值设定为100。而变增益模型参考自适应的调整系数λ设定为0.8。设定PMSM仿真模型转动惯量为0.0004kg·m2，为了测试两种模型参考自适应算法的辨识效果，在t=0.3s时，使系统转动惯量阶跃至J1=2J。固定增益模型参考自适应算法中增益因子为0.8的辨识结果如图2所示，增益因子为100的辨识结果如图3所示，变增益模型参考自适应算法的辨识结果如图4所示。

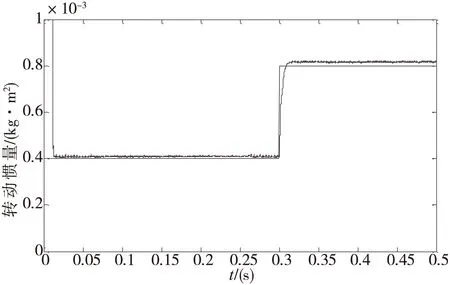
图2　增益因子β=0.8时转动惯量辨识结果

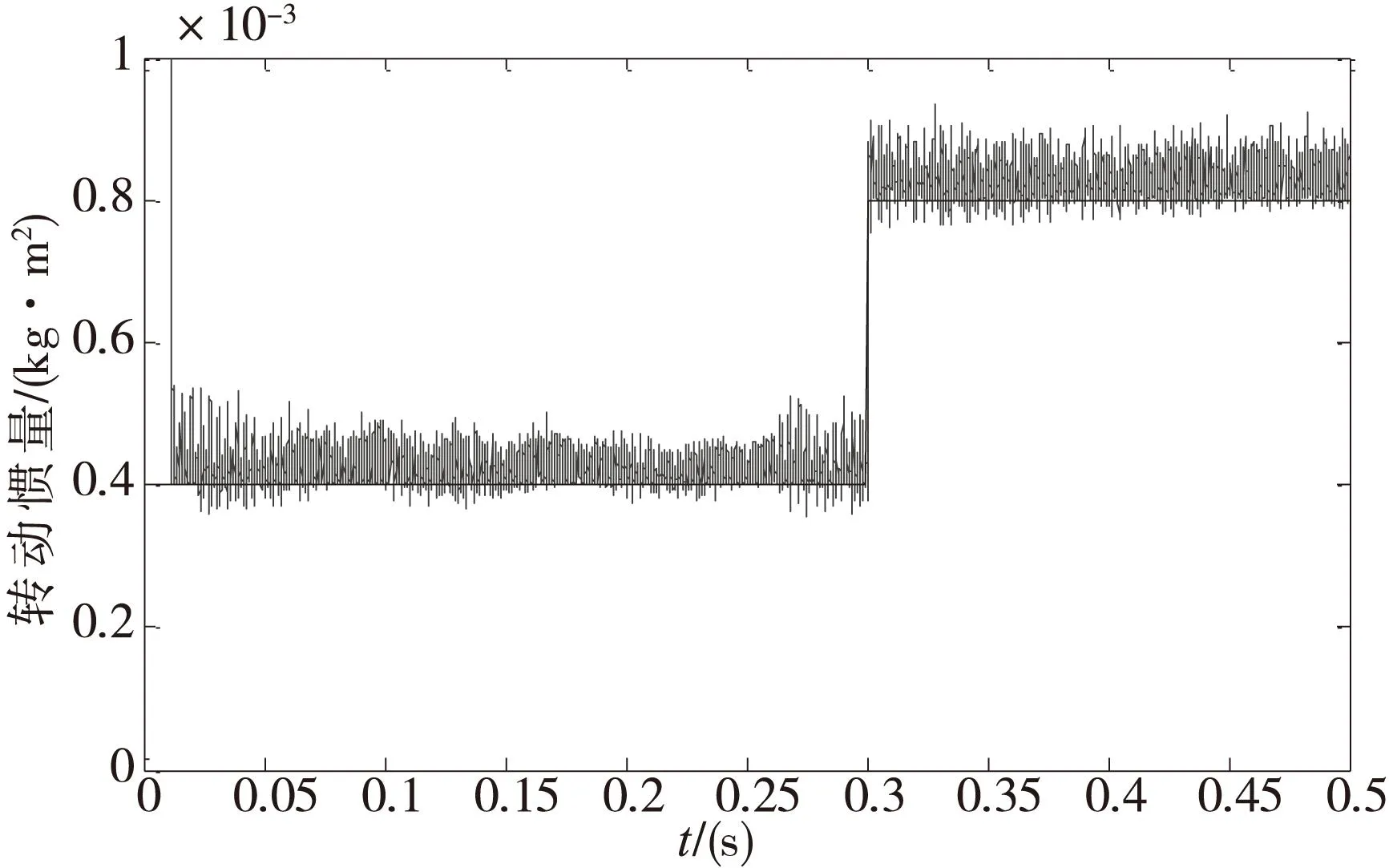
图3　增益因子β=100时转动惯量辨识结果

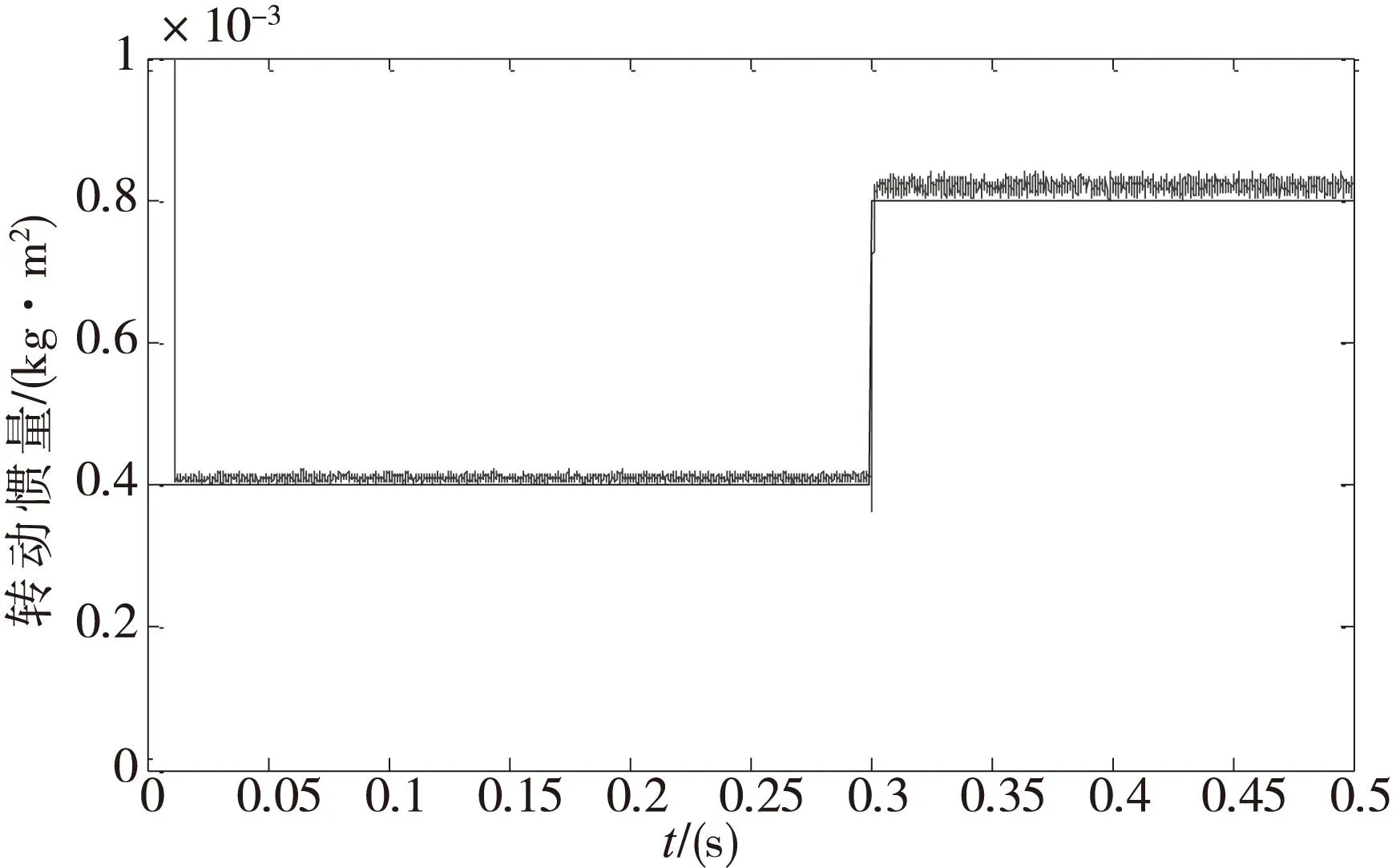
图4　变增益算法转动惯量辨识结果

观察实验结果，当增益因子β=0.8时，辨识结果收敛于真实值，在0.3s时刻，当转动惯量阶跃至2J时，辨识结果为8.15×10-4kg·m2，辨识误差为1.9%，稳定收敛于0.0008kg·m2，但是收敛时间相对较长；当增益因子β=100时，辨识结果波动明显，且误差比较大，但在转动惯量发生阶跃时，能快速跟随实际转动惯量变化值，跟踪速度较快。采用变增益模型参考自适应算法，辨识结果稳定收敛于真实值，且当转动惯量发送阶跃时，辨识值能较快的跟随实际值，辨识结果为8.21×102kg·m2，辨识误差为2.6%，辨识结果准确稳定。

实验验证，相比固定增益模型参考自适应辨识法，变增益模型参考自适应辨识法具有辨识稳定精准，收敛速度快的优点。

将转动惯量辨识值带人速度环传递函数中，采用遗传算法对交流伺服系统速度环PI控制参数进行优化，将优化后的PI控制参数更新到交流伺服系统控制器中。

设定转速为1000r/min，实际转速如图所示，在PI控制参数为优化前，交流伺服系统的速度波形如图5所示，交流伺服系统转速超调量较大，经过100ms左右，转速稳定在设定转速值。通过遗传算法优化后，将获得最优PI控制参数带人控制器，交流伺服系统的转速波形如图6所示，系统转速超调量较小，且在70ms左右，系统转速稳定在设定转速值。

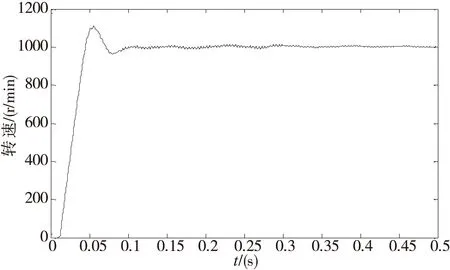
图5　初始PI控制参数时伺服系统转速波形

图6　PI控制参数优化后伺服系统转速波形

实验结果验证，采用变增益模型参考自适应辨识法能快速准确的辨识出当前交流伺服系统的转动惯量，结合遗传算法对速度环PI控制参数进行优化，能有效抑制交流伺服系统的转速超调，提高系统的动态响应速度。

5结束语

本文采用变增益模型参考自适应辨识法对交流伺服系统转动惯量进行辨识，辨识过程收敛速度快、辨识结果精确，根据系统实际转动惯量辨识值和交流伺服系统的数学模型，结合遗传算法对交流伺服系统控制器的控制参数进行优化，获取当前运行环境下的最优控制参数，从而极大的提高了交流伺服系统的动态特性，增强了系统的鲁棒性。

[参考文献]

[1] 郭宇婕, 黄立培, 邱阳. 交流伺服系统的转动惯量辨识及调节器参数自整定[J]. 清华大学学报, 2002, 42(9): 1180-1183.

[2] 赵希梅, 郭庆鼎.PMSM伺服系统的转动惯量辨识和控制器参数优化[J]. 组合机床与自动化加工技术,2009(7): 75-77.

[3] 杨明, 张扬, 曹何金生,等. 交流伺服系统控制器参数自整定及优化[J]. 电机与控制学报, 2010, 14(12): 29-34.

[4] 杨明, 刘子剑, 徐殿国. 基于遗忘因子递推平方根的在线转动惯量辨识[J]. 微电机, 2014, 47(10): 38-41.

[5] 卢少武, 唐小琦, 宋宝. 伺服系统转动惯量辨识及其应用[J]. 微电机，2011, 44(10): 41-43.

[6] 滕福林, 李宏胜, 张建华. 基于朗道离散时间递推算法的转动惯量辨识研究[J]. 微电机, 2012, 45(1): 16-19.

[7] 牛芗洁, 王玉洁, 唐剑. 基于遗传算法的PID控制器参数优化研究[J]. 计算机仿真，2010, 27(11): 180-182.

[8] 李浩, 蒋雪峰, 黄文新. 基于遗传算法的永磁同步电动机PI参数自整定[J]. 微特电机, 2015, 43(1):58-61.

[9] 桑妤. 永磁同步电机转动惯量辨识算法研究[D]. 武汉:华中科技大学, 2013.

[10] 叶汉民, 时晓霞. 基于波波夫超稳定性在永磁同步电机控制系统中的应用[J]. 化工自动化及仪表, 2010, 37(4): 89-92.

[11] 刘金琨. 先进PID控制MATLAB仿真[M]. 北京: 电子工业出版社, 2004.

(编辑赵蓉)

Inertia Identification Based on Variable Gain Model Reference Adaptive Identification and Optimization of Control Parameters

DONG Lie-chao, ZHOU Feng-xing, LU Shao-wu

(College of Information Science and Engineering, Wuhan University of Science and Technology, Wuhan 430081,China)

Abstract：To obtain good dynamic and static performances in the AC servo system, when the motor load rotational inertia changes, the controller parameters are required adjusting based on the load rotational inertia. The method to precise identification the rotational inertia based on the variable gain model reference adaptive identification(MRAI), the result and the mathematical model of speed controller are used to optimize the PI control parameters based on genetic algorithm is developed, thus the optimization of the controller parameters of AC servo system is implemented. The simulation results indicate that the variable gain MRAI has high identification precise, and optimizes the speed controller parameters combined with genetic algorithm, effectively improve the dynamic performance and enhance the stability of the servo system.

Key words：AC servo system; model reference adaptive; rotational inertia; genetic algorithm

中图分类号：TH166;TG506

文献标识码：A

作者简介：董烈超(1990—)，男，湖北荆门人，武汉科技大学硕士研究生，研究方向为伺服控制和嵌入式，(E-mail)15002705683@163.com。

*基金项目：国家自然科学基金项目(61174106)；国家自然科学基金项目(51405349)；中国博士后科学基金项目(2014M552091)

收稿日期：2015-04-01

文章编号：1001-2265(2016)02-0088-03

DOI:10.13462/j.cnki.mmtamt.2016.02.025