模糊赋范空间中的有界性与算子的紧性

2020-06-21李欣欣吴健荣

苏州科技大学学报(自然科学版) 2020年2期

李欣欣，吴健荣

（苏州科技大学数理学院，江苏苏州215009）

模糊赋范空间是经典赋范空间的推广。1984年，Katsaras[1]首先引入了线性空间中模糊范数的定义。1992年，Felbin[2]通过引入模糊实数定义了与Kaleva 型模糊度量对应的模糊范数。1994年，Cheng 和Mordeson[3]在线性空间中引入了KM-型模糊范数。此后不久，Bag 和Samanta[4]引入了类似的模糊范数的定义，并给出了有限维模糊赋范空间中模糊有界子集的表达形式。在此基础上，Bag 和Samanta[4-6]进一步研究了算子的模糊连续、模糊强连续、模糊弱连续、序列模糊连续，以及算子的模糊有界、模糊强有界、模糊弱有界、一致模糊有界等问题。2007年，Fatemeh Lael 和Kourosh Nourouzi[7]在Bag 和Samanta 工作的基础上，定义了模糊紧算子，得到了模糊紧算子的一些基本性质。相关学者也在该领域内做了一定的研究[8-13]。

笔者对文献[4]中的模糊赋范空间作了适当的修改，给出了该空间中模糊有界集、模糊强有界集、模糊弱有界集的定义，并得到了三者的有效刻画。同时，定义了此类模糊赋范空间的S－模糊紧算子，得到了S－模糊紧算子的一些基本性质，进一步丰富了模糊赋范空间中的紧性理论。文章主要分为四个部分：第一部分为预备知识；第二部分为模糊赋范空间中子集有界性及其刻画；第三部分为模糊赋范空间中S－模糊紧算子的定义及基本定理；第四部分为结语。

1 预备知识

该节主要介绍文章所需要的相关定义。

定义1[14]称二元算子*：[0，1]×[0，1]→[0，1]是连续的t-算子，如果*满足：对任意的a，b，c，d∈[0，1]，

（1）满足交换律a*b＝b*a；

（2）满足结合律（a*b）*c＝a*（b*c）；

（3）当a≤c且b≤d时，a*b≤c*d；

（4）a*1=a；

（5）*是连续的。

下面是常用的模糊t-算子的例子，对任意的a，b∈[0，1]，

（i）aΔ1b=min{a，b}；（ii）aΔ2b=ab；（iii）aΔ3b=max{a+b-1，0}。

引理1[14]设*：[0，1]×[0，1]→[0，1]是连续的t-算子，若a∈（0，1），那么存在b∈（0，1）使得b*b≥a。

引理2设*：[0，1]×[0，1]→[0，1]是连续的t-算子，若a∈（0，1），那么存在b∈（a，1），使得b*b＞a。

证明令a∈（0，1），c∈（a，1），由引理1 可知，存在b∈（0，1）使得b*b≥c，因此，b*b＞a。

定义2设X是实数域上的线性空间，N是X×（0，+∞）上的模糊子集，*是连续算子。对任意的x，y∈X，

（1）对任意的t＞0，N（x，t）＞0；

（2）对任意的t＞0，N（x，t）=1⇔x=θ，其中θ 是X中的零元素；

（3）对任意的t＞0，当λ≠0 时

（4）对任意的t，s＞0，N（x，t）*N（y，s）≤N（x+y，t+s）；

（5）N（x，·）在（0，+∞）→（0，1]上是连续的且那么称N是X上的模糊范数，（X，N，*）是模糊赋范空间。若（1）改为：

（N1）对任意的t∈R，t≤0 时，N（x，t）=0；t＞0 时，N（x，t）＞0。那么N是文献[4]中定义的模糊范数。

下文中的模糊赋范空间不作特殊说明的，均为定义2 中的模糊赋范空间。类似于文献[5]，设（N，X，*）是模糊赋范空间，定义B（x，r，t）={y∈X:N（x-y，t）＞1-r}。

容易验证{B（x，r，t）:t＞0，r∈（0，1）}是在x处的一个邻域基。由此，模糊范数N可导出X上的一个拓扑，记为τN。显然τN为第一可数的，事实上，{B（x，1/n，1/n）:n=1，2，…}为x的可数局部基。

2 子集的有界性

该节主要介绍模糊赋范空间中模糊有界集、模糊强有界集以及模糊弱有界集的概念，并给出它们的刻画定理。

定义3设（X，N，*）是模糊赋范空间，A⊆X。

（2）若存在t0＞0，使得则称A是模糊强有界集；

（3）若对任意的t＞0，总有则称A是模糊弱有界集。

对任意的r∈[0，1]，x∈X，引入记号显然地，||x||1≡0。

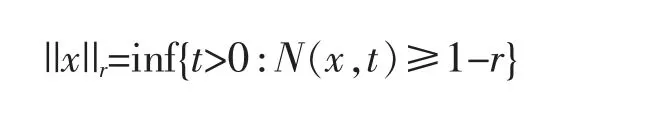
容易得到：

性质1设（X，N，*）是模糊赋范空间，A⊆X。

引理3设（X，N，*）是模糊赋范空间，A⊆X，r∈[0，1]。那么

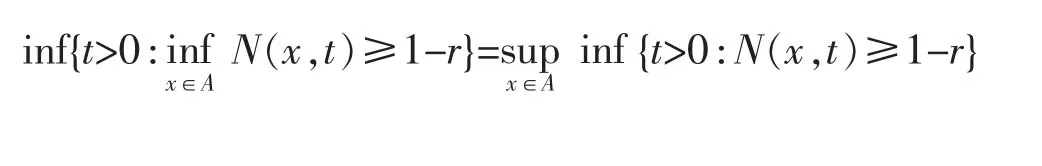
证明对任意的因而有

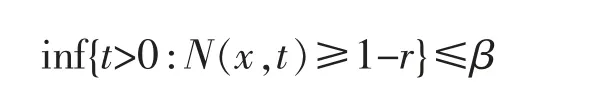
任取ε＞0，存在t0＞0，使得t0＜β+ε且N（x，t0）≥1-r，从而

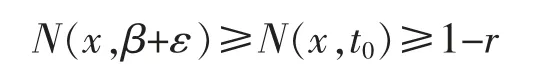
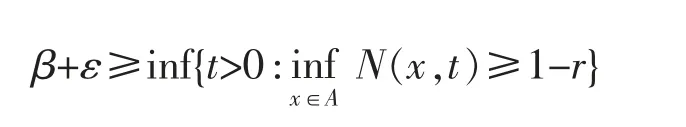
再由ε的任意性可知即

引理得证。

引理4设（X，N，*）是模糊赋范空间，A⊆X，r∈[0，1]。若

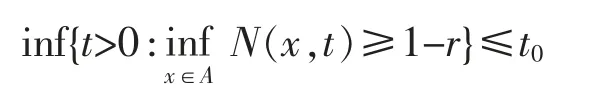
证明对任意的所以存在0＜t′＜t0+ε，使得由引理3 可知所以对任意的x∈A，N（x，t0+ε）≥1-r。由ε的任意性及N（x，·）的连续性可知，N（x，t0）≥1-r，从而

引理5设（X，N，*）是模糊赋范空间，对任意的x∈X，r∈（0，1），那么

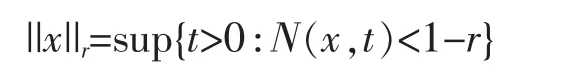
证明需证明inf{t＞0:N（x，t）≥1-r}=sup{t＞0:N（x，t）＜1-r}。

设A={t＞0:N（x，t）≥1-r}，B={t＞0:N（x，t）＜1-r}。任取t1∈A，t2∈B，则N（x，t1）≥1-r＞N（x，t2）。由N（x，·）关于t 的递增性可知，t1≥t2，则有inf A≥sup B。

再设inf A=α，sup B=β。对任意的δ＞0，β+δ∉B，则有β+δ∈A，从而inf A≤β+δ。由δ的任意性可知inf A≤β=sup B。得证。

定理1设（X，N，*）是模糊赋范空间，A⊆X。

（1）A 模糊强有界当且仅当存在t0＞0，使得对任意的

（2）A 模糊有界当且仅当对任意的r∈（0，1]，存在正数t0＝t0（r），使得

（3）A 模糊弱有界但非模糊有界当且仅当存在r0∈（0，1），使得当而当r∈（r0，1）时，存在t0＝t0（r）＞0，使得

证明（1）必要性易证，仅证充分性。假设对一切r∈[0，1]都成立。由引理3，

（2）设A模糊有界，则有对任意的r∈（0，1]，存在t0（r）＞0，使得由引理4 和上式即得

反之，对∀r∈（0，1]，存在t0（r）＞0，使得t0（r）。由引理4 可知，N（x，t0（r））≥1-r，所以从而由r的任意性，即得

（3）设A模糊弱有界但非模糊有界，则

（i）当r∈（0，r0）时因而对一切由引理3 有，

（ii）当r∈（r0，1）时故存在t0（r）＞0，使得于是由引理3，

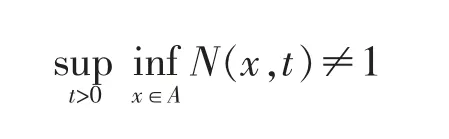
当r∈（r0，1）时，由于存在t0（r）＞0，使得由引理1-r}≤t0（r）。再由引理于是注意到r∈（r0，1），r0∈（0，1），可得所以即证A为模糊弱有界但非模糊有界集。

3 算子的紧性

该节介绍模糊赋范空间中的S－模糊紧算子以及相关定理。

定义4设（X，N，*）是模糊赋范空间，A⊆X。

（1）设{xn}⊆X，x∈X，若对任意的t＞0，满足则称序列{xn}收敛于x，而称x为{xn}的极限点，记为

（3）若A中的任一序列都有收敛的子列，则称A是模糊紧集。

（4）若A的闭包是模糊紧集，则称A是相对模糊紧集。

注：易证明，以上定义的概念与拓扑τN意义下相应的概念是一致的。

定义5设（X，N1，*1）和（Y，N2，*2）是模糊赋范空间，算子T:X→Y。

（1）若对X中的任一模糊强有界子集A，T（A）是Y中的相对模糊紧集，则称算子T是S-模糊紧的；

（2）若对X中的任一模糊有界子集A，T（A）是Y中的相对模糊紧集，则称算子T是模糊紧的。

定理2设（X，N1，*1）和（Y，N2，*2）是模糊赋范空间，算子T:X→Y。T是S-模糊紧的当且仅当对X中的任意的模糊强有界序列{xn}，{T（xn）}均有收敛子列。

证明先证必要性。假设{xn}是X中的模糊强有界序列，T是S-模糊紧算子，那么{T（xn）}是相对模糊紧集。由定义4 可知是模糊紧集，那么{T（xn）}有收敛的子列。

再证充分性。假设A是（X，N1，*1）中的模糊强有界集，下证T（A）是相对模糊紧集，即是模糊紧集。

设yn∈T（A），n=1，2，…，则存在Zm（n）∈T（A），使得当m→∞时，{Zm（n）}收敛于yn，存在mn，使得

取n==max{n¯，n0}，则当n′＞n=时，（3）式成立，且n′＞n0，即于是由（1）式可知

针对文献[4]意义下模糊赋范空间，文献[5－6]引入了算子的模糊有界、模糊强有界、模糊连续、模糊强连续等概念。类似地，这些概念可以引入到文中所定义的模糊赋范空间中。为方便起见，给出具体的定义如下：

定义6设（X，N1，*1）和（Y，N2，*2）是模糊赋范空间，算子T:（X，N1，*1）→（Y，N2，*2）。

（1）若对任意的r∈（0，1），x∈X，存在Mr＞0，使得对任意的t＞0，s＞t，当时，N2（T（x），s）≥r，则称算子T是模糊有界的。

（2）若对∀x∈X，存在M＞0，使得对任意的则称算子T是模糊强有界的。

（3）若对任意的xn∈X，存在x∈X，使得对任意的t＞0，当时则称算子T是模糊连续的。

（4）若对任意的x，y∈X，存在ε＞0，使得对任意的t＞0，N2（T（x）-T（y），t）≥N1（x-y，ε），则称算子T是模糊强连续的。

注：模糊强连续（有界）算子是模糊连续（有界）算子。

定理3设（X，N1，*1）和（Y，N2，*2）是模糊赋范空间，若T是模糊强有界算子，当A是模糊强有界集，则T（A）也是模糊强有界集。

证明因为A是模糊强有界集，则存在t0＞0，对任意的r∈[0，1]，都有由引理3 得，

由定理1，T（A）也是模糊强有界集。

定理4算子T是模糊有界的当且仅当对任意的x∈X，r∈（0，1），都存在Mr＞0，使得

证明先证必要性。设T是模糊有界的，那么对任意的x∈X，r∈（0，1），存在Mr＞0，使得对任意的t＞0，s＞t，当时，N2（T（x），s）≥r。任取α＞Mrinf{t＞0:N1（x，t）≥1-r}，即则存在0＜α′＜α，使得于是由定义6（1）可知，N2（Tx，α）≥r，从而inf{t＞0:N2（Tx，t）≥r}≤α。由α 的任意性，有

再证充分性。假设对∀x∈X，r∈（0，1），存在Mr＞0 使得（4）式成立。于是对∀t＞0 及s＞t，当由（4）式知inf{α＞0:N2（T（x），α）≥r}≤t。于是，inf{α＞0:N2（Tx，α）≥r}＜s，从而N2（Tx，s）≥r，所以T算子是模糊有界的。

定理5设（X，N，*）是模糊赋范空间，T1，T2是从（X，N1，*1）到（Y，N2，*2）的线性S－模糊紧算子，α＞0，那么T1+T2，αT1也是线性的S－模糊紧算子。

证明设{xn}是X中的模糊强有界序列，T1，T2是线性的S－模糊紧算子，由定理2，存在{xn}的子列{xnk}，使得T1（xnk），T2（xnk）都收敛。于是存在y1，y2∈Y，使得对任意的t＞0，

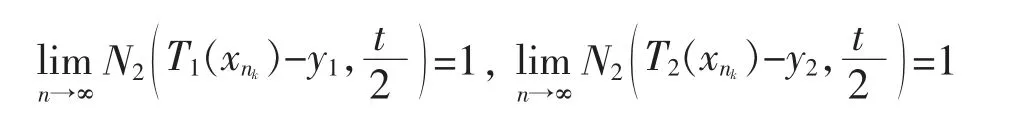
由（*）的连续性，可得

同样地，设{xn}是X中的模糊强有界序列，则{αxn}也是X中的模糊强有界序列。因为T1是线性的S－模糊紧算子，那么{T1（αxn）}有收敛的子列。即存在y∈Y，使得对任意的即所以{（αT1）（xn）}有收敛的子列，由此可见αT1是线性的S－模糊紧算子。

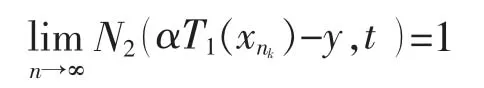
定理6设（X，N1，*1）和（Y，N2，*2）是模糊赋范空间，算子T:（X，N1，*1）→（Y，N2，*2）是线性的。T是模糊强连续的当且仅当T是模糊强有界的。

此处证明略。具体证明类似于文献[5]中定理3.5（ii）。

定理7设（X，N，*）是模糊赋范空间，T:（X，N，*）→（X，N，*）是满射的S－模糊紧算子，S:（X，N，*）→（X，N，*）是模糊强连续的线性算子，那么复合算子ST和TS都是S－模糊紧算子。

证明设{xn}是X中的模糊强有界序列，由T是S－模糊紧算子可知，{T（xn）}有收敛的子列{T（xnk）}。于是存在Ty∈Txnk，使得对任意的又因为S是模糊连续的，则有

即ST（xn）有收敛的子列，那么ST是S－模糊紧算子。

同样地，设{xn}是X中的模糊强有界序列，则存在t0＞0，对任意的r∈[0，1]，使得由引理3 知，由定理6 可知，模糊强连续的线性算子S也是模糊强有界的，则由定理3 可知，{S（xn）}是模糊强有界的。又因为T是S－模糊紧算子，所以{（TS）（xn）}有收敛的子列。由此可见，TS也是S－模糊紧算子。