双轴模拟式太阳敏感器的误差源分析*
2016-04-14王春宇吕政欣孙建波种会萱
王春宇,梁 鹤,吕政欣,孙建波,洪 帅,孙 艳,种会萱
(北京控制工程研究所,北京100190)
双轴模拟式太阳敏感器的误差源分析*
王春宇,梁 鹤,吕政欣,孙建波,洪 帅,孙 艳,种会萱
(北京控制工程研究所,北京100190)
双轴模拟式太阳敏感器(简称双轴太敏)基于四象限硅光电池,可同时实现太阳矢量两轴方向角的测量.针对装配环节偏差导致的双轴太敏姿态测量误差问题,提出了对双轴太敏掩膜玻璃通光孔与硅光电池间的中心偏移、旋转和倾斜以及光电组件安装偏斜等主要误差源进行定量分析的方法,为有效补偿双轴太敏各装配环节偏差奠定基础.
双轴;太阳敏感器;四象限;误差源
0 引 言
太阳敏感器可对太阳矢量相对于航天器的入射角进行高可靠、高精度检测,适用于帆板定向、卫星定姿等多种任务,为航天器应用最为广泛的姿态敏感器之一[1].基于四象限硅光电池[2]的模拟太阳敏感器可同时实现两轴太阳矢量角的测量,国内外很多研究机构均进行了研制.浙江大学研制的双轴模拟太阳敏感器[3](简称双轴太敏)采用机械加工式遮光罩,引入误差的环节较多,敏感器姿态测量精度仅为±1°;清华大学将信号处理环节的非线性转换到掩膜图案的非线性,研制了双轴太敏[1],可在双轴±62°视场范围内实现±0.2°的姿态测量精度;荷兰TNO-TPD公司[4]在双轴±64°视场范围内的姿态测量精度为±0.3°.然而,由于装配环节存在偏差,影响了双轴太敏的姿态测量精度,但尚未有文献对相关误差源及其影响进行定量分析,并对双轴太敏的姿态测量精度进行有效补偿[5].
1 双轴太敏工作原理
双轴太敏以四象限硅光电池为敏感元件.四象限硅光电池是在一片正方形硅光电池上光刻出4个独立的同尺寸同面积的光敏元素,如图1(a)所示.以硅光电池中心O1为原点,建立光电坐标系O1XSSYSSZSS,其中面XSSO1YSS与硅光电池光敏面重合,O1ZSS垂直光敏面向上.将分别位于面XSSO1YSS第一至四象限的光敏元素记为S1~S4.a、b分别为各光敏元素的边长和间隔.在四象限硅光电池正上方h处平行设置一带有边长为d的正方形通光孔的掩膜板,通光孔中心O2位于轴O1ZSS上,且其四边分别与轴O1XSS、O1YSS对应平行,如图1(b)所示.透过通光孔的太阳光线投射到四象限硅光电池上,在S1~S4上产生不同的光照面积,并分别输出与其光照面积成正比的光生电流.
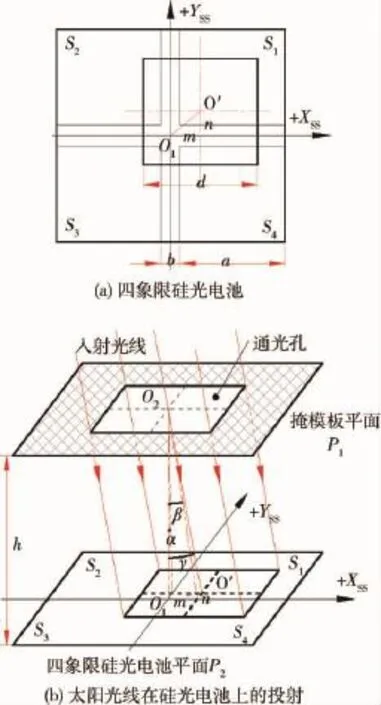
图1 双轴太敏工作原理Fig.1 Principle of dual-axial sun sensor
定义太阳矢量OS在面XSSO1ZSS内的投影与轴O1ZSS夹角为α,光线从O1XSS负方向入射时α为正;定义太阳矢量 OS在面YSSO1ZSS内的投影与轴O1ZSS夹角为β,光线从O1YSS负方向入射时β为正,如图1所示,则

其中,m、n分别为掩膜通光孔中心沿太阳矢量OS在面XSSO1YSS上投影O'在轴O1XSS、O1YSS的坐标值.由几何关系可知,硅电池各光敏元素输出光电流分别为
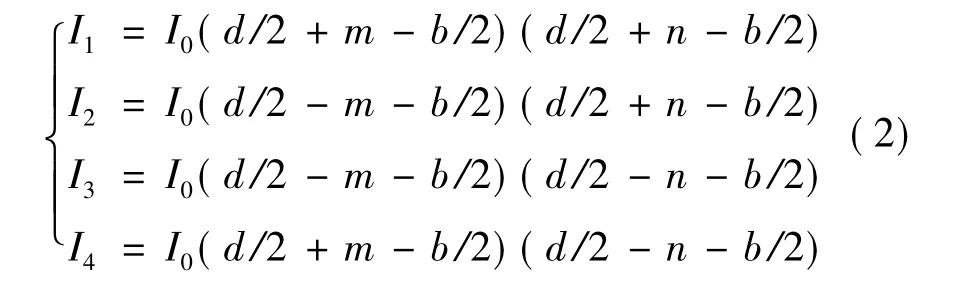
其中,I0=Imcosγ为硅光电池在该入射角下的响应率,Im为硅光电池在光线垂直入射时的响应率,γ为光线相对于硅光电池光敏面的入射角,可得

可知,通过检测硅电池各光敏元素输出电流,由式(3)分别计算出m、n,由式(1)计算出α、β.
2 双轴太敏误差源分析
由1节分析可知,为提高双轴太敏的姿态测量精度,需保证光电组件掩膜通光孔面与硅光电池光敏面平行、掩膜板通光孔中心与硅光电池中心沿硅光电池法线方向对准、掩膜板通光孔四边与硅电池坐标轴对应平行.但加工、装配等环节的偏差会对双轴太敏的姿态测量精度造成不同程度的影响.此外,光电组件安装在敏感器结构上,结构提供了敏感器的安装基准,并实现了光电组件坐标系(简称光电坐标系)和敏感器整机坐标系(简称结构坐标系)的对应转换.若光电组件在敏感器结构上安装偏斜,光电坐标系和结构坐标系下的太阳矢量角就会存在偏差.
2.1 光电组件装配偏差
对应1节所述原理对光电组件的装配要求,光电组件装配偏差主要由偏移、旋转和平面倾斜组成.
偏移是指掩膜板通光孔中心在XSSO1YSS平面上的投影与硅电池中心O1不重合,如图2所示.掩膜板通光孔中心坐标为(m0,n0,h),其中,m0,n0为掩膜板通光孔中心的投影与O1在O1XSS、O1YSS方向上的偏移.
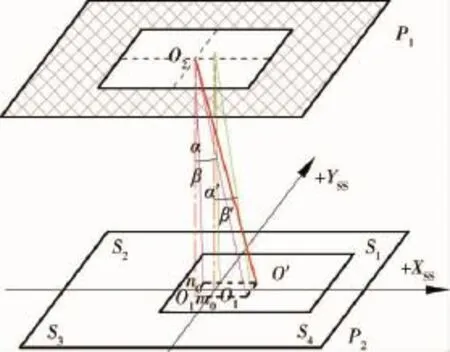
图2 偏移的影响分析Fig.2 Influence analysis of offset
旋转是指掩膜板通光孔中心在XSSO1YSS平面上的投影与硅电池中心O1重合,掩膜板绕过其中心的法线O1O2旋转角度θz,如图3所示,此时掩膜通光孔沿太阳矢量在硅光电池上的投影区域也绕其投影中心同方向旋转角度θz.

图3 旋转的影响分析Fig.3 Influence analysis of rotation
平面倾斜是指掩膜板通光孔中心在XSSO1YSS平面上的投影与硅电池中心O1重合,但掩膜板通光孔面与硅光电池光敏面不平行.如图4所示,在掩膜板理想位置P2中心建立坐标系XSS'O1'YSS',其中O1'在轴O1ZSS上,且轴O1'XSS'、O1'YSS'分别与O1XSS、O1YSS轴同向.平面P2与硅光电池光敏面P1平行且距离h,而实际装配时,可认为掩膜板实际位置P1为其理想位置P2先绕轴O1'XSS'旋转角度θx,再绕O1'YSS'旋转角度θy得到.此时,掩膜通光孔在硅光电池上的投影不再是矩形,而是根据太阳矢量两轴方位角的不同而不同的菱形.

图4 平面倾斜的影响分析Fig.4 Influence analysis of tilt
偏移、旋转和倾斜在不同太阳矢量角下会产生不同程度的耦合,为此,综合分析三者共同作用下,光电坐标系下太阳矢量角的测量误差.
掩膜板与硅光电池间距离h保持不变,在偏移、旋转和倾斜共同作用下,掩膜板首先沿O1'XSS'、O1'YSS'方向移动m0、n0,然后依次绕O1'XSS'、O1'YSS'、O1'ZSS'方向旋转θx、θy、θz,并考虑到在精密装配下,可认为 θx、θy、θz很小(<5″),则 cosθx= cosθy=cosθz=1、sinθx=θx、sinθy=θy、sinθz=θz,则坐标系XSS'O1'YSS'下,掩膜板通光孔四顶点1'~4'坐标为
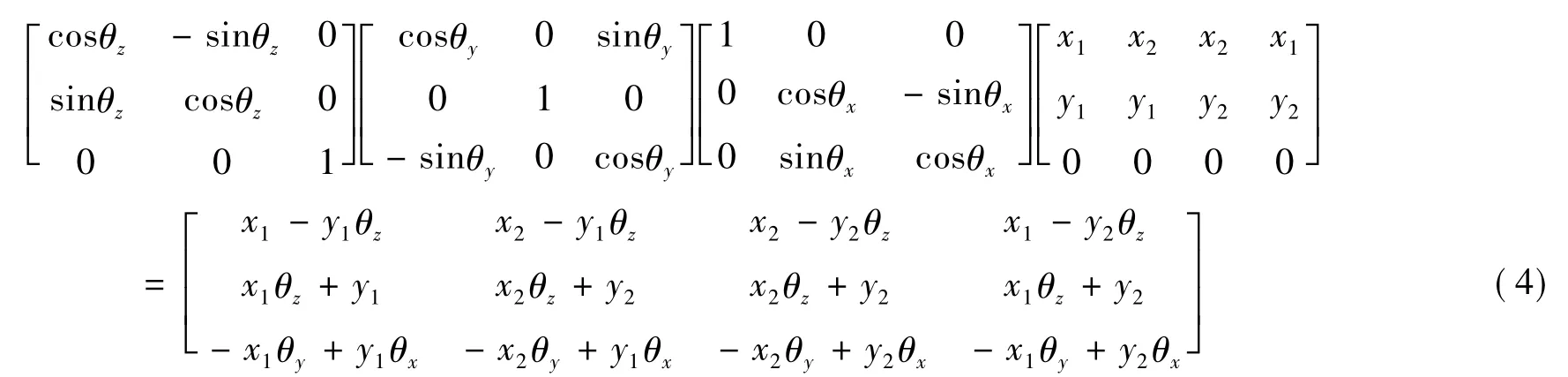
其中,x1=d/2+m0,x2=-d/2+m0,y1=d/2+n0,y2=-d/2+n0,则四顶点沿太阳矢量在XSSO1YSS平面上的投影1~4坐标分别为

其中,α、β分别为太阳矢量方向角的真实值.
为简化分析,设定在全视场范围内,1~4点分别位于S1~S4,将m0、n0、θx、θy、θz均视为小量,忽略二阶及以上小量,则硅光电池各光敏元素输出光电流关系为:

当太敏视场为双轴±45°,且旋转角为小量条件下,可认为|θxtanα-θytanβ|<<1,同时考虑到b<<d及式(1)和(3),则

其中,α'、β'分别为太阳矢量方向角的测量值.由式(7)可见,θz的影响可忽略.由于平面倾斜θx、θy的作用,太阳两轴方位角的检测产生耦合,且造成的误差随耦合轴矢量角的增大而增大;而偏移m0、n0对两轴太阳矢量角的检测不产生耦合.
2.2 组件安装偏差
双轴太敏存在机械零位、光零位和电零位等基准,如图5所示[6].结构坐标系OXYZ以敏感器安装基准孔下表面中心为坐标原点,OX轴正向指向敏感器出线方向,OZ轴垂直安装面向上;当太阳光沿OZ负方向入射时,即为机械零位,通常以机械零位为装配基准.光电坐标系O'X'Y'Z'以硅光电池中心为坐标原点,O'X'轴正向指向出线方向,O'Z'轴垂直硅光电池光敏面向上,当太阳光沿O'Z'负方向入射时,即为光零位;坐标系O1X1Y1Z1以硅光电池中心为坐标原点,O1X1轴正向指向出线方向,当太阳光沿O1Z1负方向入射时,硅光电池光敏元素S1~S4输出光生电流相等,即为电零位.根据太阳矢量角检测原理,本节忽略3个坐标系原点的不重合.理论上,三者应相互重合.实际装配中,由于光电组件在机械结构件上存在安装偏差,造成机械零位与光零位不重合;由于所采用的光电池各光敏元素响应率不一致和不均匀,造成光零位与电零位不重合.本节仅分析机械零位与光零位不重合,即光电组件安装偏斜对姿态测量精度的影响.
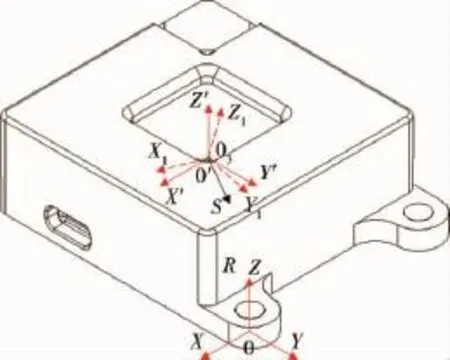
图5 敏感器各零位间的关系示意图Fig.5 Schematic diagram of sensor zero positions
组件安装偏斜包括硅光电池光敏面相对于机械安装平面的倾斜和旋转,采用坐标变换的方法对其进行分析.光电坐标系OX'Y'Z'分别绕轴OX'、OY'、OZ'旋转θxM、θyM、θzM后,与结构坐标系OXYZ重合.设太阳矢量OS在坐标系OX'Y'Z'下的两轴方向角为α、β,则矢量OS的坐标为[tanβtanα-1].在精密装配条件下,可认为旋转角θxM、θyM、θzM为小量(一般小于5'),由此,cosθi=1,sinθi=θi,(i=xM、yM、zM),并忽略高阶小量,则由坐标变换原理,矢量OS在OXYZ坐标系下的坐标为

当太敏视场为双轴±45°,且旋转角为小量条件下,可认为|-θyMtanβ+θxMtanα|<<1,则在OXYZ坐标系下,太阳矢量的俯仰、偏航角分别为

其中αM、βM分别为结构坐标下太阳矢量两轴方向角.由式(9)可见,θzM的作用使得太阳两轴方位角产生耦合,且造成的误差随耦合角的增大而增大,而θxM、θyM对两轴太阳矢量角的检测不产生耦合.
综合考虑式(7)和(9),可得在偏差m0、n0、θx、θy、θxM、θyM、θzM的作用下,并忽略二阶及以上小量,则双轴太敏输出可表示为

根据式(10)可设计基于内外参补偿算法,采用拟合方法确定m0、n0、θx、θy、θxM、θyM、θzM偏差参数,进而提高双轴太敏姿态测量精度[6];也可在确定双轴太敏姿态测量精度的前提下,由式(10)确定各装配环节偏差范围,从而对装配进行指导;也可由式(10)对各装配环节偏差引起的敏感器姿态测量误差进行估计,如当m0=n0=10 μm、θx=θy=0.1°、θxM=θyM=θzM=0.3°、h=2.75 mm时,α、β轴的测量误差分别为0.05°~0.81°、-0.40°~0.22°,其误差曲面如图6所示.

图6 各装配环节引起姿态测量误差曲面Fig.6 Measurement error of sensor introduced by assembly deviation
3 结论
双轴太敏在装配过程中会产生掩膜玻璃通光孔与硅光电池间的中心偏移、旋转和倾斜及光电组件安装偏斜等偏差,本文针对这些误差源对敏感器姿态测量精度造成的影响进行了定量分析,结果表明,在精密装配下,掩膜玻璃通光孔与硅光电池之间旋转的影响可忽略,而偏移因素和光电组件安装的倾斜因素不会造成太阳两轴矢量角的测量耦合.最后给出了装配偏差与双轴太敏姿态测量误差间的定量关系式,从而为双轴太敏的精度补偿、各装配环节的精度分配、装配偏差影响分析奠定基础.
[1]CHEN F F,FENG J.Analogue sun sensor based on the optical nonlinear compensation measuring principle[J].Measurement Science and Technology,2007,18:2111-2115.
[2]DELGADO F J,Quero J M,Garcia J,et al.SENSOSOL:MultiFOV 4-quadrant high precision sun sensor for satellite attitude control[C]//The 9thSpanish Conference on Electron Devices.NewYork:IEEE,2013.
[3]王俊,王昊,应鹏,等.四象限差动式模拟太阳敏感器设计[J].传感技术学报,2012,25(12):1659-1663.WANG J,WANG H,YING P,et al.Design of fourquadrant analog sun sensor[J].Chinese Journal of Sensors and Actuators,2012,25(12):1659-1663.
[4]BOOM K,LEIJTENS J.Mini and micro sensor systems:where small does not mean immature[C]// AIAA/AAS Astrodynamics Specialist Conference and Exhibit.Washington D.C.:AIAA,2008.
[5]樊巧云,张广军,魏新国.内外参数精确建模的太阳敏感器标定[J].北京航空航天大学学报,2011,37 (10):1293-1297.FAN Q Y,ZHANG G J,WEI X G.Sun sensor calibration based on exact modeling with intrinsic and extrinsic parameters[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(10):1293-1297.
[6]王春宇,梁鹤,吕政欣,等.一种可用于微小卫星的双轴微型模拟式太阳敏感器[C]//小卫星技术交流会.北京:中国宇航学会,2015.WANG C Y,LIANG H,LV Z X,et al.A micro dualaxial analog sun sensor for Microsatellite[C]//Technical Seminar for Microsatellite.Beijing:Chinese Society of Astronautics,2015.
Analysis of Error Sources Existing in Dual-Axial Analog Sun Sensor
WANG Chunyu,LIANG He,LV Zhengxin,SUN Jianbo,HONG Shuai,SUN Yan,CHONG Huixuan
(Beijing Institute of Control Engineering,Beijing,100190,China)
Based on a 4-quadrant silicon cell,the sun incident angle in two axes can be measured by a dual-axial analog sun sensor simultaneously.Aiming at measurement errors introduced by assembly deviation,the main error sources are analyzed quantificationally,such as the center offset,rotation and tilt between the aperture and silicon cell,and the incline of the optoelectronic component.Based on the presented analyses,the calibration can be realized with high precision.
dual-axial;sun sensor;4-quadrant;error source
V44
:A
:1674-1579(2016)01-0043-05
10.3969/j.issn.1674-1579.2016.01.008
王春宇(1986—),男,工程师,研究方向为光学敏感器设计、空间本底分析及抑制技术;梁 鹤(1981—),男,工程师,研究方向为光学敏感器信号处理设计;吕政欣(1977—),男,高级工程师,研究方向为光学敏感器设计;孙建波(1979—),男,高级工程师,研究方向为光学敏感器精密装配技术;洪 帅(1987—),男,高级工,研究方向为光学敏感器精密装配技术;孙艳(1975—),女,高级技师,研究方向为光学敏感器精密装配技术;种会萱(1973—),女,高级工,研究方向为光学敏感器精密装配技术.
*国家自然科学基金资助项目(51405016).
2015-06-26
