量身定做 与时俱进

胡军++卢莉英

[摘要]以上海“二期课改”上教版《九年义务教育教科书·数学》八年级下册中的“第二十一章代数方程”为例，通过介绍该章的内容，比较“二期课改”教材与“一期课改”教材、不同版本教材、不同国家课程标准在本章内容处理方式上的异同，总结出上海“二期课改”上教版《九年义务教育教科书·数学》八年级下册“代数方程”章节的特点.

[关键词]代数方程；初中数学；比较研究

上海“二期课改”上教版《九年义务教育教科书·数学》（以下简称“二期课改”教材）八年级下册中的“第二十一章代数方程”是在学生学习了一元一次方程、一元二次方程、二元一次方程组及简单的三元一次方程组的基础上的延伸.具体内容如下表1所示：

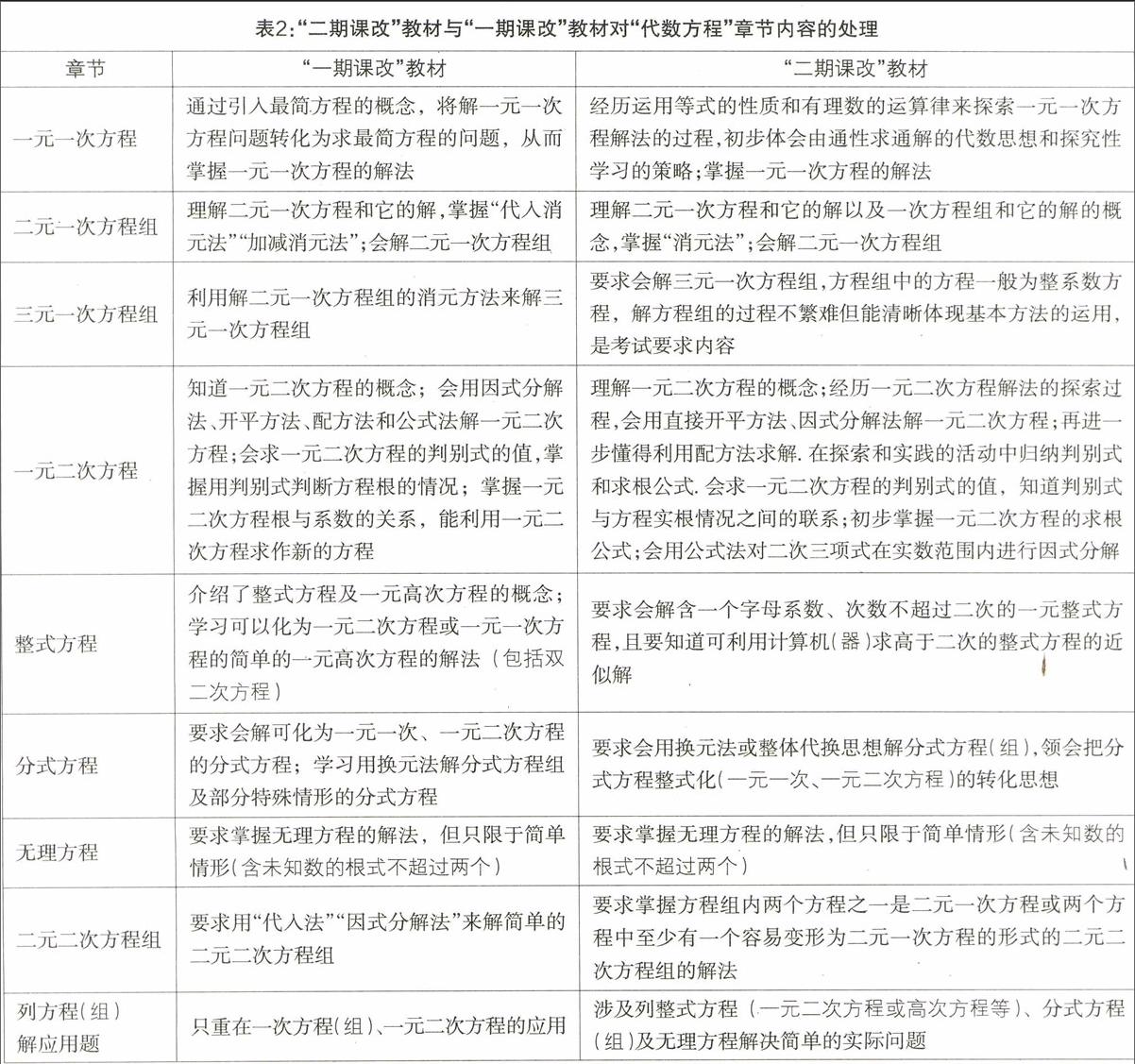
“二期课改”教材与“一期课改”教材对“代数方程”内容处理的比较

1.完整性，学生通过对“二期课改”教材中“代数方程”这章内容的学习，易形成对一元代数方程的系统感知，便于学生自主整理方程的概念系统，形成较为清晰的分类（图1）；而“一期课改”教材重视一元二次方程的应用，学生需要借助教师的帮助才能形成对一元代数方程的系统了解.

2.时代性.科学技术的迅速发展，简单繁琐的数学运算功能被弱化，而其思维训练功能得以进一步彰显.“二期课改”教材相较“一期课改”教材，本章中增设了二项方程的概念及解法，删除了双二次方程的有关概念（将此部分内容放入本章的“阅读材料”）.一方面从内容上丰富了高次方程的概念，另一方面将科学计算器引入课堂，利用现代化手段，引导学生经历解特殊高次方程的过程，体会从特殊到一般、从具体到抽象的思考过程，体验整体思想及解高次方程的“降次”策略，凸显了数学思维的训练.

3.应用性.“一期课改”教材仅仅侧重一元二次方程的应用，而“二期课改”教材在应用的范围上进一步拓宽，覆盖列整式方程（一元二次方程或高次方程等）、分式方程（组）及无理方程解决简单的实际问题，在应用范围上，比“一期课改”教材更广，更贴近生活，更富时代气息.

“二期课改”教材的本章内容与“一期课改教材”相关内容的比较如下表2：

“二期课改”教材与“一期课改”教材对“代数方程”编写特点的比较

上海“二期课改”教材中的“代数方程”内容与全国教材的设置及编排有较大差异.我们查阅了相关课程标准，比较如下表3.不难看出上海“二期课改”教材中的代数方程部分更系统，要求也更细致.

不同版本教材对“代数方程”相关主题内容的安排

我们又把“二期课改”教材中相应内容与部分省市所用的教材做了对比（表4）.通过比较，我们发现，“二期课改”教材代数方程部分相比其他省市内容多、要求高.

通过比较发现，上海“二期课改”教材中，“代数方程”章节的内容，无论从涉及的范围，还是从要求掌握的程度都远远超过这些经济比较发达的国家.那么，这部分内容是否会给上海学生带来额外负担呢？通过对师生的调查结果表明，担心大可不必，原因如下：

1.学生学习特点

上海是中国第一大城市，且已经成为一个国际大都市，它有着深厚文化底蕴.在这个城市成长、生活的孩子见多识广，他们乐于接受新事物，理解新概念，勇于攀登“高峰”，敢于尝试创新，在历次的PISA测试中，上海中学生成绩位居全球第一.他们的运算、画图、推理等基本技能及抽象概括、逻辑思维、空间想象、提出问题、分析问题、解决问题等数学基本能力与数学探究、建模的能力相对强些，在学习的过程中，有强烈的好奇心，会有“吃不饱”现象；在遇到困难的时候，愿意通过与他人合作交流，利用网络、DIMA平台等方式，以更好地理解问题，掌握知识点.

2.教师教学特点

上海吸引了大批优秀教师，他们爱岗敬业，业务精湛，把握教材的重点、难点，在他们的引领下，教师队伍整体实力比较强.教学氛围更讲究“授之以鱼不如授之以渔”，更注重学生的发展，学生学得轻松自在，由上而下的层层教研、科研活动，不流于形式，专心致力于研究教材教法、教育教学方法，推陈出新，全力打造温馨、和谐、有效的课堂.

3.教材适应学生、教师的特点

上海“二期课改”教材是根据学生和教师的特点“量身定做”的，主要体现在如下四个方面.

（l）系统性.“二期课改”教材中，“代数方程”整章内容完整，将整式方程、分式方程和无理方程全部融人其中.根据初中阶段学生的特点引入了他们能够理解的很多概念，从知识面上来说做到了系统性和完整性.教材抓住代数方程知识的主干部分，突出基本原理和通法，切实落实了义务教育阶段数学课程的基础性，学生通过初中阶段的数学学习能实现基本了解代数方程的脉络，掌握解代数方程的一些基本的方法，领会各种基本的数学思想，例如用字母表示数的思想、化归思想、方程思想、函数思想、数形结合思想、分类讨论思想等，这样的设置更有利于学生进入高中阶段的学习.

（2）递进性，“二期课改”教材中，“代数方程”章节的内容的处理符合学生的认知特点.让学生先接触基础知识，再在原有知识的基础上，增加新的内容，循序渐进，例如在七年级先认识分式方程，学会了可以化为一元一次方程的分式方程的解法，八年级第一学期学会了解一元二次方程，本章在一开始设置了对一元一次、二次方程相关内容的简单回顾和复习，目的是为本章内容做好铺垫.通过回顾来引导学生解含字母系数的一元一次、一元二次方程，引导学生探索可化为一元二次方程的分式方程的解法，使学生经历探索，领会分式方程“整式化”的化归思想.在此之后，学生的认知上了一个水平，引进无理方程的概念，他们也就很容易领悟无理方程的“有理化”，并且深刻明白“验根”的必要性，代数方程从教材组织上逐步推进新知，有利于学生学习，真正做到“螺旋式上升”.

（3）开放性，上海“二期课改”教材内容“套筒式”的安排，开放性强.首先，学习内容分为“基本内容”“拓展内容”和“专题研究与实践”.对于学有余力的学生，可以通过教材中的“阅读材料”及“拓展”深入学习，增强学习和研究兴趣.教育学家苏霍姆林斯基说：“如果学校培养不出有个性的学生，那么学校就没有真正的自己的学生”，其次，教材的编排满足了不同学生的需求.学过了代数方程中的基本内容，学生可以根据自身的学习情况，从教材中选择感兴趣的内容开展自主学习或者合作交流学习.学校也可根据学情，自主安排这一部分的教学.例如学生可以自主阅读本章“阅读材料”，了解两类特殊的一元高次方程及其解法，领会解一元高次方程的基本数学思想和方法，增强对一元高次方程进行学习和研究的兴趣.

（4）实用性.现代信息技术的迅速发展和广泛普及，迫切要求数学课程必须大力加强现代信息技术的应用，使现代信息技术成为学生学习的有效手段和工具，成为获取信息资源和开展学习交流的广阔平台，要求数学课程内容比以往更“实用”.本章在介绍二项方程解法时引入了计算器，让学生在计算器环境下自主学习，实验、探索和研究，与时代相符合且丰富了学生的学习方式，计算器的引入，方程（组）的应用部分显得更贴近生活、贴近实际.本章的最后，设置了方程（组）的应用，此时，学生代数方程的知识体系已趋于完整，建模空间更为广阔，更体现了数学的实用性，也更有利于学生思维的训练，

俗话说：十个手指有长短.由于地域等各方面影响，学生在数学学习领域存在差异是毋庸置疑的.著名数学家勒内·托姆（Rene Thom）曾指出：数学的学习主要应是一个自发探究的过程.蔡元培先生曾说：“教育是帮助被教育的人，给他发展自己的能力，”通过以上研究比较，可以说上海“二期课改”教材中的“第二十一章代数方程”真正做到了“量身定做、与时俱进”。endprint