基于置换思想的代数方程求解理论探析
2019-01-02赵增逊
赵增逊,马 梅,王 伟
(陕西铁路工程职业技术学院 基础课部,陕西 渭南 714000)
1545年G·卡尔达诺出版《大术》,至此,历经数千年后,数学家解决了四次以下的代数方程求解问题[1]1-14,306-330。此后,数学家致力于解更高次代数方程[2]79-86。Lagrange提出用置换思想解代数方程,代数方程求解由寻找计算技巧转变为寻找通用方法[3]1-128,从寻找求根公式变为寻找预解式[4]。Lagrange提出的一些重要概念,如域、置换群等,促使代数方程求解问题最终解决[5]。很多研究者,如伊夫斯[6]208-211、李迪[7]302-305、R·R·Hamburg[8]等,指出Lagrange的杰出贡献是提出了置换思想。笔者深入研究Lagrange于1770—1771年发表的法语论文RéflexionssurlaRésolutionalgébriquedeséquations原文[9]205-421,尝试还原Lagrange置换思想的产生过程。
1 置换思想产生的原因
事实上,到Lagrange时期,解代数方程已经取得了一定的成果。Cardano,Ferrari,Tschirnhaus,Bezut,Euler等采用各自的方法,已经解决三次、四次方程的求解问题。Lagrange发现,他们的方法区别在于运算技巧,而本质相同。Lagrange深受启发,提出辅助方程理论,即解三次方程需要预解一个二次的辅助方程,解四次方程需要预解一个三次的辅助方程,这样,四次以下的方程可以通过解辅助方程而得到原方程的解。而在后续的研究中,Lagrange发现解五次方程需要预解一个二十四次的辅助方程(虽然其可化为六次)[10]27-59,很显然,五次方程无法通过解辅助方程而得到解。此时,寻找一种区别于运用计算技巧的方法势在必行。置换思想应运而生。
2 置换思想产生过程
2.1 对已知解法的思考
解代数方程的关键是解其辅助方程。Cardano得到的三次方程的辅助方程为
不失一般性,设
x3+mx2+nx+p=0
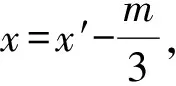
x′3+n′x′+p′=0,
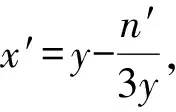
(1)
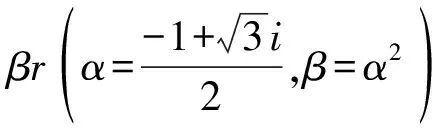
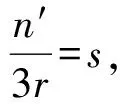
因此
即
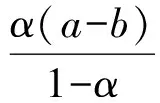
(2)
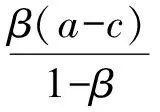
(3)
式(2)、式(3)联立,
(4)
知道
x3-1=(x-1)(x-α)(x-β)。
(5)
对式(5)求导,
3x2=(x-α)(x-β)+(x-1)(x-β)+
(x-1)(x-α),
令x=1,α,β,有
(6)
将式(6)代入式(4)有
(7)
r即是辅助方程的根y的值,而对于式(7),可以任意交换a,b,c的位置,即
即辅助方程的根有6个,那么原方程的辅助方程必为六次。关于y的方程次数依赖于预解式在原方程根下置换的不同值的个数[9]213-217。
既然辅助方程的次数由预解式在原方程根下置换的不同值的个数确定[11]1-20,那么需要找到这个预解式,进而确定辅助方程的次数,构造相应的辅助方程,通过解辅助方程解原方程,其关键因素是置换思想。
2.2 用置换思想解代数方程
Lagrange尝试用置换思想解代数方程。设
x3+mx2+nx+p=0
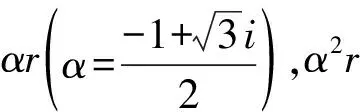
r=Aa+Bb+Cc,
则
αr=αAa+αBb+αCc
应等于其他5个中的1个。若
αr=Ab+Bc+Ca,
则C=αA,B=α2A,α3A=A。令A=1,则C=α,B=α2,若
r=a+αb+α2c,
s=a+αc+α2b,
则辅助方程的根为r,ar,a2r;s,as,a2s。设辅助方程是关于y的方程,由
(y-r)(y-ar)(y-a2r)=y3-r3,
(y-s)(y-as)(y-a2s)=y3-s3,
故有
y6-(r3+s3)y3+r3s3=0。
由根与系数关系
a+b+c=-m,
ab+ac+bc=n,
abc=-p,
可知
r3+s3=-m3+9mn-27p,
r3s3=(m2-3n)3。
故辅助方程为
y6-(-2m3+9mn-27p)y3+(m2-3n)3=0。
令z=y3,得
z2-(-2m3+9mn-27p)z+(m2-3n)3=0。
(8)
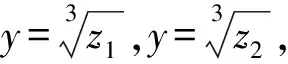
与a+b+c=-m联立方程组,得到原方程的根,
Lagrange用置换思想顺利得到了三次方程的解。解方程关键是解辅助方程,确定辅助方程次数的核心是找到合适的预解式。
3 用置换思想求解代数方程的内涵
一般意义上讲,解代数方程就是解辅助方程,需要寻找一个预解式,该预解式在原方程根的置换下取不同值的个数即为辅助方程的次数。如果解n次方程能得到一个r(r 事实上并不简单。Lagrange尝试用置换思想解n次(五次及五次以上)代数方程,发现r次的辅助方程并不好找。但运用置换方法解代数方程的思想已经形成,代数学家开始按这种思路解高次的代数方程,Gauss将它运用在分圆方程上取得了辉煌的成就,Ruffini继续了Lagrange的工作,最终宣布五次及五次以上代数方程一般没有根式解,Abel给出了五次及五次以上代数方程没有一般解的证明,Galois最终取得了解代数方程的胜利。 用置换思想解代数方程是一元代数方程求解史上的伟大发现之一,直接动因是Lagrange解五次及五次以上代数方程,它也是Lagrange辅助方程理论的直接结果。置换思想是代数方程求解发展到一定阶段的必然产物,是Lagrange经过认真计算、缜密思考、严格实践得出的。4 结束语
