数形结合思想在高中数学教学与解题中的实践

☉江苏省黄埭中学 蔡俊

数形结合思想在高中数学教学与解题中的实践

☉江苏省黄埭中学 蔡俊

随着社会经济的不断发展进步，学校教育的不断改革创新，越来越多教师开始高度关注到数形结合思想在数学教学与解题中的应用.数形结合思想作为一种科学的解题手段，通过合理的应用能够有效提高解题效率和数学综合能力.本文将进一步对数形结合思想在数学教学与解题中的实践展开分析与研究.

目前是一个经济全球化时代，学校教育的发展要与时俱进，不断进行深化改革.高中数学教师在教学过程中要注重数形结合思想的高效利用，要引导学生在解题过程中积极利用数学结合思想，这样有利于使烦琐抽象的数学问题变得更加简单直观化，让多元化数学理论知识得到科学整合，学生能够充分掌握理解数与形之间的逻辑关系，快速准确的进行解题，从而提高他们的自信心与学习兴趣.

一、数形结合思想在高中不等式与方程中的具体应用

众所周知，坐标系作为高中数学普遍应用的图形.学生在解不等式与方程数学题时，要合理运用到坐标系的数学知识，这样有利于快速准确的进行解题.学生在面对比较复杂抽象的函数时，通过将其成功变换成图形形式，能够有效降低函数问题的难度，利用最短的时间寻找到解题方向或者得出最终的结论.

例1已知1≤x+y≤3，-1≤x-y≤1，求4x+2y的值域.

在解决这道有关不等式的题目时，数学教师可以引导学生利用数形结合的方法，首先建立起直角坐标系，然后作出不等式所表示的区域，如图1所示.

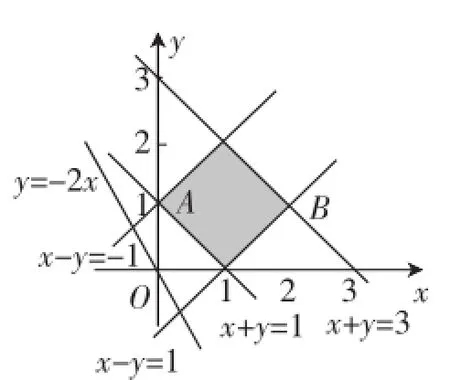
图1

分析：我们根据图1可以明确看出，两个不等式互相组成了一个平面区域，x与y之间并不是相互独立的关系，它们是由不等式组决定的相互制约关系.当y取得最大或者最小值时，对应的x并不能同时取得最大或者最小值，相反亦然.数学教师在讲解类似题目时，要让学生充分明白x与y之间的关系，从而得出正确的取值范围.

点评：不等式问题的解答，往往会使用到构造法，学生要经过构造出二次方程、构造函数以及构造图形，然后合理采用数形结合思想去解决此类问题.不等式问题转化为图形表示，能够让学生一目了然地看出某值的取值范围，求出正确的答案.科学利用图形能使原本复杂的数学问题变得简单直观化，从而在第一时间解决问题.

例2已知方程sin2x=sinx，求出它在区间（0，2π）内的解的个数.

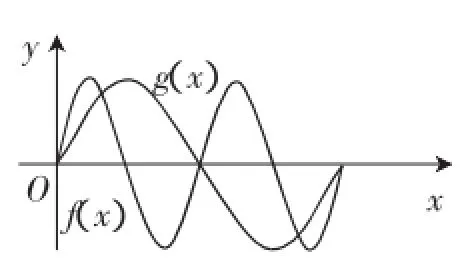
图2

解：如图2所示，在同一坐标系内，画出函数y=f（x）= sin2x，x∈（0，2π），g（x）=sinx，x∈（0，2π）的图像.sin2x=sinx在（0，2π）内的图像存在三个交点，所以由此可知，sin2x=sinx在区间（0，2π）内存在3个解.

分析：学生们在解此类方程时，教师可以向学生讲解到方程f（x）=g（x）的问题能够转化为两个函数y=f（x）与y=g（x）的交点问题，特别是在学生遇到解方程近似值时，通过运用这种方法能够高效的进行解题.

点评：方程式又可视为函数式，学生在遇到方程问题时，要将其转换为函数问题，因为每一个方程势必都会存在着一个与之相对应的函数图形，通过画出正确的函数图形，能够帮助学生快速解题，省去很多不必要的解题麻烦，从而节省更多时间，提高学习的质量和效率.

二、数形结合思想在高中集合中的具体应用

教师在讲解到集合这一章节内容时，要合理利用数形结合思想，让学生能将集合试题成功转化为简单明了的图形关系，根据图形快速的求出集合解集.图形使集合问题变得更加的具体化以及直观化，学生要掌握好运用几何图形、数轴以及文氏图去解决集合问题.

例3已知集合C=｛x|x2-5x-6＜0｝，D＝｛x||x-2|≥2｝，求出C和D之间的交集.

解：根据题意可知，C=｛x|-1＜x＜6｝，D=｛x|x≥4或x≤0｝.由图3可知，C与D的交集为｛x|-1＜x≤0或4≤x＜6｝.

图3

分析：在解此类集合问题时，学生要先分别求出集合C与集合D，接着再按照解出的集合作出相对应的数轴，在图上标记出集合C和集合D，根据上图学生可以直接得出集合的公共部分，求出最后的解集.通过利用数轴图形的方式，能够帮助学生快速的求出集合问题答案.

总结：教师要引导学生积极运用集合思想将问题进行变换，采用图形简单直接的方式运算集合问题，通过把数与图形有效联系在一起，运用图形语言高效地解决集合问题.

三、数形结合思想在高中函数中的具体应用

众所周知，函数作为高中数学的重点章节内容，受到了全体师生的高度重视.要想有效提高学生的函数解题能力，就必须加强学生数形结合思想的运用，要让函数问题复杂的公式变得直观化以及简单化.

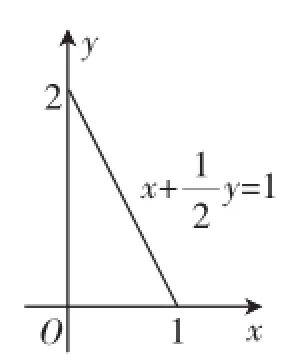
图4

点评：高中数学函数最值题型是一种比较重要的数学题目类型，教师要想提高学生对于此类题目的解决效率，就必须引导他们合理的应用数形结合的方法，通过画图去直观的分析问题，从而高效的解决问题.

四、数形结合思想在高中数列中的具体应用

数列作为一种较为特殊的函数，数列问题的解答可以通过运用数形结合的方法.学生除了要充分掌握好各项数列公式之外，还必须了解到数列与函数的关系.

例5设等差数列｛an｝的前n项和为Sn，其中a3=12，S12＞0，S13＜0，那么请求出在S1至S12中哪一个值是最大的，同时要说出具体原因.

解：由题意可知，数列｛an｝为等差数列，设Sn=An2+Bn（A，B分别是常数，其中A不等于0），那么就可得出Sn的图像是分布在二次函数y=Ax2+Bx的图像上，并且此图像经过坐标原点.题中条件说到S12＞0，S13＜0，那么就可以求出y=Ax2+Bx的图像上存在两点，分别是（12，S12），（13，S13），它们的位置在x轴的上方和下方.证明二次图像的开口向下，图像经过原点（0，0），如图5所示.我们假设图像与x轴的另一个交点为（m，0），并且12＜m＜13，可求出6＜＜6.5，最后得出图像对称轴的方程为x=.由于n∈N*，所以在S1至S12中，S6的值是最大的.

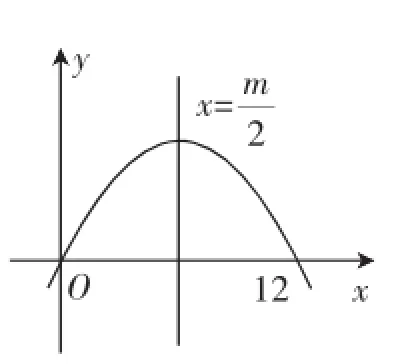
图5

点评：教师在讲解到此类函数问题时，既要教导学生要牢记各个函数公式，充分掌握理解数列与函数之间存在的关系，还要利用数形结合思想高效的解决问题.

五、数形结合思想在高中复数中的具体应用

高中复数内容也是一个重要的教学章节，学生在解决此类问题时，会普遍运用到数形结合思想，因为所有复数都可以通过平面直角坐标系进行表示，复数问题的解答与几何图像以及三角函数紧密的结合在一起.

例6存在|z-2|=3，请求出z的模的最小值与最大值.

解：由题意可知，|z-2|=3，那么复数z到（2，0）的距离为3，如图6所示，此图像的圆心点为（2，0），圆直径为6.z的模表示的是复数z到坐标原点的距离，这样根据图中就可以求出|z|的最小值是1，最大值是5.

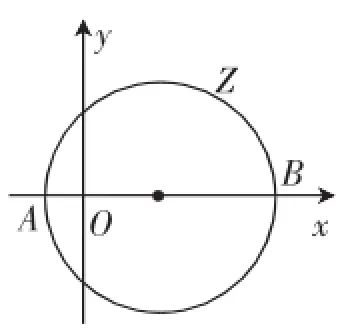
图6

点评：学生在解决此道复数题时，倘若采取的是代数形式，就会发现题目解答很烦琐，但是利用数形结合思想，就能够简单直观地用几何图形将复数表示出来，这样可以节省更多的解题时间，提高学生的解题效率.

六、数形结合思想在高中排列组合中的具体应用

排列组合作为高中数学的重点内容之一，学生在解决此类问题时需要结合实际生活，保证解题的逻辑性和灵活性.学生要充分了解排列组合问题与实际生活的关系，注意知识之间的内在联系，灵活应用数形结合思想进行解题.

例7已知一个圆周上存在10个点，那么将这10个点作为端点的弦在圆内部最多能够形成几个交点？

分析：众所周知，圆内部的任意两条弦都可能不存在交点，如图7所示，圆周上任意四点总共可连接起6条弦，有且仅有一个在圆内部的交点.学生在解答此题时，要想保证这些弦在圆内部的交点最多，那么就可以令这些交点互不相同，通过有效建立起一个圆上四点组与弦在圆内部的交点一一对应，不同的四点组相对应的交点不同，相反不同的交点对应不同的四点组.最后可求出圆周上10个点能够有效形成的不同四点组个数为N== 210.因此，以这10个点为端点的弦在圆内部最多能够形成210个交点.

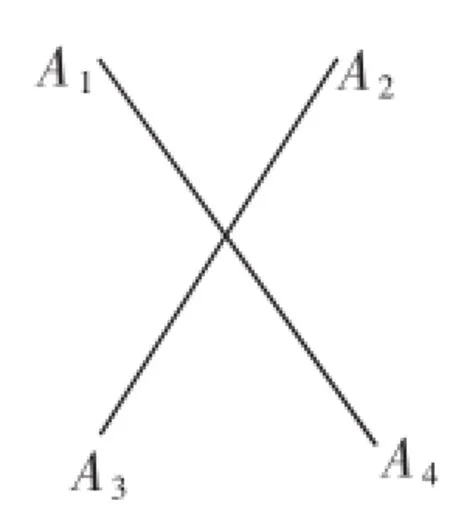
图7

点评：排列组合问题的解答，通过作图的形式能够使其简单明了化，学生只要整体把握其规律，利用好知识之间的内在关系，学会数形结合方法的灵活运用，就能够提高此类题目的解答效率.

综上所述，要想有效提高高中数学的教学质量和效率，培养学生各类题型良好的解题能力，就必须高度关注数形结合思想在数学教学与解题中的创新应用.我国伟大的数学家华罗庚先生也曾说过：“数缺形时少直观，形少数时难入微，数形结合百般好，割裂分家万事休.”因此，在高中数学教学过程中，教师和学生要学会灵活运用数形结合思想，让数学复杂抽象的数字公式变得更加的简单化、直观化，运用图形的方式使之呈现出来，也就让各类型的数学题从繁到简、化难为易，最大程度地提升了学生的解题效率.Z