小议课堂教学游离现象的表象和思考

☉江苏省仪征中学 曹远慧

小议课堂教学游离现象的表象和思考

☉江苏省仪征中学 曹远慧

课标指出：教师要引导学生在课堂教学中讨论、分析、建构，积极发展学生的思维，加强师生交流、生生合作，提高学生解决问题的有效性.从现阶段教学实际来看，特别是公开课、展示课教学，笔者认为教师在教学过程中往往追求了学生对于自主探究效果的设计，而忽视了讨论交流是否有效？合理？必须？出现了不少游离的现象.这种游离现象，其表现形式、产生的原因以及如何在教学中面对，笔者通过本文进行一些浅显的分析，与读者一起交流.

一、游离现象的具体表现

1.课堂讨论的内容跨度较大，讨论结果却收效甚微

课堂教学的讨论要符合学生数学认知心理预期，超越其预期的讨论是不合实际、无效的，甚至有时起到反作用.

案例1《概率》概念

在上这节概率的新课教学时，授课教师针对学生对此概念不易掌握，且易与自身已有的知识发生混淆的情况，在上课时拿出下面的一些相关问题，以供学生利用学习小组形式进行讨论研究，并加以指引，以图“催化”学生建构正确的概念图式.

题：通过对表1、表2、表3（限于篇幅，仅附表1，其余参见教材P112∽P113）的阅读和分析，请思考一下如何由随机事件的频率来确定其概率值.

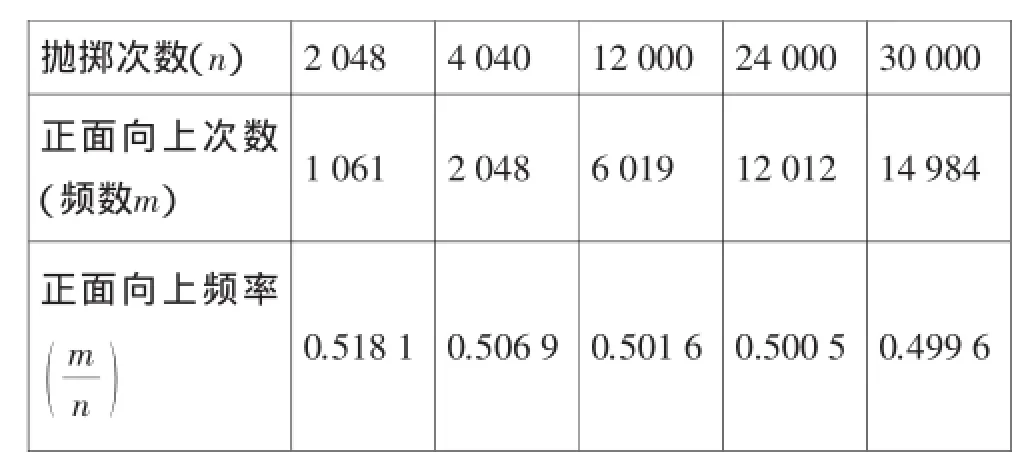
表1 ：抛掷硬币试验结果表

经过约十分钟思考和讨论后，各学习小组纷纷发表了意见.

小组1：认为概率值是把上述所有的频率值相加求平均值，还进行了一定的检验，比较接近.

小组2：对于小组1的认知，我们认为有问题，不能简单地通过所有频率值相加求平均值来计算，应该通过更多的试验来进行说明.

小组3：前两组说的都不完全正确.每一次不同的试验都可以得到不同的频率值，而且通过简单的思考，我们就能发现，这样的频率值是不可能完全相同的，随着试验次数越多这样的频率值应该更接近于真的概率值，我们可以做很多很多次的试验来验证.

师：等小组讨论之后，教师开始对不同组的错误观点进行一一指出，对于小组1、小组2所说的通过求平均值来求解概率还是不精确的，小组3的想法还是不错的，但是做无数次的试验不切合教学实际，因此通过这样的试验给出概率的定义：这种探究后的实施是比较自然和水到渠成的.这就逐渐清晰地表明：事件A发生的频率总接近的常数是概率.

但是这种讨论还是有一定问题的，因为现阶段中学数学对于无限次试验和极限定义的使用都仅仅是描述性的，并没有大学严密性的“ε-N”方式，这就让上述小组的讨论显得有很大的困难，试想在范畴不确定的形态下讨论，很多时候是无意义和低效的.

说明：对于上述概率概念教学，笔者认为这种使用实验教学的方式是正确的，其最大的问题是使用试验这种非形式化手段下的如何阐述频率和概率间的关系是不足的.笔者举一个案例：我们都知道函数的概念历经了上百年时间形成的，期间有着各种曲折和变换，如果在高一函数概念教学中不断去比较高中教材中的函数概念和初中函数概念，这种比较就犹如上述在没有范畴和背景下的盲目讨论，从而将课堂教学带进一种“讲不清、道不明”的游离状态.

2.课堂讨论的内容有失妥当，讨论思路形散神也散

单墫教授在研讨活动中曾经指出，我们的教学不要给学生设计圈套，只要学生能掌握数学知识的本质就是好的.从中学教学的实际来看，笔者发现中学教师往往对于问题的设计更喜欢设计为什么？而这种为什么的背后恰恰是对知识更为深刻的挖掘，但切记注意分寸，不能太过.否则易陷入讨论的误区.给出一个案例：

案例2已知f（x）=ax2+cx，且1≤f（1）≤3，-1≤f（-1）≤1，求f（2）的取值范围.（教材习题）

在复习线性规划课时，某教师给出了这样的一个问题，请同学们首先对于问题进行求解.教师对其的本意是希望学生从线性规划的角度去思考解决.但是由于教学准备不充分，学生却从另外的角度给出解答：

①+②，得0≤2a≤4，即0≤4a≤8，②×（-1），得-1≤c-a≤1，（记为③式）

①+③，得0≤2c≤4，故而代入f（2）=4a+2c得0≤f（2）≤12.

解法2：f（2）=4a+2c=3f（1）+f（-1），由已知可得3≤3f（1）≤9，-1≤f（-1）≤1，

故两式相加可得2≤f（2）≤10.

说明：如教学到此处教师直接截住，本课还能回归到正确的道路上，但令笔者不解的是，该教师开始组织学生对于上述两种不同的解答开始进行分析讨论，目的是想最后引出问题最一般性的线性规划的解决方案.对于上述两种不同解法的讨论持续了十来分钟，不断有学生对此提出不同的意见，这种形态热闹、却失去课堂精髓的讨论，使本课初始阶段失去了教学要揭露的本质——线性规划.可以这么说：我们发现此处的讨论是游离于本课核心（线性规划复习课）之外的，而且这种讨论既没有神，而且也无形，对于教学是不合适的.笔者认为，应该这样设计更为合理：

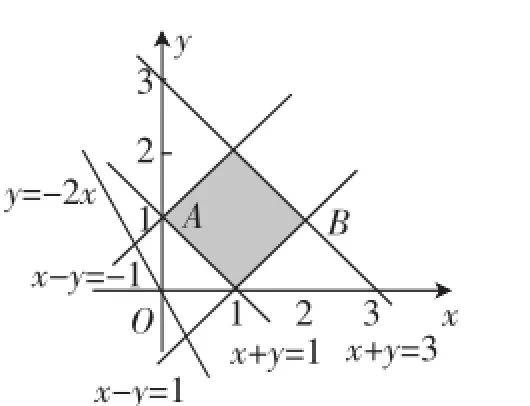
图1

然后请学生对比给出的解法2并与之讨论，利用代数解决方式和几何解决方式相互对比，得出正解形态下的线性规划的作用和有效性.在正解形态下的讨论，才是体现为什么我们选择线性规划的合理性，才是这一知识体现的价值所在.

二、防止游离现象的两点思考

从上述案例中，我们发现游离现象出现在教师对课堂教学的设计中.这种设计的表象，可以体现在很多方面：如讨论是否合理？有些讨论是否必要？教师自身对数学知识的理解和掌控？主流知识和非主流知识的区分？等等很多方面.因此，笔者认为对课堂教学如何避免出现游离需要关注以下两个方面：

1.首先教师应对课堂教学内容实施的必要性、可行性作出正确的研判

教训游离其实也是一种对知识不确定的表象，这尤其对教师而言是一种最基本的专业诉求.从人本理论的动机角度可以知道，教与学最基本的动力体现在三个方面实现：第一是美学的价值，第二是一种尊重的价值，第三是一种实现自我价值的需求.那么课堂教学也逃不出这样的行为.

要避免课堂教学的游离行为，首先需要对教学做出最基本的本质理解，这种理解笔者认为是对数学形式化过程和结果背后的一种深刻认知，只有深刻认知了这些形式化的数学结论，那么教师在课堂教学的设计中，才不会将课堂教学驾驭在正常的范畴之外.笔者举一个问题：

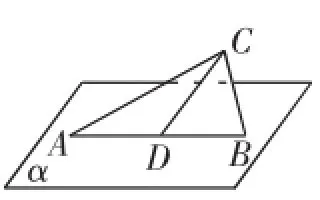
图2

问题1：如图2，平面ABC⊥平面α，D为线段AB的中点，AB=2，∠CDB=45°，点P为面α内的动点，且P到直线CD的距离为，则∠APB的最大值为___________.

分析：在解决本题过程中，首先要解决点P的轨迹问题，这种空间几何的截口曲线问题，是教材最本质的圆锥曲线概念的阐述.对于这一本质的解释，其实需要不少时间，不适宜在短短的本题讲解时进行拓展研究，更适宜在后续教学思考中引导学生进行知识的挖掘，因此笔者认为对这一问题的挖掘和研究需要做出可行性的设计，这样就避免了问题在课堂教学中始终处在对圆锥曲线本质深究的“游离”中.

2.其次教师应对课堂突发情形合理掌控，以及对讨论的结果进行适时评价

从本文所列举的案例二，我们发现正是因为教师对所要涉及的问题准备不充分，导致了在课堂初始阶段，对非核心知识进行了长时间的探讨，使得课堂教学游离在核心教学之外.

换句话说，对突发事件的一种掌控，其实也是教师在教学设计的时候的一种全面性的思考.在教学一线多年，笔者也曾因为对教学设计考虑不全面，而犯下过这样的错误.随着教学经验的增加和积累，笔者发现若再遇到类似的问题，教学中可以坦荡荡的告诉学生，这并不是本课所研究的重点，对于你所感兴趣的问题，我们可以在课后再进行研究，从而避免的课堂教学的游离.笔者再举一个问题：

问题2：若2x2+y2=1，则2x+3y的最大值为___________.

分析：本题教学中学生给出了不少的解决方法，诸如几何意义的方法、三角换元的方式、柯西不等式的方式等等，教师首先在设计之初要知道本题多样性的解决方式，并且要对其进行一一合理评价，要避免学生不同突发思维给出的不同方式，只有合理了解才能避免教学的“游离”.

最后还要指出，对于学生的各种讨论结果都需要给出恰当的评价.评价是课堂教学必不可少的环节，它让教师的课堂教学走在了最为正确的流程之上.比如本文中所举的部分案例，教师对其进行了部分评价，这种评价既肯定了学生的主动性、创造性，也为其后续发展自主学习的能力做出了一定的评判，这同样是让课堂教学走在正确的道路上，而没有游离.

综上所述，本文对于课堂教学游离的原因和一些情况进行了浅显的分析，着重指出了课堂教学为什么会出现游离的情况，并从自身教学经验的角度，提出了解决游离状态的一些思考，如：加强教学设计、考虑全面，避免发生课堂教学的不常规意外；删减不必要的一些讨论，让课堂教学走在最为正确的、最核心的道路上.限于篇幅以及笔者才疏学浅，不足之处，恳请读者批评指正.

1.弗赖登塔尔.作为教学任务的数学［M］.陈昌平，唐瑞芬，编译.上海：上海教育出版社，1995.

2.施良方.学习论（第二版）［M］.北京：人民教育出版社，2001.Z