巧添一高 难题不难①——解一般三角形的应用题简析

黄双华



巧添一高 难题不难①
——解一般三角形的应用题简析

黄双华

(广东省阳江市实验学校，阳江 529500)

求解一般三角形，通常通过添加高线将原三角形分割为直角三角形再进行求解．但是怎么添高大可斟酌．

确定性思想 已知角 高

解三角形的前提是有直角三角形，如果是在锐角三角形和钝角三角形中，就需要通过作辅助线的方法构造直角三角形来求解．解三角形时作辅助线的常用方法是添加三角形的高，但是怎么添高却大可斟酌．

解三角形首先要确定一个思想：当一个三角形有三个独立的条件时，此三角形就唯一确定，即满足：①已知三条边(边边边)；②已知两边及其夹角(边角边)；③已知两角及一边(角角边或角边角)．需注意的是，如果已知三角形的三个角，那么该三角形不是唯一确定的，因为第三个角可以由其他两角推导出来，也就是说它们是不独立的．以上所说的已知角可以是已知角度，也可以是已知角的三角函数值．

当一个三角形符合以上三种情况之一时，该三角形的其他要素也就唯一确定，原则上都可以通过计算求得．

例1 在△ABC中:

(1)当∠A=30°，∠B=45°，AB=2时，求AC，BC；

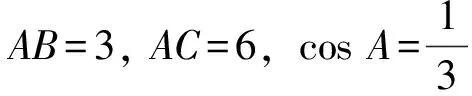
(3)当AB=4，BC=5,AC=6时，求cosA，S△ABC．

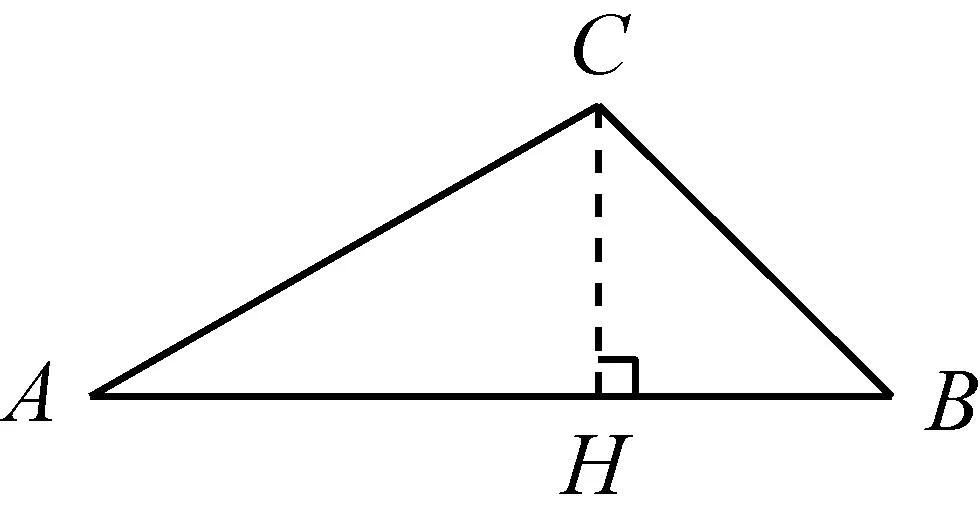
图1

解：(1)如图1，作CH⊥AB．

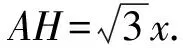
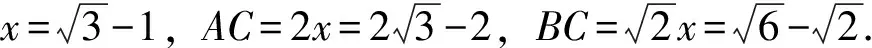
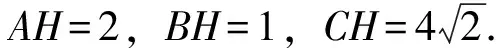
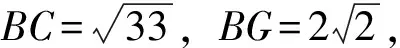
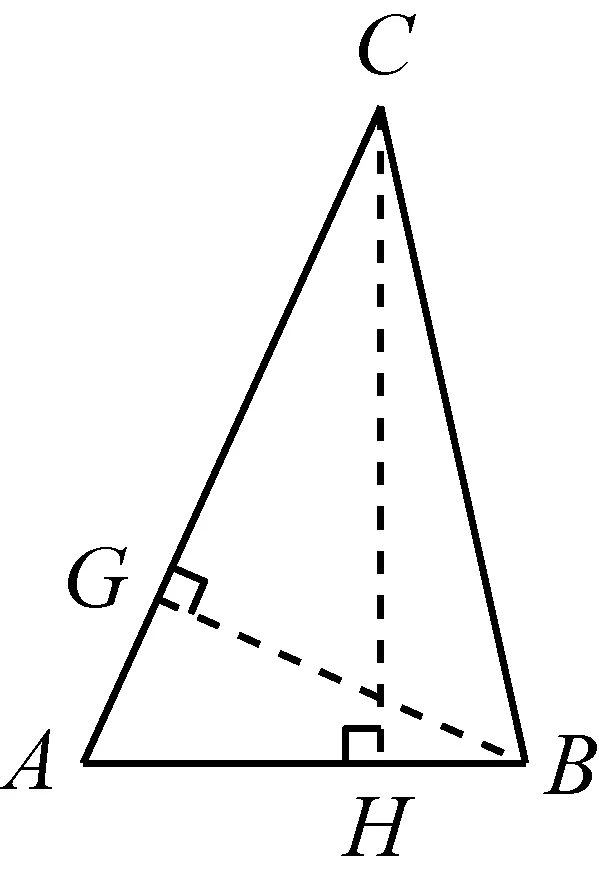
图2

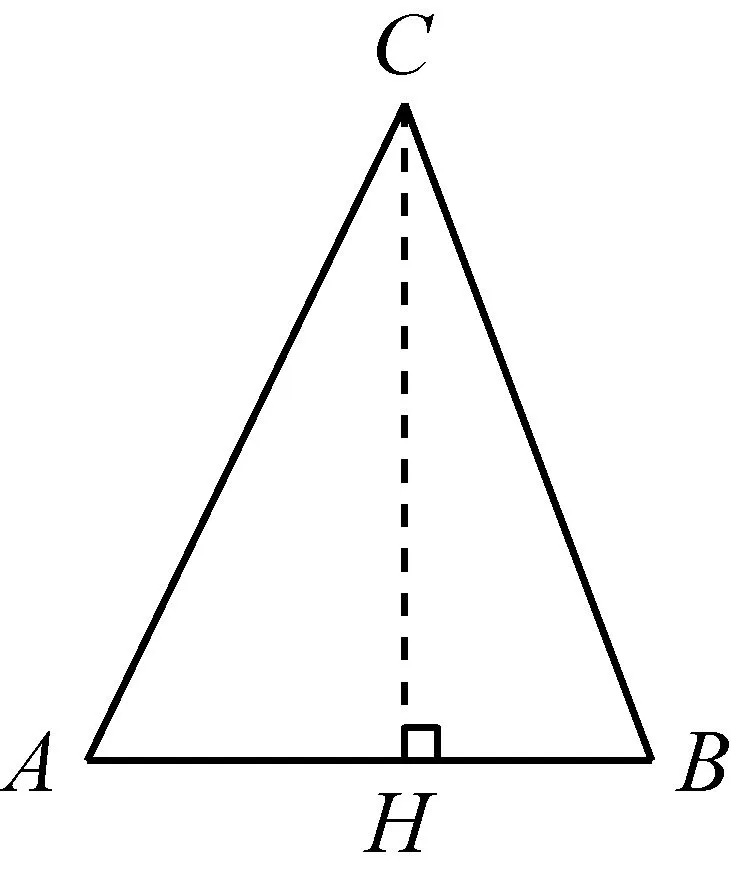
图3

(3)如图3，作CH⊥AB．

根据题意, 设AH=x,BH=4-x．

根据勾股定理有CH2=AC2-AH2=BC2-BH2,

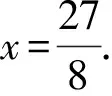
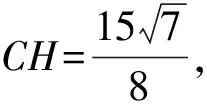
本题的三个小问分别对应角边角、边角边、边边边型三角形．应让学生熟练掌握这些三角形的解法，也就是通过添加高线将原三角形分割成直角三角形来求解．

确定了解三角形的指导思想后，还需掌握添加高线的一个技巧，即添已知角所对的高(或垂线)．

例2 已知B港口位于A观测点北偏东53.2°方向，且其到A观测点正北方向的距离BD的长为16 km．一艘货轮从B港口以40 km/h的速度沿如图4所示的BC方向航行，15 min后到达C处．现测得C处位于A观测点北偏东79.8°方向．求此时货轮与A观测点之间的距离AC的长(精确到0.1 km)．

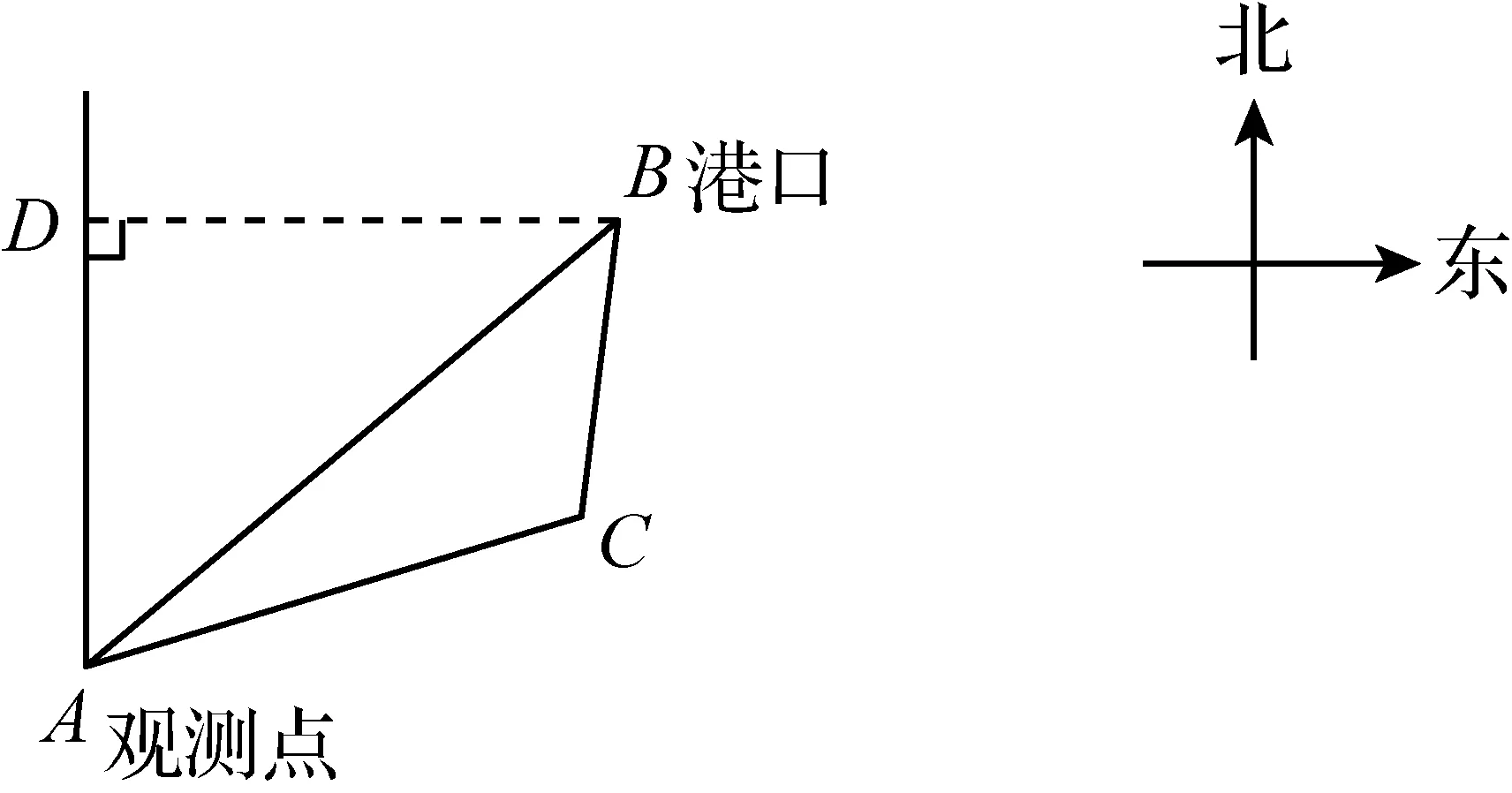
图4

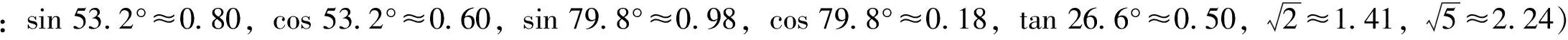
分析：在△ABC中，容易得出AB=20，BC=10，∠BAC=26.6°．本题的实质就是在已知三角形的两边和一边所对角的条件下，求第三边AC的长．

解：(方法1)如图5，过点C作CE⊥AB于点E．

由题意得∠DAB=53.2°，∠ABC=45°，∠DAC=79.8°，BD=16 km．

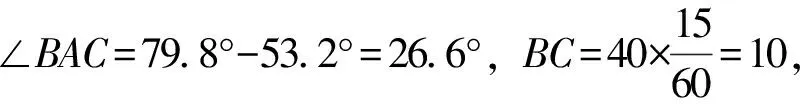
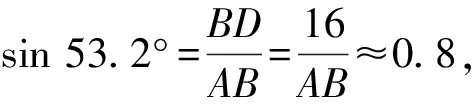
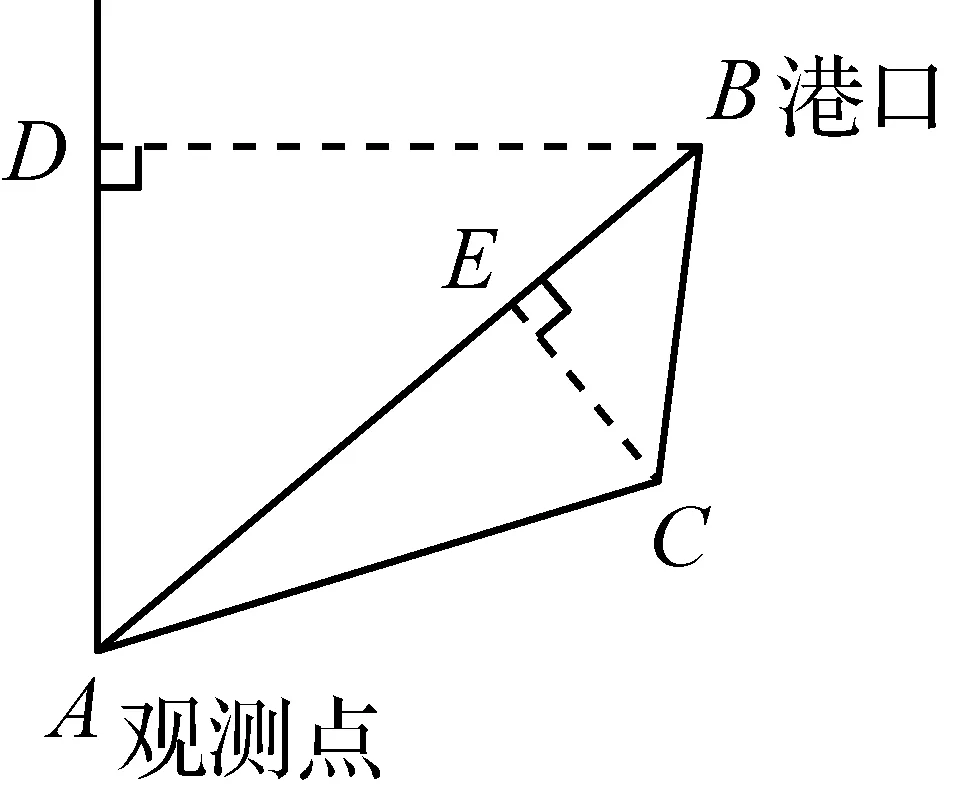
图5

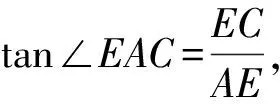
在Rt△BEC中，BE2+CE2=BC2,即(20-2EC)2+EC2=102，解得EC=6或EC=10．

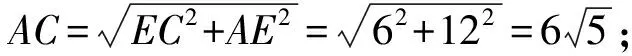
当EC=10时，EA=20，不符合题意，舍去．

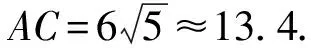
答：此时货轮与A观测点之间的距离AC约为13.4 km．

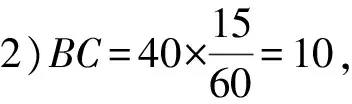
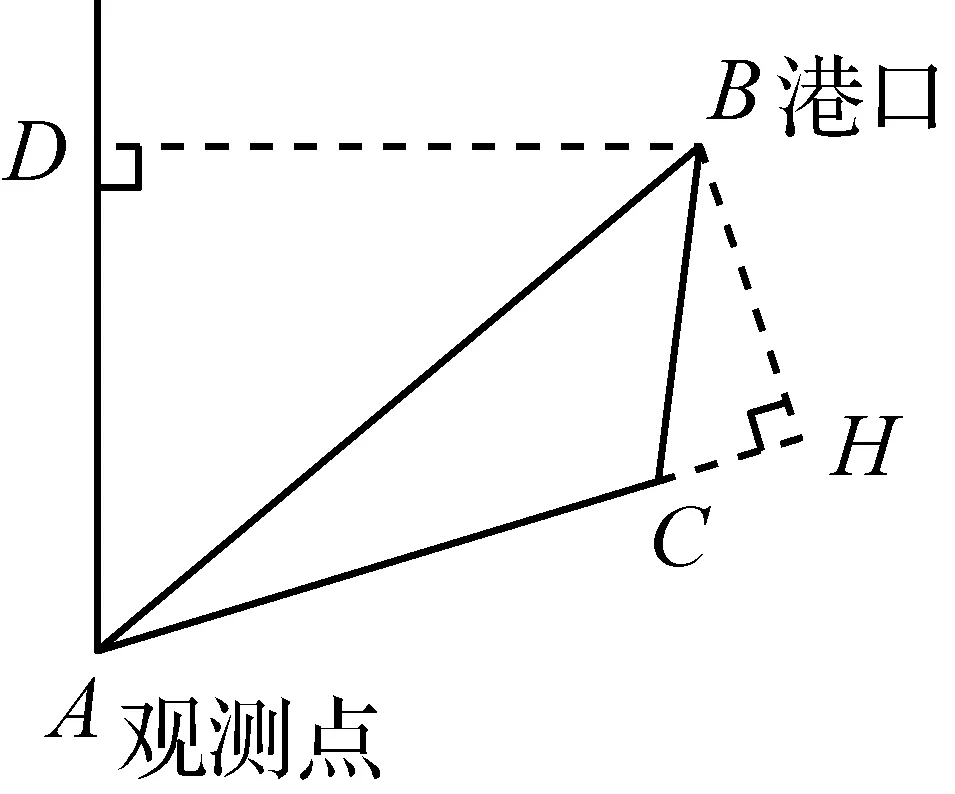
图6

如图6，过点B作BH⊥AC,交AC的延长线于点H．

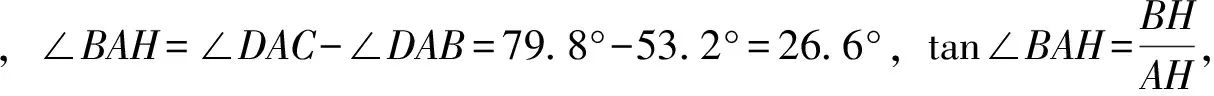
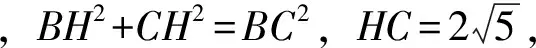
答: 此时货轮与A观测点之间的距离AC约为13.4 km．

【点评】方法1和方法2都是通过添∠BAC所对的高来解本题的(因为已知tan 26.6°≈0.50)．那么是否可以过点A作BC的高AF？实际上，若通过点A作BC的高AF，就构造了Rt△AFC和Rt△AFB,如果设FC=x或AF=x，都难以利用∠BAC=26.6°这个条件．

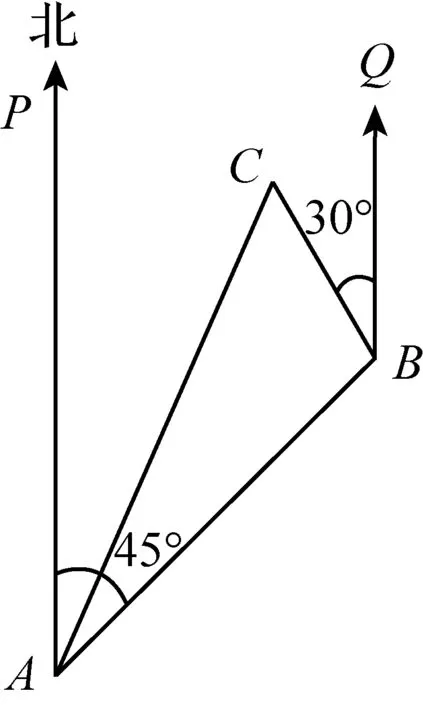
图7

例3 如图7，一条小船从港口A出发，沿北偏东45°方向航行20海里后到达B处，然后又沿北偏西30°方向航行10海里后到达C处，问：此时小船距港口A多少海里？

解：(方法1)如图8，过B点作BE⊥AP，垂足为点E；过C点作CD⊥AP，垂足为点D，延长DC交BQ于点F． 易知四边形EBFD为矩形，DF=BE,DE=BF．

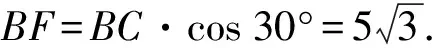
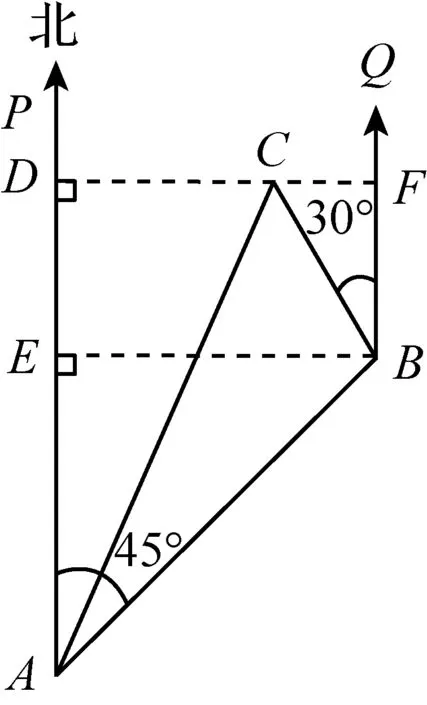
图8

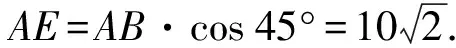
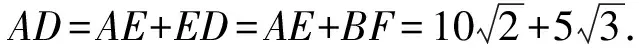
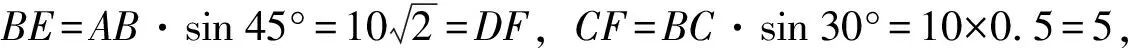
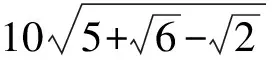
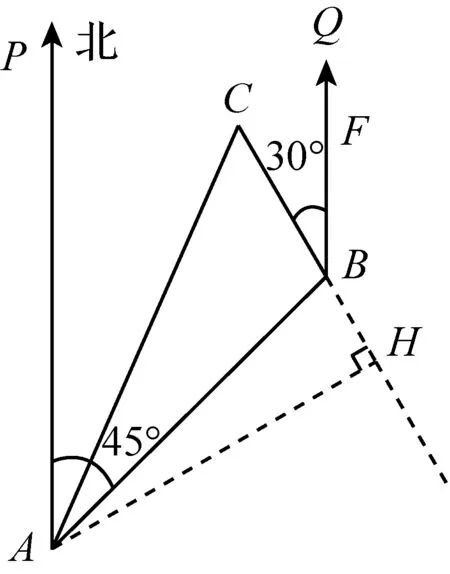
图9

(方法2)如图9，作AH⊥CB,垂足为H，易得∠ABH=75°．

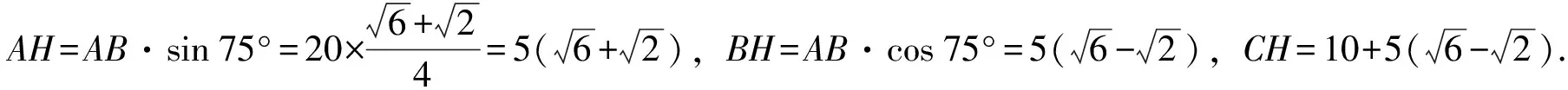
【点评】方法1和方法2有什么区别？方法1所用为初中教学要求的特殊角运算，而方法2用到了75°角，但对于初中生来说，教材不作记忆要求，因此这个75°角的条件难以利用．

最后，注意一个细节：当已知角是钝角时，不能作钝角所对的高．可把该钝角切割，或找该角的邻补角(即外角)所对的高．

如对于例3，可换个思路，把钝角切割．

(方法3)如图10，过点B作BE⊥AP，垂足为点E；过点C分别作CD⊥AP，CF⊥BE，垂足分别为点D，F． 易知四边形CDEF为矩形，CD=EF,DE=CF．

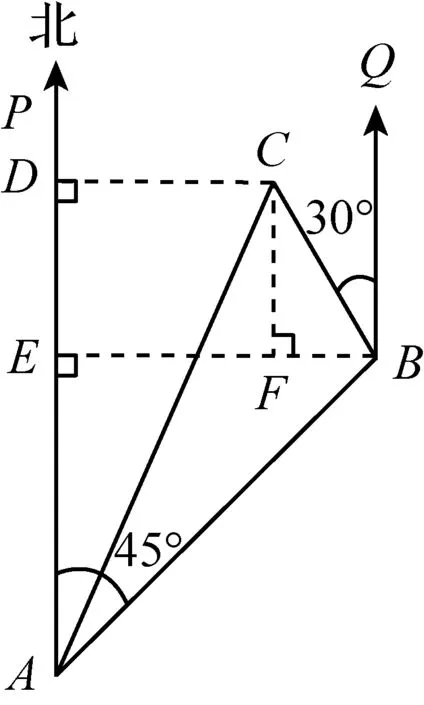
图10

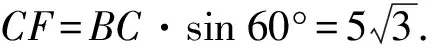
在Rt△ABE中，

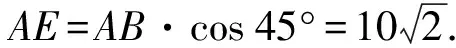
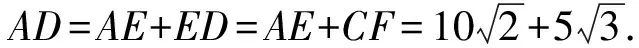
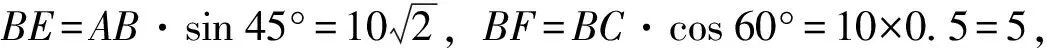
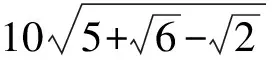
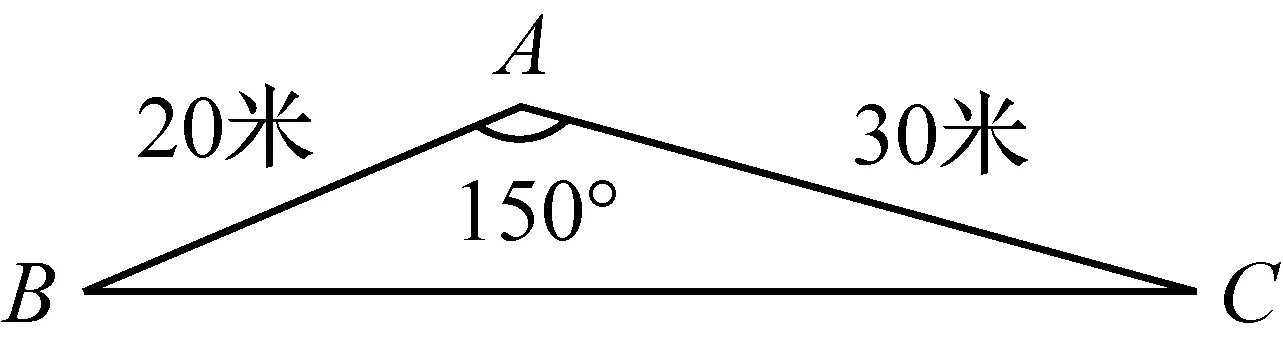
图11

例4 某市在旧城改造中，计划在市内一块如图11所示三角形空地上种植草皮以美化环境，已知这种草皮每平方米售价a元，则购买这种草皮至少需要( )．

A.450a元B.225a元C.150a元D.300a元

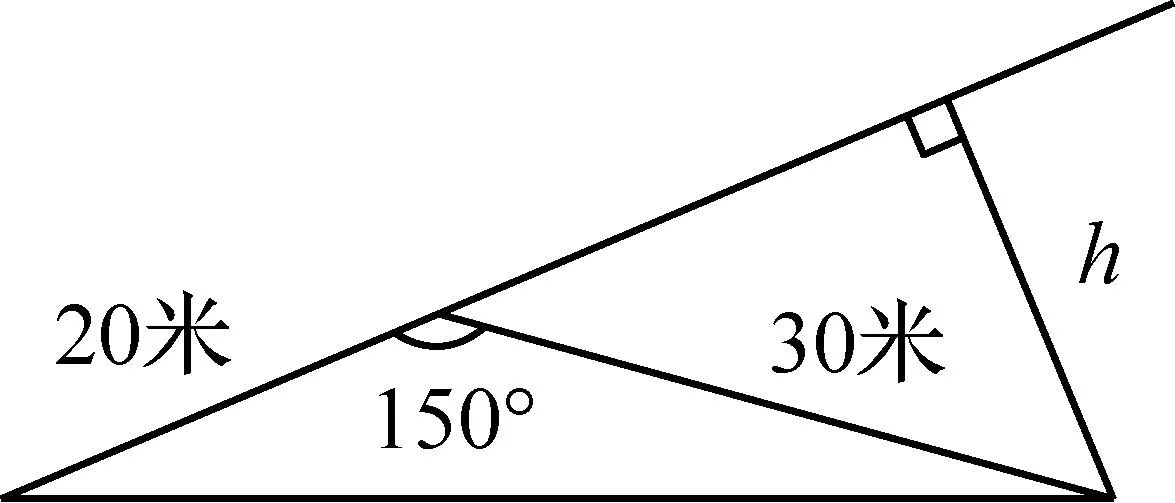
图12

【点评】这道题的背景对学生来说熟悉而又简单，但本题有较高的区分度，主要是因为已知的150°角无法切割．如图12，要先求出150°的外角为30°，再作出20米边上的高，根据含30°角所在直角三角形的性质即可求出高，从而得到面积，再根据这种草皮每平方米a元即可求得结果为150a元．答案选C．

解直角三角形是初中数学的重要内容之一，利用解直角三角形的方法来解决一般三角形问题，是初中生数学学习的难点之一，也是近几年中考的热点问题．在解答与之相关的问题时， 除了必须掌握直角三角形的边角关系外，还要灵活运用一些重要的数学思想与方法，善于在复杂的图形中找到一个确定的一般三角形．利用添加已知角所对高的办法添加辅助线，构造直角三角形．因此我们教师在平时的教学中，不管题目的难度如何变化，背景如何翻新，万变不离其宗，教会学生掌握了这个方法，也就等于掌握了解直角三角形的有力工具！

[1]陈永明．陈永明讲评数学题[M]．上海：上海科技教育出版社, 2013．

(责任编辑：李 佳)

① 本文系广东省教育科学规划课题《渗透数学的真善美，提升初中数学教育的价值》的研究成果(课题批准号2016YQJK168).