一道高中数学期中试题的命制心路及感想①

梁淮森



一道高中数学期中试题的命制心路及感想①

梁淮森

(福建省南安第一中学，南安 362300)

本文通过对一道高考真题多角度、多层次的改编，深入剖析试题的命制意图，完整呈现了一道高三期中立体几何解答题的命题过程，并给出了实测追踪及考后反思，体现出教师在立体几何教学中，深入研究高考真题，把握问题本质，渗透优化决策思想，引导学生化繁为简的必要性．

试题 设计意图 几何法 坐标法 优化决策

立体几何在高考中占据重要的地位，每年高考均有一道解答题，多以棱柱、棱锥和棱台为载体，主要考查线面、面面位置关系的证明及线线、线面和面面夹角的求解．从2001年新课程改革开始，由于理科数学增加了空间向量这个“杀手锏”，立体几何问题似乎一下子由较难问题变为中档偏易问题．然而近几年立体几何问题命题趋向于综合考查学生的空间想象能力、代数方程思想、平面解析几何或向量的方法等．考题虽然仍以空间直角坐标系为主要的解题工具，但建系不再那么一目了然，对空间想象能力的要求大大提高，经常出现对过去传统的题进行视角变换或将基本图形的元素进行增、减等变化．很多学生遇到这类题型往往会感到不习惯，从而导致整体得分率较低．

由于空间直角坐标系的应用，理科学生解立体几何问题一般都用坐标法解决，教学中也较少介绍几何法解题方法(一般只涉及证明平行或垂直)，因此用几何法思考对学生来说是一大困难．在学校高三上学期期中学情调查考试中，笔者命制了高三理科数学试卷，命题按照全国高考考试说明对相关内容的要求，试卷样式同高考全国卷一致．根据命题的构想要求，想要编一道不易建立空间直角坐标系的立体几何解答题．为了设置建系难点，以几何法解题背景下的考题进行改编命制．在试题命制过程中，感触颇深，下面谈一谈此题的命制意图、命制过程与感想，希望与同行交流探讨．

一、试题内容

1.试题展示

如图1，三棱柱ABC-A1B1C1中，D,M分别为CC1和A1B的中点，A1D⊥CC1，侧面ABB1A1为菱形，且∠BAA1=60°，AA1=A1D=2，BC=1．

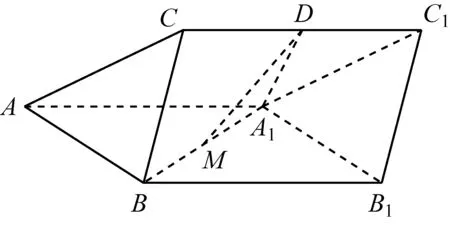
图1

(Ⅰ)证明：直线MD∥平面ABC；

(Ⅱ)求二面角B-AC-A1的余弦值．

2.试题解答

第(Ⅰ)小题的几何法解题过程略，下面展示坐标法简要解析．

(方法1)由勾股定理，易得CB⊥BA,CB⊥BA1，

所以CB⊥平面ABB1A1．

如图2，取AA1中点F，以点B为原点，以BB1，BF,BC为x,y,z轴建立直角坐标系．

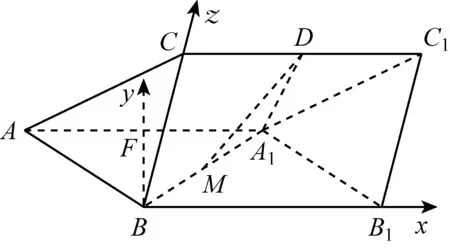
图2

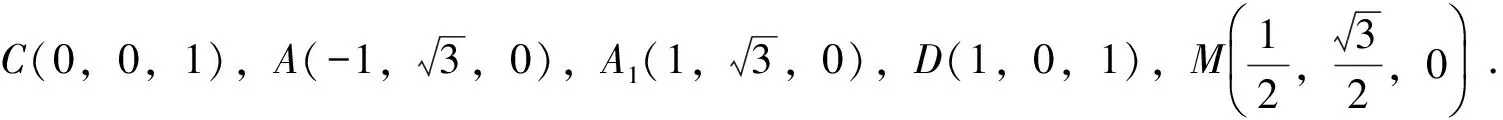
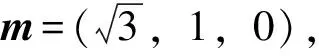
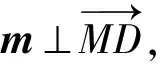
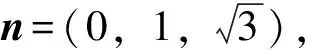
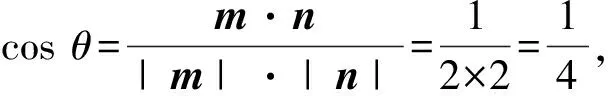
(方法2)如图3，以B为原点，以BB1,BF分别为x,y轴建立空间直角坐标系，设点C(a,b,c)．

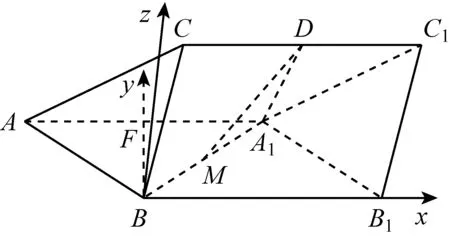
图3

A,B,B1,A1,M各点的坐标同方法1，

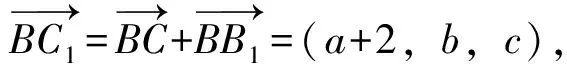
C1(a+2,b,c)，所以D(a+1,b,c)．

由A1D⊥CC1，A1D=2，BC=1，

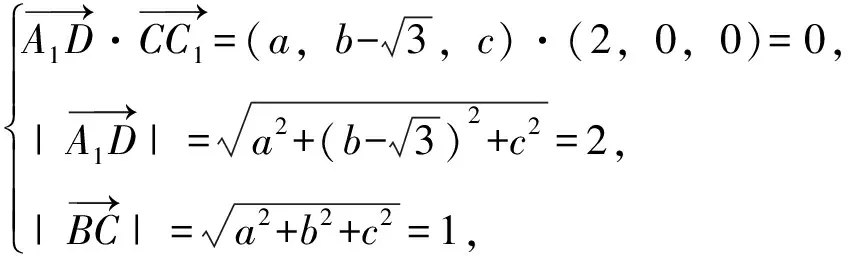
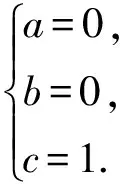
所以C(0,0,1)，C1(2,0,1)，D(1,0,1)，下同方法1．

二、命制过程

为了设置建系难点，需考虑寻找几何法解题背景下的考题． 通过对近几年高考试卷中立体几何解答题的研究与分析，最终决定以2011年全国卷大纲版第19题为原型进行改编．

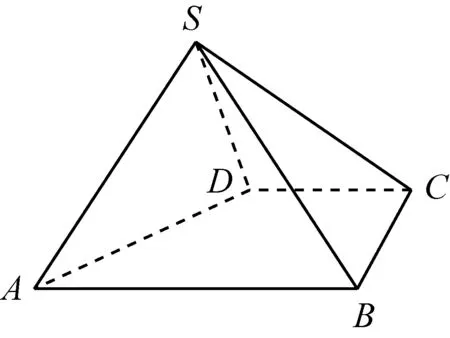
图4

原题：如图4，四棱锥S-ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形，AB=BC=2，CD=SD=1．

(Ⅰ)证明：SD⊥平面SAB；

(Ⅱ)求AB与平面SBC所成角的大小．

1.设置建系难点，规避直角坐标系

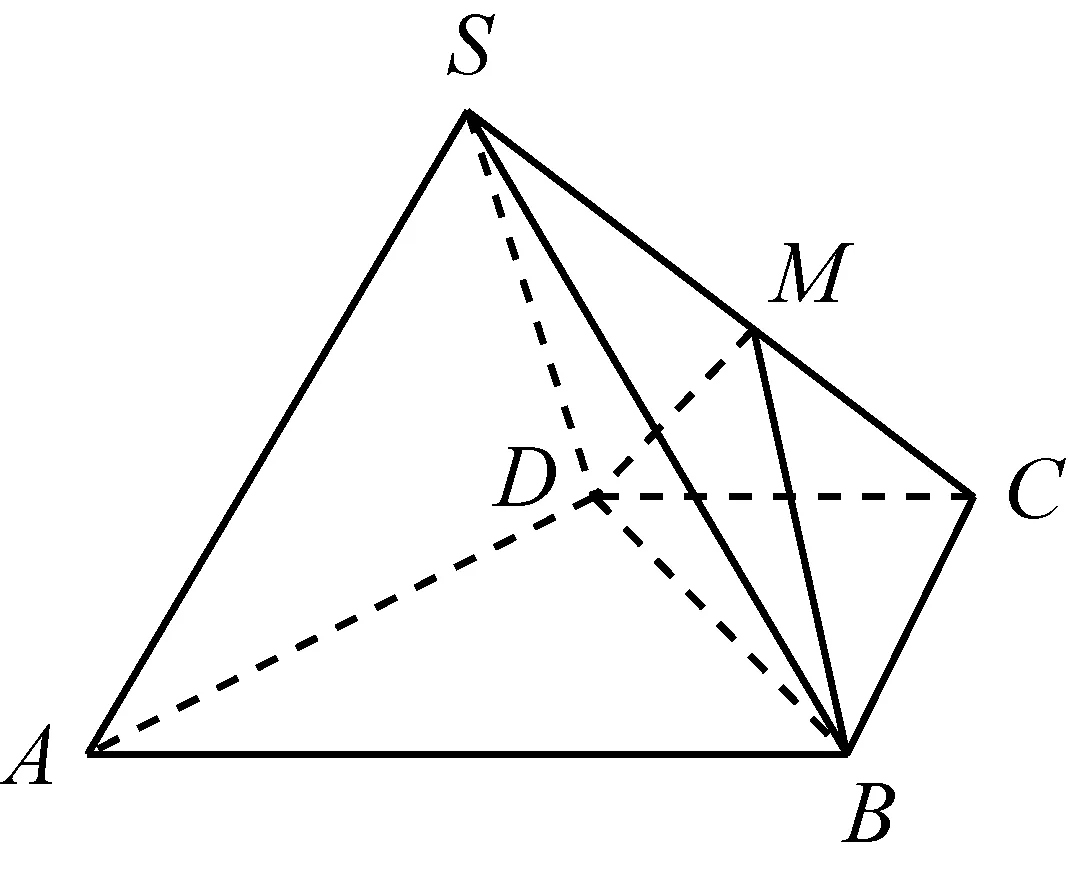
图5

题目1 如图5，四棱锥S-ABCD中，AB∥CD,BC⊥CD，侧面SAB为等边三角形，AB=BC=2，CD=SD=1．

(Ⅰ)证明：SD⊥平面SAB；

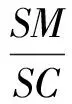
【设计意图】针对原题建系难的特点，意图考查纯几何法解题．考虑到教学较少涉及空间角的几何法求解，因此设计第(Ⅱ)小题考查直线与平面平行的判定及性质、平面几何知识的应用等知识，考查转化与化归、函数与方程等思想方法；考查学生的空间想象能力、推理论证能力、运算求解能力等．

2.变换图形结构，力求一题多解

考虑到几何体中存在线面垂直关系，把几何体旋转一个角度，有利于建立坐标系解题，使得题目解法多样化．

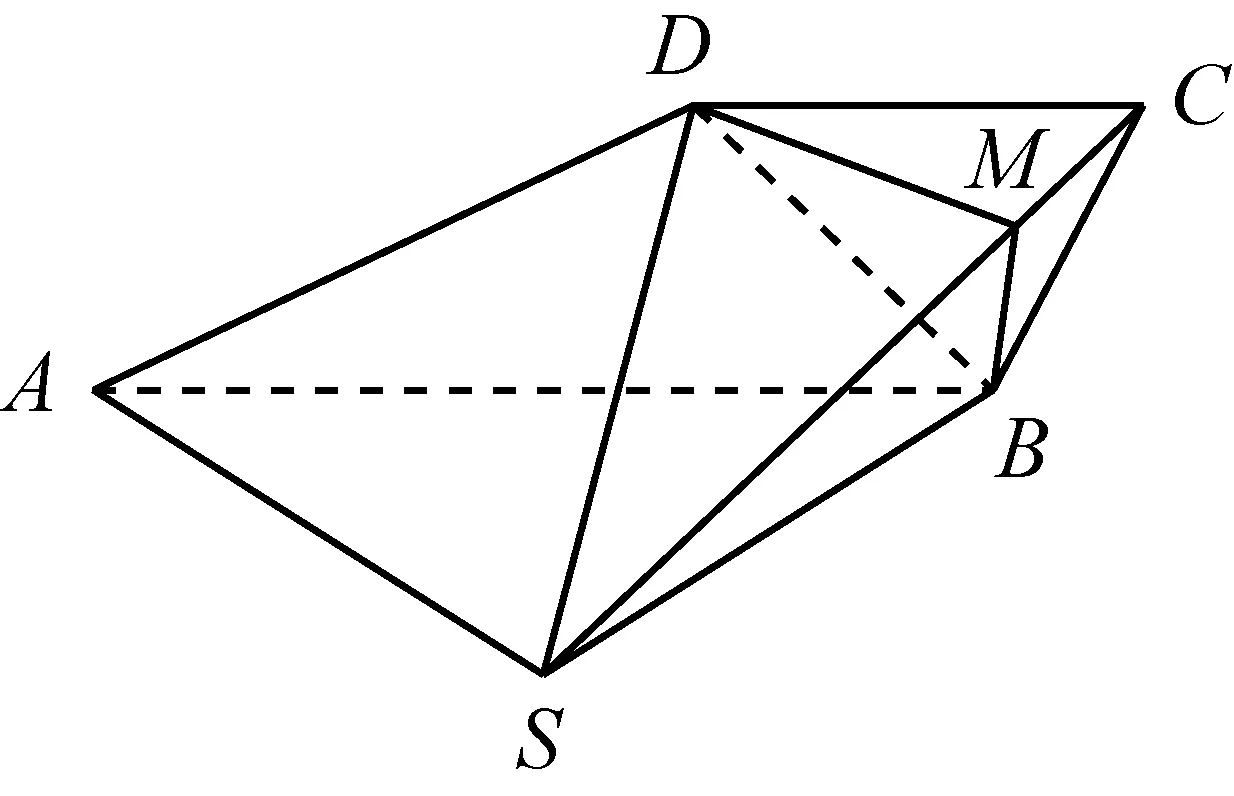
图6

题目2 如图6，四棱锥S-ABCD中，AB∥CD,BC⊥CD，侧面SAB为等边三角形，AB=BC=2，CD=SD=1．

(Ⅰ)证明：SD⊥平面SAB；

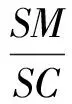
【设计意图】变换图形方位，引导学生利用第(Ⅰ)小题的结论建立空间直角坐标系，利用坐标法解决探索性问题(Ⅱ)．同时，纯几何法解本题仍然适用，使得解题多样化．

3.变换题目设问，改变考查重点

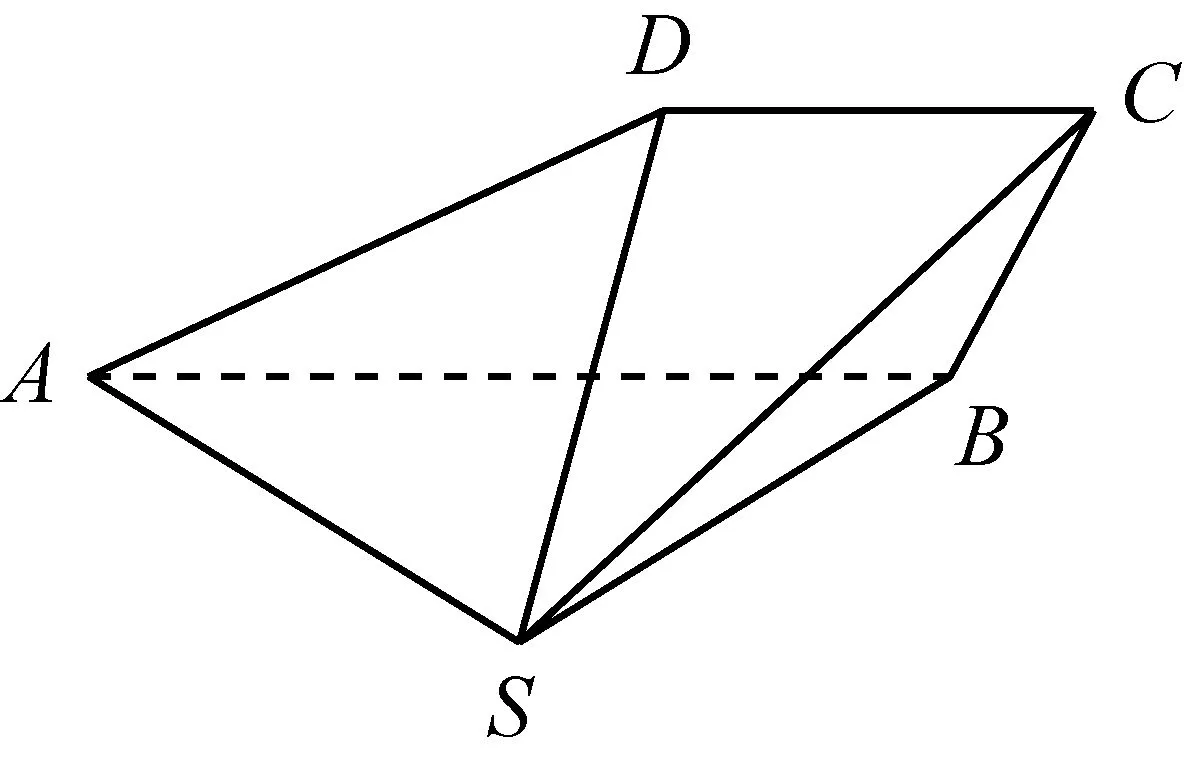
图7

由于空间角问题是立体几何中的一大重点，题目2经改变图形结构，建立坐标系不再是难点，可考查空间角问题．此外，综合全国卷命题特点，其命题语言均简洁明了，甚少考查这类探索性问题，因此考虑把第(Ⅱ)小题改换为原题的线面角问题．

题目3 如图7，四棱锥S-ABCD中，AB∥CD,BC⊥CD，侧面SAB为等边三角形，AB=BC=2，CD=SD=1．

(Ⅰ)证明：SD⊥平面SAB；

(Ⅱ)求AB与平面SBC所成角的大小．

【设计意图】题目语言、图形简洁明了，考查直线与平面垂直、直线与平面所成的角及平面几何知识的应用；考查空间向量在立体几何中的应用．

4.再设建系难点，直面直角坐标系

题目3的设计已经完全偏离了最初想要编一道不易建立空间直角坐标系的立体几何解答题的构想．由于第(Ⅰ)小题的引导作用，在题目3中建立直角坐标系变得简单易行，因此决定去掉第(Ⅰ)小题的引导作用，改成平行问题．

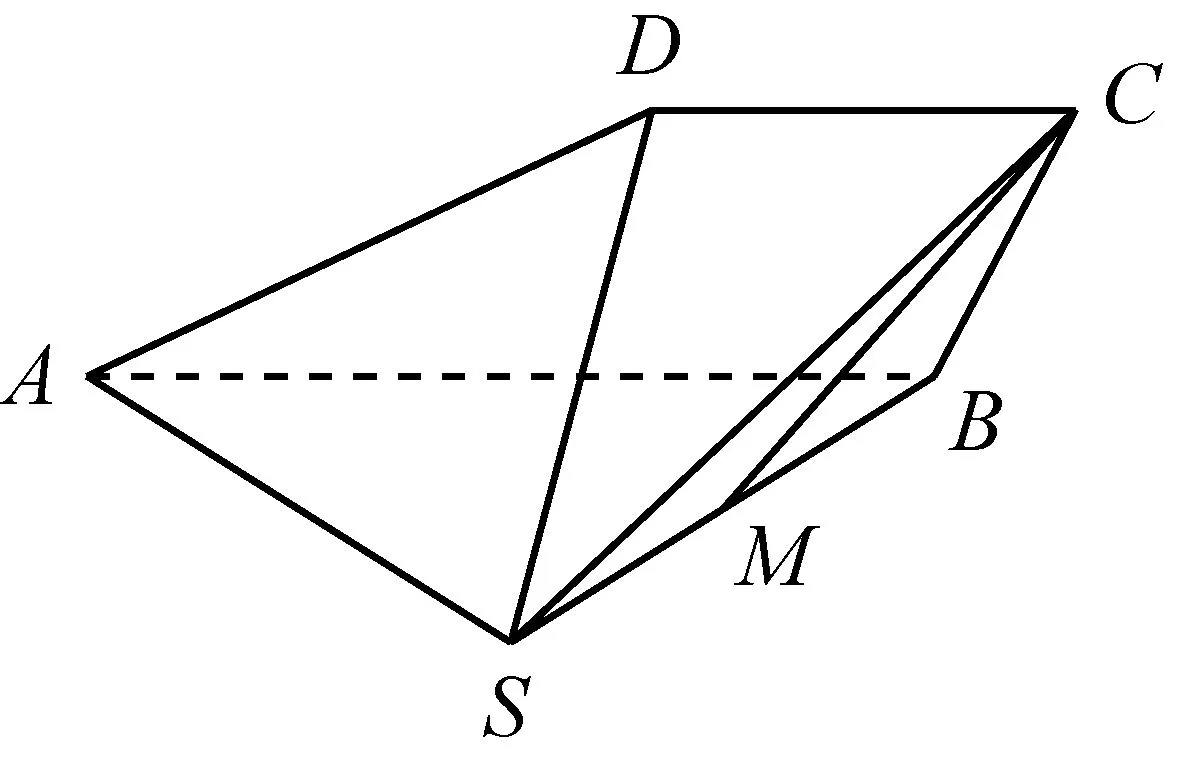
图8

题目4 如图8，四棱锥S-ABCD中，AB∥CD,BC⊥CD，侧面SAB为等边三角形，AB=BC=2，CD=SD=1，M为SB的中点．

(Ⅰ)证明：MC∥平面SAD；

(Ⅱ) 求AB与平面SBC所成角的大小．

【设计意图】加大难度，考查直线与平面平行、直线与平面垂直及直线与平面所成的角等知识；考查转化与化归思想；考查空间想象能力、推理论证能力、运算求解能力等；此外，还考查了学生合理猜想、严格证明的数学思想方法．

5.再变图形设问，完善考查方位

近几年来的全国卷立体几何命题常以菱形为底面，考虑到这一命题特点，把题目4的四棱锥扩充成三棱柱．并且希望第(Ⅰ)小题与第(Ⅱ)小题有关联，因此对(Ⅱ)小题再作修改．

题目5(定稿) 如图9，三棱柱ABC-A1B1C1中，D,M分别为CC1和A1B的中点，A1D⊥CC1，侧面ABB1A1为菱形，且∠BAA1=60°，AA1=A1D=2，BC=1．

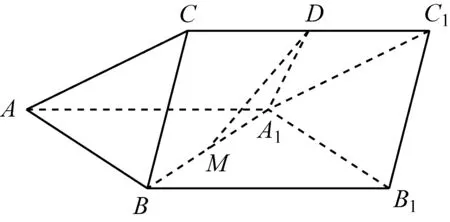
图9

(Ⅰ)证明：直线MD∥平面ABC；

(Ⅱ)求二面角B-AC-A1的余弦值．

【设计意图】以横放的斜三棱柱为载体，考查三棱柱的特征，空间点、线、面的位置关系，平面几何知识的应用，空间向量的运算及应用等知识，实现对转化与化归思想、空间想象能力、逻辑推理能力及运算能力的考查．并要求学生能够合理猜想、严格证明，综合性较强，难度较大．

三、命题感想

1.试题特点

试题第(Ⅰ)小题可以用几何法证明，且难度不大，对于不能建立坐标系的学生不致全军覆没，且第(Ⅰ)小题既可以直接证明线面平行，也可以通过构造平面，证明面面平行以得到线面平行，具有一定的灵活机动性．

试题第(Ⅱ)小题用几何法解题较难，适宜于建立坐标系解题．根据棱长数据易得BC⊥BA，可合理猜想BC⊥平面ABB1A1并证明，从而建立直角坐标系；也可以在平面ABB1A1选择好x,y轴，建立未知z轴的坐标系，并设点C的坐标为(a,b,c)，利用坐标诠释题干条件，先列方程解出a,b,c的值再求解．两种解法分别考查了空间想象能力及转化与化归思想，具有一定的难度．

而试题第(Ⅱ)小题所求二面角的一个半平面ABC和第一步所证平面一样．对于能够建立坐标系的学生，可选择用坐标法利用法向量证明线面平行，其法向量在第二步可重复使用，降低了运算量，是一种更优化的选择，可以体现学生在审题中的观察能力及优化决策思想．

2.实测追踪

本校有484名高三理科学生参加考试，第(Ⅰ)小题做对者473人，正确率高达97.7%，其中使用坐标法解题者只有1人．第(Ⅱ)小题能建立正确坐标系的学生不到100人，正确率低至20%，其中以BA,BC为坐标轴建立坐标系者共2人．

本题的几何体以菱形为底面，学生遇到底面为菱形的几何体时，经常以菱形的中心为原点建立直角坐标系．受这一思维定式影响，本题在实测考查中，很多学生仍然希望以菱形中心M为原点建立坐标系，因此出现很多学生以MC为z轴的错误猜想．而方法2由于教学当中基本没有涉及，学生都不懂得应用．因此学生在第(Ⅱ)小题中几乎“全军覆没”．

另外，学生对第(Ⅰ)小题的证明大多会使用几何法证明，能建立直角坐标系的学生也很少会注意观察到两个小题中使用到同一个平面，从而做出选择利用法向量证明线面平行的优化决策．事实上，如果在建立直角坐标系的时候选择以BA,BC为坐标轴，则平面ABC为坐标平面，其法向量不用求，又降低了不少的运算量．在教学中，应注意渗透此类优化决策思想的应用，帮助学生提高解题效率．

3.考后反思

本题的难点在于建立空间直角坐标系，为埋伏铺垫、设置梯度，可加入一个小题：“求证：BC⊥BA1．”这一小题有利于引导学生更加容易猜想到BC⊥平面ABB1A1，使题目难度下降，且变化之后的考点与原题相同．

本题在实测考查当中第(Ⅱ)小题的得分率非常低，这提醒了我们考虑教学是否应适当注意这种不易建立直角坐标系的问题的处理方法．而本题方法2为我们提供了一个不错的选择，通过建立“半个直角坐标系”，把空间想象和几何证明的难度转化为空间坐标的运算，充分体现了坐标法的优点．并且这种方法也是一个较为普适性的解题通法，值得我们推广应用．

四、结语

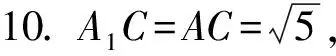
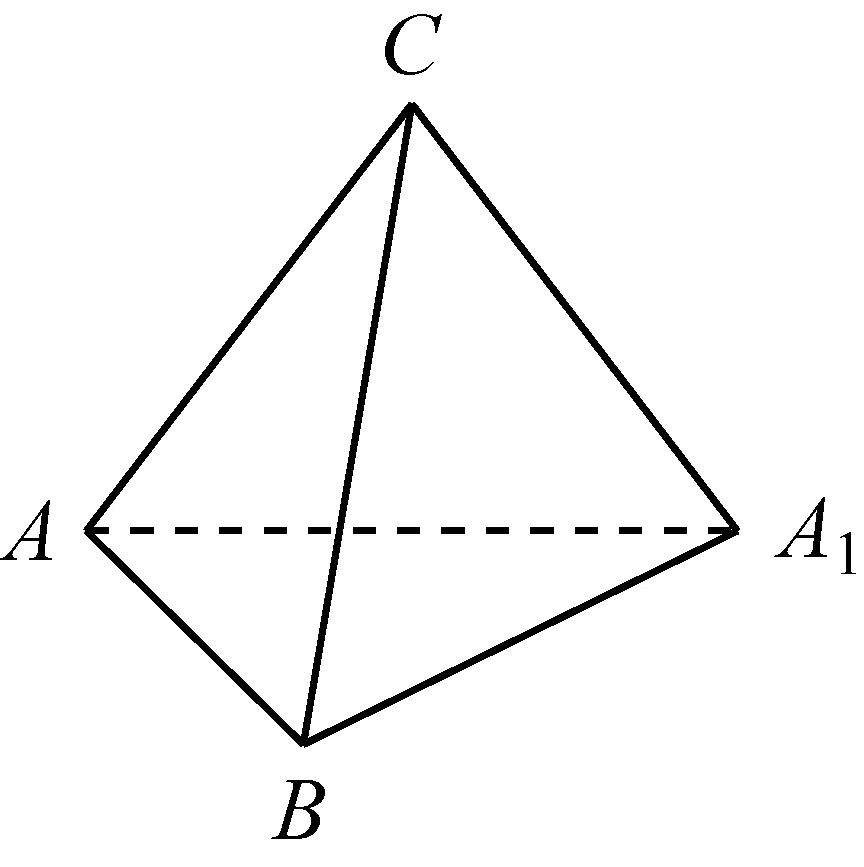
图10

BC=1,AB=BA1=2，在这个主干图形中易得BC⊥平面ABA1，而将基本图形的元素进行增加变换后，以上线段长度信息变得隐蔽，线面垂直关系的发现变得困难．因此，在高三立体几何的教学和复习中，教师要认真研究历年高考试题，吃透问题的本质，有意识地对学生熟悉的图形进行图形元素的增、减变换，并教会学生将图形化繁为简的方法，在错综复杂的条件信息中提炼出基本图形，注重引导学生进行一题多解，以培养学生的创新能力．

[1]黄晓琳，姚承佳．一道质检题的命制过程与反思[J]． 中学数学教学参考，2013(9)：48-51．

[2]佟成军，黄明明．一次命题及考后的点滴记录和思考[J]． 中学数学教学参考，2014(1-2)：135-137．

[3]扬苍洲，姚承佳．一道试题的命制思路[J]． 数学教学，2011(11)：35-36，38．

[4]陈云平．高中数学试题命制的实践与认识[J]． 数学通讯，2012(5)：52-56．

(责任编辑：李 佳)

① 本文系2015年福建省基础教育课程教学研究立项课题《高中数学作业(含试卷)有效设计与讲评实证研究》(立项批准号MJYKT2015—069)部分研究成果．