三谐振弹性波超材料的带隙研究

杨厚禄， 王公正， 莫润阳， 宿贵梅， 胡　静

(陕西师范大学 物理学与信息技术学院， 陕西 西安 710119)



三谐振弹性波超材料的带隙研究

杨厚禄， 王公正*， 莫润阳， 宿贵梅， 胡静

(陕西师范大学 物理学与信息技术学院， 陕西 西安 710119)

摘要：基于集中参数模型动力学法，研究了具有三谐振系统弹性波超材料能带结构、数值模拟参数对有效质量及能带结构的影响。理论及仿真研究表明，有效质量具有频率依赖性，在3个频率位置处的有效质量为负值，频率位置和带宽可由模型参数调节；材料存在3个带隙，增加内部谐振子弹性系数可将带隙向高频移动，同时有拓宽带隙作用。通过增加谐振子质量可使带隙向低频移动，选择适当参量可设计低频宽带弹性波超材料。

关键词:弹性波；超材料；负有效质量；带隙

PACS: 43.38.+n

超材料(Metamaterials)指具有自然界材料所不具备特殊属性的人造微结构复合材料，最初被发现和用于调制电磁波[1-4]。由于具有负有效参数特性(如负磁导率、负介电常数等)，超材料可表现一些新奇现象，如负折射率、反常多普勒效应、左手现象等。典型超材料光子(声子)晶体是一种新型复合结构[5-6]，其介电常数(弹性常数)随空间周期性变化。当电磁波与周期排列的介电材料相互作用时受到调制形成带隙，使一定频率范围的电磁波无法传播。由于电磁波在光子晶体中传播与弹性波(如声波)在声子晶体中传播有相似之处，弹性波超材料在声学等领域受到关注[7-22]，实际应用有声滤波器、声波导管、噪声与振动控制等方面[7-13]。

弹性波超材料结构尺度属于亚波长尺度范围，材料结构尺寸远小于其对应的工作波长，波对材料的结构特征无法感知，因此可近似看成均匀介质并用有效参数描述，如有效质量密度、有效模量等[14-18]。最近，不同微结构弹性波超材料被设计出以实现负有效参数，Wang实现了有效弹性模量和有效质量的独立控制[17]，Huang设计了含内质量单元的晶格系统[18]，Liu研究了单负属性的宽带弹性波超材料[19]，此材料只有两个阻带，其中第二个阻带理论上无限宽，第一个阻带的起始频在5 000 Hz以上。

现有的超材料对低频波的处理(如水下低频波吸收，空气中小于400 Hz噪音处理等)有困难，并且在某些弹性波器件的应用中可能需要多带隙弹性波超材料。为了得到能带结构丰富的低频宽带弹性波超材料，本文设计了三谐振系统，利用集中参数模型动力学分析方法展示了有效质量的频率依赖性；用有效质量代替原子质量，用线性弹簧代替原子间的恢复力常量，将固体理论[23]中一维单原子链模型转换成周期质量-弹簧晶格系统，数值模拟了弹性波在系统中的传播，通过调节参数对带隙进行设计，使能带结构更加丰富。

1模型及计算理论

1.1三谐振质量-弹簧模型及有效质量

设计了一个三谐振质量-弹簧微结构模型，如图1所示，由三组弹簧三层质量壳和一个中心质量球组成。中心质量球的质量为m1，与其相邻由内而外壳层质量分别为m2、m3和m4，弹性系数分别为k1、k2和k3的线性弹簧把它们依次连接成三谐振系统。设中心谐振子及由内而外相邻各质量壳的位移分别为u1、u2、u3、u4，则系统的动力学方程为

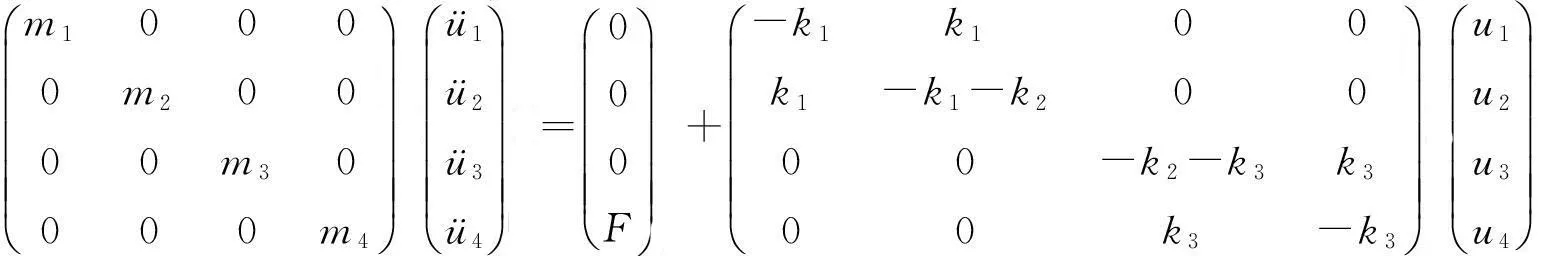
(1)

设外部简谐激励和系统响应位移分别为:

F(t)=F0e-iωt,

(2)

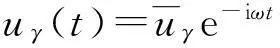
(3)

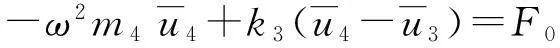
(4)

根据牛顿第二定律定义有效质量meff，由(4)式得

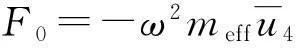
(5)

则三谐振系统有效质量为

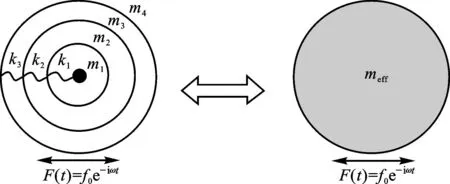
图1　三谐振质量-弹簧微结构系统及其有效质量

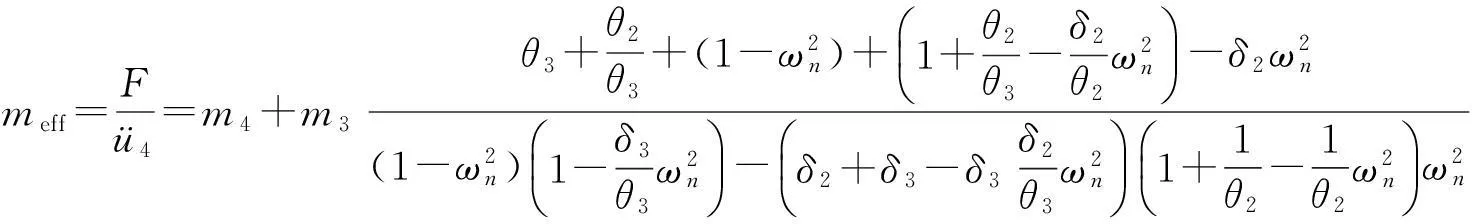
(6)

(7)

则归一化有效质量为

(8)

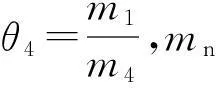
1.2无限周期晶格系统能带计算理论

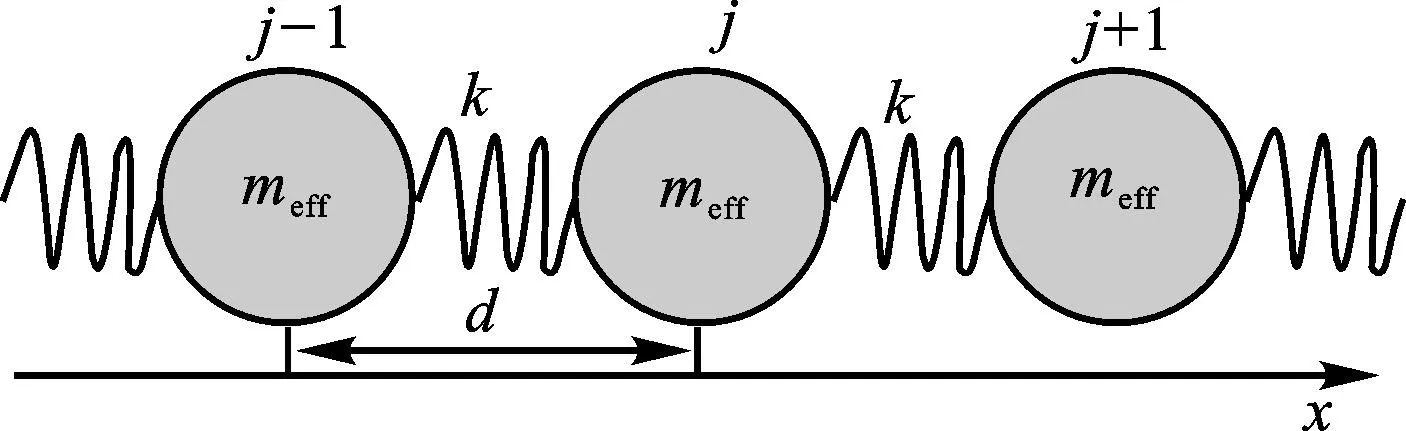
图2　无限周期质量-弹簧晶格系统

根据Bloch定理，在周期边界条件下第j+n个格点的振动位移有以下形式

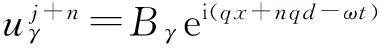
(13)

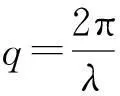
将(13)式分别带入(9)—(12)式可得

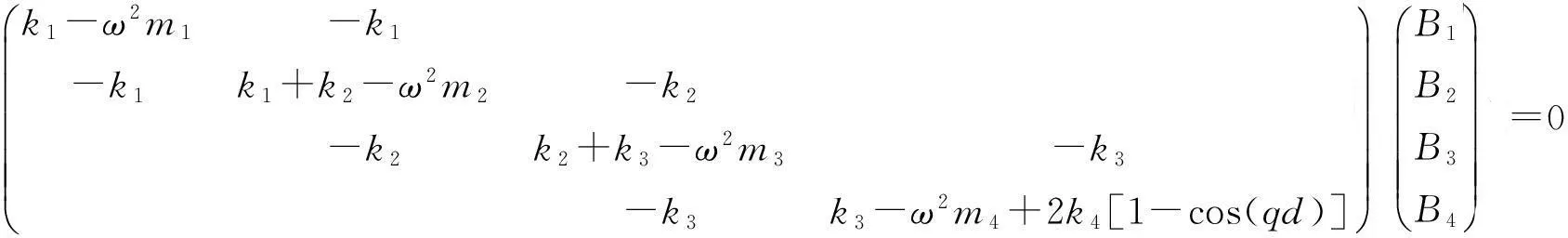
(14)

要使以上方程有非零解，则系数行列式必为零，即

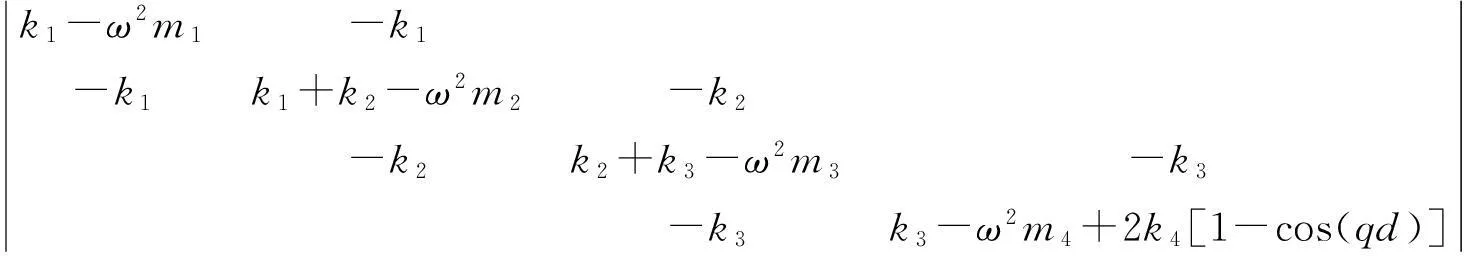
(15)

由(15)式可得频率ω对波矢qd的变化，即无限周期质量-弹簧晶格系统的能带结构。

2结果与讨论

2.1参数对有效质量的影响

根据(8)式，图3给出三谐振系统各参数(θ4、θ2、θ3、δ3、δ2)对有效质量的影响，在讨论某个参数(如θ4)对有效质量影响时，其他参数(如θ2、θ3、δ3、δ2)取1。参数θ4的影响如图3a所示，可以看到负有效质量出现，其起始频分别在ωn为0.44、1.23和1.81处，θ4的取值几乎不影响负有效质量出现的位置。随着θ4增加(如θ4=6)，前两个负有效质量频带合并，组成了一个宽带(ωn从0.44到1.25)。

图3不同参数值对三谐振系统有效质量的影响

Fig.3The impacts for effective mass of three-resonant system by different parameters

图3b展示θ2对有效质量的影响，θ2分别取1、2、6时对应的第一个负有效质量频带的起始频分别为0.44、0.49和0.51，所以随θ2增加，负有效质量频带向高频域移动。值得注意的是，θ2增加到一定值时(如图中θ2=6时)，第3个负有效质量频带有延伸至第2个负有效质量频带的趋势，这种趋势将导致一个超宽带的出现(从1.25到3.6左右)。

图3c展示θ3对有效质量的影响，θ3分别取1、2、6时对应的第一个负有效质量频带的起始频分别为0.44、0.45和0.46，截止频分别为1、0.77和0.71，所以增加θ3负有效质量频带向高频域移动而带宽变窄。

图3d展示δ3对有效质量的影响，值得注意的是δ3极大拓展了负有效质量出现的频域范围(ωn从0.265到7.08)，δ3分别取0.2、2、4时对应的第一个负有效质量频带的起始频分别为0.57、0.34和0.26，截止频分别为1、0.71和0.56，可见增加δ3负有效质量频带向低频移动而带宽变窄，但在各自的第三个负有效质量频带这种变化相反。

图3e给出了δ2对有效质量的影响，δ2分别取0.2、2、4时对应的第一个负有效质量频带的起始频分别为0.51、0.38和0.31，截止频分别为1.29、0.74和0.54，即增加δ2负有效质量频带向低频移动而带宽变窄。

2.2参数对带隙的影响

由(15)式可得无限周期晶格系统中存在波模对应的角频率与波矢(在第一布里渊区取值)关系。参数k1对带隙的影响如图4所示，其中数值仿真参数分别取m1=m2=m3=m4=1 kg，k2=1×106N/m，k3=1×106N/m，k4=1×106N/m，k1的不同值分别取为0.5×106、1×106、3×106N/m。由文献[23]可知,图中最低的一条曲线对应的波模式称为声学波，其他三条为光学波。可见具有三谐振单元的质量-弹簧晶格系统有3个带隙，当k1=0.5×106N/m时，如图4a所示，带隙分别为397~670、956~1 194、1 613~1 768 rad/s。当k1=1×106N/m时，如图4b所示，带隙分别为416~765、1 183~1 414、1 759~1 848 rad/s。当k1=3×106N/m时，如图4c所示，带隙分别为428~824、1 362~1 627、2 297~2 583 rad/s。可见增加k1可将带隙向高频移动，同时有一定拓宽带隙作用。

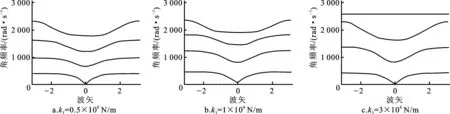
图4　不同k1值对带隙的影响

参数m1对带隙的影响如图5所示，其中数值仿真参数分别取m2=m3=m4=1 kg，k1=k2=k3=k4=1×106N/m。当m1=0.1 kg时，如图5a所示，带隙分别为479~868、1 339~1 564、1 908~1 950 rad/s。当m1=1 kg时，如图5b所示，带隙分别为416~765、1 183~1 414、1 759~1 848 rad/s，当m1=10 kg时，如图5c所示，带隙分别为170~501、960~1 261、1 679~1 805 rad/s。可见，增加m1不仅可以调节禁带带宽，且可以将禁带向低频区域移动。工程技术中对低频弹性波的处理(如水下低频波吸收，空气中小于400 Hz噪音处理，精密仪器平台隔振等)比较困难，此问题的解决可以通过参数对带隙进行调控，进而设计出低频宽带弹性波超材料。

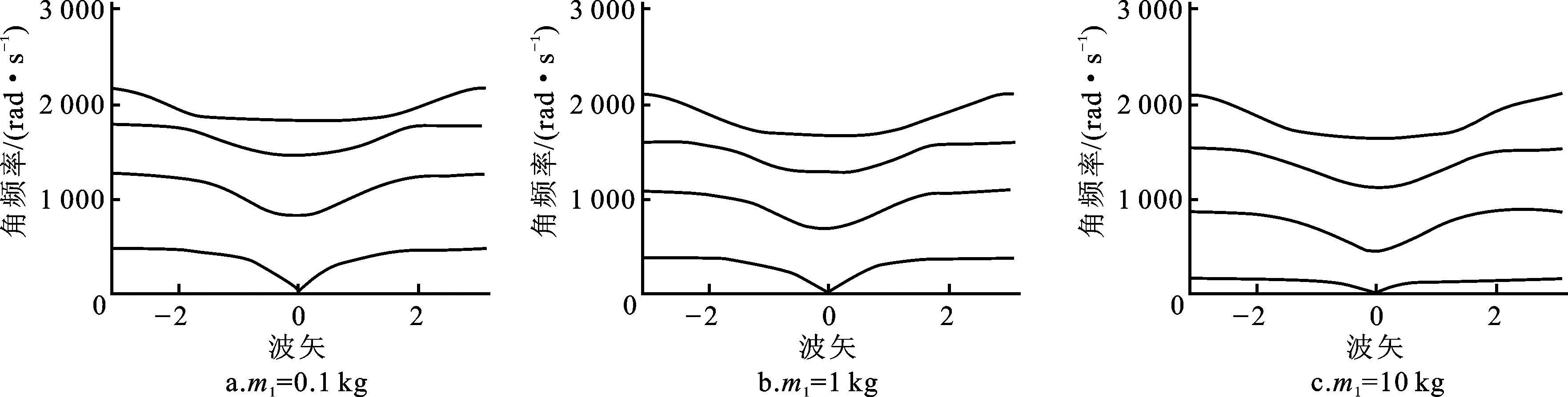
图5　不同m1值对带隙的影响

3结论

本文设计了三谐振质量-弹簧微结构，将微结构用弹性系数相等的线性弹簧链接，构成了一维无限周期质量-弹簧晶格系统，此系统相当于一种新型弹性波超材料。数值模拟了三谐振系统有效质量和无限周期质量-弹簧晶格中弹性波传播情况。得出：

(1) 三谐振系统有效质量具有频率依赖性，且3个频率位置处有效质量为负值，其位置和带宽可由5个模型参数调节。

(2) 无限周期质量-弹簧结构相当于一维声子晶体结构，相比单原子链模型其能带结构更加丰富，材料存在3个带隙。

(3) 超材料禁带可调，增加内部谐振子弹性系数可将带隙向高频移动同时有拓宽带隙作用，其质量增加可使带隙向低频移动，材料尺寸、弹性波传播波速不影响带隙频率，选择适当参数可设计低频宽带弹性波超材料。

参考文献:

[1] VESELAGO V G. The electrodynamics of substances with simultaneously negative values of ε and μ[J]. Soviet Physics Uspekhi, 1968, 10(4): 509-514.

[2] PENDRY J B, HOLDEN A J, ROBBINS D J, et al. Magnetism from conductors and enhanced nonlinear phenomena[J]. Transactions on Microwave Theory and Techniques, 1999, 47(11): 2075-2084.

[3] PENDRY J B. Negative refraction makes a perfect lens[J]. Physical Review Letters, 2000, 85(18): 3966-3969.

[4] 刘亚红, 罗春荣, 赵晓鹏. 同时实现介电常数和磁导率为负的H型结构单元左手材料[J]. 物理学报, 2007, 56(10): 5883-5889.

[5] YABLONOVITCH E. Inhibited spontaneous emission in solid-state physics and electronics[J]. Physics Review Letters, 1987,58(20):2059-2062.

[6] JOHN S. Strong localization of photons in certain disordered physics dielectric superlattices[J]. Physics Review Letters,1987,58(23): 2486-2489.

[7] JENSNO J S.Phononic band gaps and vibrations in one-and two-dimensional mass-spring structures[J]. Journal of Sound and Vibration, 2003, 266(5): 1053-1078.

[8] CHAN C T, LI J S, FUNG K H. On extending the concept of double negativity to acoustic waves[J]. Journal of Zhejiang University Science A, 2006, 7(1): 24-28.

[9] 温激鸿, 王刚, 郁殿龙, 等. 声子晶体振动带隙及减振特性研究[J]. 中国科学(E辑:技术科学), 2007, 37(9): 1126-1139.

[10] LAZAROV B S, JENSON J S. Low-frequency band gaps in chains with attached non-linear oscillators[J]. International Journal of Non-linear Mechanics, 2007, 42(10): 1186-1193.

[11] 林国昌, 孙宏伟, 谭惠丰, 等. 一种超材料梁对机械波振动吸收的模拟研究[J]. 物理学报, 2011, 60(3):360-366.

[12] 刘红星, 吴九汇, 沈礼, 等. 声子晶体机构低频降噪机理研究及应用[J]. 南京大学学报(自然科学版), 2013, 49(4): 530-537.

[13] BARAVELLI E, RUZZENE M. Internally resonating lattices for bandgap generation and low-frequency vibration control[J]. Journal of Sound and Vibration, 2013, 332(25): 6562-6579.

[14] LIU Z Y, CHAN C T, SHENG P. Analytic model of phononic crystals with local resonances[J]. Physical Review B, 2005, 71: 014103.

[15] 沈平, 梅军, 刘正猷, 等. 动态质量密度和声学超常介质[J]. 物理, 2007, 36(1): 1-6.

[16] HUANG H H, SUN C T, HUANG G L. Theoretical investigation of the behavior of an acoustic metamaterial with extreme Young′s modulus[J]. Journal of the Mechanics and Physics of Solids, 2011, 59(10): 2070-2081.

[17] WANG X D. Dynamic behavior of a metamaterial system with negative mass and modulus[J]. International Journal of Solids and Structures, 2014, 51(7): 1534-1541.

[18] HUANG H H, SUN C T, Huang G L. On the negative effective mass density in acoustic metamaterials[J]. International Journal of Engineering Science, 2009, 47(4): 610-617.

[19] LIU Y Q, SU X Y, SUN C T. Broadband elastic metamaterial with single negativity by mimicking lattice system[J]. Journal of the Mechanics and Physics of Solids, 2015, 74(1): 158-174.

[20] 赵琳瑶，张婷，刘锦锋, 等. 声波在声子晶体中的Zener共振遂穿效应[J]. 陕西师范大学学报(自然科学版), 2012, 40(3): 27-32.

[21] 郭建中, 张婷, 赵琳瑶, 等. 声波在声子晶体禁带边缘处的动态演化[J]. 科学通报, 2013, 58(1): 63-68.

[22] 徐永刚, 朱海飞, 林富锟, 等. 声学腔内声波隧穿效应的研究[J]. 陕西师范大学学报(自然科学版), 2014, 42(5): 20-26.

[23] 黄昆. 固体物理学[M] . 北京: 高等教育出版社, 1988: 82-97.

[24] 杜功焕, 朱哲民, 龚秀芬, 等. 声学基础[M] . 南京: 南京大学出版社, 2001: 3-13.

〔责任编辑 李博〕

第一作者： 张楠，女，硕士研究生，研究方向为统计物理学与复杂系统。E-mail:zhangnansnnu@163.com

Study on band gaps in elastic wave metamaterials with three-resonators

YANG Houlu, WANG Gongzheng*， MO Runyang， SU Guimei， HU Jing

(School of Physics and Information Technology, Shaanxi Normal University,

Xi′an 710119, Shaanxi, China)

Abstract:The lumped element model is present to study the band gaps of elastic wave metamaterials with three resonators.The effects of parameters on band structure and effective mass are discussed numerically. The results show that the effective mass tightly depends on frequency.The negative effective mass can be found at three positions on frequency domain.The metamaterial have three band gaps and the larger spring constant can broaden band gaps and shift band gaps to higher frequency domain.As increasing the resonator′s mass band gaps can be shifted to the low frequency domain.The metamaterial with low frequency and broad band can be desigened by property parameters.

Keywords:elastic wave；metamaterials; negative effective mass; band gap

通信作者：* 金涛，男，副教授。E-mail:jintao@snnu.edu.cn

基金项目：国家自然科学基金(11147020)； 中央高校基本科研业务费专项资金(GK201102028)

收稿日期：2015-07-09

doi:10.15983/j.cnki.jsnu.2016.01.213

文章编号：1672-4291(2016)01-0034-05

中图分类号:O421

文献标志码:A