卫星周期桁架结构振动特性应用研究

程世祥，张志谊，江　浩，张　利（.上海卫星装备研究所第二研究室，上海0040；.上海交通大学振动冲击噪声研究所，上海0040）



卫星周期桁架结构振动特性应用研究

程世祥1，张志谊2，江浩1，张利1
（1.上海卫星装备研究所第二研究室，上海200240；2.上海交通大学振动冲击噪声研究所，上海200240）

摘要：从微分方程出发，利用谱元法推导梁的解析解，并验证其准确性，以此研究平面周期桁架结构振动传递特性，即带隙和波形转换作用；根据卫星主承力结构桁架周期性特点，建立服务舱和载荷舱简化模型，利用谱元法分析其振动传递带隙特性，并进行试验验证。理论和试验表明：周期桁架结构具有良好的隔振特性，尤其是阻带内振动得到很大衰减，说明周期桁架在卫星主结构隔振设计中具有广阔应用前景。

关键词：振动与波；谱元法；振动特性；周期桁架；带隙；试验验证

桁架结构具有重量轻、简单、易于安装和拆卸等特点，在航天器结构设计中应用广泛。

国外卫星桁架式主结构设计趋近成熟，主要包括三菱柱构型、四边形构型、多边形构型和圆柱型构型。2011年5月竣工的“国际空间站”即采用了桁架挂舱式构型，以组装式或展开式桁架为基础，将多个舱段和设备安装在桁架上。国内桁架结构研究起步较晚，主要用于载荷支架和天线等非主承力结构中，但卫星平台桁架结构研究已成为当前热点。周徐斌[1]对桁架结构技术应用现状进行详细介绍；关富玲等[2]就复环桁架在卫星可展开天线中的设计和力学分析进行应用研究。国内外学者对周期结构进行了大量研究[3, 4]：主要包括建模方法和振动特性。周期结构的强迫响应求解有均匀化方法，传递矩阵法[5]，波向量法[6]以及最近的子结构迭代方法[7]和波有限元法[8]等。研究表明：周期结构具有特殊的带隙特性和波形转换作用，隔振特性良好。

新一代高分辨率卫星对平台稳定性提出了更高的要求，桁架式卫星平台承载比高，已成为卫星结构设计中的趋势。鉴于此，就周期桁架结构在整星中的振动传递特性开展初步研究，利用周期桁架主结构减少平台振动传递至载荷的响应，保证高精度载荷有效运行。

1　周期桁架结构振动传递特性

1.1周期桁架结构振动机理

理论和实验表明[9]：弹性波在结构或材料呈周期性结构中传播时，将形成特殊的色散关系——带隙，频率处于禁带内的弹性波及振动不允许通过。另一方面，周期桁架结构中组合接头对压杆中传播的纵波、扭转波和弯曲波起到散射作用，使波型发生交叉变化，各波型能量趋于一致；同时，振型波在结构中反射、透射和散射使传播距离增加，阻尼耗散作用增大，因而隔振特性良好。

1.2周期桁架结构响应解析解获取

从连续均匀梁的振动微分方程出发，推导梁的动态刚度矩阵，结合二维和三维空间坐标变换矩阵，组装出空间周期桁架结构总刚度矩阵，即可获取周期桁架结构强迫响应解。

如图1所示的均匀直梁，长度为L，密度为ρ，A为横截面积，E为弹性模量，I为截面惯性矩。梁两端分别受横向力N和弯矩M，每个端点有转角和横向位移两个自由度，分别为ϕ和w，下角标1和2分别表示梁的左端和右端。

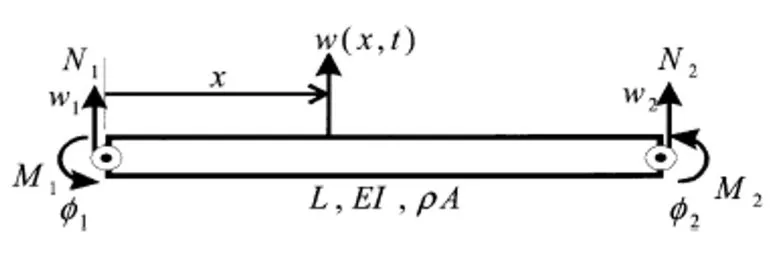
图1　梁横向振动受力示意图

对于截面恒定伯努利梁，泰勒展开式略去高次项，横向振动微分方程经Laplace变换后如式(1)所示。

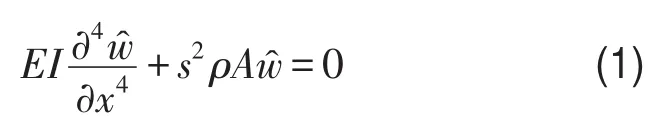
在这里，^符号表示函数是Laplace变换形式，式(1)通解可用常数c1～c4表示为式(2)的形式，其中kb为波数，梁两端的节点位移和转角为ϕ和w，与下标的关系如式(4)所示。

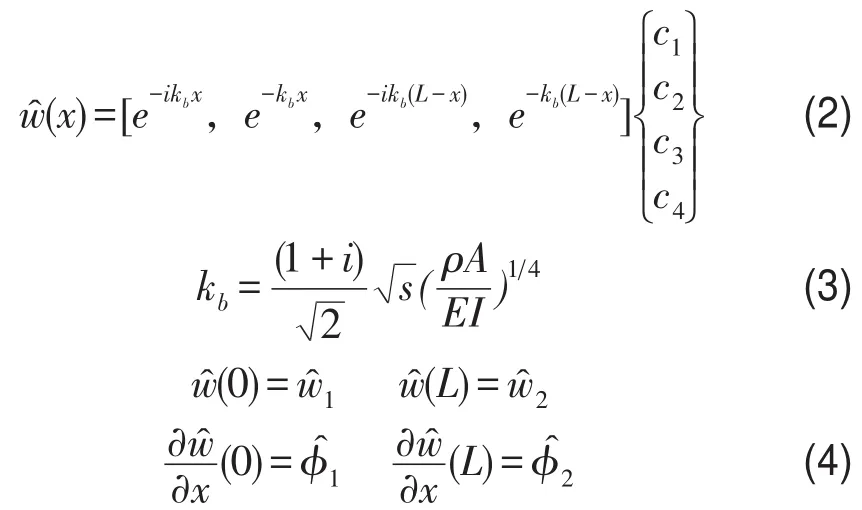
将式(4)梁两端位移代入式(2)，即可得到边界位移、转角与常数c1～c4之间的关系，利用矩阵A表示，则式(2)可用边界处位移和转角表示如下

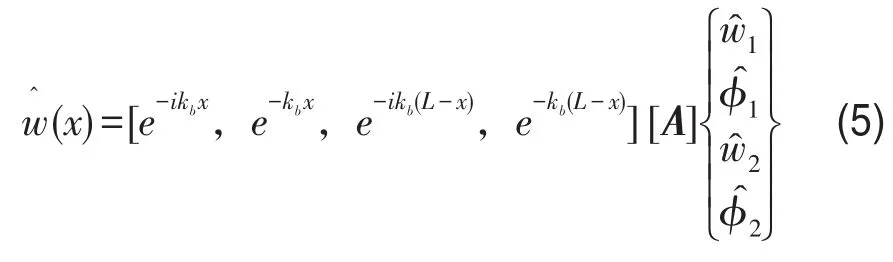
边界横向位移和端点外力的关系为

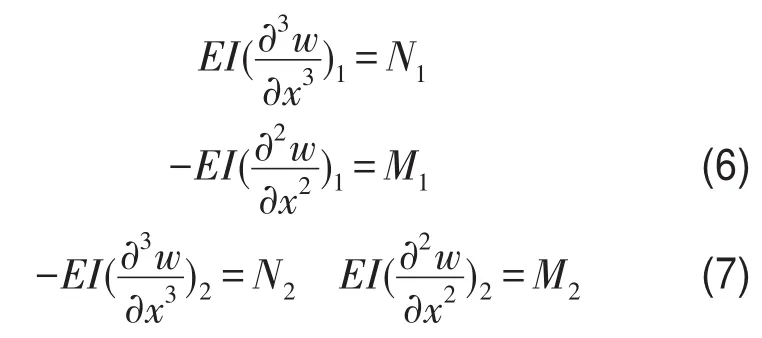
根据式(5)—式(7)，即可得出梁两端外力与两端横向位移、转角的关系，即F4×1=K4×4×X4×1

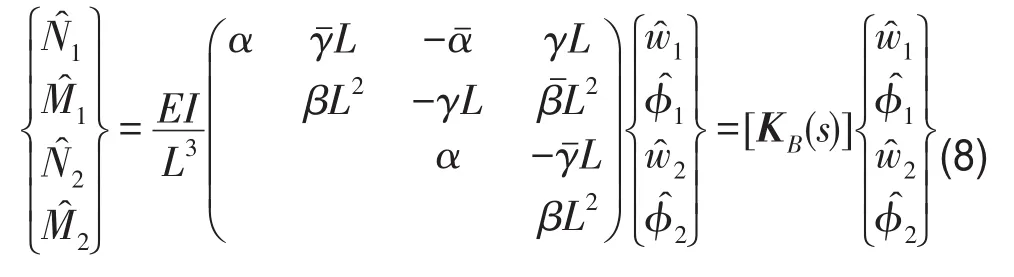
式中

工程中梁结构还经常受轴向力和扭转力矩作用，均匀梁轴向振动和扭转振动受力如图2所示，其中G为弹性模量，J为转动惯量，轴向振动时两端受力F1、F2，所受外扭矩分别为为T1、T2，转角位移用Ψ表示，轴向位移用μ表示，下角标1和2分别表示梁的左端和右端。

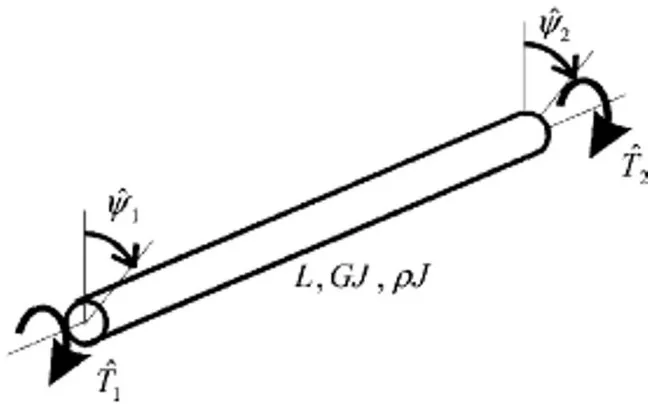
图2　轴向振动受力和扭转振动受力示意图

类似横向振动推理方法，可以得出两端作用外力与位移之间的动态刚度矩阵，分别为式(9)和式(10)，其中

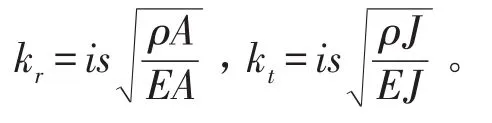
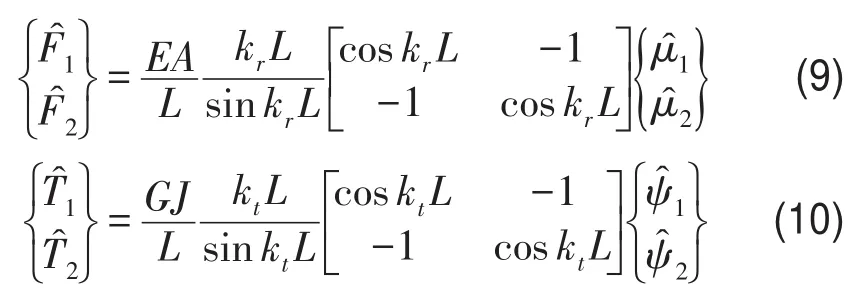
对于空间二维和三维桁架结构，不考虑扭转，每个梁的动态刚度矩阵分别为6×6和12×12矩阵，各桁架安装角度和方向不一致，动刚度矩阵组装时需进行坐标变换。设局部坐标系中刚度矩阵为K′，局部与总体坐标系变换矩阵为L，则组装到总体刚度矩阵的中矩阵K=LTK′L。三维空间桁架总刚度矩阵形式与二维类似，此处仅给出二维矩阵，如式(11)所示。

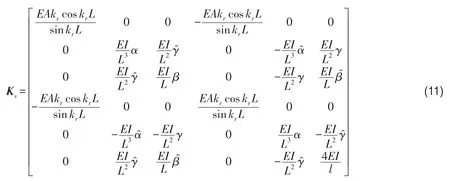
2　周期桁架数值算例

2.1谱有限元法准确性验证

利用谱元法（SEA）通过Matlab编程计算的频响解析解与有限元法（FEA）数值解对比，证明谱元法的准确性。简单平面桁架模型如图3所示，其几何结构参数如下：设均匀直梁截面为矩形截面，长宽为0.03 m×0.03 m，L＝0.4 m，E=2×1011Pa，ρ＝7 800 kg/ m3，I=6.25×10-8m4，A=9×10-4m2。桁架下端简支固定，在1号点施加正弦单位载荷情况下，计算2、3号点的频率响应。

利用本文的方法分别进行了桁架结构频散特性和带隙的求解，结果如图4、图5所示。

图4表明，谱元法求得的解析解和有限元法计算的数值解在0～2 000 Hz之内完全吻合，高频2 000 Hz以上出现了少许偏差，总体满足工程需求。

图5表明，周期桁架结构带隙明显，具有良好的隔振效果，在600 Hz～800 Hz、1 300 Hz～17 00 Hz、1800 Hz～2200 Hz均存在较明显的“阻带”。

2.2平面周期桁架结构振动传递特性

在空间桁架结构中，各桁架安装角度和方向不一致，在进行总刚度矩阵组装时需进行坐标变换。

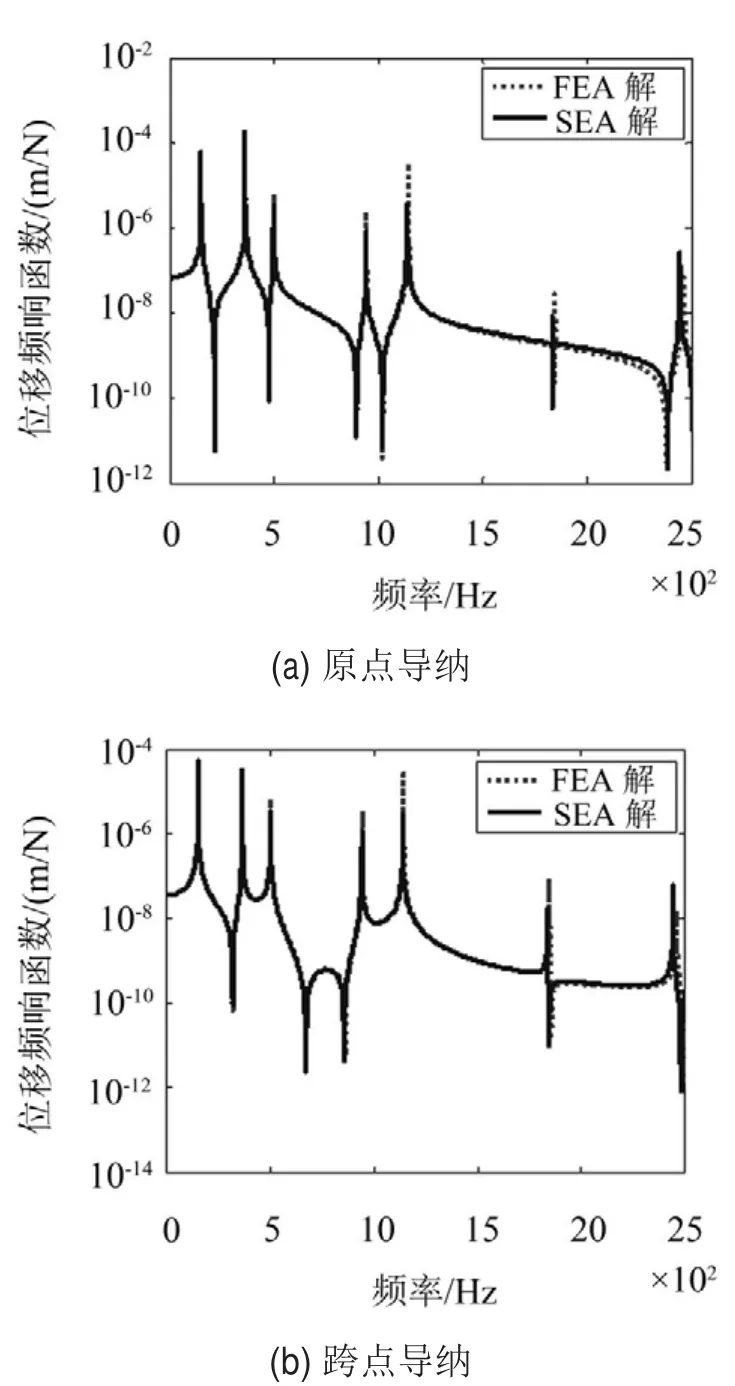
图4　平面桁架结构跨点导纳对比

如图6所示的平面桁架结构，基本单元高0.2 m，长度0.4 m。截面尺寸与3.1节桁架保持一致，在1号点基于正弦单位载荷激励，利用谱元法计算2—4号点频响函数。

计算结果如图7所示。周期桁架结构位移响应从上至下振动衰减明显；由于在组合接头处强制发生波形转换和周期结构特性，并且在相邻共振频率之间产生了很明显的带隙，尤其是1 000 Hz～2 000 Hz之间，周期结构不同，其振动衰减幅度和禁带范围也不相同，周期数目越多，衰减幅度越大。

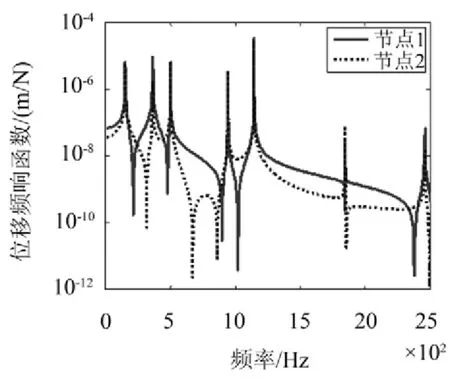
图5　谱元法求解平面桁架结构的振动传递特性

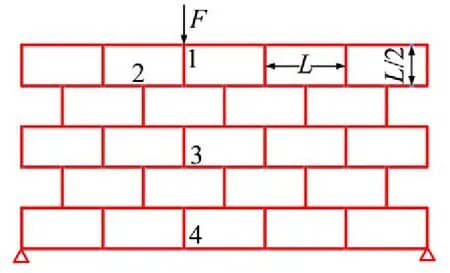
图6　平面周期桁架结构示意图

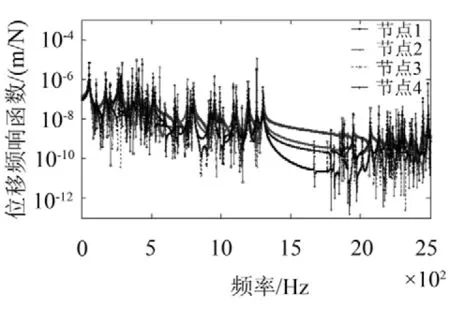
图7　平面周期桁架结构振动传递特性

2.3空间周期桁架结构振动传递特性

某卫星主结构平台采用桁架式结构，框架呈周期性，框架之间为碳纤维隔板和平板，平台主结构周期桁架简化如图8所示。

图8　卫星简化周期桁架结构示意图

卫星采用内外正六边形构型，外层六边形顶点处包络圆半径1.68 m；内六边形包络圆半径0.48 m，其中低层为0.78 m。卫星简化桁架周期数为3，层高0.7m。谱元法计算时材料特性参数为碳钢。

谱元法计算结果如图9所示，周期桁架结构位移响应从上至下振动衰减明显；由于在组合接头处强制发生波形转换和周期结构特性，在部分频段出现“阻带”，平面桁架结构中1 300 Hz～1 800 Hz，卫星桁架结构在200 Hz～290 Hz、520 Hz～700 Hz、930 Hz～1000 Hz区域尤为显著。

图9　卫星周期桁架结构振动传递特性

3　卫星周期桁架结构振动特性验证

平面周期结构和卫星三维桁架结构均表明周期桁架结构具有良好的隔振特性，为了进一步验证，针对2.3小节中进行桁架结构简化的某卫星进行了振动传递特性测试。激励源为卫星底部隔板上活动部件飞轮，从下至上测量第二层隔板响应点9、第三层隔板响应点10和服务舱顶板11号点响应，具体位置如图10所示。

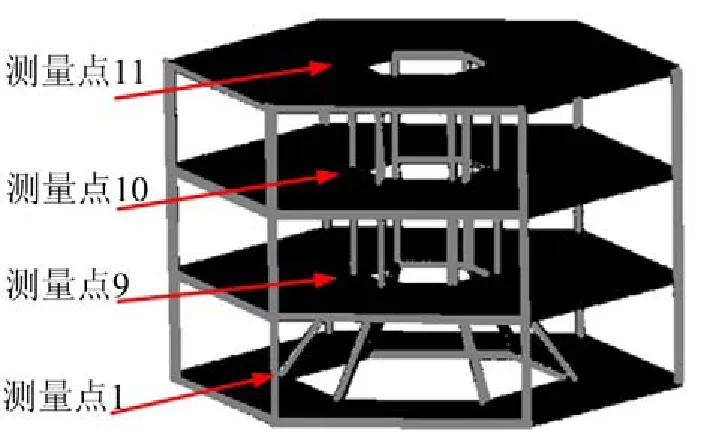
图10　卫星振动试验测点示意图

试验测试了飞轮从0至5 000 r/min加速过程中响应点幅值的时间历程和频域响应，试验结果如图11所示。

试验与简化模型的谱元法计算结果趋势总体基本相符，结果表明，卫星中的周期桁架结构从下至上振动衰减明显，尤其是在高于300 Hz时。同时，在400 Hz～700 Hz之间出现较明显的带隙特征，在该频段频率响应衰减达到10dB。

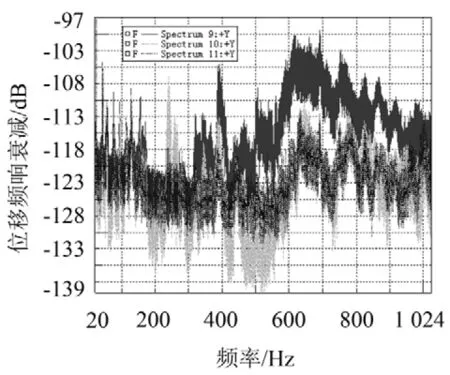
图11　卫星周期桁架结构频域振动传递特性

4　总结

对于周期结构，谱元法解析解与有限元法结果吻合良好，本文利用谱有限元方法系统地研究了周期桁架结构的振动传递特性，并计算了卫星简化的周期桁架结构振动传递特性，最后，通过卫星振动传递特性试验进行验证。

结果表明：周期桁架结果具有特殊的带隙特性，高频和“阻带”内隔振效果良好，在新一代高精度卫星对结构传递隔振特性要求日益严格的情况下，周期结构在新一代卫星结构设计中具有广阔的应用前景。

参考文献：

[1]周徐斌.卫星桁架结构技术综述[C].中国宇航学会飞行器总体专业委员会2006年学术研讨会论文集.上海：中国宇航学会飞行器总体专业委员会，2006：390-395.

[2]关富玲，徐彦.结构中弹性波与振动局部化问题的研究[J].载人航天，2011，(2)：24-29.

[3]李凤明.结构中弹性波与振动局部化问题的研究[D].哈尔滨：哈尔滨工业大学，2003.

[4] Gonella S, Ruzzene M. Homogenization of vibrating periodic lattice structures[J]. Applied Mathematical Modelling, 2008, 32(4):459-482.

[5] Luongo A, Romeo F. Real wave vectors for dynamic analysis of periodic structures[J]. Journal of Sound and Vibration, 2005, 279(1-2):309-325.

[6] Gry L, Gontier C. Dynamic modelling of railway track:A periodic model based on a generalized beam formulation [J]. Journal of Sound and Vibration, 1997, 199(4):531-558.

[7] Duhamel D. A recursive approach for the finite element computation of waveguides[J]. Journal of Sound and Vibration, 2009, 323(1-2):163-172.

[8] Waki A. On the application of finite element analysis to wave motion in one- dimensional waveguides[D]. UK:Southampton University, 2007.

[9]黄修长，冯国平，张志谊，等.周期结构机械滤波器对浮筏隔振系统传递特性的影响[J].噪声与振动控制，2010，30(2)：9-12.

Research of Vibration Characteristics of Periodic Truss Structures in Satellites

CHENG Shi-xiang1，ZHANG Zhi-yi2，JIANG Hao1，ZHANG Li1
( 1. Shanghai Instituteof Spacecraft Equipment, Shanghai 200240, China; 2. Instituteof Vibration, Shock & Noise, Shanghai Jiaotong University, Shanghai 200240, China)

Abstract:Theanalytical result of periodic trussstructureswasdeduced by Spectrum Element Method (SEM), and then validated by FEM. The vibration transfer characteristics of the periodic truss structures, such as the band gap and the waveform conversion mechanism, were analyzed and proved. Based on the results, a simplified periodic truss model of the satellite structure was established, and the dynamic transfer trait was analyzed with the SEM and experiments. The simulation and experiment results show that the periodic truss structure has better vibration isolation properties. Especially, the vibration is greatly reduced in pass band. So the periodic truss has a great application foreground in satellite structure design.

Key words:vibration and wave; spectrum element method; vibration characteristic; periodic truss; band gap; experiment varification

作者简介：程世祥（1987-），男，湖北黄冈人，硕士，研究方向为航天器力学试验技术，隔振设计研究。E-mail:chengwork1987@126.com

收稿日期：2015-05-26

文章编号：1006-1355(2016)02-0012-05

中图分类号：O328；V231.92

文献标识码：ADOI编码：10.3969/j.issn.1006-1335.2016.02.003