石墨烯磁势垒量子点的能级结构

邓立娟, 左凯丽, 阎维贤*

(1 山西大学 理论物理研究所； 2 山西大学 物理电子工程学院， 山西 太原 030006)



石墨烯磁势垒量子点的能级结构

邓立娟1, 左凯丽2, 阎维贤2*

(1 山西大学 理论物理研究所； 2 山西大学 物理电子工程学院， 山西 太原 030006)

摘要：研究了磁势垒量子点中有质量和无质量Dirac粒子的能级结构。通过求解Dirac方程，利用数值计算出圆内圆外磁矢势方向相同和相反以及有质量时量子点的能谱结构。研究表明，当圆内圆外的磁矢势方向相同时，随着量子点半径的增加，能级的变化体现出量子点内外磁场的竞争关系。与量子点内外的磁矢势方向相同显著不同，量子点内外的磁矢势方向相反时，量子点外的磁场占主导地位，其引起的朗道能级始终出现。质量的引进让系统转化为一个反量子点，且有质量Dirac粒子能级的平方获得一个跟质量相关的平移。

关键词:石墨烯量子点； 磁势垒； 能级结构

PACS: 73.22.Pr, 73.21.La, 81.05.U-

近年来，对二维具有蜂窝状结构石墨烯[1]的研究成为凝聚态物理的重要分支，其独特的力学性质、电子性质备受关注[2-3]，可能成为取代硅的新型材料。例如：强磁场会在二维电子系统的石墨烯中诱导出有别于通常半导体异质结的反常量子霍尔效应[1]，这种效应是由石墨烯中导带和价带在狄拉克点处交汇引起的。石墨烯与超导材料的异质结结构使得电子-空穴对呈现出绝缘体-超导材料异质结所没有的镜面Andreev反射[4]。理想石墨烯哈密顿跟无质量相对论粒子哈密顿相似，但有效速度约为光速的1/300，在高能物理中由于加速器能量限制而不易观察的物理现象能够通过石墨烯平台实现，这样研究石墨烯就把高能物理和凝聚态物理紧密地联系起来。

通过引入静电势垒我们可以在石墨烯上构造出类似于半导体微结构的量子阱、量子线和量子点[2]。因为石墨烯量子点中电子的手征特性，单纯的电势垒不能够完全约束电子于势垒或量子点中。Martino等人研究了磁势垒对于Dirac电子约束，发现磁势垒能有效地把Dirac电子束缚于势垒中[5]，在此基础上我们研究了应力[6-7]对这个体系的作用。基于电子电子或电子声子间相互作用能够使得无质量的狄拉克粒子的能谱打开一个能隙，而这个能隙能够认为是由于质量引起的，近来Stauber等人探讨了石墨烯量子点中内外不同质量的能谱[8]。前人所做研究一般都是纯电势引起的量子点[9-10]，或者是量子点内部没有磁场，而外部具有磁场[1,5,11]。作为磁势垒量子阱或超晶格研究的延伸，本文讨论了无质量和有质量的Dirac粒子在各种不同磁势垒下的能级，并讨论了量子点内外磁矢势的不同形态对能级的不同影响，以及能级随角动量量子数和质量变化的详细情况。

1无质量的磁势垒量子点的能级

理想石墨烯中的布里渊区有两个不等价的点K和K′(Dirac点)，在Dirac点的电子服从Driac-Weyl(DW)方程，假设实空间中相互作用不剧烈变化的情形下，则我们只需要研究点K处的动力学即可，如果考虑质量，则Dirac粒子满足如下的本征方程[11]:

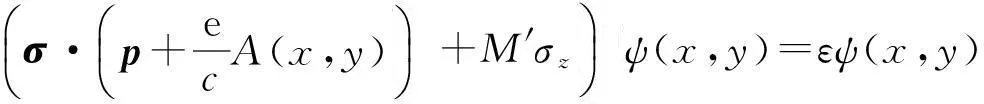
(1)

式中,费米速度vF≈106m/s,A(x,y)为矢势，M为质量，Pauli矩阵σ(σx,σy)，E=vFε,M=vFM′。

(2)

将方程(2)代入方程(1)，则得到下面的关于极坐标中极径的微分方程：

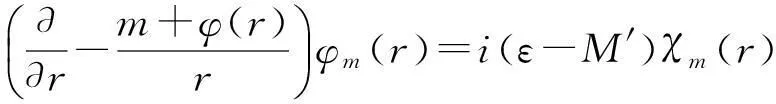
(3)

合并方程(3)可以得到一个二阶微分方程

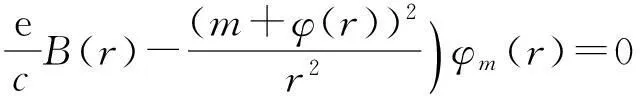
(4)

现在考虑无质量的石墨烯磁量子点模型，在石墨烯中加上垂直于表面且方向相同的磁场，在半径为R的圆外为均匀磁场B2，圆内为均匀磁场B1，则半径为R的圆内外的磁通量可以表示为

(5)

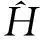
其中Nm为归一化常数。

现在讨论ε≠0时的情况：经过一系列变换，可以把方程(4)化简为Whittaker函数满足的方程，通过解方程得到波函数

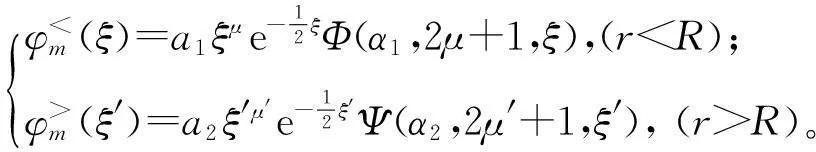
(6)

根据波函数和波函数一阶导数的连续性，可以计算出能量与量子点半径所满足的关系式

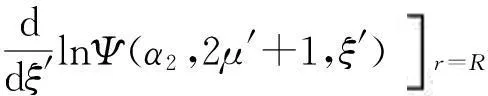
(7)

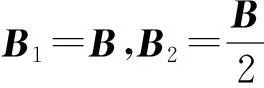
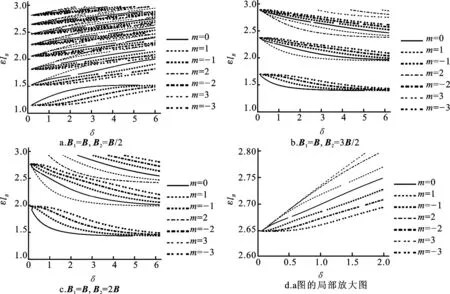
图1石墨烯磁势垒量子点低能级的能量与通量δ的关系

Fig.1The energy levels of the magnetic-barrier graphene dot versus the magnetic fluxδ

作为一种极端的磁势垒量子点情形,就是把量子点内外磁势垒所对应的磁场设置成方向相反，我们分两种情况讨论。

第一种情形：B1=B,B2=-B，仿照上面的计算过程可以得到能级满足的超越方程

(8)

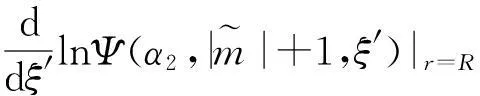
(9)

图2石墨烯磁势垒量子点能级的能量与通量δ的关系

Fig.2The energy levels of the magnetic-barrier graphene dot versus the magnetic fluxδ

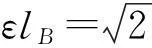
2有质量的磁势垒量子点的能级

图3　有质量情形下的能级图

3结论

本文利用解析和数值方法研究了量子点内外磁场不同时(存在磁势垒)无质量和有质量Dirac粒子的能级结构，对量子点内无磁场情形进行推广。研究发现诸多有别于量子点内无磁场下的物理现象：如果圆内圆外的磁矢势方向相同，随着量子点半径的增大，能级从对应磁场外的朗道能级逐渐向对应磁场内的朗道能级靠拢，体现出磁场内外的竞争关系；如果量子点内外的磁矢势方向相反，此时量子点外的磁场引起的朗道能级始终会出现，这显著区别于磁矢势方向相同的情形。量子点内外磁场强度的变化表现为能级随角动量量子数的变化是由于磁通量跟角动量量子数既有协同也有竞争关系。质量的引进让Dirac粒子能级的平方获得一个跟质量相关的有限的平移。本文讨论了磁势垒下量子点系统的束缚态，没有涉及散射态的反射率和透射率，磁势垒量子点对入射的平面波散射和反射有待今后进一步研究。

参考文献：

[1] NETO A H C, GUINEA F, PERES N M R, et al. The electronic properties of graphene[J]. Review Modern Physics, 2009, 81:109-162.

[2] PERES N M R, RODRIGUES J N B, STAUBER T, et al. Dirac electrons in graphene-based quantum wires and quantum dots[J]. Journal of Physics: Condensed Matter, 2009, 21: 344202(1-18).

[3] YAN W X. Graphene quantum wells and superlattices driven by periodic linear potential[J]. Chinese Physics Letters, 2013 30: 047202(1-4).

[4] BEENAKKER C W J. Specular Andreev reflection in graphene [J]. Physical Review Letters, 2006, 97:067007(1-4).

[5] DE MARTINO A, DELL′ANNA L, EGGER R. Magnetic confinement of massless Dirac fermions in graphene[J]. Physical Review Letters, 2007, 98: 066802(1-4).

[6] YAN W X, MA L N. Dirac electron in the various strained graphene stripes immersed into the magnetic barriers[J]. Physica B, 2014, 445: 28-36.

[7] 王恬，张琳，阎维贤. 交-直流势驱动下的应力石墨烯势垒中Dirac粒子的隧穿[J]. 华中师范大学学报(自然科学版), 2014, 48(6): 821-828.

[8] GUTIERREZ-RUBIO A, STAUBER T. Mass-profile quantum dots in graphene and artificial periodic structures[J].Physical Review B, 2015, 91: 165415(1-12).

[9] HEWAGEEGANA P, APALKOV V. Electron localization in graphene quantum dots[J]. Physics Review B, 2008, 77: 245426(1-8).

[10] HEWAGEEGANA P, APALKOV V. Trapping of an electron in coupled quantum dots in graphene[J]. Physical Review B, 2009, 79: 115418(1-9).

[11] PARK P S, KIM S C, YANG S R E. Electronic properties of a graphene antidot in magnetic fields[J].Journal of Physics: Condensed Matter, 2010, 22: 375302(1-7).

[12] OLDHAM K, MYLAND J, SPANIER J. An atlas of functions[M].2nd ed.Heidelberg: Springer-Verlag, 2009.

〔责任编辑 李博〕

第一作者： 吴佳，女，硕士研究生，研究方向为纳米材料的光学分析。E-mail: wujia19910113@163.com

The energy-level structures of the graphene quantum dot

induced by the magnetic barriers

DENG Lijuan1, ZUO Kaili2, YAN Weixian2*

(1 Institute of Theoretical Physics, Shanxi University； 2 College of Physics and Electronics

Engineering, Shanxi University, Taiyuan 030006, Shanxi, China)

Abstract:The energy-level structures of the graphene quantum dot influenced by magnetic barrier is investigated.Under the condition of the magnetic fields inside and outside the dot are parallel, as increase of the dot size,the energy-level structure are determined by the competition of two magnetic. The accompanying Landau levels from the field outside the dot always appear when the directions of the two vector potentials are mutually anti-parallel. The addition of the mass makes the dot to be an antidot, whereas the squared energy levels gain a constant associated with the mass.

Keywords:graphene quantum dot; magnetic barriers; energy-level structures

通信作者：* 李保新，男，教授，博士生导师。E-mail: libaoxin@snnu.edu.cn

基金项目：国家自然科学基金(21275096)

收稿日期：2015-02-09

doi:10.15983/j.cnki.jsnu.2016.01.311

文章编号：1672-4291(2016)01-0054-06

中图分类号:O469

文献标志码:A