认知诊断模型资料拟合检验方法和统计量*

陈 孚 辛 涛 刘彦楼 刘 拓 田 伟

(1北京师范大学心理学院;2北京师范大学中国基础教育质量监测协同创新中心,北京 100875)

(3曲阜师范大学中国教育大数据研究院,曲阜 273165)(4天津师范大学教育科学学院,天津 300384)

1 引言

作为新一代测验理论,认知诊断理论在过去的几十年间成为了测量学界研究的热点。认知诊断评价结合了认知心理学理论和统计模型,通过被试在测验中的实际作答反应获得被试在所考察的认知技能(或称之为“属性”)上的掌握情况,从而实现对个体知识结构、加工技能或认知结构进行诊断评估(Leighton&Gierl,2007)。通过认知诊断模型(cognitive diagnosticmodels,CDM s)对测验数据的分析,被试可获得其知识或技能掌握情况的精细化报告,使用者也可达到形成性和诊断性评价的目的(Embretson,1998;Tatsuoka,1983)。据统计,现有的认知诊断模型多达100多种(辛涛,乐美玲,张佳慧,2012),这些模型对所考察属性与作答反应关系的假设往往是不同的。对于认知诊断实践而言,如何从众多模型中选择合适的模型？又如何评价所选的模型与数据之间的匹配程度？模型资料拟合检验能够为这些决策提供重要的参考指标。

和其它统计模型的拟合检验类似,CDM拟合检验可分为三个方面：模型资料全局或整体拟合检验(global/overallmodel-data fit)考察在整体水平上模型是否良好匹配数据,项目拟合(item fit)检验考察测验中的部分项目是否拟合所选模型,个人拟合(person fit)检验考察参加测验的被试是否适用于所选模型。需特别说明的是,CDM对被试的诊断分类应基于Q矩阵被正确界定的前提下进行,因此对Q矩阵正确性的检验也应纳入CDM拟合检验的一部分,但由于篇幅有限,且Q矩阵的修正和估计方法内容丰富,已有相关综述发表(刘永,涂冬波,2015),本文在此略去。拟合检验的另一种分类方式是相对拟合检验和绝对拟合检验,前者用于多个模型对同一批数据的拟合情况比较,从而通过最优的拟合指标选择最适用于分析和诊断的模型,后者用于考察某个特定的模型与数据的拟合情况。

然而,传统的基于卡方的拟合检验方法不适用于CDM,这是由CDM的特性及卡方检验的使用条件所决定的(Rup p,Tem p lin,&Henson,2010)。卡方检验必须遵循的应用条件为足够大的样本量,以确保在列联表中每个单元格的期望频数不少于5(Agresti&Finlay,1997)。在认知诊断测验中,少量的题目就可能产生大量的期望作答反应模式。如果样本量较小,较大数量的期望作答反应模式就易导致列联表中的很多单元格不存在观测值。例如,一个包含30题的认知诊断测验,可能的作答反应模式超过10亿种,但实际中被试数量却有限,因此大量的期望反应模式在实际样本中无法被观测到,此时便造成列联表稀疏(sparse)问题。在该情形下,使用卡方检验会使检验所犯的一类错误率急剧增大。一般而言,传统的卡方检验只适用于认知诊断测验题目少于10~12个的情况(Sinharay&A lmond,2007),但该情况在认知诊断实践中并不多见。

尽管CDM拟合检验面临困境,但已有不少研究者在重复抽样技术(resampling techniques)、后验预测模型检查(posterior predictivemodel checking,PPMC)方法和有限信息的绝对拟合检验方法基础上提出了相应的拟合检验统计量,这些方法或统计量都能较好地用于模型选择以及模型数据失拟的评估(e.g.,de la Torre&Douglas,2008;Jurich,2014;Kunina-Habenicht,Rupp,&Wilhelm,2012)。以下部分分别对CDM的项目拟合、模型绝对拟合、模型相对拟合和个人拟合方法和统计量进行介绍和评价,最后提出对未来研究方向的思考和展望。

2 CDM项目拟合检验统计量

CDM项目拟合检验一般是绝对拟合检验。当前,研究者可使用的CDM项目拟合检验方法大致可以分为三个方面：基于传统卡方检验的拟合统计量、基于PPMC方法的拟合统计量以及基于有限信息的拟合统计量。

2.1 基于传统卡方检验的拟合统计量

此类统计量为传统的分类数据拟合统计量,用于刻画每种属性掌握模式中观测频数和模型预测的频数之间的差异。在项目反应理论(item response theory,IRT)框架中,这些统计量都服从或近似服从卡方分布。

2.1.1 统计量

对于考察K个属性的认知诊断测验而言,最多可能存在2K种属性掌握模式。此时,进行卡方检验的皮尔逊2c统计量通过下式计算而得：

其中Fjl为属性掌握模式为的被试中答对题目j的“观测”频数(该频数实际不可观测,依赖于模型参数估计结果),Ejl为模型预测的属性掌握模式为的被试中答对题目j的期望频数,K为属性个数。在样本量足够大的情况下,该统计量近似服从以自由度为的卡方分布(m为模型参数个数)。

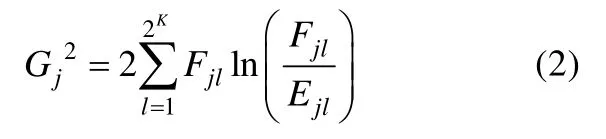
2.1.2 Q1统计量

Q1统计量是统计量的变式,其表达式如下(Yen,1981)：

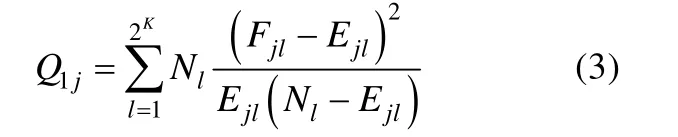
其中Nl表示被分类到属性掌握模式中被试的“观测”频数。在数据不稀疏的前提下,Q1j服从自由度为的卡方分布(m为模型参数个数)。

2.1.3 PD统计量

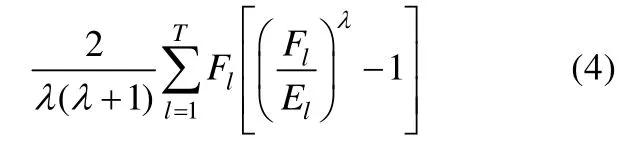
其中T为总的分组数(在CDM中,T为可能的属性掌握模式数量2K),为分组l中的观测频数,El为分组l中的期望频数。当时,该统计量为统计量;当的极限为0时,该统计量为统计量。PD统计量在取不同值时具有不同的检验力,而研究者认为是在各种情形下都具有较好检验力的适中值(Read&Cressie,1988),因此可将时构造的PD统计量运用到CDM项目拟合检验当中(Wang,Shu,Shang,&Xu,2015)：

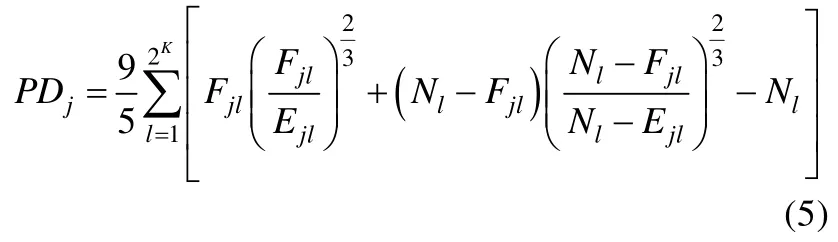
该统计量通过被试的属性掌握模式对被试进行分组。同样地,在数据不稀疏的前提下,PDj统计量服从自由度为的卡方分布(m为模型参数个数)。

2.1.4 统计量

Q1和PD统计量都依赖于被试的属性掌握模式的估计结果,因此“观测”频数实际上不可直接观测。为了避免对属性掌握模式点估计的不准确性,Wang等(2015)借鉴了Stone(2000)的思想,使用的后验分布获得每种属性掌握模式中正确作答题目j被试频数的伪数(pseudo-counts)rjl替代“观测”频数Fjl。rjl的表达式为：

由于rjl的计算依赖于属性掌握模式的先验分布以及模型参数,不同分组间的观测频数值不是相互独立的,同一名被试可以基于相应的概率被分类到不同的属性掌握模式分组中,因此该和统计量不再服从卡方分布,但可以通过蒙特卡洛重复抽样技术产生一个经验的抽样分布,作为和统计量的检验标准(Stone,2000)。

卡方类统计量的最大优点在于计算简便,易于理解。但由于卡方检验使用条件的限制,此类统计量并不能直接应用于CDM拟合检验当中(Rupp etal.,2010)。现有对上述问题的尝试的主要途径是借助蒙特卡洛重复抽样技术获得统计量的抽样分布(Bartholomew&Tzamourani,1999;Tollenaar&Mooijaart,2003),从而完成拟合检验。但由于该方法需要模拟多个数据集,且需对每个数据集重新进行参数估计和拟合统计量估计,因此实际使用需要耗费大量的时间。如果模型本身、Q矩阵以及参数估计方法较为复杂,重复抽样技术便难以应用到实践当中。因此,该方法在实际使用中并不被研究者推荐(Rupp et al.,2010),而是作为其它方法的基础。

将传统卡方类统计量直接应用于CDM项目拟合检验的研究并不多见。涂冬波、张心、蔡艳和戴海琦(2014)将和统计量运用到DINA(determ inistic inputs,noisy “and”gate)模型的项目拟合检验,通过模拟研究发现这两个统计量能有效侦查项目失拟情况,但检验效果会受测验长度、属性个数等因素的影响。Wang等人(2015)的研究探讨了和统计量在传统EM算法和PPMC方法(详见下一部分)下的拟合表现差异,结果发现在这两种估计方法下和统计量表现都较好,但这两个统计量在EM算法下的统计检验力比在PPMC方法下更高。

2.2 基于后验预测模型检查(PPMC)方法的统计量

后验预测模型检查(posterior predictivemodel checking,PPMC;Rubin,1984;Sinharay,2006;Sinharay&A lmond,2007)方法的核心是比较观测数据与模型预测数据(replicated data)在差异度量(discrepancymeasures)上的差异大小。该方法是基于贝叶斯模型的拟合检验方法,主要适用于模型参数估计基于贝叶斯框架的情形。PPMC方法一般与MCMC算法结合,基于MCMC算法中马尔科夫链上每一步得到的模型参数计算新的预测数据及拟合统计量(差异度量)用于评估模型的拟合情况。过程如下：

适用于PPMC方法的差异度量较多,主要有简单相关系数(pointbiserial correlations)、项目误差均方根、基于同分类的项目拟合统计量(item fit measures based on equivalence classmembership)、基于总分的项目拟合统计量(item fitmeasures based on raw scores)、项目间关联指标(association among the items)和平均绝对差异(mean absolute deviation)及其近似误差均方根(RMSEA)。

2.2.1 简单相关系数

该统计量使用的是被试的项目得分和个人总分之间的点二列相关Corr.,多应用于IRT模型(Lord,1980;Sinharay,2005),可评估项目之间是否等区分度(单昕彤,谭辉晔,刘永,吴方文,涂冬波,2014)。在CDM项目拟合检验中,可通过对观测的相关均值和预测的相关均值对比及PPP值判断模型对数据的拟合情况。

2.2.2 项目误差均方根

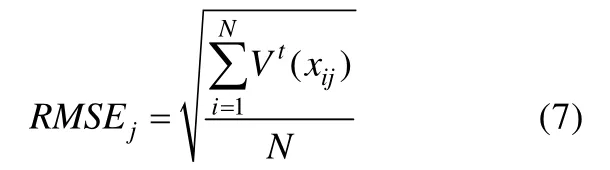
同理,在预测数据中,对项目j同样可以计算其差异度量,最后使用在所有迭代中的比例作为项目拟合好坏的指标,当该比例接近0.5时说明项目拟合较好。

项目误差均方根是一个较为保守的拟合统计量,在实际研究中不适用于项目的绝对拟合检验,因此通常作为比较项目拟合差异的相对拟合指标(Yan,M islevy,&Almond,2003)。

2.2.3 基于同分类的项目拟合统计量

此类拟合指标以同一属性掌握模式的被试在项目上的正确作答比例为构造基础,既可用于评价项目拟合,也可用于评价总体拟合。定义具有属性掌握模式的被试在项目上的正答比例为,而在预测数据中该正答比例为。其中并不能通过观测数据直接获得,而是依赖于模型参数估计值。每个题目和每种属性掌握模式的组合在MCMC算法的每一次迭代中都有对应的一组和,通过对两者的比较以及相应的PPP值即可检验项目拟合情况。由于每个项目都需对每种属性掌握模式进行差异度量的检验,因此研究者在此基础上进一步提出了两个类和类统计量用以评价项目拟合(Sinharay,2006)。

令Nk为属性掌握模式k中的人数,Ejk为具有属性掌握模式k的被试正确作答项目j的概率,可通过MCMC算法每次迭代的被试参数和模型参数计算而得。则类统计量为：

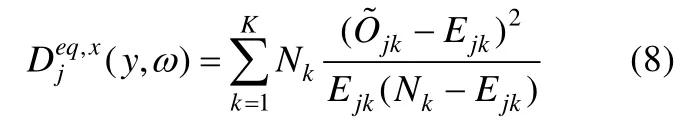
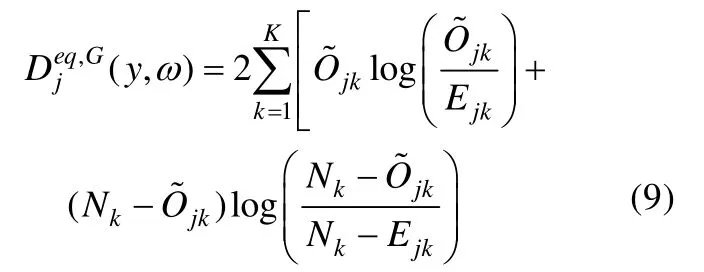
此类统计量虽然是依据卡方检验的思想构造的,但由于被试的属性掌握模式是未知的,此类统计量的参照分布并不明确,可能会影响拟合检验的实际效果。Sinharay,Almond和Yan(2004)在贝叶斯网络(Bayesian Network)框架下使用不同参数个数的模型对Tatsuoka(1990)的分数减法数据进行分析,结果发现使用类统计量对项目拟合和测验总体拟合的检验效果并不理想。因此,此类统计量的参照分布和统计检验力都需要进一步研究(Sinharay&Almond,2007)。此外,此类统计量基于被试的属性掌握模式分组,但被试的属性掌握模式不可直接观测,而是依赖模型的参数估计结果,因此如果样本量过小可能会导致属性掌握模式的估计不稳定,从而就可能影响该统计量的检验效果。研究者因此又提出了基于被试总分的项目拟合指标(Sinharay,2006)。

2.2.4 基于总分的项目拟合统计量

同样是借鉴卡方统计量的思想,但基于被试总分的项目拟合指标是以被试在测验上的原始得分作为分组依据的。定义总分为的被试在项目上的正答比例为,而在预测数据中该正答比例为。每个题目和每个总分的组合在MCMC算法的每一次迭代中都有对应的一组和,通过对两者的比较以及相应的PPP值检验便可检验项目拟合情况。和基于同分类的指标构造相同,研究者也提出了两个类和类统计量。

令Nk为获得总分k的人数,Ejk为具有总分k的被试正确作答项目j的概率,则类统计量为：

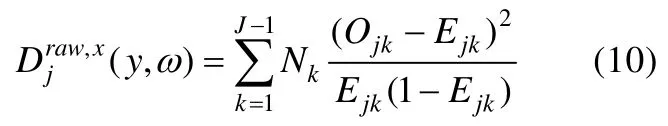
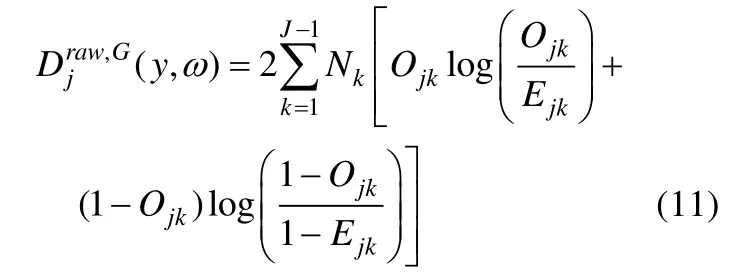
此类统计量的拟合检验方法与基于同分类的拟合统计量一致。此类统计量的优点在于通过被试总分进行分组避免了基于属性掌握模式分组的参数估计不确定性,能提高拟合检验的效果。Sinharay(2006)基于PPMC方法在贝叶斯网络框架下对这两类统计量的拟合效果进行了比较,结果发现基于总分的项目拟合统计量比基于同分类的项目拟合统计量具有更好的拟合检验效果。

2.2.5 项目间关联指标

项目间关联指标常用于IRT模型的局部独立性假设检验(Chen&Thissen,1997;Sinharay,2005;Sinharay&Johnson,2003)。令为在第一题上得k分且在第二题上得分的人数,。则可用优势比来刻画项目间关联,该统计量为：

在拟合检验中,一个完美拟合的模型应该能完全解释数据之间的关联,因此通过PPMC方法中模型预测的优势比能够考察模型对测验项目关联的解释程度,从而就能达到评价模型对数据拟合的目的。

2.2.6 平均绝对差异及其RM SEA

Kunina-Habenicht等(2012)在 Henson,Roussos,Douglas和He(2008)研究的基础上提出了基于某类属性掌握模式的被试中观测的和期望的项目正答概率的绝对差异的MAD统计量：

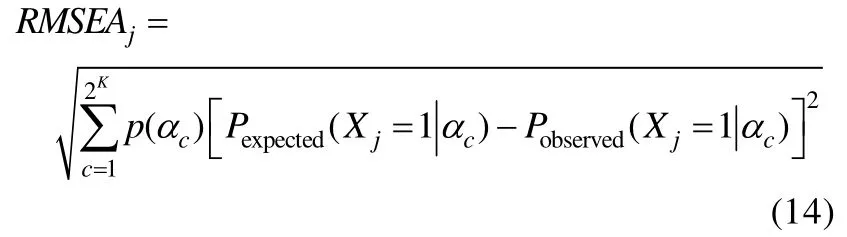
Kunina-Habenicht等(2012)通过模拟研究发现,样本量大小、测验考察的属性数量和题目所考察的属性数量都会影响MADj和的拟合效果,样本量越大,统计检验力越高。此外,的统计检验力相比于MADj稍高。

2.2.7 小结

PPMC方法的最大优点在于其使用了参数的后验预测分布,有效避免参数估计不稳定的问题,即使在样本量很小的情形下也可以较好使用。对于认知诊断模型的拟合检验,PPMC方法还是存在一些不可忽视的问题：首先,相关的模拟研究表明,PPMC方法过于保守,对于项目或测验的绝对拟合检验并不具备优良性质;其次,PPMC方法依赖于MCMC算法,而MCMC算法需要进行大量密集的计算,对实践而言也并非易事;最后,PPMC方法中的PPP值为非均匀分布(Robins,van der Vaart,&Ventura,2000),而原假设成立时,检验的p值应服从均匀分布,这就导致使用PPP值进行假设检验时一类错误率会低于设定的显著性水平,相应的PPMC方法的统计检验力也会受到影响。

2.3 基于有限信息的项目拟合统计量

由于传统的卡方类统计量都是建立在被试所有可能的作答反应模式基础上的,因此这类统计量又称作完全信息的拟合检验统计量。基于有限信息的拟合检验方法(Reiser,1996;Reiser&Lin,1999)则可以在较大程度上解决基于完全信息的统计量无法应用于CDM拟合检验的困境。

和基于完全信息的拟合检验不同,有限信息拟合检验利用的是完全列联表中的概括性信息,即使用完全列联表中的低阶信息评价模型数据拟合。具体来说,在CDM框架中,有限信息拟合检验通常使用题目对的双变量信息(Bivariate information)进行拟合检验,如此便可解决传统拟合检验的列联表稀疏问题。例如,使用传统的卡方统计量对一个30题的认知诊断测验进行拟合检验,列联表中可能的作答反应模式超过10亿种,而使用双变量信息可使作答反应模式的数量锐减至种。当然,除了双变量信息,有限信息拟合检验也可以基于更高阶的题目关联(例如基于三个题目之间的作答反应情况),但随着题目之间关联复杂性的提高,对有限信息统计量的解释也会更加复杂(Rupp etal.,2010)。下面具体介绍几种在CDM中可使用的项目有限信息拟合统计量。

2.3.1 基于题目对的对数发生比统计量

de la Torre和Douglas(2004)在提出高阶DINA模型时首次提出可以使用基于题目对之间的关联指标,即题目对的对数发生比,作为认知诊断项目拟合统计量。该统计量的思想近似于IRT框架中残差协方差的平均绝对差异统计量(M cDonald&Mok,1995)。令为观测数据中在题目j上得k分且在题目¢上得分的人数,为模型预测数据中在题目j上得k分且在题目上得分的人数,且,观测数据样本量为N,预测数据样本量为,通过计算观测数据和预测数据中题目j和题目j¢的对数发生比的绝对差异便可评价项目拟合。该统计量表达式如下：

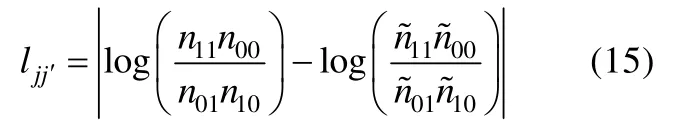
对于题目j而言,可以计算其与测验中其它所有题目之间的的均值用于项目拟合检验(de la Torre&Douglas,2004),的均值越接近0,模型对题目j拟合越好。然而,该检验方法无法获得检验的经验p值,因此Tem p lin和Henson(2006)以及 Chen,de la Torre和 Zhang(2013)提出可以将该统计量与蒙特卡洛重复抽样方法结合,计算题目对对数发生比的均方根误差或标准误及相应的经验p值用于测验的绝对拟合检验,其中均方根误差表达式为：,标准误表达式为：。

2.3.2 基于题目对相关统计量

该统计量通过计算题目两两之间的皮尔逊相关获得(DiBello,Roussos,&Stout,2007)。令分别为题目j在观测数据和期望数据中的作答反应向量,N和分别为观测数据和预测数据的样本量,则可以通过度量观测数据和期望数据中题目对相关的差异进行拟合检验,该统计量表达式如下：

2.3.3 基于题目对的Cohen’sk统计量

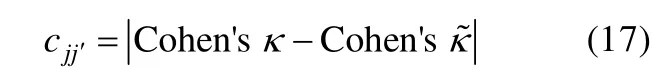
2.3.4 基于单题正确作答比例的统计量

以上各个统计量都是基于题目对的信息,而基于单题正确作答比例的统计量使用的是单个题目的信息,度量的是观测数据和预测数据中单个题目正确作答比例的差异。令和分别为题目j在观测数据和期望数据中的作答反应向量,N和分别为观测数据和预测数据的样本量,则该统计量表达式如下：

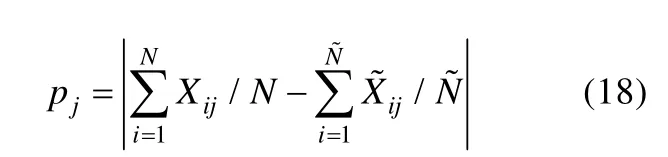
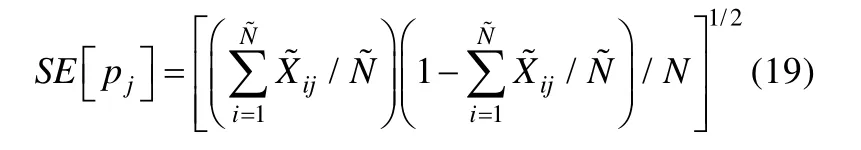
以上统计量既可以进行项目的绝对拟合检验,也可以对不同项目的拟合情况进行比较。由于这些统计量没有明确的理论分布,因此具有一定的局限性。此外,这些统计量也较难利用更高阶的边际信息。研究发现,进行相对拟合检验时,基于单题信息的统计量只能应对模型拟合差异较极端的情况,而当模型拟合较为相似时,基于题目对信息的统计量表现更好(de la Torre&Douglas,2008)。Chen等人(2013)的研究还发现,基于单题信息的统计量拟合检验力很差,几乎无法真正在实践中运用,而基于题目对相关和对数发生比的统计量在拟合检验性能上几乎没有差别。此外,基于题目对相关和对数发生比的统计量都无法侦查测验Q矩阵过度设定(即某些Q矩阵元素由“0”设定为“1”)的情况。

3 CDM总体绝对拟合检验统计量

CDM项目拟合统计量针对的是测验项目与数据的拟合情况,可用于对项目的选择。但在实践中,研究者和实践者需要明确选用何种认知诊断模型拟合数据,此时逐一进行项目拟合检验不现实也不合理。因此,CDM总体绝对拟合检验可以帮助研究者考察所选择模型与数据在总体上的绝对拟合情况,从而保证所选模型的适用性以及对被试诊断分类的准确性。

3.1 卡方类统计量

本文2.1部分介绍了用于CDM项目拟合检验的卡方类统计量,这些统计量是通过被试的属性掌握模式对被试进行分组的。卡方类统计量用于CDM总体拟合检验时则是通过被试的作答反应模式对被试进行分组的。然而前文提到,使用作答反应模式进行分组极易导致列联表稀疏问题,因此卡方类统计量基本无法用于CDM总体绝对拟合检验。

3.2 基于后验预测模型检查(PPMC)方法的统计量

大多数基于PPMC方法的统计量主要用于项目拟合检验,但可通过对部分PPMC方法的项目拟合检验统计量(如基于同分类的和基于总分的项目拟合统计量)进行加和用于模型的总体拟合检验。PPMC方法在上文已有详尽描述。此外,PPMC的差异度量检验一般会结合作图法一同使用。通过作图,将观测数据与模型预测数据直接呈现,可以直观展示观测数据和模型预测数据之间的差异(Gelman,Carlin,Stern,&Rubin,2003)。需注意的是,当样本量较大时,该方法显然会受到限制,但却可通过该方法考察数据中部分特定小样本的拟合情况(如高分组被试数据)(Sinharay,2006)。

3.3 基于有限信息的总体绝对拟合统计量

3.3.1 MAD统计量

Henson,Templin和Willse(2009)在提出LCDM(log-linear cognitive diagnosismodel)框架时提出可使用观测数据和模型预测数据所有项目对关联的绝对差异大小作为总体拟合检验指标。该统计量需在PPMC框架中获得,表达式为：

其中ijr为观测数据项目对关联,ˆijr为预测数据项目对关联。

3.3.2 M2统计量

前文介绍的用于CDM拟合检验的有限信息拟合统计量在实际使用中存在一定的缺陷,而Maydeu-Olivares和Joe(2005)提出的M r统计量可以有效避免其它有限信息拟合统计量的缺点,具有较大的扩展性。该类统计量仅用于测验的总体拟合检验。M r统计量可以利用任意的边际阶数信息,即任意数量的题目关联进行拟合检验,因此可作为有限信息拟合检验的一般性方法。M2统计量是M r统计量的一个特例,其利用的是两个题目组成的题目对信息。相关研究表明,使用M2统计量足以进行实际的有限信息拟合检验,且运算效率也较高(Cai,Maydeu-Olivares,Coffman,&Thissen,2006;Maydeu-Olivares&Joe,2005)。

M2统计量刻画的是观测的和期望的边际频数或边际概率之间的差异,因此需要将数据的完全信息缩减为二阶的边际信息,然后通过计算观测的和期望的二阶边际残差得到M2统计量。令O为每种作答反应模式中观测的人数比例向量,为每种作答反应模式中模型预测的人数比例向量,其中为模型参数的估计值,则二阶边际残差R2为：

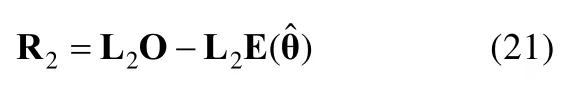
其中L2是一个维的算子矩阵,包含元素为0或1,用以将O和中的完全信息缩减为二阶边际信息。d为线性独立的一阶和二阶残差的数量(详见Maydeu-Olivares&Joe,2006)。得到R2后,通过权重矩阵W2,便可计算M2统计量：

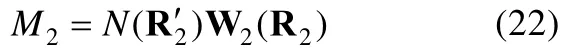
对M2统计量性能的研究大多是在IRT和结构方程模型框架下开展的(Maydeu-Olivares,Cai,&,2011;Maydeu-Olivares&,2013;Maydeu-Olivares&Joe,2005,2006),这些研究结果都有力证实了M2统计量良好的拟合检验性能。M2统计量在CDM中应用的研究却相对少见：Jurich(2014)通过一个小尺度的模拟研究检验M2统计量在LCDM框架中的统计性质,结果表明M2统计量在CDM框架中也具备对一类错误率良好的控制力,并且对模型的错误设定具有较高的检验力;Liu,Tian和Xin(2016)系统地检验了M2统计量在CDM中应用的性质,结果表明M2统计量在各种条件下都具备合适的一类错误率及良好的统计检验力,为M2统计量在CDM中的应用夯实了理论基础。

有限信息拟合检验方法的优点在于其能有效避免传统卡方检验的列联表稀疏问题,也无需通过重复抽样或MCMC算法进行大量耗时的计算,为实践提供了便利。此外,部分有限信息拟合统计量(如M2统计量)已在其它统计模型中进行了充分的应用,其拟合检验性能较为成熟。当然,有限信息拟合检验方法也存在一些缺点,比如早期在CDM中应用的统计量都难以进行绝对拟合检验,而M2统计量在CDM中的应用才刚刚起步,还需更多的模拟和实证研究进行进一步的探索。

4 CDM总体相对拟合检验统计量

相对拟合检验统计量在CDM拟合检验中应用较多。这类统计量基于模型资料的拟合情况以及模型本身的复杂度,可从多个备选模型中选择最优的模型。常见的CDM相对拟合检验统计量为基于信息量的统计量,考虑了模型的简洁性对数据解释的意义,对模型的复杂程度进行一定的惩罚。在认知诊断测验中,最为常用的相对拟合统计量为偏差(deviance,-2Log-Likelihood)、AIC(Akaike,1974)、BIC(Schwarz,1978)、DIC(Spiegelhalter,Best,Carlin,&van der Linde,2002)和贝叶斯因子(Bayes factor,Spiegelhalter&Sm ith,1982),这些统计量都没有绝对的拟合临界点。

4.1 偏差

偏差统计量是-2倍的似然函数值的自然对数,其值越小,表示模型拟合越好。其计算公式为(其中ML为似然函数)：

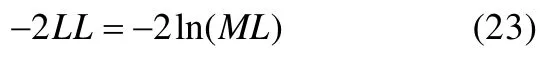
4.2 AIC和BIC

AIC(Akaike’s information criterion)和 BIC(Bayesian information criterion)可在偏差统计量的基础上获得,二者可用以下公式表示：

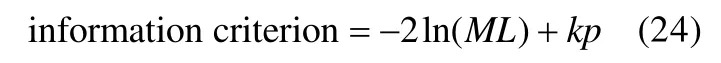
4.3 DIC

DIC通常用于贝叶斯框架中MCMC算法下的模型比较,是AIC的推广,同样包含模型拟合情况和模型复杂程度两个部分。其表达式如下：

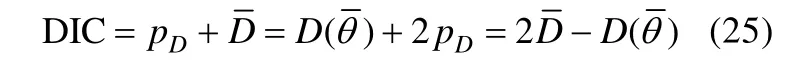
4.4 贝叶斯因子

贝叶斯因子通常用于在贝叶斯框架中两个非嵌套模型之间的比较。对于竞争模型M A和M B而言,贝叶斯因子计算的是二者边际似然的比值,表达式如下：

若BF＞1,则支持模型M A,否则支持模型MB。

大量关于CDM的模拟或应用研究都应用了上述统计量,这是由于在CDM绝对拟合统计量亟待开发的情况下,使用相对拟合统计量是较为可行的做法。然而,这些统计量在CDM中的检验效果也会因使用条件不同而存在些许差异。例如,使用MCMC算法时,DIC相比于AIC或BIC具备更优良的拟合检验性能(de la Torre&Douglas,2008)。由于BIC比AIC对模型自由参数的惩罚更加严格,因此当模型的错误设定针对模型参数项时,BIC相比于AIC对模型错误设定的侦查效果更差(Kunina-Habenicht et al.,2012)。此外,Galeshi和Skaggs(2014)的研究发现,当样本量较大时,AIC和BIC的拟合检验效果近似;而当样本量较小时,BIC的拟合检验效果更优越。

5 个人拟合检验方法

个人拟合检验用于考察所选模型是否适用于参加测验的被试。由于认知诊断评价需要对被试的属性掌握模式做出诊断分类,被试的作答反应如果和所选模型不符,就可能导致无效的诊断,因此个人拟合检验对于认知诊断评价来说尤为重要(Cui&Li,2015)。对于认知诊断实践而言,如果部分被试的作答反应不符合所选用模型的基本假定,或该部分被试的作答反应与大部分被试存在较大差异时,便要考虑将这部分被试的数据删除,否则就会影响模型的参数估计结果及对被试的诊断(宋丽红,2012)。若个人拟合检验的结果显示大部分被试都不拟合模型,则可能是所选用的模型在总体上对数据就不拟合,因而模型的总体拟合是个人拟合探测的基础。被试不拟合的原因可能来自三个方面：首先是所选模型的假设无法准确刻画被试的作答反应模式;其次是被试出现了异常作答,例如作弊、对题干进行反常或过度理解、随机作答等(Cui&Leighton,2009);最后是测验的Q矩阵存在错误设定,例如被试作答所使用的认知属性未被包含在Q矩阵当中(Liu,Douglas,&Henson,2009)。当前,个人拟合统计量的开发主要还是在IRT框架中进行(详见Rupp,2013),而在CDM框架下开发的个人拟合统计量却相对较少。以下部分介绍几种已经在CDM框架中使用的个人拟合统计量。

5.1 被试误差均方根

Yan等人(2003)较早提出使用被试误差均方根评价个人拟合,和使用项目误差均方根检验项目拟合类似,使用该统计量需要在PPMC方法下进行。定义观测数据中被试i在项目上 的 作 答 反 应 为为在MCMC算法第t次迭代中出现该作答反应的期望概率,则观测数据xij在第t次迭代中的平方误差为。此时可使用被试i在第t次迭代中的误差均方根作为被试拟合的差异度量：

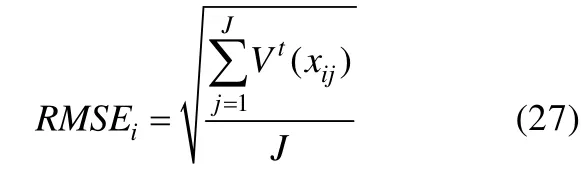
同理,在预测数据中,对被试i同样可以计算其差异度量,最后使用在所有迭代中的比例作为个人拟合好坏的指标,当该比例接近0.5时说明个人拟合较好。然而,该指标是在PPMC框架下运用的,依赖于特定的算法,在实际研究中使用具有一定的局限性。

5.2 层级一致性指标

层级一致性指标(the hierarchy consistency index,HCI;Cui&Leighton,2009)是基于属性层级模型(the attribute hierarchy method,AHM;Leighton,Gierl,&Hunka,2004)建立的个人拟合统计量。属性层级模型事先假定测验所考察的认知属性之间具有属性层级关系,并且强调测验编制要在属性层级关系的指导下进行。在属性层级关系的假设下,被试如果答对了测量复杂属性的题目,那么他们也理应答对测量简单属性的题目。因此,构建HCI的基本思想便是衡量被试的真实作答反应模式与属性层级关系作用下的期望作答反应模式之间的匹配程度。HCI的表达式如下：

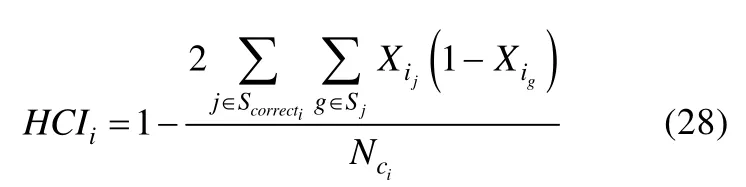
Cui和 Leighton(2009)通过模拟研究发现,HCI对个人不拟合的侦查效果会受到不拟合类型、项目区分力(item discrim inating power)和测验长度的影响,尤其是当测验项目的区分力都较高时,HCI的检验力才会达到最大。值得注意的是,使用HCI进行个人拟合检验的前提是测验所考察属性的层级关系已被正确界定,然而实践中属性层级关系的界定一般是通过领域专家完成的,由于专家的知识经验难免存在差异,因此界定的属性层级关系不可能保证完全准确,此时使用HCI进行拟合检验得到的不拟合结果便可能源于Q矩阵的错误设定。更重要的是,当测验的属性之间不涉及层级关系或者仅有部分属性之间存在层级关系,HCI便失去了检验效力,因此HCI的这种计算方法对不拟合的评估方式存在一定的局限性。

5.3 似然比检验统计量

Liu等人(2009)通过对假设的反常作答反应模式似然值和正常的作答反应模式似然值进行对比,提出了用于鉴别具有反常作答反应倾向被试的似然比检验统计量。为了得到假设的反常作答反应模式的似然值,相应的认知诊断模型的项目反应函数需要进行如下修改：

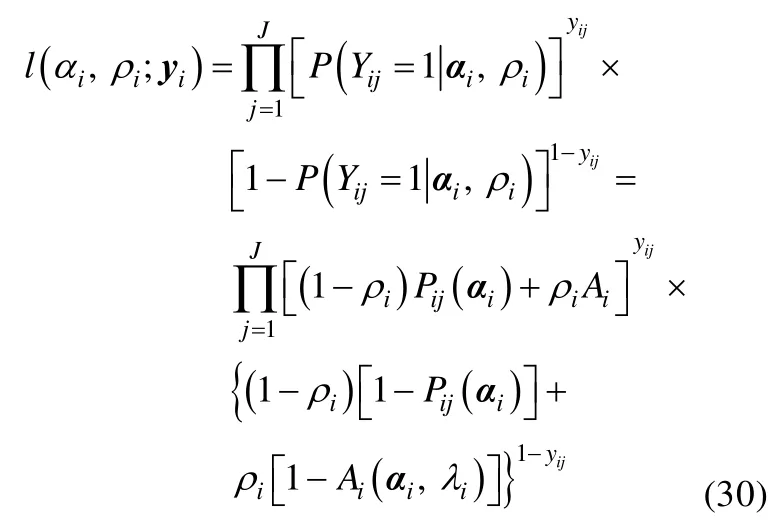
边际似然表达式为：

其中l0或L0对应的是被试正常作答的假设,而lA或LA对应的是被试反常作答的假设。

Liu等人(2009)通过模拟研究发现,当测验较长或被试反常作答倾向较明显时,似然比检验统计量对被试失拟的统计检验力较高。此外,在DINA模型框架下,使用基于边际似然的T2统计量比使用基于联合似然的T1统计量更加可靠。尽管此类统计量能够鉴别出被试的反常作答反应倾向,但其缺点在于：此类统计量只定义了两种失拟类型,即“不合逻辑的高得分”和“不合逻辑的低得分”两种情况,而被试的反常作答反应可能包含多种形式,被试失拟的来源也较复杂,所以此类统计量对于其它失拟类型的检验程序和检验效果还有待研究。

5.4 lz统计量

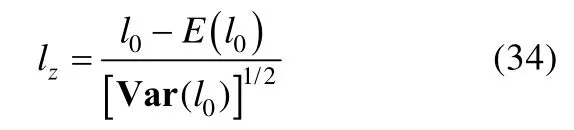
Cui和Li(2015)通过模拟研究发现,在项目区分力较高的情形下,lz统计量在认知诊断框架中也呈现渐进的正态分布。

5.5 反应一致性指标

反应一致性指标(the response conform ity index,RCI;Cui&Li,2015)的基本思想是：Q矩阵无法对每一个被试作答所使用的属性进行界定,这就可能导致被试的实际作答反应和Q矩阵预测的作答反应不符,因此RCI用于检验被试实际作答反应和Q矩阵预测的作答反应之间的一致性。该统计量表达式如下：

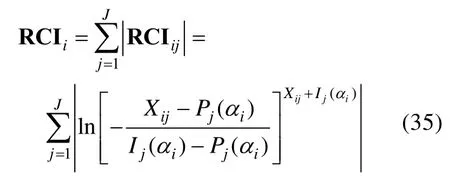
其中ia是被试i的属性掌握模式,为在ia影响下模型估计的正确作答题目j的概率。表示属性掌握模式为ia的被试对题目j的理想反应,其值为0或1,当被试掌握了题目所要求的所有属性时,,如果被试未掌握全部题目所要求的属性,则。

Cui和 Li(2015)使用 C-RUM(compensatory RUM)模型通过模拟研究系统地比较了T2、lz和RCI统计量的拟合表现。研究结果表明,当题目数量较多或者题目区分力较大时,这三个统计量都具有较高的统计检验力;T2统计量在各模拟条件下都呈现出了膨胀的一类错误率,而lz和RCI统计量的一类错误率都接近理论假设。

6 小结和展望

由于认知诊断理论是新一代的心理教育测量理论,对认知诊断理论各个方面的探讨都还处于发展阶段,而认知诊断模型资料拟合检验作为提供认知诊断评价效度证据的重要方面,更应置于重要的研究地位。近20多年来,随着认知诊断理论的日趋完善,不少的研究者提出了相应的认知诊断拟合统计量。本文在已有研究的基础上,详尽了可实际应用的认知诊断拟合检验统计量及相关研究,试图为未来研究者提供一个整体的框架,以期对认知诊断研究的进一步完善。以下通过一个表格对现有主要的CDM拟合检验研究进行总结(见表1)。

CDM拟合检验面临的困境主要在于认知诊断数据的稀疏性问题,相关的拟合检验方法或统计量都围绕于此试图加以解决。传统卡方类统计量尽管最为认知诊断拟合检验所诟病,但由于计算的简便性和易理解性,还是值得未来的研究者继续借鉴卡方统计量的思想进行改造,并结合新的途径以实现新的突破,例如统计量在EM算法或PPMC方法下都具有较好的拟合效果(Wang etal.,2015)。PPMC方法通过后验预测分布解决参数估计不准确问题,能够实现小样本情形下的拟合检验(Wang et al.,2015)。尽管在早期的认知诊断拟合检验中PPMC方法应用较多,但所提出的统计量大多都仅仅是一个差异的度量,各统计量分布情况不明确,无法可靠地进行拟合检验,还需未来研究进一步完善。但相比传统卡方类统计量,PPMC方法理应是一个更加优越的拟合检验方法。有限信息拟合检验是最新发展的CDM拟合检验方法。有限信息拟合统计量,尤其是M2统计量的优越性能已在IRT和结构方程模型框架中得到了充分的证明。尽管在CDM框架中有限信息拟合统计量应用较少,但根据有限信息拟合检验的基本思想和已有研究结论,不难发现有限信息拟合检验方法对CDM拟合检验具有不俗的表现,是值得未来研究的CDM拟合检验领域。

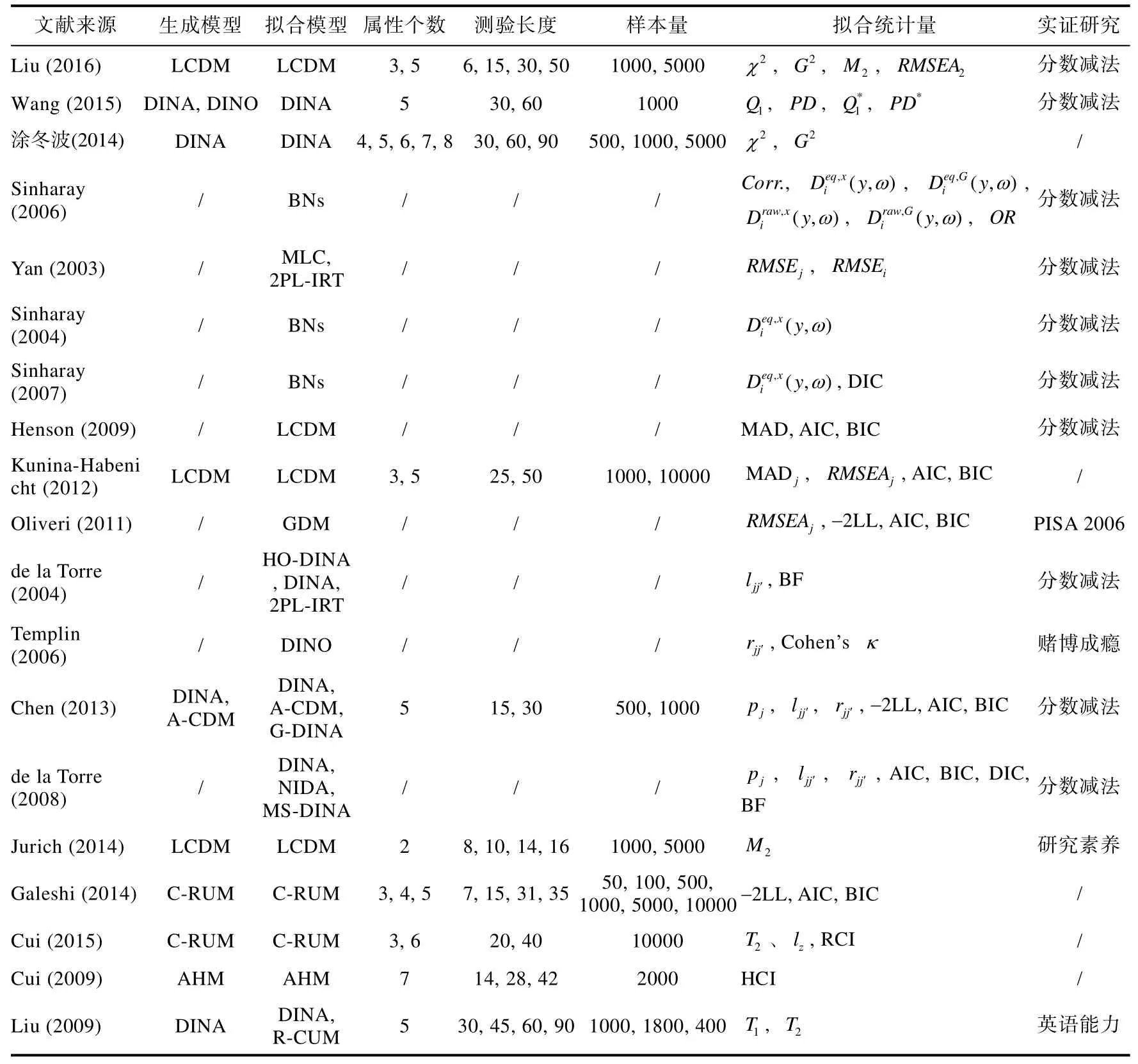
表1 认知诊断模型资料拟合检验研究总结

本文针对实践中如何选用合适的CDM拟合统计量给出如下建议。针对项目拟合检验,只有当样本量足够大且题目数量很少时,可考虑使用等卡方类统计量。而对于一般的认知诊断测验,应尽量避免使用卡方类统计量。如果模型的参数估计使用MCMC算法,可优先考虑使用基于PPMC方法的统计量,例如平均绝对差异及其RMSEA。而当模型的参数估计方法不限定于MCMC时,建议使用基于双变量信息的有限信息拟合统计量。针对总体的绝对拟合检验,根据Liu等(2016)的研究结论,M2统计量的性能良好且稳定,可成为在各种条件下的优先选择。针对个人拟合检验,可根据不同个人拟合检验统计量的检验逻辑进行选择,不同统计量之间不存在绝对的优劣。例如当属性存在层级关系时,则优先选择HCI。而根据Cui和Li(2015)的研究结论,RCI更适用于在被试创造性作答、猜测作答、被试瞌睡和Q矩阵错误设定情形下的被试失拟检验,而lz对被试疲劳导致的被试失拟检验效果更好。

尤需注意的是,认知诊断测验的开发以及对被试的诊断评价都是在Q矩阵的指导下进行的。现有的CDM拟合检验方法都假定Q矩阵的界定是正确的,而错误的Q矩阵对认知诊断的参数估计和被试分类都存在影响(Rupp&Templin,2008),因此Q矩阵的正确性对拟合检验效果自然起到了先导性和决定性的作用。然而,Q矩阵的正确界定也是认知诊断实践面临的重大挑战,最突出的例子便是20多年来研究者对Tatsuoka(1990)的分数减法数据的Q矩阵界定争议不断,至今未有定论。因此,为了使现有的CDM拟合检验方法能更加准确和有效地运用,如何更好地正确界定Q矩阵需要未来研究更多深入的探讨。

对于未来研究的开展,本文提出以下几点研究方向的展望。

第一,现有的大部分拟合统计量性能研究都是基于DINA、C-RUM等特定模型开展的,未来的研究可以探讨各统计量在其它模型或者一般化模型下的拟合检验性能;

第二,现有的拟合统计量开发都是基于0、1计分的CDM进行的,而CDM也可进行多级计分或包含多级属性,未来的研究可以进一步探讨不同的拟合检验方法或统计量如何在多级数据或多级属性下拓展;

第三,现有的拟合统计量性能大多未被充分证明,未来的研究可以进一步通过模拟研究检验各统计量在一类错误率和统计检验力上的表现,并且丰富研究条件,使各统计量性能更加明确。

刘永,涂冬波.(2015).认知诊断测验Q矩阵估计方法比较.中国考试,(5),53–63.

单昕彤,谭辉晔,刘永,吴方文,涂冬波.(2014).项目反应理论中模型—资料拟合检验常用统计量.心理科学进展,22,1350–1362.

宋丽红.(2012).DINA改进模型(R-DINA)的提出及三个诊断模型自动选择机制研究(博士学位论文).江西师范大学,南昌.

涂冬波,张心,蔡艳,戴海琦.(2014).认知诊断模型-资料拟合检验统计量及其性能.心理科学,37,205–211.

辛涛,乐美玲,张佳慧.(2012).教育测量理论新进展及发展趋势.中国考试,(5),3–11.

Agresti,A.,&Finlay,B.(1997).Statisticalmethods for the social sciences(3rd ed.,p.258).Upper Sadd le River,NJ:Prentice Hall.

Akaike,H.(1974).A new look at the statistical model identification.IEEE Transactions on Automatic Contro l,19(6),716–723.

Bartholomew,D.J.,&Tzamourani,P.(1999).The goodness of fit of latent trait models in attitude measurement.Socio logical Methods&Research,27,525–546.

Cai,L.,Maydeu-Olivares,A.,Coffman,D.L.,&Thissen,D.(2006).Lim ited-information goodness-of-fit testing of item response theory models for sparse 2Ptables.British Journal of Mathematical and Statistical Psycho logy,59,173–194.

Chen,J.S.,de la Torre,J.,&Zhang,Z.(2013).Relative and absolute fit evaluation in cognitive diagnosis modeling.Journal ofEducational Measurement,50,123–140.

Chen,W.H.,&Thissen,D.(1997).Local dependence indexes for item pairs using item response theory.Journal ofEducational and Behavioral Statistics,22,265–289.

Cui,Y.(2007).The hierarchy consistency index:Development and analysis(Unpublished doctoral dissertation).University of Alberta,Edmonton,A lberta,Canada.

Cui,Y.,&Leighton,J.P.(2009).The hierarchy consistency index:Evaluating person fit for cognitive diagnostic assessment.Journal of Educational M easurement,46,429–449.

Cui,Y.,&Li,J.(2015).Evaluating person fit for cognitive diagnostic assessment.Applied Psychological Measurement,39,223–238.

de la Torre,J.,&Douglas,J.A.(2004).Higher-order latent trait models for cognitive diagnosis.Psychometrika,69,333–353.

de la Torre,J.,&Douglas,J.A.(2008).Model evaluation and multip le strategies in cognitive diagnosis:An analysis of fraction subtraction data.Psychometrika,73,595–624.

DiBello,L.V.,Roussos,L.A.,&Stout,W.F.(2006).Review of cognitively diagnostic assessment and a summary of psychometric models.In C.R.Rao&S.Sinharay(Eds.),Handbookofstatistics(Vol. 26, pp. 979–1030).Am sterdam:Elsevier.

D rasgow,F.,Levine,M.V.,&W illiam s,E.A.(1985).Appropriateness measurement w ith polychotomous item responsemodels and standardized indices.British Journal ofMathematical and Statistical Psycho logy,38,67–86.

Embretson,S.E.(1998).A cognitive design system approach to generating valid tests:Application to abstract reasoning.PsychologicalMethods,3,380–396.

Galeshi,R.,&Skaggs,G.(2014).Traditional fit indices utility in new psychometric model:Cognitive diagnostic model.International Journal of Quantitative Research in Education,2,113–132.

Gelman,A.,Carlin,J.B.,Stern,H.S.,&Rubin,D.B.(2003).Bayesian data analysis(2nd ed.).New York:Chapman&Hall.

Henson,R.,Roussos,L.,Douglas,J.,&He,X.M.(2008).Cognitive diagnostic attribute-level discrim ination indices.Applied Psychological Measurement,32,275–288.

Henson,R.A.,Templin,J.L.,&Willse,J.T.(2009).Defining a fam ily of cognitive diagnosis models using log-linear models w ith latent variables.Psychometrika,74,191–210.

Jurich,D.P.(2014).Assessing model fit ofmultidimensional item response theory and diagnostic classification models usinglim ited-informationstatistics(Unpublished doctorial dissertation). James M adison University,Harrisonburg,Virginia,United States.

Kunina-Habenicht,O.,Rupp,A.A.,&W ilhelm,O.(2012).The im pact of model m isspecification on parameter estimation and item-fit assessment in log-linear diagnostic classification models.Journal of Educational Measurement,49,59–81.

Leighton,J.,& Gierl,M.(2007).Cognitive diagnostic assessment for education:Theory and applications.New York:Cambridge University Press.

Leighton,J.P.,Gierl,M.J.,&Hunka,S.M.(2004).The attribute hierarchy method for cognitive assessment:A variation on Tatsuoka’s rule-space approach.Journal of Educational Measurement,41,205–237.

Levy,R.,M islevy,R.J.,&Sinharay,S.(2009).Posterior predictivemodel checking formultidimensionality in item response theory.Applied Psycho logical Measurement,33,519–537.

Liu,Y.,Douglas,J.A.,&Henson,R.A.(2009).Testing person fit in cognitive diagnosis.Applied Psychological Measurement,33,579–598.

Liu,Y.L.,Tian,W.,&Xin,T.(2016).An application ofM 2statistic to evaluate the fit of cognitive diagnostic models.Journal of Educational and Behavioral Statistics,41(1),3–26.

Lord,F.M.(1980).Applications of item response theory to practical testingproblems.Hillsdale,NJ:Law rence Erlbaum Associates.

Maydeu-O livares,A.,Cai,L.,& Hernández,A.(2011).Comparing the fit of item response theory and factor analysis models.StructuralEquationModeling:A Multidisciplinary Journal,18,333–356.

Maydeu-Olivares,A.,& Joe,H.(2005).Lim ited-and full-information estimation and goodness-of-fit testing in 2ncontingency tables:A unified framew ork.Journal of the American Statistical Association,100,1009–1020.

Maydeu-O livares,A.,&Joe,H.(2006).Lim ited information goodness-of-fit testing in multidimensional contingency tables.Psychometrika,71,713–732.

Maydeu-O livares,A.,&Montaño,R.(2013).How should we assess the fit of Rasch-type models?Approximating the pow er of goodness-of-fit statistics in categorical data analysis.Psychometrika,78,116–133.

M cDonald,R.P.,&Mok,M.M.-C.(1995).Goodness of fit in item response models.Multivariate Behavioral Research,30,23–40.

Oliveri,M.E.,&von Davier,M.(2011).Investigation of model fit and score scale comparability in international assessments.Psychological Testand AssessmentModeling,53,315–333.

Read,T.R.C.,&Cressie,N.A.C.(1988).Goodness-of-fit statistics for discrete multivariate data.New York,NY:Springer.

Reiser,M.(1996).Analysis of residuals for the multionm ial item responsemodel.Psychometrika,61,509–528.

Reiser,M.,&Lin,Y.C.(1999).A goodness-of-fit test for the latent class model w hen expected frequencies are small.Socio logical Methodo logy,29,81–111.

Robins,J.M.,van der Vaart,A.,&Ventura,V.(2000).Asymptotic distribution of P values in com posite null models.Journal of the American Statistical Association,95,1143–1156.

Rubin,D.B.(1984).Bayesianly justifiable and relevant frequency calculations for the applied statistician.The Annals ofStatistics,12,1151–1172.

Rupp,A.A.(2013).A systematic review of themethodology for person fit research in item response theory:Lessons about generalizability of inferences from the design of simulation studies.Psychological Test and Assessment Modeling,55,3–38.

Rupp,A.A.,& Tem plin,J.L.(2008).The effects of Q-matrix m isspecification on parameter estimates and classification accuracy in the DINA model.Educational and Psycho logical Measurement,68,78–96.

Rupp,A.A.,Temp lin,J.,&Henson,R.A.(2010).Diagnostic measurement:Theory,methods,and applications.New York:Guilford.

Schwarz,G.(1978).Estimating the dimension of a model.Annals ofStatistics,6(2),461–464.

Sinharay,S.(2005).Assessing fit of unidimensional item response theory models using a Bayesian approach.Journal ofEducational Measurement,42,375–394.

Sinharay,S.(2006). M odel diagnostics for Bayesian netw orks.JournalofEducationalandBehavioral Statistics,31,1–33.

Sinharay,S.,A lmond,R.,&Yan,D.L.(2004).Assessing fit ofmodels with discrete proficiency variables in educational assessment(ETSRR-04-07).Princeton NJ:ETS.

Sinharay,S.,&A lmond,R.G.(2007).Assessing fit of cognitive diagnostic models:A case study.Educational and Psychological Measurement,67,239–257.

Sinharay,S.,&Johnson,M.S.(2003).Simulation studies applyingposteriorpredictivemodelcheckingfor assessing fit of the common item response theory models(ETSRR-03-28).Princeton,NJ:ETS.

Spiegelhalter,D.J.,&Sm ith,A.F.M.(1982).Bayes factors for linear and log-linear models w ith vague prior information.Journal of the Royal Statistical Society:Series B,44,377–387.

Spiegelhalter,D.J.,Best,N.G.,Carlin,B.P.,&van der Linde,A.(2002).Bayesian measures ofmodel com plexity and fit.Journal of the Royal Statistical Society:Series B,64,583–639.

Stone,C.A.(2000).Monte carlo based null distribution for an alternative goodness-of-fit test statistic in IRT models.Journal ofEducational Measurement,37,58–75.

Tatsuoka,K.K.(1983).Rule space:An approach for dealing w ith m isconceptions based on item response theory.Journal ofEducational Measurement,20,345–354.

Tatsuoka, K. K. (1990). Toward an integration of item-response theory and cognitive error diagnosis.In N.Frederiksen,R.G laser,A.Lesgold,&M.G.Shafto(Eds.),Diagnostic monitoring of skill and know ledge acquisition(pp.453–488).Hillsdale,NJ:Law rence Erlbaum.

Tem plin,J.L.,&Henson,R.A.(2006).Measurement of psychological disorders using cognitive diagnosis models.Psycho logical Methods,11,287–305.

Tollenaar,N.,&M ooijaart,A.(2003).Type I errors and power of the parametric bootstrap goodness-of-fit test:Full and lim ited information.BritishJournalof Mathematical and Statistical Psychology,56,271–288.

Wang,C.J.,& Gierl,M.J.(2007).Investigating the cognitive attributes underlying student performance on the SAT®critical reading subtest:an application of the attribute hierarchy method.Paper presented at the 2007 annual meeting of the National Council on Measurement in Education.

Wang,C.,Shu,Z.,Shang,Z.R.,&Xu,G.J.(2015).Assessing item-level fit for the DINA model.Applied Psycho logical Measurement,39,525–538.

Yan,D.L.,M islevy,R.J.,&A lmond,R.G.(2003).Design and analysis in a cognitive assessment(ETS RR-03-32).Princeton NJ:ETS.

Yen,W.M.(1981).Using simulation results to choose a latent traitmodel.Applied Psycho logical Measurement,5,245–262.