Positive Solu tions of Non linear Ellip tic Prob lem in a Non-Sm ooth Planar Dom ain
2014-05-13BENBOUBAKERMohamedAmine
BEN BOUBAKERM oham ed Am ine
Institut Preparatoire aux Etudes D’Ing´enieur De Nabeul University of Carthage CampusUniversitaireM erezka,8000,Nabeul,Tunisia.
Positive Solu tions of Non linear Ellip tic Prob lem in a Non-Sm ooth Planar Dom ain
BEN BOUBAKERM oham ed Am ine∗
Institut Preparatoire aux Etudes D’Ing´enieur De Nabeul University of Carthage CampusUniversitaireM erezka,8000,Nabeul,Tunisia.
Received 2Decem ber 2013;A ccep ted 28 June 2014
. Wef indandprove3Ginequal i t ies for theLaplacianGreenfunct ionwi th the D irich let boundary cond ition,w hich are app lied to show the existence of positive continuous solutions of the non linear equation w here V and g are Borelm easurable functions,required to satisfy suitable assum ptions related to a new functional class J.Our app roach uses the Schauder fixed point theorem.
Greenfunct ion;Schauder f ixedpoint theorem;superharmonicfunct ion.
1 In troduction
In this paper,w e w ork in the Euclidean space R2.By Sα,w e denote the dom ain defined by
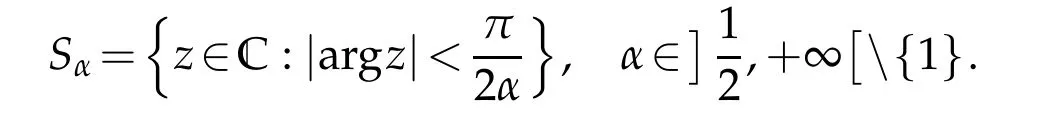
The objective is to study the existence of con tinuous solu tions for the non linear ellip tic p roblem
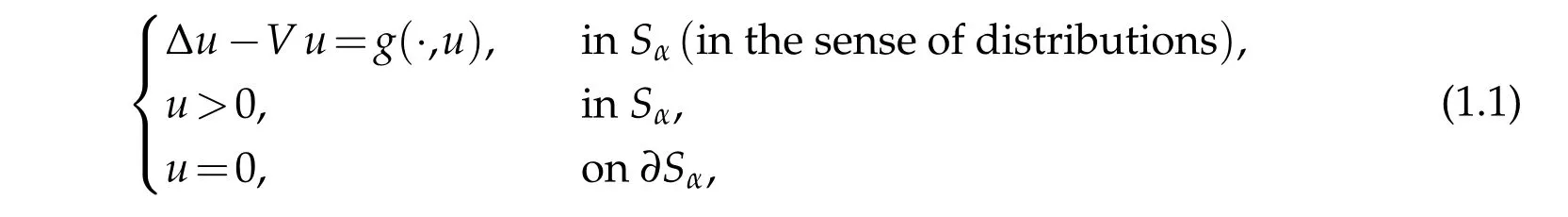
w here V and g are Borelm easu rable functions,required to satisfy suitable assum p tions related to a new functional class J.The existence resu lts of p roblem(1.1)have been extensively stud ied w hen V=0 and the special non linearity g(x,t)=p(x)q(t),for both bounded and unbounded dom ain D in(n≥1),w ith sm ooth com pact boundary(see for exam p le[1–4]).On the other hand,in[5–7],the au thors considered the p roblem(1.1) w here there isno restrictionson the sign of g,and D isan unbounded dom ain in(n≥1) w ith a com pact Lipschitz boundary.Then,they p roved the existence of infinitely m any solu tionsp rovided that g is in a certain Kato class.Nam ely,they show ed that there exists a num ber b0>0 such that for each b∈(0,b0],there existsa positive continuous solution u insatisfying

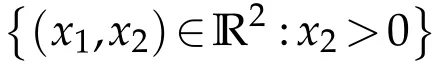
Theorem1.1.(3G-Theorem)There existsa constant C1=C1(α)>0 such that forall x,y and z in Sα,wehave

whereδ(x)is the Euclidean distance from x to∂Sα.
Thisenablesus to define and study,in Section 4 a new Kato class J of functionson Sα. Let

Definition1.1.Wesay that a Borelmeasurable function q on Sαbelongs to the Kato class Jifq satisfies thefollow ing conditions:

Note that ifα=1,then J is the Kato class K in troduced and stud ied in[8].For a Borel m easurable function q on Sα,let
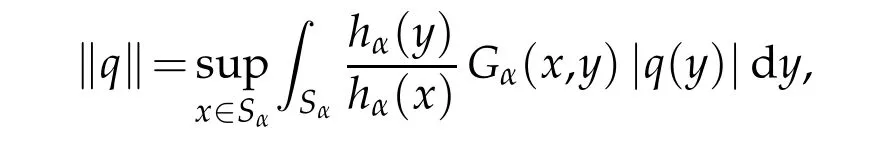
w here hα(x)=|x|αcos(αarg x),for all x∈Sα.To study the p roblem(1.1)in section 5,w e assum e the follow ing cond ition on V and g:
(H1)The function g is a Borelm easu rable on Sα×(0,∞),continuousw ith respect to the second variable and satisfies
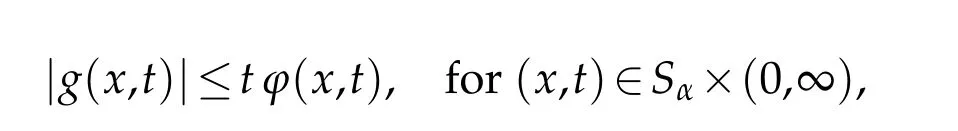
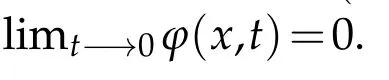
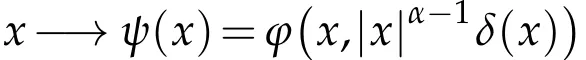
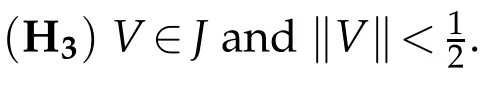
Ourm ain resu lt is the follow ing:
Theorem1.2.Assume(H1)-(H3).Then the problem(1.1)has infinitelymany continuous solutions.M oreprecisely,there existsε0>0 such thatforeachε∈(0,ε0],thereexistsa solution u of
(1.1),continuouson Sαand satisfying

The follow ing notionsw illbe adop ted:
i)Let f and k be tw o positive functionson a setΩ.We say that f is com parable to k onΩand w e denote fk,if there exists C>1,such that∀x∈Ω.
iii)B(x,r)denotes the Euclidean open ballof center x and rad ius r.
Throughout this paper,C denotes a generic positive constantw hichm ay vary from line to line andΩcdenotes the com p lem entary ofΩin.
2 Inequalities for the G reen function
Proposition2.1.([10])There existsa constant Cα>0,such that forall x and y in Sα,wehave
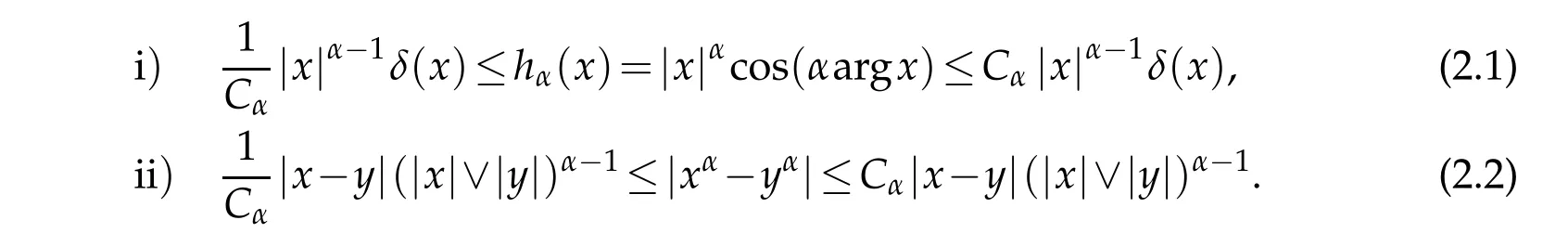
Theorem2.1.([10])Letα∈]0,+∞[{1}.Then,forall x,y∈Sα

Lemma2.1.ThereexistsC=C(α)>1,such thatforallx,y∈Sα,wehave thefollow ing properties:

Proof.i)Assum e|x|α-1δ(x)|y|α-1δ(y)≤|x-y|2(|x|∨|y|)2(α-1).Let Cαbe the constant defined in Proposition2.1 and x,y∈Sα.Let
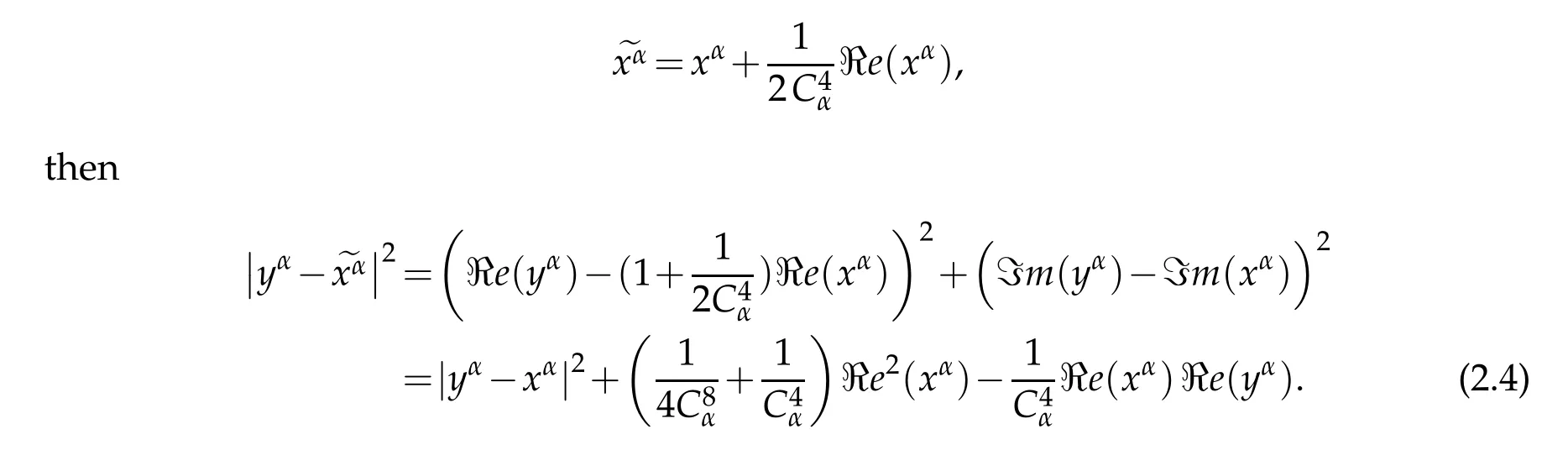
Since|x|α-1δ(x)|y|α-1δ(y)≤|x-y|2(|x|∨|y|)2(α-1),it follow s,by Proposition2.1,that

Thus,w e deduce that
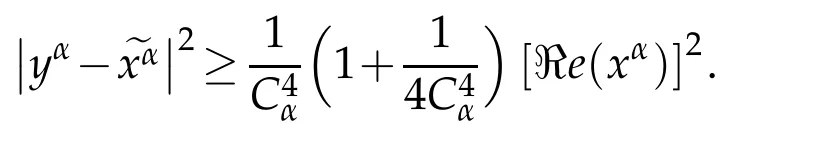
Using Proposition 2.1,w e get
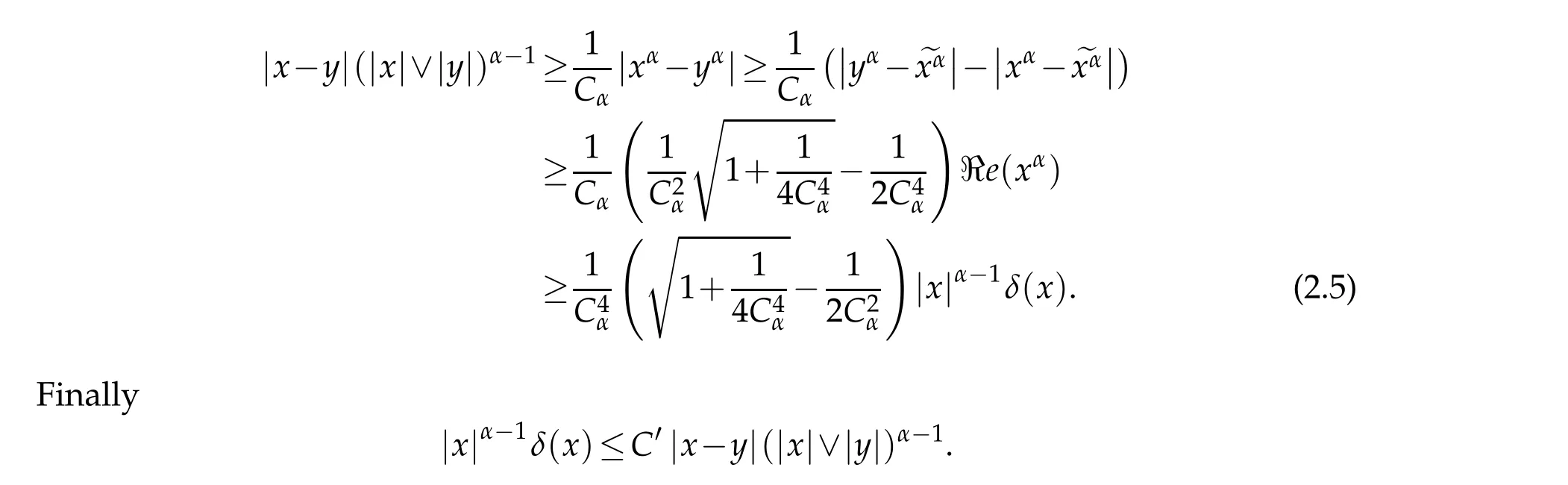
By interchanging the role of x and y,w e obtain(i).
ii)Assum e|x-y|2(|x|∨|y|)2(α-1)≤|x|α-1δ(x)|y|α-1δ(y),then,by Proposition 2.1,w e get
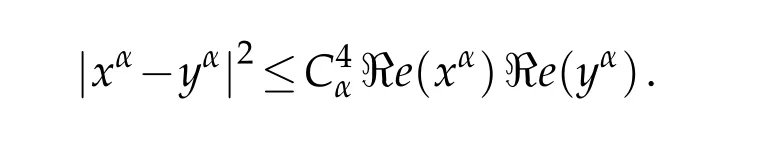
In consequence,w e obtain
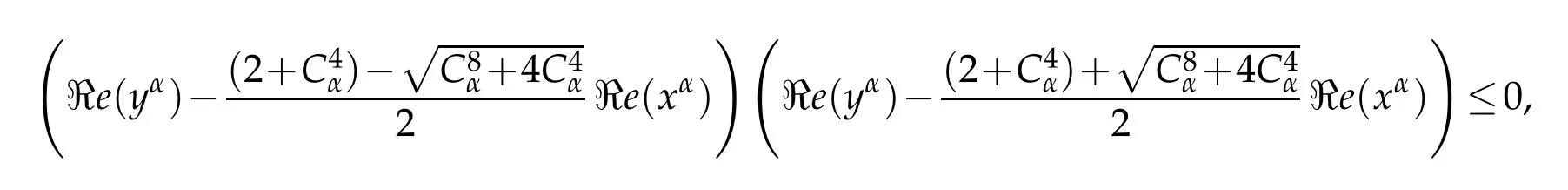
w hich gives
So,by using Proposition 2.1,w e deduce that

The p roof is com p lete.
Proposition2.2.Thereexists C=C(α)>0 depending only on Sα,such that forall x,y in Sα
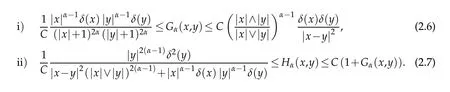
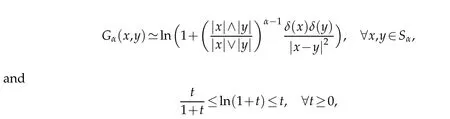
there exists C>0 such that

Since|xα-yα|≃|x-y|(|x|∨|y|)α-1andδ(x)≤|x|,there exists C>0 such that

ii)The left hand side inequality in(2.7)follow s from(2.8).We p rove the righ t hand side inequality.There are tw o cases to d iscuss:
If|x|α-1δ(x)|y|α-1δ(y)≤|x-y|2(|x|∨|y|)2(α-1),then it follow s by Lemm a 2.1 that
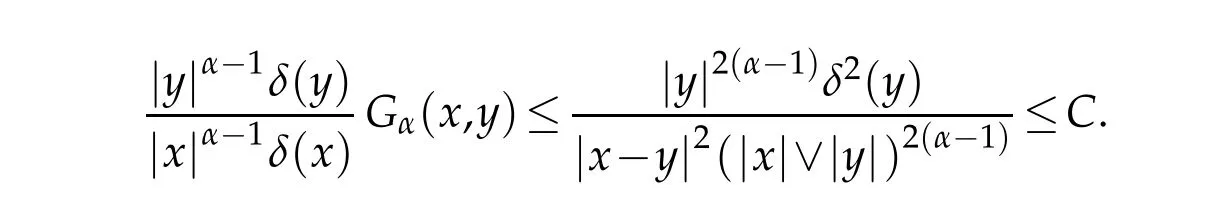
If|x|α-1δ(x)|y|α-1δ(y)≥|x-y|2(|x|∨|y|)2(α-1),then it follow s by Lemm a 2.1 that
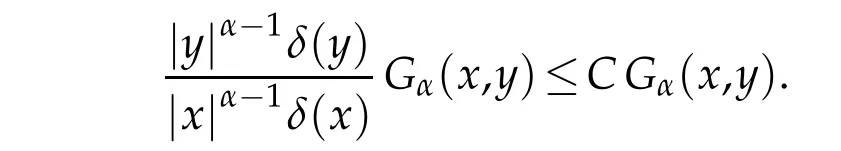
The p roof is com p lete.
ProofofTheorem1.1.Since the function z7-→zαis a con form alm app ing from Sαinto the half p lane S1.It follow s from 3G inequality p roved in[8]that,for all x,y and z in Sα
将需要反向计分的条目进行转换后,所有被试的数据根据量表总得分由高到低进行排列,以总得分前27%的被试作为高分组,后27%的被试作为低分组,两组被试每一条目得分的平均数差异均显著,ps<0.01。被试每一条目得分与量表总得分之间均呈显著正相关,相关系数在0.35~0.87之间。
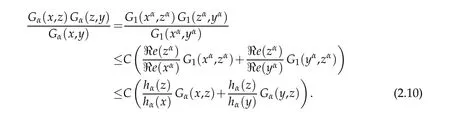
Thus the resu lt follow s from Proposition 2.1.
3 Kato class
Proposition3.1.Let R>0,then forall x,y∈Sα∩B(0,R),wehave
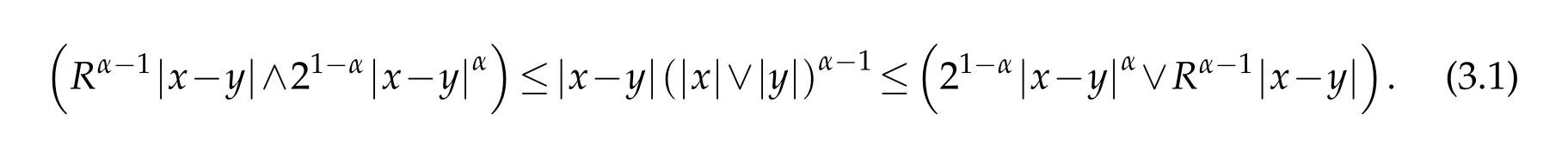
Proof.We can suppose that|x|≥|y|.Assum e12<α<1,then

Assum eα>1,then

The p roof is com p lete.
Proposition3.2.Letq bea Borelmeasurablefunction on Sαsuch thatq∈J,then foreach R>0,

Proof.By(2.7)w e have
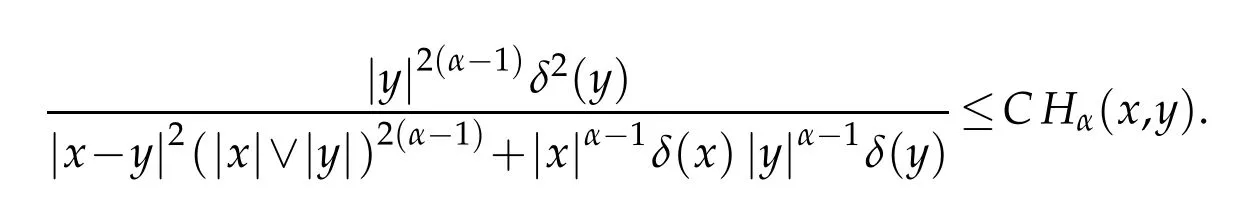
This im p lies by Proposition 2.1,that for all x,y∈Sα
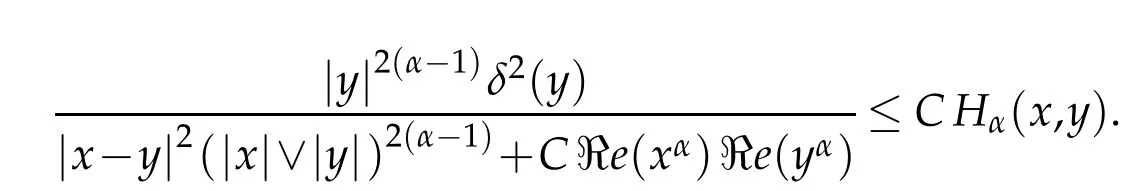


Since q∈J,then by(1.3)there exists r>0 such that
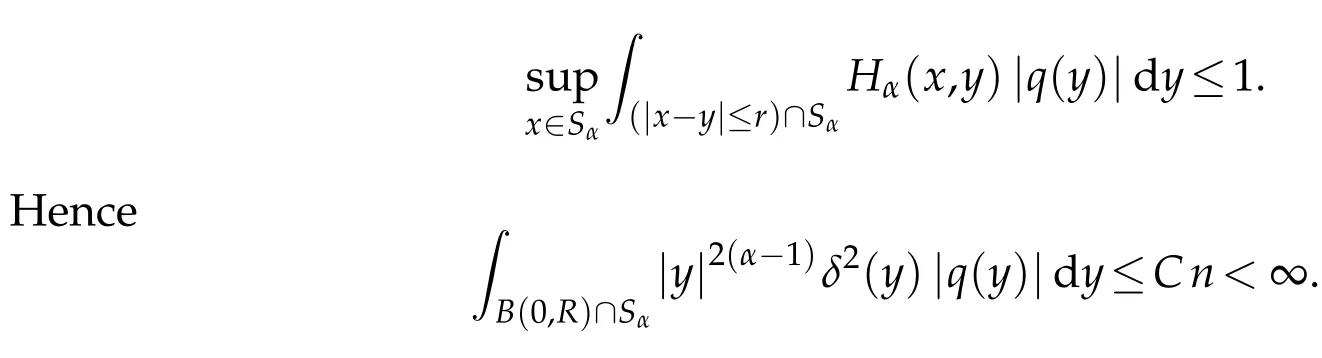
The p roof is com p lete.
Proposition3.3.Ifq∈J,then k q k<+∞.
Proof.Using Proposition 2.1,w e get
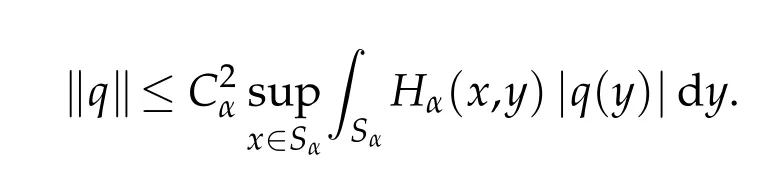
Let r>0 and M>0.Then,w e have

By(2.3)and Proposition 3.1,w e obtain

The resu lt follow s from(1.3),(1.4)and Proposition 3.2.
Proposition3.4.Let h beapositive superharmonic function in Sαand q in J.Then

Proof.Let h bea positive superharm onic function on Sα.By[11,Theorem 2.1],thereexists a sequence(fn)n∈Nof positivem easu rable function on Sαsuch that
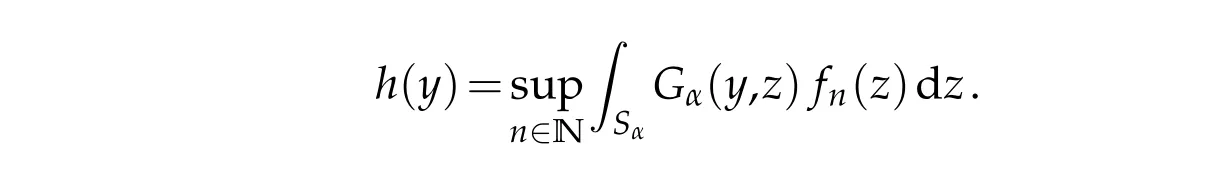
Hence,w e need on ly to verify(3.3)-(3.5)for h(y)=Gα(y,z)uniform ly on Sα.
1.Let r>0.Then by Theorem 1.1,w e have
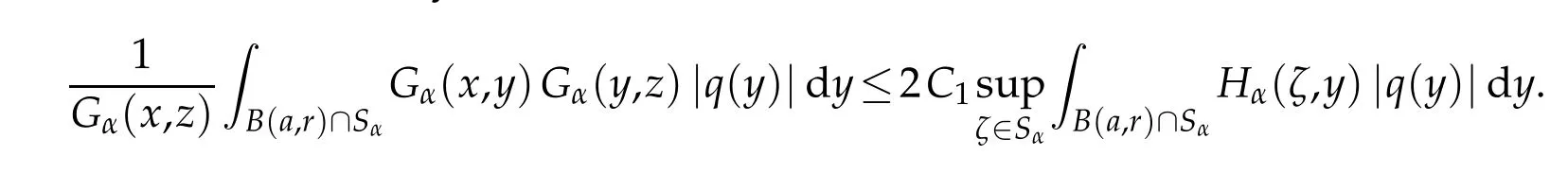
Letηand M>0.By using(2.6),w e get

We obtain(3.3)by using(1.3),(1.4)and Proposition 3.2.
On the other hand,

2.(3.5)follow s imm ed iately by using Theorem 1.1.
Corollary3.1.Letq bea Borelmeasurablefunction in J.Then,
Proof.By using(3.5)w ith h=1 and Proposition 3.3,w e obtain(3.7).Let x0∈Sα.By(2.6) and(3.7)w e get

Finally,(3.9)follow s from(3.8).
Proposition3.5.Letη,µ∈R such thatη<2<µandα∈]12,1[.Then thefunctionσdefined on Sαby

is in J.
Proof.Letη,µ∈R such thatη<2<µand r>0.Then w e have
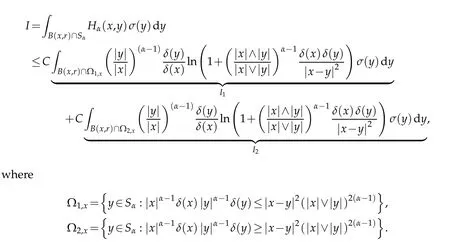
Let us recall that ifα∈]12,1[,then|x-y|(|x|∨|y|)α-1≤21-α|x-y|α.This im p lies by using Lemm a 2.1,that
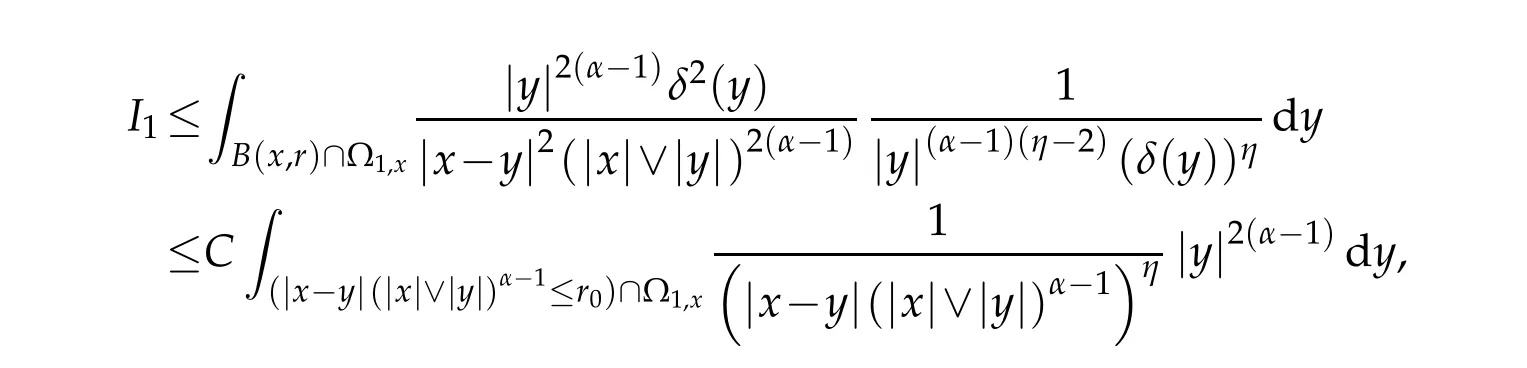

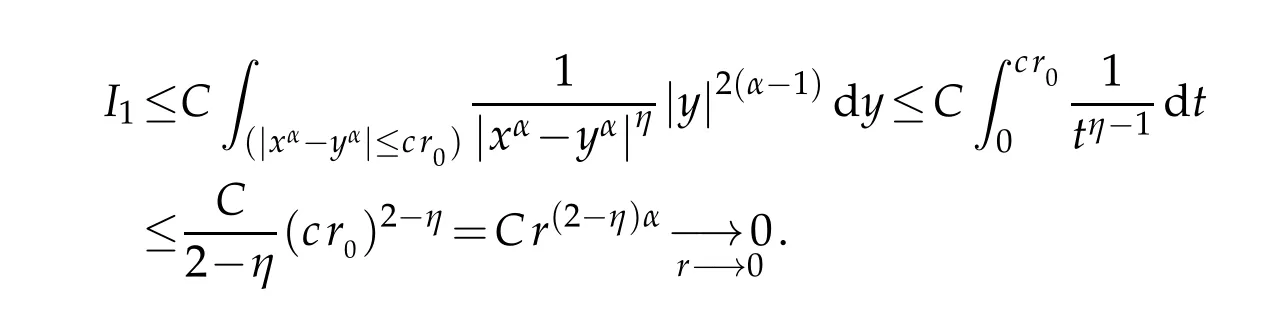
On the other hand,by Lemm a2.1 there exists C>1 such that for all y∈Ω2,xw e have
Since ln(1+t2)≤C tγ,∀t≥0,∀γ∈](0∨η),2[,then
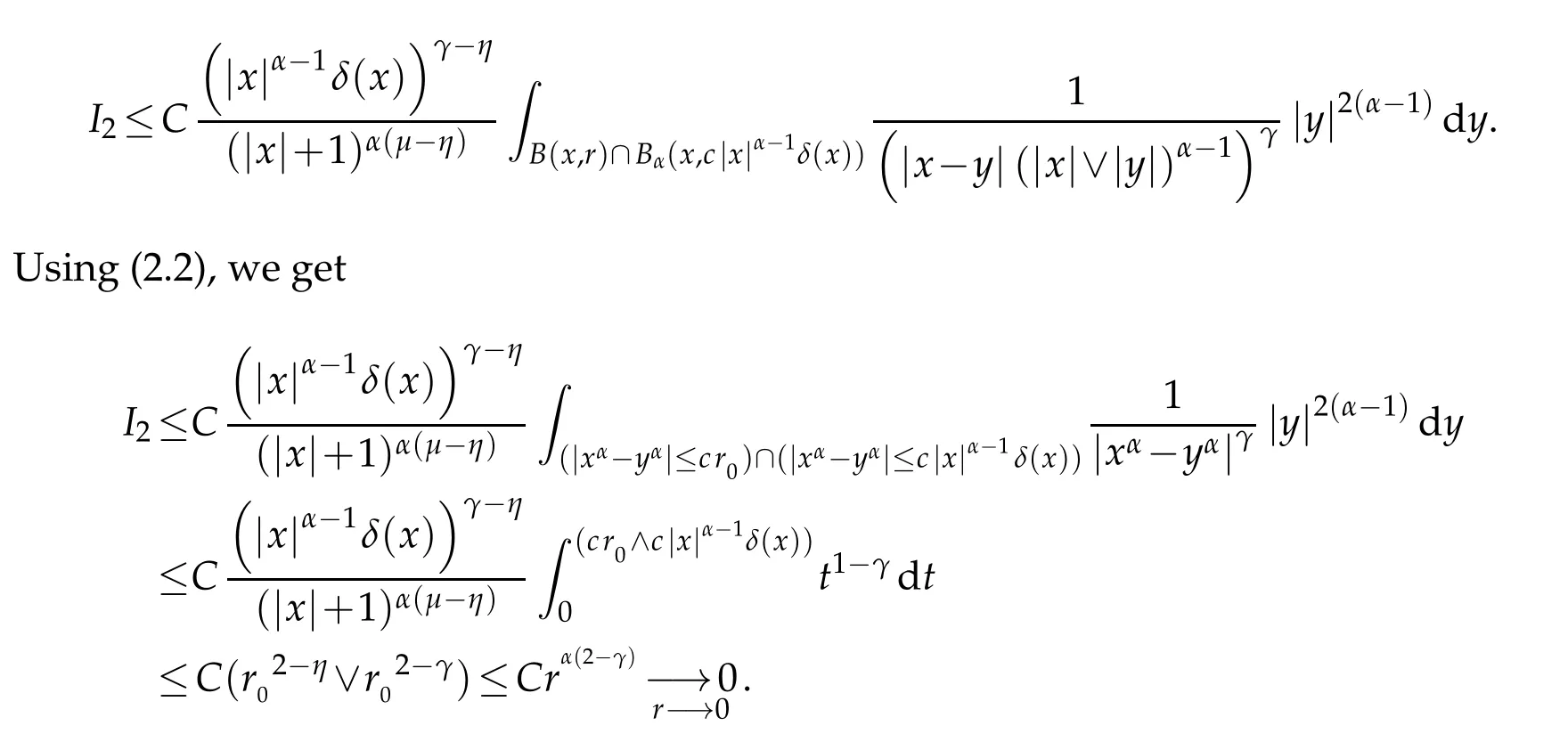
Now let M>0,
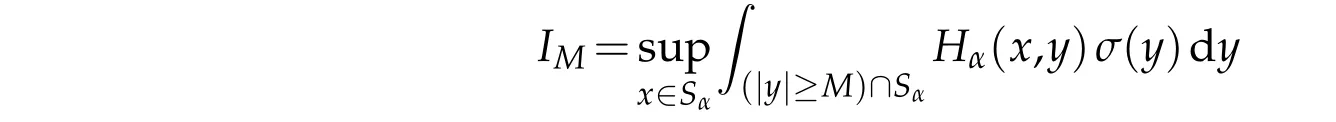
and show ing that limM-→+∞IM=0.Letε>0,then there exists r>0 such that
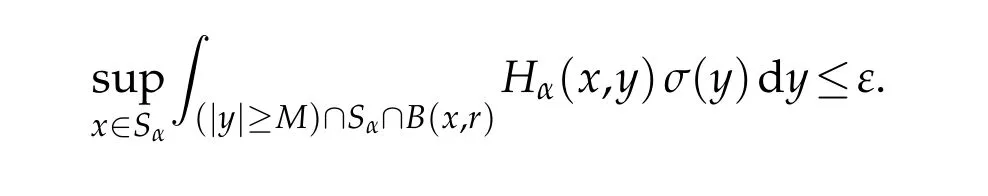
Then
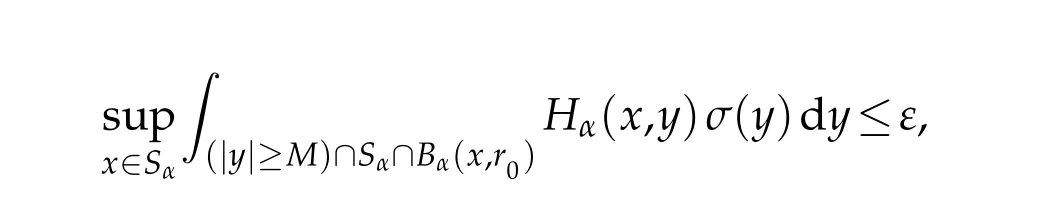
w here r0=21-αrα.
Fixing this r0>0 and letting M>1,w e get

Since the function z7-→zαis a conform alm apping,by using(2.2)w e obtain

The p roof is com p lete.
Lemma3.1.Let hα(x)=|x|αcos(αarg x),x∈Sα.Let M>0 and r>0.Then there exists a constant C>0,such that forall x,y∈Sαsatisfying|x-y|≥r and|y|≤M

4 Proof of Theorem 1.2
Let C(Sα)denotes the space of allbounded con tinuous functions in Sαendow ed w ith the uniform norm k k∞and let
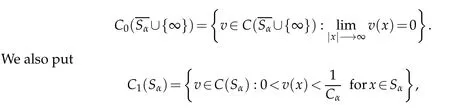
w here Cαis the constant defined in Proposition 2.1.For v∈C1(Sα),w e define

In the follow ing,for sim p licity,w ew rite q(y)=|V(y)|+ψ(y).
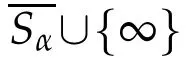
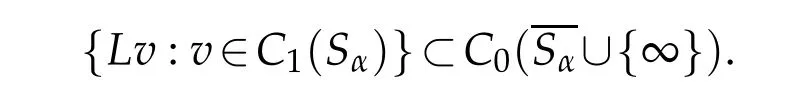
Proof.Let x0∈and r>0.Let M>|x0|+r,and x,It follow s from(H1) and v≤1/Cαthat
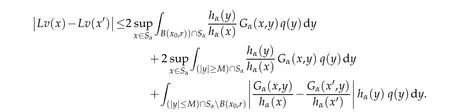
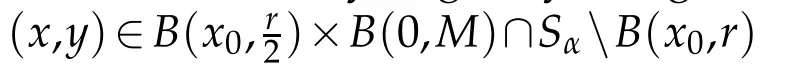


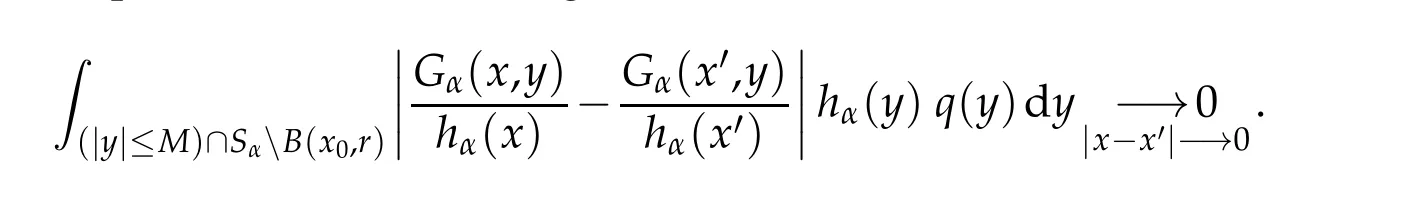
Hence Lv is continuous in Sαuniform ly for v∈C1(Sα).
We next consider x0=∞.Let M>0 and x∈Sαsuch that|x|≥M+1,then
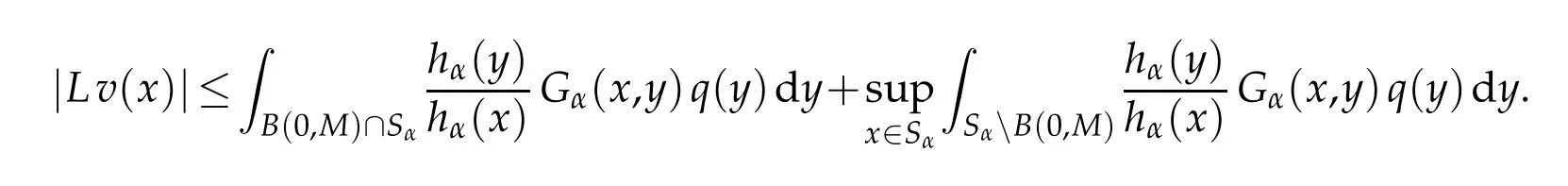
By(1.4),the second term of the righ t hand side is bounded byε,w henever M is su fficiently large.Note that from Proposition 3.1 and Lemm a 3.1,there exists C>0 such that
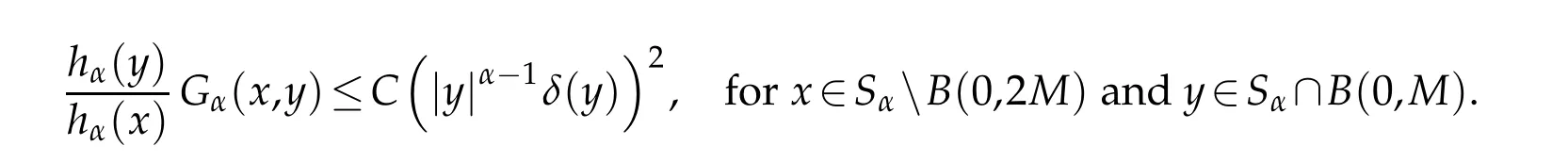
It follow s from Proposition 3.2 and Lebesgue’s convergence theorem that

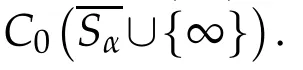

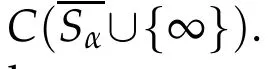
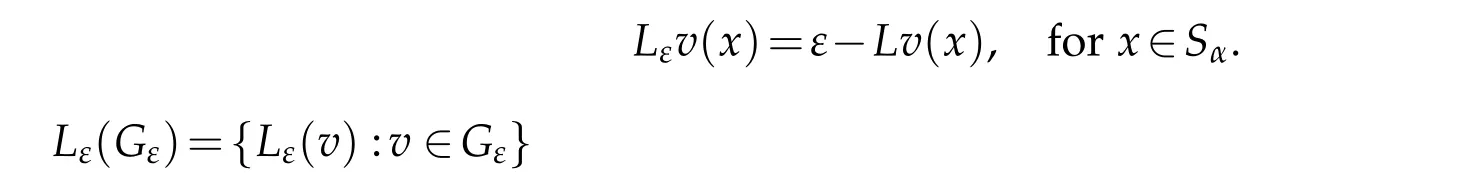
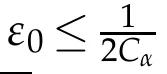
M oreover,Lε(Gε)isrelatively compact in C(Sα∪{∞}).
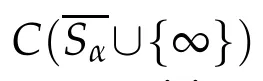
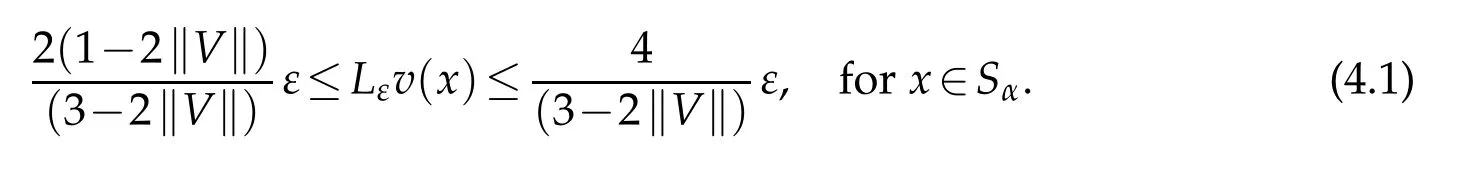
Let0<λ<1 and define

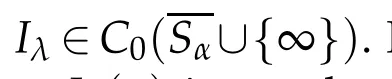
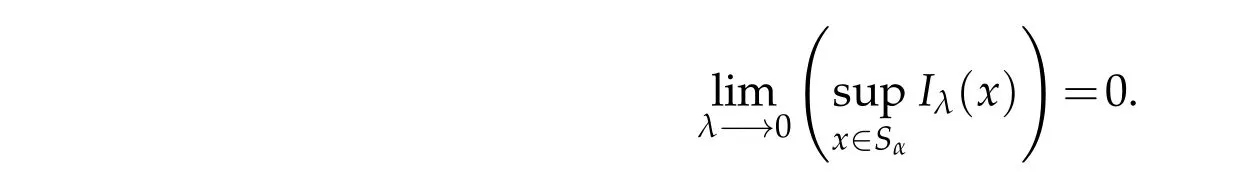
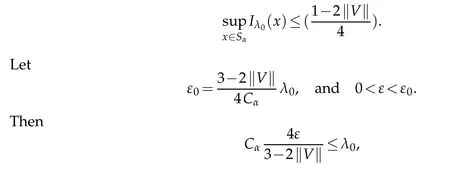
so it follow s from(H1)that for x∈Sα,w e have
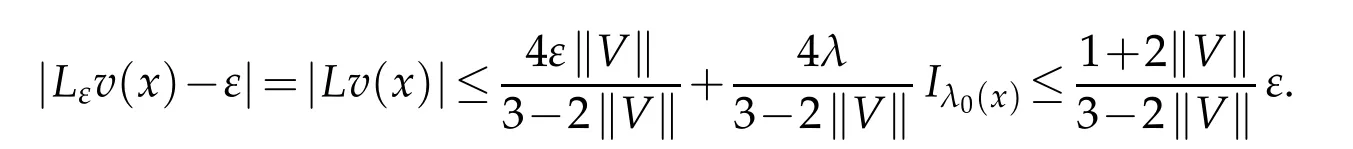
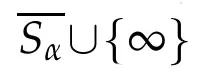
Lemma4.3.Let0<ε<ε0.Then Lεis continuouson Gε.
Proof.Let(vk)kbe a sequence in Gεw hich convergesuniform ly to v∈Gε.It follow s from (H1)-(H3)and Lebesgue’s theorem that

Since Lε(Gε)is a relatively com pact fam ily in C(Sα∪{∞}),the pointw ise convergence im p lies the uniform convergence.Therefore k Lεvk-Lεv k∞-→0 as k-→+∞.Thus Lεis continuouson Gε.
ProofofTheorem1.2.Let 0<ε≤ε0,w hereε0is the positive constant defined in Lemm a
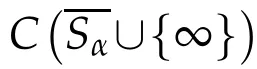

Let u(x)=v(x)hα(x).Then u>0 in Sα,and u=0 on∂Sαsince hαsatisfies these cond itions. A lso,w e have for x∈Sα,


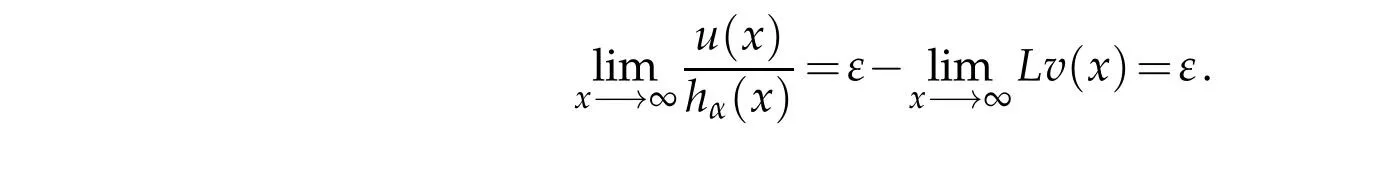
The p roof is com p lete.
Example4.1.Letν>0,α∈]12,1[andη<2<µ.Let h be a Borelm easu rable function on Sαsuch that

Then,there existsε0>0 such that for eachε∈(0,ε0],the p roblem
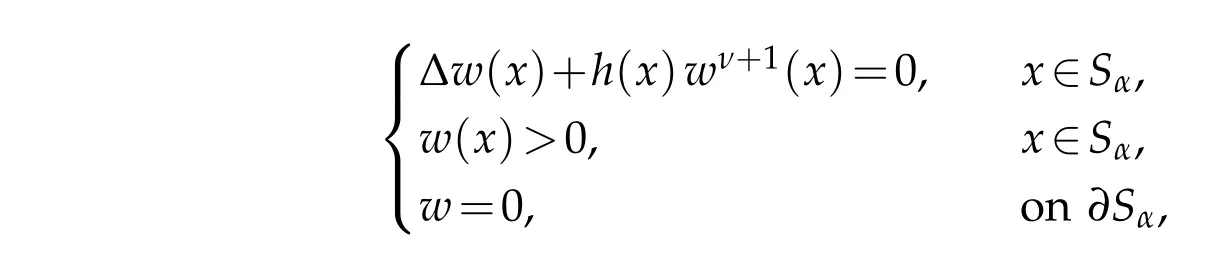
has a solution w continuouson Sαand satisfying
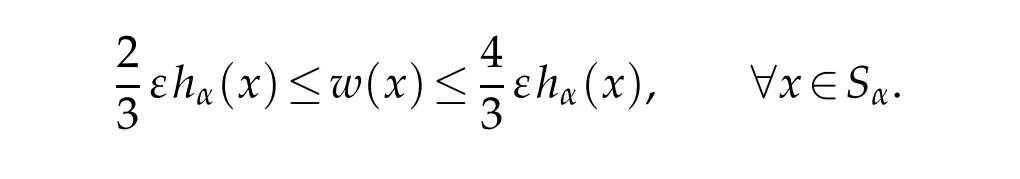
[1]Edelson A.L.,Entiere solu tions of singu lar ellip tic equations.J.M ath.Anal.Appl.139(1989), 523-532.
[2]Lair A.V.,Shaker A.W.,Entiere solutions of a singu lar sem ilinear ellip tic p roblem.J.M ath. Anal.Appl.200(1996),498-505.
[3]Lair A.V.,Shaker A.W.,Classicaland w eak solu tions of a singu lar sem i-linear ellip tic p roblem.J.M ath Anal.Appl.211(1997),371-385.
[4]Lazer A.C.,M ackenna P.J.,On a singu lar nonlinear ellip tic boundary-value p roblem.Proc. Amer.M ath.Soc.111(1991),721-730.
[5]U fektepe U.,Zhao Z.,Positive solutions of nonlinear ellip tic equations in the euclidean p lane.Proc.Amer.M ath.Soc.126(1998),3681-3692.
[6]Zhao Z.,On the existence of positive solu tions of non linear ellip tic equations-a p robabilistic potential theory app roach.Duke.M ath.J.69(1993),247-258.
[7]Zhao Z.,Positive solu tions of non linear second order ord inary d ifferential equations.Proc. Amer.M ath.Soc.121(2)(1994),465-469.
[8]Bachar I.,M aagliH.,M aatoug L.,Positive solutions of nonlinear ellip tic equations in a half space in R2.Electronic.J.D iff.Eqns.41(2002),1-24.
[9]H irata K.,Sharp Estim ates for the Green function,3G inequalities,and non linear Schrod inger p roblem s in uniform cones.J.D’analyseM ath´ematique,99(2006).
[10]Boubaker M.A.Ben,Selm iM.,Estim ation of Green’s function on piecew ise Dini-sm ooth Bounded Jordan dom ains.Collo.M ath.133(1)(2013),1-22.
[11]Port S.,Stone C.,Brow nian M otion and Classical Potential Theory.Probab.M ath.Staist, Academ ic Press,New York,1978.

10.4208/jpde.v27.n3.2 Sep tem ber 2014
∗Correspond ing au thor.Emailaddress:MohamedAmine.BenBoubaker@ipein.rnu.tn(M.A.Ben Boubaker)
AMSSubjectClassifications:31A10,31A25,31A35,34B15,34B27,31C45,35J65
ChineseLibraryClassifications:O175.5,O175.8
猜你喜欢
杂志排行
Journal of Partial Differential Equations的其它文章
- On Existence of Local Solu tions of a M ovingBoundary Prob lem M odelling Chem otaxis in 1-D
- Strong Solu tions for Nonhom ogeneousIncom p ressib le Viscous Heat-Conductive Fluidsw ith Non-New tonian Poten tial
- Liquid Crystal Flow sw ith Regu larity in One D irection
- WaveletCollocation M ethods for Viscosity Solu tions to Sw ing Op tions in Natu ral Gas Storage
- Quenching Tim e fora Sem ilinearHeatEquation w ith a Non linear Neum ann Boundary Cond ition
- Jacobi Elliptic Numerical Solutions for the Time Fractional Variant Boussinesq Equations
