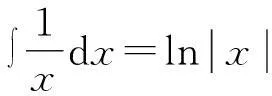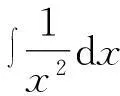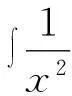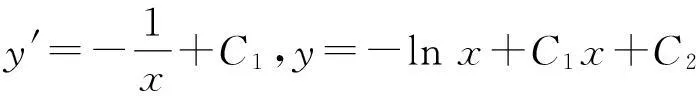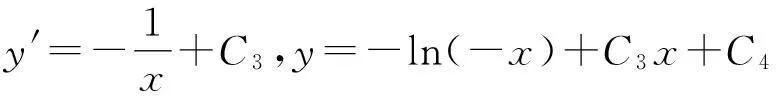大学数学教材内容存在的问题及其解决办法

梁 莉　李胜军

(海南大学信息科学技术学院， 海口 570228)



大学数学教材内容存在的问题及其解决办法

梁 莉李胜军

(海南大学信息科学技术学院， 海口 570228)

摘要：针对数学教材中基本初等函数结构、不定积分与常微分方程通解不完善的问题，利用积分上限函数对数学分析中的基本初等函数作出定义，并根据不定积分和常微分方程通解的定义进一步完善通解的解法。

关键词：基本初等函数； 不定积分； 微分方程； 通解

《数学分析》和《高等数学》是重要的大学数学基础理论课程，有多种相关教材。在10多年的教学当中我们接触到20余种大学数学教材，发现这些教材中90%以上都存在与数学基本思维方式相悖的内容，现予以指出。

第一个问题存在于教材最前面的内容中。其中提到初等函数是由常函数、幂函数、指数函数、对数函数、三角函数和反三角函数这些基本初等函数经过有限次的加、减、乘、除和复合而构成，除了常函数、三角函数、反三角函数和一些特殊的幂函数在中学的课本中有定义之外，其他基本初等函数均未给出数学定义； 在这种情况下即讨论幂函数、指数函数、对数函数的基本特性、运算法则和函数图形，进而得出了其导数和积分的表达式。这显然与数学理论中定义的准确性、表达的严密性、推理的逻辑性等思想相悖。此处存在的问题是：在讨论性质之前，首先未给出重要函数的定义。

第二个问题是不定积分的定义不够准确。不定积分指的是被积函数所有原函数的一般表达式，但基本所有的教材都存在一个同样的错误，所求的不定积分甚至不定积分公式都仅给出了被积函数的一部分原函数的表达式，作为不定积分的推广形式——常微分方程也存在同样的错误。

以上教材中存在的问题显然与准确的定义、简洁清楚的数学语言表达、严密的逻辑推理等一些数学思维相违背，这也是数学课程需要教给学生掌握的基本思想和处理方法。在此，详细讨论其中存在的问题，并提出相应的解决办法。

1几个基本初等函数的定义及性质

下面将利用数学分析中的积分上限函数作为工具，给出教材中没有严格定义的基本初等函数的定义，并利用这些定义来讨论这些基本初等函数的性质和运算法则[1]。

1.1对数函数的定义及基本性质

下面首先由如下积分上限函数给出对数函数的定义，进而由定义给出其基本性质。

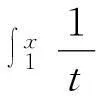
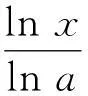
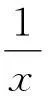
(4) ∀x,y>0，有等式 lnxy=lnx+lny成立，从而也有 logaxy=logax+logay。

证明性质 (1)、 (2) 和 (3) 可由定积分和导数的定义及基本性质直接推出。

证明性质(4)，设任意固定x0>0，设函数 f(y)=lnx0y，g(y)=lnx0+lny，首先证明f(y)≡g(y)。由于函数f(y)，g(y) 在(0,+∞)内是连续可导的, 并且有

f(1)=lnx0， g(1)=lnx0+ln 1=lnx0，

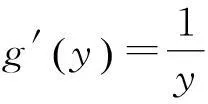
即f′(y)≡g′(y)。 由Lagrange中值定理的推论，有f(y)≡g(y)，再利用x0 的任意性，即有 lnxy=lnx+lny。 证毕。

1.2指数函数的定义和基本性质

根据上述内容中对数函数的性质(2)和(3)，可知lnx和 logax 在(0,+∞)内都是严格单调的函数，因而它们的反函数也都存在，利用其反函数即可给出下面的定义。

定义2称自然指数函数y=lnx的反函数为自然指数函数；一般对数函数 logax 的反函数称为以 a 为底的一般指数函数，分别用 ex 和 ax 表示。

关于指数函数可由其定义、对数函数的基本性质以及反函数的求导法则直接得出以下简单性质。

性质2(1) 当x>0 时ax>1，当 x<0 时 ax<1 并且 a0=1。

(2)一般指数函数ax 的导函数为 ax lna，因此当a>1 时，ax 在 (-∞,+∞) 内是严格单调递增的，当 0

(3) 对任意的x,y>0，有等式ax+y=ax·ay 成立。

1.3幂函数的定义及性质

在此我们将利用指数函数和自然对数函数的复合运算来给出幂函数的定义。

定义3对给定常数α∈R，称自然指数函数eu和常数α与自然对数函数lnx 的乘积函数 u=αlnx 的复合函数eα ln x为幂函数，其中 α 称为该函数的幂指数，可表示为 xα=eα ln x。

由定义可得到如下一些基本性质。

性质3(1) 对任意的 x>0，xα>0 且当α=0时x0=1。

(2) 幂函数 xα的导数为αxα-1，对任意的 x>0，当 α>0 时函数 xα单调递增，当α<0 时函数xα单调递减。

(3) 对任意的 x>0 有等式 xα+β=xα·xβ成立。

(4) 对 a>0且 a≠1，对任意的 x>0 和任意的 α∈R有logaxα=αlogax。

证明由幂函数的定义直接得到性质(1)和(3)。 由对数函数的导数和复合函数的求导法则可得性质(2)。 因此我们只对性质(4)加以证明，要证性质(4)成立也只需证lnxα=αlnx 成立即可。

任取 α∈R和对任意的 x>0，令函数 f(x)=lnxα和g(x)=αlnx，由于 f(x)和 g(x)在区间(0,+∞)内是连续可导的函数，并且有

f(1)=0，g(1)=0，

因此在(0,+∞)内有 f′(x)≡g′(x)。 同性质1中(4)的证明一样，利用Lagrange中值定理的推论即可得出函数 f(x)≡g(x) 。 证毕。

另外利用方程、函数的极限和导数作为工具，还有关于基本初等函数的其他结构性定义[2]，这里就不一一赘述。

2初等函数在教材中应合理安排

在大学数学分析和高等数学教材中，一部分基本初等函数如幂函数、指数函数和对数函数在没有给出定义的基础上就直观地给出了它们的基本性质、运算法则和图象等要素，学生只能被动地接受这些理论。 本文基于上述基本初等函数的定义及相关性质所需要的知识内容，建议对基本初等函数在教材中所处的位置安排作以下调整。

在大学数学分析和高等数学讲授的内容中可以不用先讲基本初等函数。在讲授了一般函数的极限导数、积分的内容之后，再由积分的运算性质和积分上限函数来定义自然对数 lnx和以a为底的对数函数 logax， 利用其反函数来得到自然指数函数 ex 和一般的指数函数 ax 的定义， 同上述定义一样采用函数复合的方法来给出幂函数 xα 的定义，再来讨论这些基本初等函数的基本性质、函数图形、运算法则、导数和积分公式等，从而使得基本初等函数在教材中具有一个较为系统合理化的安排。

3常微分方程部分的错误应予纠正

这里C1 和 C2 是两个不同的任意常数。 由于这个不定积分公式中存在的缺陷，从而导致具有间断点的有理函数的不定积分以及系数函数具有间断点的常微分方程的通解中也存在同样的错误。

针对上述错误给出如下解决办法：利用常微分方程中系数函数的不可去间断点，将实数集分成不同的区间段，在每一个区间段分别求出常微分方程的通解。现给出一些简单实例。

所以原方程的通解为

而不能直接写成通常教材中的表达式

参考文献

[1]陈纪修，於崇华，金路. 数学分析[M]. 北京:高等教育出版社， 1999：15-21.

[2]胡永忠，曾平华. 几个基本初等函数的公理化定义[J]. 广东教育学院学报， 2001，21(2): 29-31.

[3]丁同仁，李承治. 常微分方程教程[M]. 北京:高等教育出版社，2004：4-8.

[4]同济大学数学教研室. 高等数学[M]. 北京:高等教育出版社，1996：226-228

[5]盛祥耀. 高等数学[M]. 北京:高等教育出版社，1992：180-181

AnalysisoftheProblemsinMathematicsTextbooksandTheirSolutions

LIANG LiLI Shengjun

(SchoolofInformationScienceandTechnology,HainanUniversity,Haikou, 570228,China)

Abstract:This paper makes scientific definitions about the basic elementary functions using integral upper limit function, and improves their general solution methods in accordance with the definition of indefinite integral and ordinary differential equations.

Key words:basic elementary functions; indefinite integral; differential equations; general solution

文献标识码：A

文章编号：1673-1980(2015)02-0126-03

中图分类号：O241：G642

作者简介：梁莉( 1978 — )，女， 四川内江人，讲师，研究方向为常微分方程研究。

基金项目：海南省自然科学基金项目(113003)； 海南大学2013年度校级教育教学研究项目(HDJY1331)

收稿日期：2014-11-10