线性代数课堂趣味渗透法教学实践

郭 竹 梅

(安徽科技学院数理学院， 安徽 凤阳 233100)



线性代数课堂趣味渗透法教学实践

郭 竹 梅

(安徽科技学院数理学院， 安徽 凤阳 233100)

摘要：在线性代数课堂教学中引入趣味渗透教学法，以提升教学效率。针对线性代数课程抽象性与逻辑性较强的特点，挖掘其定义、性质、公式、定理中美的特性,或通过一题多解的讲解使知识体系条理化，增强趣味性，激发学生的学习兴趣 。

关键词：线性代数； 趣味渗透教学； 学习兴趣

线性代数是高等院校设置的一门主要基础理论课程，具有较强的抽象性和逻辑性。目前大多数院校线性代数的学时设置较少，且很多线性代数教材偏重于理论证明而疏忽了模型的实践应用。因此，笔者尝试在课堂教学中引入趣味渗透教学方法，改变沉闷的传统课堂教学方式，调动学生的学习积极性，提高课堂教学效率。

所谓“趣味渗透教学”，就是指教师通过各种有效的方式、方法，充分调动学生的积极性，从而圆满完成教学任务的课堂教学模式[7]。下面介绍课堂教学中的实践经验。

1通过数学审美教学进行趣味渗透

刚开始进行线性代数学习时，学生往往感到各种概念、定理、性质太过抽象，各种知识不易熟练掌握，仅凭死记硬背效果不佳。为了改变此现象，我们通过挖掘线性代数课程在定义、性质、公式、定理中美的特性，帮助大家学习线性代数。比如，在讲解矩阵时，列出以下运算公式：

(1) (A-1)T=(AT)-1

(A-1)*=(A*)-1

(A*)T=(AT)*

(2) (AB)T=BTAT

(AB)-1=B-1A-1

(AB)*=B*A*

(3) (An)T=(AT)n

(An)-1=(A-1)n

(An)*=(A*)n

这些相似的公式对比罗列起来，结构相近，变化中又有规律可循，具有和谐的美感。通过对比这些公式，使学生感知到其简洁美和统一美，相关知识点也容易记入脑海。

2通过一题多解进行趣味渗透

线性代数课程中知识点较多，前后相关性很强，如果不能融会贯通就会感到前后知识点杂乱无章，更易导致学习积极性受挫而丧失兴趣。这时我们可以采用一题多解的形式贯穿始终，使教学更加条理化，知识要点集中化，解题方式系统化。以下面的习题为例，我们可以集中列出4种证明方法：

例1若向量组α,β,γ线性无关，则向量组α+β,β+γ,γ+α也线性无关[8]。

证法一[8]：设有一组数x1,x2,x3，使

x1(α+β)+x2(β+γ)+x3(γ+α)=0

成立，整理得

(x1+x3)α+(x1+x2)β+(x2+x3)γ=0

因α,β,γ线性无关，故有

由于此方程组的系数行列式不为零，故该方程组只有零解x1=x2=x3=0，则向量组α+β,β+γ,γ+α线性无关。

证法二：易知

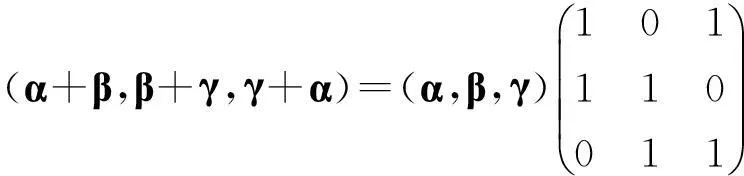
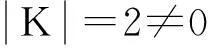
证法三 ：同证法2，得B=AK，设Bx=0，则AKx=0，又向量组α,β,γ线性无关，故Kx=0，因为K可逆，所以x=0，则向量组α+β,β+γ,γ+α线性无关。

3通过教学语言艺术进行趣味渗透

在课堂教学中，以比喻的方式使内容更加通俗易懂，学生学起来更加轻松。例如，在讲解逆矩阵的性质(AB)-1=B-1A-1时，可把A，B分别比喻为“穿袜子”，“穿鞋”，则AB为“先穿袜子后穿鞋”，其逆变换自然是“先脱鞋后脱袜子”，在讲解性质(An)-1=(A-1)n时，把A比拟为“穿袜子”，则An为“穿了n双袜子”，n双袜子一次性脱掉和一次脱一双袜子共脱n次效果显然是一样的，从而可形象地解释(An)-1=(A-1)n。

4通过理论应用进行趣味渗透

在课堂教学中，我们可以通过线性代数的理论简化中学中复杂方程的解法，使同学耳目一新，利用学生对这一现象的新鲜感来提高学习的兴趣。比如可用向量组的线性相关性解以下方程：

例2求方程的实数解：

解：令

易知

-7(1,2,1)+4(2,3,4)=(1,-2,9)

所以有

-7u2+4v2=w2

又u+v=w，得

-7u2+4v2=(u+v)2

化简得

(4u+3v)(2u-v)=0

所以有v=2u，即

此外，线性代数在现实中运用广泛，在教学中要使学生认识到线性代数并非“学而无用”。例如，讲解矩阵时，可列举几个城市的路线应用问题；讲解矩阵乘法时，可列举工厂的利润应用问题；讲解逆矩阵时，可列举密码学应用问题等。课堂之外，可以组织数学趣味知识大赛，让学生自已观察并发现数学的趣味性，使他们从内心深处喜爱数学。

课堂趣味教学法的实践取得了良好效果，学生对线性代数课的学习兴趣极大提高。通过成绩统计对比，接受实践趣味教学法授课的学生成绩明显高于其他学生。

5结语

综上所述,将趣味渗透教学引入课堂是一种有意义的教学实践，在一定程度上激发了学生的学习兴趣，提高了课堂教学效率。趣味渗透教学法方式多种多样，并非固定单一，需要教师在运用当中逐渐摸索，以找到适合课堂特点的教学方法。只要能够激发学生学习兴趣的手段都可以运用，但是老师在运用趣味渗透法来教学时，所引用的比喻或故事应恰当，应围绕所要传授的知识点，以避免偏离主题。

参考文献

[1]孙杰. 应用型人才培养中的线性代数课程教学模式的研究与实践[J]. 赤峰学院学报(自然科学版)，2009， 25 (12)：21-22.

[2]岳晓鹏，孟晓然. 在线性代数教学改革中融入数学建模思想的研究[J]. 高师理科学刊，2011，31(4)：77-79.

[3]李小平. 关于《线性代数》教学改革的一些思考[J]. 大学数学，2011，27(3)：22-25.

[4]陈平炎. 线性代数课程教学改革的探索与实践[J]. 高等理科教育，2012(5)：120-123.

[5]欧阳异能，王继红. 线性代数课程教学改革的思考与探索[J]. 中国电力教育，2014(14)：152-153.

[6]高彦伟，白岩，陈殿友. 非数学专业线性代数课程学习评价模式改革研究[J].长春师范学院学报(自然科学版)，2008，27(4)：114-116.

[7]荀书丰. 浅谈实施数学趣味教学的途径[J]. 丹东师专学报，2003，25(3)：109-110.

[8]吴赣昌. 线性代数：经管类[M].第5版. 北京:中国人民大学出版社，2011:99.

The Practice of Interesting Teaching Infiltration in Linear Algebra

GUOZhumei

(College of Mathematics and Physics, Anhui Science and Technology University, Fengyang Anhui 233100, China)

Abstract:In view of much abstractness and logic in linear algebra, this paper introduces interesting teaching infiltration for developing students’ learning interest. Based on the beauty in definition, quality, formula and theorem of linear algebra, the interesting teaching infiltration could increase the interest of the class as well as make the knowledge system organized combined with multi-answer of the same problem.

Key words:Linear Algebra; interesting teaching infiltration; learning interest

文献标识码：A

文章编号：1673-1980(2015)02-0124-02

中图分类号：O29:G642.0

作者简介：郭竹梅(1980 — )，女，安徽淮北人，讲师，硕士，研究方向为微分方程及其应用。

基金项目：安徽省振兴计划教研项目(2014ZDJY098)

收稿日期：2014-11-27