拉杆松弛导致预紧失谐组合转子性能退化研究

第一作者苏永雷男，硕士生，1989年生

通信作者王艾伦男，教授，博士生导师，1959年12月生

拉杆松弛导致预紧失谐组合转子性能退化研究

苏永雷1,2，王艾伦1,曾海楠3

(1.中南大学高性能复杂制造国家重点实验室，长沙410083； 2.重庆长安汽车股份有限公司(研究总院)，重庆401120;3.天津大学机械工程学院，天津300072)

摘要：由结构损伤导致性能退化角度出发，分析拉杆松弛引起的预紧失谐组合转子性能退化特性。利用跨尺度计算方法获得轮盘界面接触刚度并对接触界面等效处理，提出考虑粗糙界面及预紧的组合转子动力学建模方法。在此基础上进行组合转子动力学分析，获得组合转子固有频率随时间变化规律；建立以组合转子频率相对降低量表征其性能退化量的定量评估方法，对退化数据进行处理并描述组合转子退化轨迹，实现拉杆松弛引起的组合转子性能退化定量评估；对初始预紧失谐程度相同的组合转子进行不平衡响应分析，获得预紧失谐组合转子退化特征。结果表明，组合转子性能退化量参数服从指数函数分布，负失谐对组合转子不平衡响应影响较大。

关键词：拉杆松弛；组合转子；退化量；失谐；固有频率

基金项目：国家973计划资助项目(2013CB035706)

收稿日期：2014-03-25修改稿收到日期：2014-06-24

中图分类号:TH113.1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.20.005

Abstract:A combined rotor is the key part of an engine, and it is important to reveal its degradation mechanism and assess the performance degradation degree for making maintenance during operation. Performance degradation characteristics of the combined rotor were discussed, from the perspective of performance degradation caused by structural damage. The dynamic features of the combined rotor were analyzed, considering the rod relaxation and interface contact effect and the changing of natural frequency along with the time was observed. Then, by defining the degradation degree of combined rotor, the degradation path was described through processing the degradation data and the degradation assessment was completed as well. At the end, unbalance responses of combined rotors with the same mistuned degree of preload were investigated and the degradation characteristics of combined rotors were obtained. The results show that: degradation parameters of combined rotors have exponential distribution, and the negative mistuning has great effect on the unbalance response amplitude of combined rotors.

Performance degradation of mistuned combined rotor considering rod relaxation

SUYong-lei1,2,WANGAi-lun1,ZENGHai-nan3(1. Key Laboratory of High performance and Complex Manufacturing, Changsha 410083, China;2. Chongqing chang’an automobile Co., Ltd., Chongqing 401120, China;3. School of Mechanical Engineering, Tianjin University, Tianjin 300072, China)

Key words:rod relaxation; combined rotor; degradation degree; mistuning; natural frequency

运行中由于蠕变、裂纹、磨损等原因设备性能会逐步退化，不但降低其可靠性更增加其发生故障的可能性。作为长期严酷工况运行造成组合转子性能退化的有力佐证，GE公司10余台9FA机组连续发生严重振动超标，且故障大多出现于机组运行10000小时以上，主要原因为组合转子间预紧力在长期运行中逐渐缺失导致预紧力不足，在轮盘间发生滑移，改变转子的应有刚度；该公司另一主打机组LM5000燃气轮机运行中也出现压气机随机组负荷增加、振动加剧现象[1]。而某台燃机中间轴及压气机24个连接螺栓因其中1个螺栓破坏导致转子振动过大，导致重大事故发生[2]。

工业实践中因制造误差、材料缺陷等因素使转子系统循环对称性遭受破坏导致系统失谐。转子最典型的失谐形式为叶盘系统失谐，主要反映为模态局部化及振动传递局部化。结构动力学中此两种局部化称为失谐周期结构振动局部化问题，且广受关注[3]。而对周向拉杆组合转子则存在另种形式失谐即各拉杆预紧不均匀导致的失谐。若一根拉杆预紧力与其它拉杆不同，则该拉杆在转子弯曲时的受力亦不同于其它拉杆，因而导致转子弯曲刚度改变，并产生各向异性。该失谐不同于叶盘的弱耦合结构失谐，而类似裂纹转子产生的刚度各向异性[4]。

燃气轮机长期服役于高温、高转速工况，对其进行性能退化特性研究、掌握性能退化程度及趋势对保障燃气轮机安全运行具有重要意义。Diakunchak[5]认为燃气轮机性能退化不仅与运行时间相关，亦受工作模式影响。Brook[6]认为燃气轮机大部分能量损失由压气机部分性能退化所致。Kurz等[7]通过对燃气轮机性能退化原因详细阐述，研究不同退化成因导致的燃气轮机系统性能参数变化。据燃气轮机性能退化特征，Brothertom等[8]提出用浴盆曲线近似描述燃气轮机性能退化规律。Li等[9]利用气路分析方法对退化数据进行拟合，获得燃气轮机性能退化曲线，并用于预测燃气轮机剩余寿命。Venturini等[10]基于蒙特卡洛法，提出可靠诊断与预测燃气轮机退化方法。

现有研究存三方面问题：①燃气轮机退化研究主要集中在不同退化成因对整机性能参数影响及诊断方式，而对其组合转子性能退化研究较少。组合转子作为燃气轮机能量转换的核心部件，其退化会对整机性能产生重大影响，但组合转子性能退化机理并不明确。②其退化量参数所选整机性能参数(功率、燃耗、压比)不适合作为组合转子退化量指标。③虽通过建立具有界面开闭效应的集中参数模型研究组合转子动力学问题，但对性能随时间退化研究尚少。为此，本文由结构损伤导致性能退化角度出发，研究拉杆松弛导致预紧失谐组合转子退化特征；定义退化量指标并建立组合转子退化量与时间的函数关系，揭示拉杆松弛引起的组合转子性能退化机理。

1组合转子计算模型

燃气轮机压气机段周向均布拉杆组合转子简化模型(简称组合转子)见图1，该转子由两端轴头、4个中间轮盘及8根拉杆组成。拉杆周向均布于直径Drod=80 mm圆上，将六级轮盘预紧组成整体，轮盘间具有多个接触界面，组合转子材料密度7800 kg/m3，轮盘、转轴弹性模量210 GPa。组合转子各物理参数见表1。

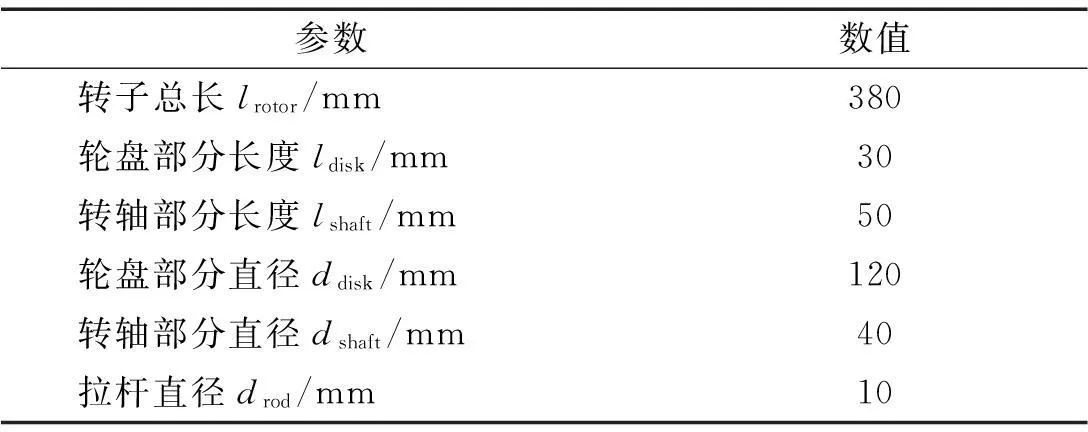
表1　组合转子物理参数

图1　组合转子结构示意图 Fig.1 Structure of compressor combined rotor

2组合转子界面刚度等效

接触界面的存在导致组合结构刚度发生变化，结构通过接触界面进行动力传递，不同界面状态直接影响结构的振动特性[11]。为准确进行组合转子动力学分析，在获得粗糙表面接触刚度基础上计算接触刚度与预紧力关系,进行接触刚度等效。

2.1界面刚度确定

直接在全尺寸模型中研究微米级粗糙度对界面刚度影响尺寸效应会较明显从而导致分析困难。本文采用具有相同界面粗糙度的微元体模型分析与宏观尺寸相结合的跨尺度计算方法获得轮盘间接触刚度，即①计算轮盘间(图 1)A接触界面面积S1并进行受力分析，获得预紧后界面压力P；②据文献[12]方法建立界面面积S2、粗糙度0.4 μm、压力P作用下微元体模型进行应力应变分析并提取该微元体模型法向接触刚度kn；③借鉴文献[13]，在获得微观有限元模型接触刚度基础上通过面积扩展，获得组合转子在预紧力F作用下界面法向接触刚K，见图2。面积扩展表达式为

F=PS1

(1)

(2)

图2　组合转子界面接触刚度与预紧力的关系图 Fig.2 Stiffness of interface versus pretension for combined rotor

2.2界面刚度等效

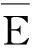
(3)

式中：h为虚拟材料层厚度。

3考虑界面的预紧失谐组合转子动力学建模

为进行组合转子谐调、失谐的退化研究，本文提出考虑粗糙界面和预紧情况的组合转子建模方法建立p根拉杆预紧(其中q根拉杆失谐)的失谐组合转子动力学模型，见图3。

图3　预紧失谐的组合转子建模 Fig.3 The model of preload mistuning combined rotor

据失谐的一般表达式，定义预紧失谐量为

ηi=(Fdi-Fh)/Fh

(4)

式中：Fh为谐调预紧力，Fih为组合转子第i根拉杆预紧力。则ηi>0为预紧正失谐，ηi<0为预紧负失谐，ηi=0为预紧谐调。

将第i根拉杆预紧力Fi等效为所有拉杆中最小预紧力F0与附加预紧力ΔFi两部分。即

Fi=F0+ΔFi

(5)

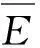
本文以8根拉杆预紧、1根拉杆发生失谐(P=8，q=1)为例，对失谐组合转子进行分析。

4拉杆螺栓松弛应力计算

联接件受蠕变、疲劳等多种作用，但在稳定载荷状态下最基本损伤机制为恒应变下应力松弛[14]。

松弛中，设ε0为联接件初始弹性应变且为常数。在绝对温度为T的环境中经时间t后弹性应变为εe，蠕变应变为εc，则有

ε0=εe+εc=σ/E+εc

(6)

式中：E为弹性模量。

对式(5)求导得

(7)

针对长期工作的拉杆松弛，用 Norton 模型表达蠕变应变速度与应力关系，即

(8)

式中：C1，C2，C3为材料常数。

拉杆初应力σ0符合

(9)

式中：σ0为拉杆初始应力；Δl为预紧量；lrod为总长；Arod为横截面积；F0为初始预紧力。

结合式(4)、式(7)～式(9)得拉杆松弛剩余应力为

σ={[(1+η)ε0E]1-C2-

(10)

拉杆预紧力F在t时刻符合

F=σArod

(11)

结合式(4)、(5)、(11)得预紧失谐产生的附加预紧力为

(12)

式中：σh为预紧谐调(η=0)时据式(10)所得应力值。

本文燃气轮机组合转子拉杆材料采用GH4169，利用蠕变实验数据确定Norton蠕变模型参数值[15]。其中C1=2.2E-9，C2=10.2，C3=50825。由材料特性[16]可得弹性模量E在不同温度T的数值。

参照工程中重型燃气轮机拉杆预紧情况，将初始预紧量定为拉杆总长的千分之一，即ε0=1/1000。据式(9)所得失谐拉杆在873 K温度下应力松弛曲线见图4，据式(11)所得预紧失谐量随时间变化见图5。由两图看出，材料为GH4169的拉杆在同一温度环境下失谐量随时间增加逐步减小，即各拉杆预紧力随时间增加趋于谐调；初始失谐量η*为10%(5%)的拉杆较初始失谐为-10%(-5%)的拉杆失谐量随时间增加更接近0值，即初始失谐量相当情况下随时间增加初始正失谐拉杆预紧力失谐程度较负失谐小。

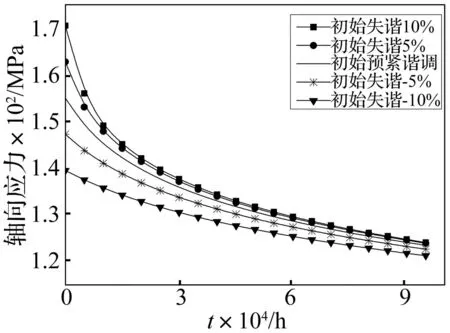
图4　失谐拉杆在873K温度下的应力松弛曲线 Fig.4 Stress relaxation curve of mistuning rod

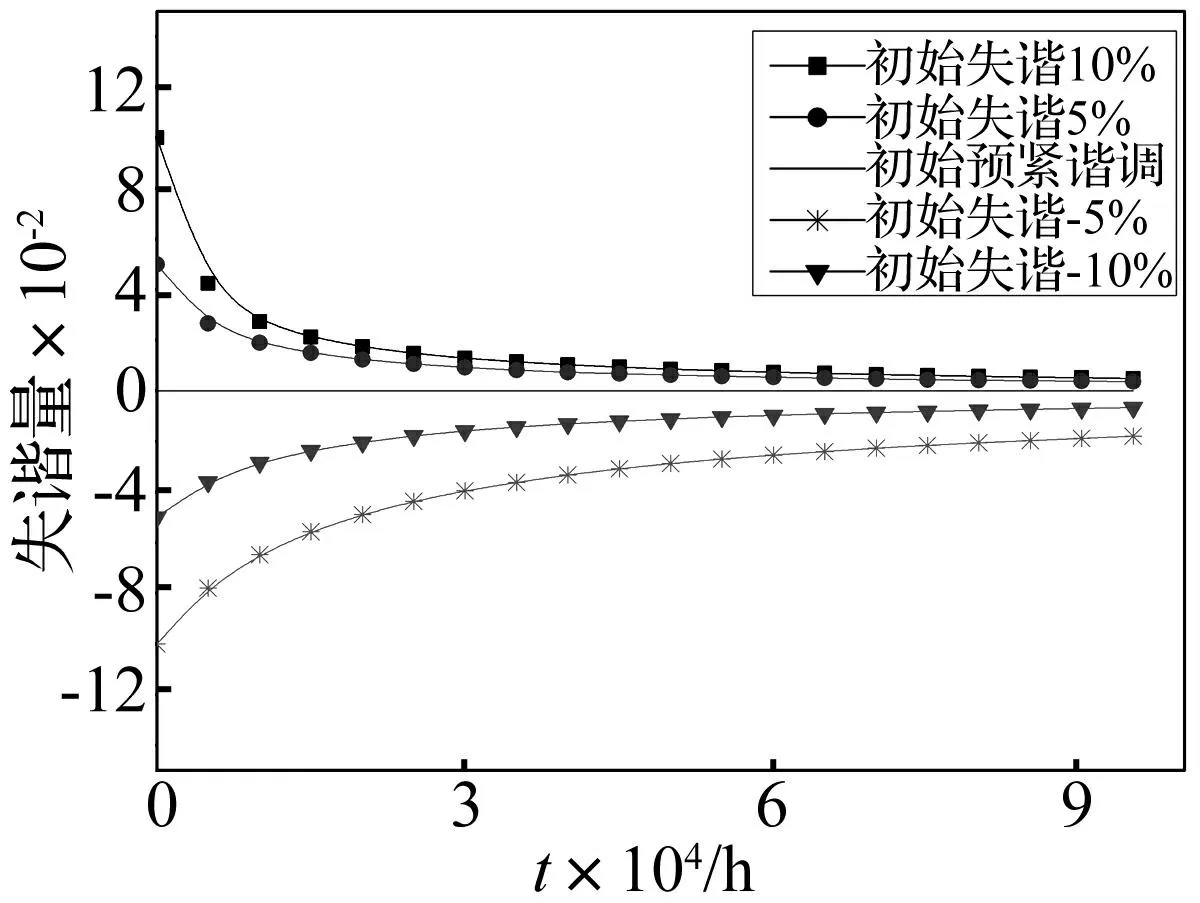
图5　失谐拉杆在873K温度下失谐量随时间的变化 Fig.5 Mistuning degree change with relaxation time at 873K

5组合转子固有特性分析

拉杆初始预紧不均产生的广义附加力矩影响转子刚度。为进一步研究拉杆松弛引起预紧失谐组合转子退化特征，对初始预紧失谐的组合转子在简单弹性支承下进行动力学分析。拉杆谐调预紧值由拉杆伸长量(拉杆长度的1/1000)确定。本文只分析组合转子弯振特性，不考虑界面切向刚度，虚拟材料层泊松比为0，厚度0.5 mm；转子工作温度873 K，转速3000 r/min。进行动力学分析时将拉杆螺母与轮盘间及虚拟材料层两端与轮盘接触界面粘合。

在同一时间段内组合转子受预紧降低、预紧失谐两因素耦合作用；通过调节虚拟材料层弹性模量表达组合转子预紧程度，调节拉杆附加预紧力表达预紧失谐量变化。以初始预紧失谐量-10%、0、10% 为例，在温度为873 K、转速3000 r/min 条件下对8根拉杆、6级轮盘组合转子进行含预应力的模态分析。附加预紧力据式(12)求得，计算所得组合转子固有频率见表2。由表2看出，预紧失谐对组合转子固有频率影响不大，且随松弛时间延长而减弱。此因失谐量为10%时预紧失谐绝对量F占拉杆总预紧力的1/80，对界面刚度影响较小；另外，随时间延长预紧失谐量逐步降低，失谐对组合转子固有频率影响降低。组合转子前三阶固有频率相对降低量在不同时间分布值相近，且频率相对降低量随时间呈递增趋势。

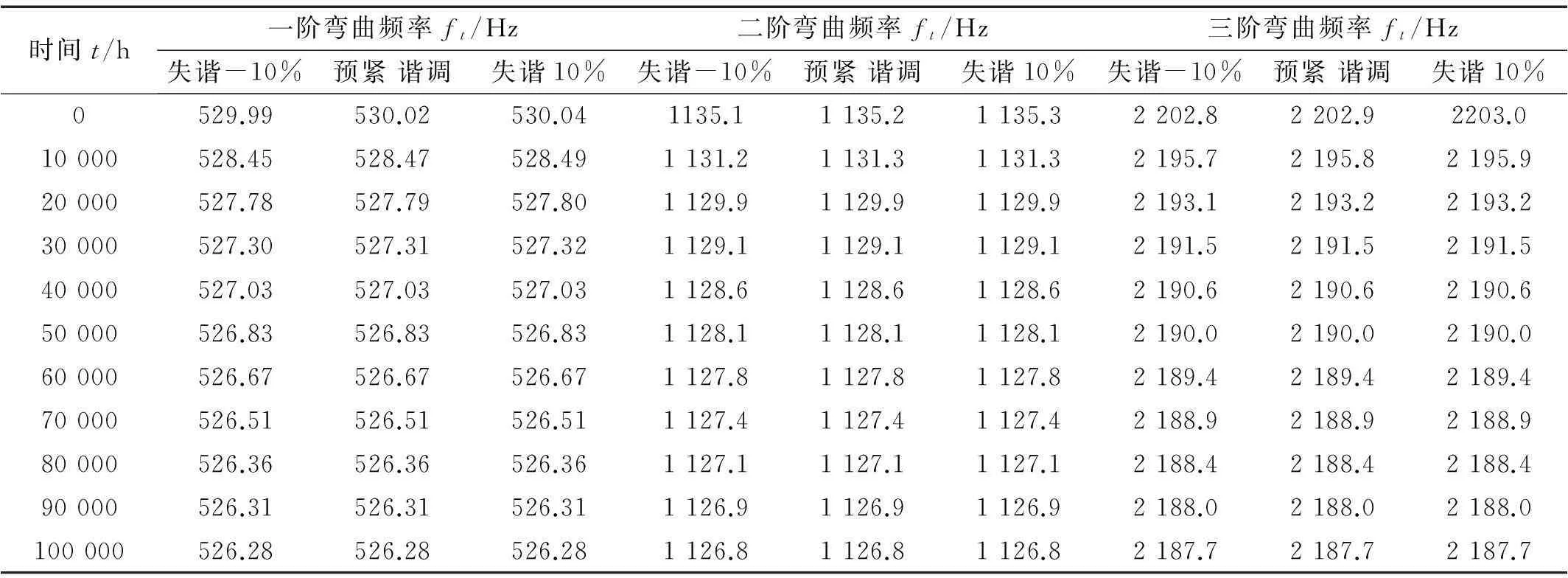
表2　组合转子固有频率随时间变化关系

6松弛引起失谐组合转子性能退化评估

为判断设备退化情况，本文选组合转子频率相对降低量作为拉杆松弛引起的组合转子性能退化量参数，退化量D定义式如下：

D=(f0-ft)/f0

(13)

式中：f0,ft分别为0时刻、t时时刻组合转子固有频率。

各退化量参数值即为退化数据，对退化数据进行曲线拟合所得退化参数随时间变化的函数即为退化轨迹[17]，见图6，获得组合转子(工作温度873 K)退化轨迹服从指数函数分布，即

D=D1e(-t/D2) +D3

(14)

式中：D1,D2,D3为常数。

图6　组合转子在不同失谐量下的退化轨迹 Fig.6 Degradation path at different mistuning degree

由图6看出，预紧失谐对组合转子退化轨迹影响不大。由式(14)知，随时间增加退化量趋近退化参数D3值;在1×105h,D3在负失谐、谐调、正失谐时分别为0.00656、0.00662、0.00666。

7预紧失谐组合转子性能退化特征分析

拉杆初始预紧不均产生的广义附加力矩相当于给转子施加附加力矩，将造成转子初始弯曲[18]。为研究拉杆松弛所致预紧失谐组合转子退化特征，对其在简单弹性支承下进行不平衡响应分析。轴承支撑刚度为108N/m。结合组合转子几何特性与振型曲线,不平衡响应观测点位置见图7。

图7　激振点与观测点位置 Fig.7 Position of exciting points and observation points

轴向力8F0作用下的轮盘界面刚度K通过虚拟材料层弹性模量表达，将大小为F的附加预紧力施加于拉杆上，对失谐量在-10%～10%内的组合转子进行含预应力模态分析。在此基础上用模态综合法对失谐组合转子进行谐响应分析。获得3000 r/min转速、预紧失谐下组合转子不平衡响应。失谐量为10%的不平衡响应见图8。由图8看出，预紧失谐组合转子一阶振动幅值最大，其中沿组合转子轴向振幅由中间向轴端逐步减小，观测点3处幅值最大。负失谐下组合转子不平衡响应规律相同，取观测点3处振幅进行分析。

图8　失谐的组合转子不平衡响应 Fig.8 Unbalance response about mistuning rotor

图9　组合转子振幅随时间的变化 Fig.9 The amplitude of combined rotor change with time

同前，在温度873K、转速3000 r/min条件下用模态综合法对组合转子进行含预应力的谐响应分析，获得组合转子最大幅值随退化时间变化见图9。由图9看出，随时间增加预紧失谐组合转子响应幅值减小，但远大于预紧谐调下振幅。此因在失谐组合转子退化过程中受预紧降低及预紧失谐两因素耦合作用中预紧失谐起主导作用，失谐量随时间减小对组合转子振幅影响较大。初始预紧失谐程度相同时，随时间增加负失谐对组合转子振动影响较大，在104～105h内负失谐所致不平衡响应幅值为正失谐的1.38～1.66倍。

8拉杆松弛所致组合转子性能退化试验

图10　组合转子实验装置 Fig.10 The experiment equipment of combined rotor

本文建立有限元模型分析组合转子动力学特性，计算中存在一定简化及假设，建立与图1同尺寸实验模型转子，见图10。在不同预紧情况下实测振动模态，验证有限元方法的分析结果。

实验采用锤击法，即用力锤敲击组合转子上某点施加激励，由LMS模态分析仪器记录试件测点响应，经数据处理获得组合转子固有频率。通过测量拉杆轴向拉伸应变获得不同拧紧力矩下拉杆预紧力，采用120Ω电阻式应变片、HX3811静态应变仪，测试分辨率为1 με，误差±2 με。

组装、预紧组合转子过程中用立式组装、对称交叉预紧及分步拉紧三种方式实现拉杆预紧谐调。在预紧谐调基础上拧紧或拧松某根拉杆获得预紧失谐组合转子。本实验取873 K温度下拉杆的等效预紧力，通过调整预紧力值表征拉杆松弛程度，测试获得组合转子弯曲振动频率随时间变化规律，见表3。由表3看出，实验组合转子固有频率与有限元分析结果相差不大，取组合转子频率相对降低量作为退化数据，实验组合转子的退化轨迹与有限元分析结果相差不大。一定程度上可证实本文转子模型的正确性及组合转子性能退化分析结果的可靠性。

9结论

(1)通过所提考虑粗糙界面的预紧失谐组合转子动力学建模方法发现，失谐拉杆随时间增加有趋于谐调趋势；初始失谐量相当情况下随时间增加初始正失谐拉杆预紧力失谐程度小于负失谐。

(2)建立以组合转子频率相对降低量表征性能退化量的定量评估方法，以组合转子频率相对降低量作为组合转子性能退化量参数发现，拉杆松弛引起的组合转子退化量参数符从指数函数分布；预紧失谐对退化量分布影响不大。

表3　实验组合转子在不同预紧力作用下的弯振频率

(3)由预紧失谐组合转子性能退化特征发现，时间增加预紧失谐组合转子响应幅值减小。初始预紧失谐程度相同时，随时间增加负失谐对组合转子振动影响较大，在104～105h范围内负失谐所致不平衡响应幅值为正失谐的1.38～1.66倍。

参考文献

[1]朱启宝, 汪鸿振. LM5000 燃机振动研究[J]. 噪声与振动控制,2006, 26(2): 16-19.

ZHU Qi-bao,WANG Hong-zhen. Vibration analysis of LM5000 gas turbine[J]. Noise and Vibration Control 2006, 26(2): 16-19.

[2]Mohammadi M, Salimi H R. Failure analysis of a gas turbine marriage bolt[J]. Journal of Failure Analysis and Prevention, 2007, 7(2): 81-86.

[3]Castanier M P, Pierre C. Modeling and analysis of mistuned bladed disk vibration: current status and emerging directions [J]. Journal of Propulsion and Power, 2006, 22(2): 384-396.

[4]袁淑霞,张优云,蒋翔俊,等.拉杆失谐模型及其对端面弧齿应力分布的影响[J].哈尔滨工业大学学报,2013,45(5):64-69.

YUAN Shu-xia, ZHANG You-yun, JIANG Xiang-jun,et al. Analysis of bolt preload mistuned model and its impact on stress distribution of curvic couplings[J]. Journal of Harbin Institute of Technology, 2013,45(5):64-69.

[5]Diakunchak I S. Performance degradation in industrial gas turbines[J]. ASME Journal of Engineering for Gas Turbines and Power, 1992, 114:161-168.

[6]Brooks F J. GE gas turbine performance characteristics[R]. GE Power Systems GER-3567H,2003.

[7]Kurz R, Brun K. Degradation in gas turbine systems[J]. Journal of Engineering for Gas Turbines and Power, 2001,123(1):70-77.

[8]Brotherton T, Jahns G, Jacobs J, et al. Prognosis of fault in gas turbine engines[J].IEEE Aerospace Conference Proceedings, 2000(6):163-171.

[9]Li Y G, Nilkitsaranont P. Gas turbine performance prognostic for condition-based maintenance[J]. Applied Energy, 2009(86): 573-584.

[10]Venturini M, Puggina N. Prediction reliability of a statistical methodology for gas turbine prognostics[J].Journal of Engineering for Gas Turbines and Power,2012,134(10):101601.

[11]肖会芳，卲毅敏，徐金梧. 粗糙界面法向接触振动响应与能量耗散特性研究[J]. 振动与冲击, 2014,33(4) : 149-155.

XIAO Hui-fang, SHAO Yi-min, XU Jin-wu. Dynamic response and energy dissipation characteristics for normal contact vibration of a rough interface[J]. Journal of Vibration and Shock,2014,33(4) : 149-155.

[12]李辉光，刘恒，虞烈. 粗糙机械结合面的接触刚度研究[J]. 西安交通大学学报，2011, 45(6): 69-74．

LI Hui-guang, LIU Heng, YU Lie. Study on contact stiffness of rough mechanical joint surface [J]. Journal of Xi’an Jiao Tong University,2011,45(6): 69-74．

[13]廖伯瑜,周新民,尹志宏. 现代机械动力学及其工程应用[M]. 北京：机械工业出版社，2004:243-245.

[14]郭进全,轩福贞,王正东,等. 基于蠕变的高温构件应力松弛损伤模型[J].核动力工程,2009,30(4):9-12.

GUO Jin-quan, XUAN Fu-zhen, WANG Zheng-dong,et al. Creep based stress relaxation damage model for high temperature components[J]. NuclearPower Engineering, 2009, 30(4):9-12.

[15]李玲. 涡轴发动机转子连接螺栓的强度与蠕变寿命研究[D]. 南京：南京航空航天大学, 2008.

[16]于慧臣,吴学仁. 航空发动机设计用材料数据手册[M]. 北京: 航空工业出版社,2010:85-107.

[17]Chao M T. Degradation analysis and related topics: some thoughts and a review[J]. Proc, Natl, Sci. Counc. ROC(A), 1999,23(5):555-566.

[18]Lu Y J, Zhang Y F, Yu Y B, et al. Nonlinear dynamics of flexible rotor system supported on fixed-tilting pad combination journal bearing[J]. Journal of Central South University of Technology, 2011, 18(3): 22-29.