TMD等强度悬臂梁实际应用时的频率精确分析

陈政清+田静莹+黄智文+王嘉兴

摘要：为了确定实际应用中调谐质量阻尼器（TMD）刚度单元的梯形悬臂梁参数，建立了梯形悬臂梁频率的精确计算公式，计算了梯形等强度悬臂梁与三角形等强度悬臂梁频率的误差，利用梯形悬臂梁频率计算公式确定了TMD等强度悬臂梁的设计步骤与程序，给出了工程示例，并使用仿真软件ANSYS进行了验证。结果表明：悬臂梁自由端的宽度小于固定端宽度的12.65%时，梯形等强度悬臂梁与三角形等强度悬臂梁的频率相对误差小于5%；所用程序可以用于确定满足频率精度要求的TMD等强度悬臂梁的参数，对工程实际有较大指导意义。

关键词：调谐质量阻尼器；等强度悬臂梁；固有频率；精确分析；程序设计

中图分类号：U441文献标志码：A

Abstract： In order to determine the parameters of trapezoidal cantilever beam of stiffness element of tuned mass damper （TMD） in practical cases， the exact analytic solution of frequency of trapezoidal cantilever beam was deduced.The error of frequency between triangular equal strength cantilever beam and trapezoidal equal strength cantilever beam was calculated. The design procedure and program of equal strength cantilever beam of TMD using the formula of frequency of trapezoidal cantilever beam was defined. A typical example in engineering field was given and the results were checked with simulation software ANSYS. The results show that when the width of free end is less than 12.65% of the width of fixed end， the error of frequency between them is less than 5%. The designed program can be applied to determine parameters of equal strength cantilever beams of TMD when the accuracy requirements of frequency are met， and it is of great value when applied to the practical cases of engineering.

Key words： tuned mass damper； equal strength cantilever beam； natural frequency； exact analysis； programming

0引言

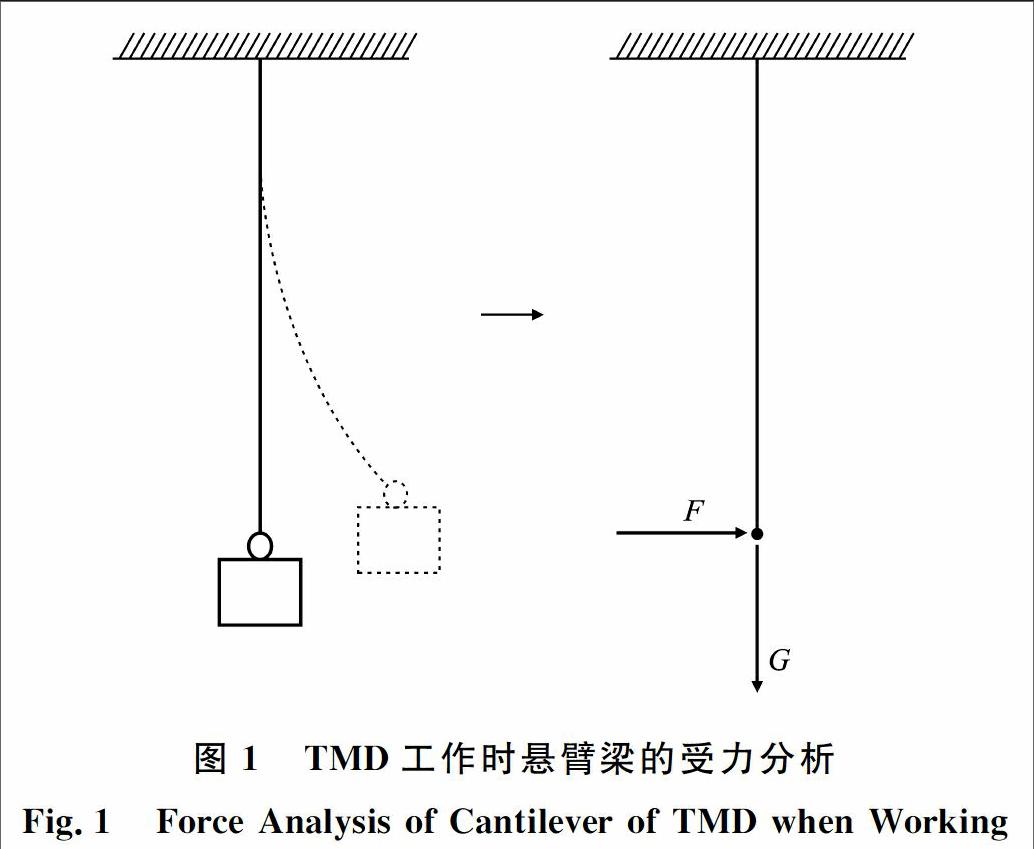
随着土木工程基础理论的发展，结构不单要考虑静力作用，也要满足风荷载和地震荷载等动荷载作用下的振动问题。传统的结构设计仅依靠结构自身的性能，如增加结构刚度、强度、阻尼和改变质量分布来抵抗振动。结构振动控制理论的研究和应用是结构抗振研究的重大突破。根据是否需要外界能源，结构控制方法可以分为以下4种：①被动控制，不需要外部能源，仅依靠控制装置与结构的相互作用提供控制，如调谐质量阻尼器（TMD）和多调谐液体阻尼器（TLD）；②主动控制，需要外部能源提供控制，控制力的大小由前馈外激励和反馈结构的动力响应决定；③半主动控制，所需能源较少，以被动控制为主；④混合控制，如主被动控制[1]。在众多可用的控制装置中，TMD是最常用的控制装置，TMD的形式多种多样。刚度单元为弹簧时，若用弹簧控制竖向刚度，则需要有足够的空间满足弹簧的静力伸长与振动位移（如杨浦大桥一阶竖向弯曲频率为0.286 Hz，弹簧净伸长约为3 m[2]），若用弹簧控制横向刚度，则弹簧不能承受TMD质量单元的重力，质量单元底部还需要有承受重力的构造，构造比较复杂，所以在使用TMD控制结构的横向振动时常使用摆式构造，如台北101大厦抑制风振的TMD使用的钢索[3]和榕江特大桥抑制吊杆振动的TMD使用的等强度悬臂梁[4]都是摆式TMD刚度单元。等强度悬臂梁作为刚度单元时，一是可以控制TMD最大振动对应的应力在疲劳控制应力之内，从而避免往复运动产生疲劳破坏的可能[4]；二是可以最大程度减少材料的使用[5]，更加经济；三是可以同时达到容许应力，减少应力分布不均现象，从而提高安全系数[6]。

目前对于等强度悬臂梁的研究主要集中在将等强度悬臂梁作为高频振动传感器的振动元件、光纤光栅传感器的转换元件，以及广泛利用等强度悬臂梁标定应变测试装置和测力传感器。如1987年耿运贵[7]设计了等强度悬臂梁标定应变片的方法和之后其他学者对等强度标定梁应变的不确定分析和最佳设计方法研究，2009年孙华等[8]推导了三角形等强度悬臂梁的共振频率计算公式，2015年王雷等[9]研究了不同尺寸等强度悬臂梁的自由端挠度量程与作用力量程。

然而，对于实际应用中等强度悬臂梁自振频率的研究却很少，因为实际应用中TMD等强度悬臂梁的自由端必须悬挂质量单元，自由端的宽度不能为0，即等强度悬臂梁的形状不能为三角形。在实际中将三角形等强度悬臂梁自由端加宽后，梁的刚度变大、基频变大。若使用三角形等强度悬臂梁固有频率的简单计算公式来确定符合TMD设计频率的梁的参数，则会与TMD设计频率产生偏差。2014年邱艳宇等[10]研究发现，在三角形悬臂梁的自由端接上一块长度为总长度28%、宽度为固定端宽度45%的矩形板时，其基频与同样尺寸的三角形悬臂梁的基频相差44%。王文熙[11]研究发现，频率偏离对TMD的减振效果有很大影响，所以当自由端加宽时，悬臂梁的各个参数都需要进一步调整，传统的调整方法是使用有限元软件人为逼近，若是施工中存在反复修改，则人为逼近非常麻烦。因此，本文首先研究了实际使用的梯形悬臂梁自由端加宽多少时其频率与三角形梁的频率误差小于限值，即可以使用三角形梁频率计算公式来确定梁的参数；其次，推导了梯形悬臂梁频率的精确计算公式，以及应用此公式设计TMD刚度单元时的参数确定方式与程序；最后，提供了TMD等强度悬臂梁刚度单元的设计示例，并用仿真软件ANSYS对比验证了梯形等强度设计方法的精确性。