基于微分求积法的印刷运动薄膜动力稳定性分析
2016-01-15武吉梅,陈媛,王砚等
第一作者武吉梅女,博士,教授,博士生导师,1963年10月生
基于微分求积法的印刷运动薄膜动力稳定性分析
武吉梅,陈媛,王砚,武秋敏
(西安理工大学,西安710048)
摘要:以印刷运动薄膜为研究对象进行横向振动特性及稳定性研究。建立抛物线型变密度运动薄膜计算模型。用微分求积法对运动薄膜横向振动方程进行离散,获得运动薄膜的复特征值方程。通过数值求解获得系统无量纲复频率与运动速度、密度系数、薄膜张力比的关系曲线,确定密度系数与临界速度的函数关系,分析密度系数、薄膜张力比对薄膜振动特性影响。结果表明,密度系数及张力比对薄膜稳定性有重要影响。
关键词:印刷运动薄膜;动力稳定性;微分求积法;抛物线变密度
基金项目:国家自然科学基金(11272253,11202159);陕西省自然科学基金(2014JM7290);陕西省重点实验室项目(13JS081)
收稿日期:2015-01-26修改稿收到日期:2015-03-10
中图分类号:TS803.6
文献标志码:A
DOI:10.13465/j.cnki.jvs.2015.20.010
Abstract:A printing moving membrane was concerned and its transverse vibration characteristics and dynamic stability were analyzed. A calculation model of the moving membrane with parabolic density distribution was established. The transverse vibration equation of the printing membrane was discretized using the differential quadrature method, and the complex eigen value equation was obtained. The relation curves of the first three dimensionless complex frequencies versus the dimensionless velocity, the density coefficient and the tension ratio were derived by numerical calculation. The functional relationship between the density coefficient and the critical speed was determined. The effects of density coefficient and tension ratio on vibration characteristics of the membrane were discussed. The numerical results show that the density coefficient and the tension ratio have important impacts on the stability of moving membrane. The study provides a theoretical basis for optimizing the structure of printing press and improving the working stability of high-speed moving membranes.
Dynamic stability of printing moving membrane based on differential quadrature method
WUJi-mei,CHENYuan,WANGYan,WUQiu-min(Xi’an University of Technology, Xi’an 710048, China)
Key words:printing moving membrane; dynamic stability; differential quadrature method;parabolic density distribution
卷筒纸印刷机纸带、凹版印刷机薄膜、生产线的纸张等均可模化为轴向运动的薄膜。薄膜作为承印材料广泛用于印刷包装领域。高速运动的料膜在印刷过程中横向振动及由振动引发的“皱褶”现象会严重影响印品的套印精度,从而影响其质量。诸多场合薄膜密度非恒定,如印刷纸带或PET膜等。印刷中印版据图文分布进行润湿、着墨,通过橡皮滚筒、压印滚筒对滚将油墨转移至承印物。该油墨及润版液必会引起料膜面密度变化;而承印物厚度不均匀也会使面密度发生变化。面密度不均匀会影响薄膜的振动特性、降低印刷的稳定性,进而影响印品质量。因此,研究变密度运动薄膜的横向振动特性,对有效控制印刷过程中薄膜振动、提高印品套印精度具有重要意义。
近年来,轴向运动系统横向振动及稳定性研究已取得较大成果。陈立群等[1-4]分别研究轴向运动弦线、梁及薄板的横向非线性振动问题,并就不同研究对象分析其稳态响应过程。王冬梅等[5]用微分求积数值方法求解轴向加速粘弹性梁的横向振动控制方程。周银锋等[6]研究轴向运动粘弹性板的横向振动特性。Shin等[7]通过研究轴向运动薄膜面外振动动力特性,发现薄膜固有频率及振动模型受运动速度、边界条件、薄膜张力比及长宽比影响。Kulachenk等[8-9]对薄膜非线性动力学行为深入研究,并用算例进行验证。赵凤群等[10]研究四边固支运动矩形薄膜的振动特性。Wu等[11]研究加速运动矩形纸带的稳定性问题,确定纸带动力不稳定及稳定性区域,并讨论系统参数对不稳定区域影响。Nguyen等[12-13]分别研究轴向运动纸带、薄膜在给定速度下的稳定性及横向振动控制问题。Ma等[14]用次最优控制法分析变密度运动纸带的振动控制问题。
以上研究多为恒定密度下轴向运动体的振动特性及控制问题。本文以印刷运动薄膜为研究对象,建立抛物线型变密度印刷薄膜的振动微分方程。用微分求积法计算变密度薄膜的横向振动,获得系统无量纲复频率与运动速度、密度系数、薄膜张力比的关系曲线,确定密度系数与临界速度关系。分析密度系数、薄膜张力比对薄膜振动特性影响。
1振动模型建立
变密度印刷运动薄膜计算模型见图1。其中图1 (a)、(b)分别为变密度印刷薄膜的力学模型及密度变化规律。将印刷过程中两对滚筒(或辊子)间支承的一段运动薄膜简化为数学模型(图1(a)),并对此段薄膜进行受力分析。
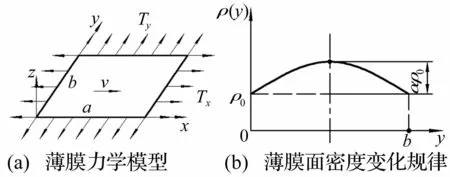
图1 薄膜力学模型及面密度变化规律 Fig.1 Mathematical model and density change rule

(1)
设薄膜振动时所受外力F(x,y,t)沿z向,得运动薄膜横向振动微分方程[15]为
(2)
不考虑横向外力作用即F(x,y,t)=0,将变密度式(1)代入式(2),整理得抛物线型变密度印刷运动薄膜的横向振动微分方程为
(3)
引入无量纲量
(4)
将式(3)化为无量纲形式,即
(5)
设方程(5)的解为
w(ξ,η,τ)=W(ξ,η)ejωτ
(6)
将式(6)代入式(5),得抛物线型变密度印刷薄膜的横向振型微分方程为
(7)

印刷运动薄膜边界条件为
(8)
2复特征方程
据微分求积法[16]引入N×N(N=9)个网点,网点划分形式为
(9)
未知数各阶偏导数可表示为
(10)
各阶权系数值计算式为
(11)
(12)
对式(7)用微分求积法建立复特征值方程,微分求积形式为
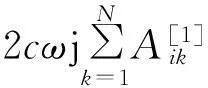
4α(η-η2)ω2Wij=0
(13)
边界条件的微分求积形式为
(14)
将式(13)、(14)合并成矩阵形式可构成广义特征值问题,其特征方程为
(15)
式中:R,G,K为矩阵,含薄膜张力比λ、无量纲速度c、密度系数α、长宽比μ等参数。
3计算结果及分析
密度系数α=0时变密度印刷运动薄膜振动方程退化为密度均匀不变的运动薄膜横向自由振动方程。取α=0,c=0,λ=1,长宽比分别为μ=1及2,计算运动薄膜前3阶无量纲振动复频率,结果见表1。由表1知,利用微分求积法所得振动频率值与文献[17]解相吻合,表明用微分求积法求解运动薄膜的横向振动可行、有效。

表1 横向振动频率解的比较
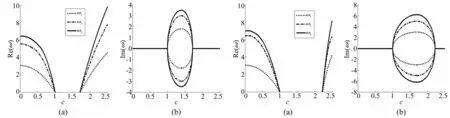

图2 无量纲复频率与速度关系(λ=0.5,μ=2,α=0)Fig.2Dimensionlesscomplexfrequencyvariedwithdimensionlessvelocity图3 无量纲复频率与速度关系(λ=1,μ=2,α=0)Fig.3Dimensionlesscomplexfrequencyvariedwithdimensionlessvelocity
张力比λ=1、长宽比μ=2、密度系数分别为α=0.4、α=0.7、α=1.0时变密度薄膜第1阶无量纲复频率实部、虚部与速度关系变化曲线见图4。由图4看出,随密度系数增大第1阶模态发散失稳的临界速度不断减小;第1阶模态重新趋于稳定状态的速度不断提前。α=1.0时临界速度提前到cr=0.71。
张力比为λ=0.5、λ=0.8、λ=1.0(α=0.4、μ=2)时第1阶无量纲复频率实部与速度关系曲线见图5。由图5看出,张力比增大对三条曲线变化趋势影响较小,即张力比对临界速度及第1阶复频率大小影响较小。
张力比为λ=0.5、λ=1时密度系数与3阶模态临界速度关系曲线见图6。由图6看出,密度系数增大3阶模态临界速度逐渐减小,两条曲线基本重合,说明张力比对临界速度影响较小。


图4 第1阶无量纲复频率与速度关系(λ=1,μ=2)Fig.4Dimensionlesscomplexfrequencyvariedwithdimensionlessvelocity图5 第1阶无量纲复频率实部与速度关系(α=0.4、μ=2)Fig.5Dimensionlesscomplexfrequencyvariedwithdimensionlessvelocity图6 密度系数与前3阶模态临界速度关系Fig.6Relationshipbetweendensitycoefficientandcriticalspeed
4结论
用微分求积法对面密度以抛物线规律变化的印刷运动薄膜振动特性及稳定性进行研究,并通过退化验证该方法的可行性及有效性。结论如下:
(1)密度系数α=0时前3阶无量纲复频率实部随无量纲速度增大不断减小,阶数越高,初始复频率实部值越大;对薄膜稳定工作区中任意相同无量纲速度,张力比增大高阶复频率值不断增大,薄膜不稳定区域持续范围随之增大。
(2)α>0时,在密度系数、长宽比相同情况下,张力比对临界速度及第1阶复频率大小影响较小。对相同张力比、长宽比薄膜,临界速度随密度系数增大而减小,系统重新趋于稳定状态的速度亦越小,说明此时薄膜的稳定性态变差。
(3)本文计算结果可用于确定印刷机械设计、制造及使用中安全稳定工作速度区间,同时亦为进一步优化印刷机结构提供理论依据。
参考文献
[1]吴俊,陈立群. 轴向变速运动弦线的非线性振动的稳态响应及其稳定性[J]. 应用数学和力学,2004,25(9):917-925.
WU Jun, CHEN Li-qun. Steady-state responses and their stability of nonlinear vibration of an axially accelerating string [J]. Applied Mathematics and Mechanics,2004, 25(9): 917-925.
[2]丁虎,陈力群. 轴向运动粘弹性梁横向非线性受迫振动[J]. 振动与冲击,2009,28(12):128-131.
DING Hu, CHEN Li-qun.Transverse non-linear forced vibration of axially moving viscoelastic beam [J]. Journal of Vibration and Shock,2009,28(12):128-131.
[3]熊杨柳,张国策,丁虎,等. 粘弹性屈曲梁非线性内共振稳态周期响应[J]. 应用数学和力学,2014,35(11):1188 -1196.
XIONG Yang-liu, ZHANG Guo-ce, DING Hu,et al. Steady-state periodic responses of a viscoelastic buckled beam in nonlinear internal resonance[J]. Applied Mathematics and Mechanics, 2014, 35(11):1188-1196.
[4]唐有绮,陈立群. 面内平动黏弹性板非线性振动的内-外联合共振[J]. 应用数学和力学,2013,34(5):480-487.
TANG You-qi, CHEN Li-qun.Internal-external combination resonance of nonlinear vibration of in-plane translating viscoelastic plates[J]. Applied Mathematics and Mechanics, 2013, 34(5): 480-487.
[5]周银锋,王忠民. 轴向运动粘弹性板的横向振动特性[J]. 应用数学和力学,2007, 28(2): 191-199.
ZHOU Yin-feng, WANG Zhong-min.The transverse vibration characteristics of the axially moving viscoelastic plate[J]. Applied Mathematics and Mechanics,2007, 28(2): 191-199.
[6]王冬梅,张伟,刘燕. 用微分求积法分析轴向加速粘弹性梁的非线性动力学行为[J]. 动力学与控制学报,2013, 11(1):41-45.
WANG Dong-mei, ZHANG Wei, LIU Yan. Analysis on nonlinear dynamics of an axially accelerating viscoelastic beam using DQM [J]. Journal of Dynamics and Control, 2013, 11(1): 42-45.
[7]Shin C, Chung J, Kim W. Dynamic characteristics of the out-of-plane vibration for an axially moving membrane [J].Journal of Sound and Vibration, 2005,286:1019-1031.
[8]Kulachenko A, Gradin P, Koivurova H. Modeling the dynamical behaviour of a paper webpart I [J]. Computers and Structures, 2007, 85(1): 131-147.
[9]Kulachenko A, Gradin P, Koivurova H. Modeling the dynamical behaviour of a paper webpart II[J]. Computers and Structures, 2007, 85(2): 148-157.
[10]赵凤群,王忠民. 运动矩形薄膜的非线性振动分析[J]. 机械科学与技术,2010,29(6):768-771.
ZHAO Feng-qun,WANG Zhong-min. Nonlinear vibration analysis of a moving rectangular membrane[J]. Mechanical Science and Technology for Aerospace Engineering, 2010, 29(6): 768-771.
[11]Wu Ji-mei, Wu Qiu-min, Ma Li-e,et al. Parameter vibration and dynamic stability of the printing paper web with variable speed [J]. Journal of Low Frequency Noise, Vibration and Active Control, 2010, 29 (4): 281-291.
[12]Nguyen Q C, Hong K S. Stabilization of an axially moving web via regulation of axial velocity[J]. Journal of Sound and Vibration, 2011, 330(20): 4676-4688.
[13]Nguyen Q C, Hong K S. Transverse vibration control of axially moving membranes by regulation of axial velocity [J]. IEEE Transactions on Control Systems Technology, 2012, 20(4): 1124-1131.
[14]Ma Li-e, Wu Ji-mei, Mei Xue-song,et al. Active vibration control of moving wed with varying density[J]. Journal of Low Frequency Noise, Vibration and Active Control, 2013, 32(4): 323-334.
[15]Wu Ji-mei, Lei Wen-jiao, Wu Qiu-min,et al. Transverse vibration characteristics and stability of a moving membrane with elastic supports[J]. Journal of Low Frequency Noise, Vibration and Active Control, 2014, 33(1): 65-78.
[16]王永亮. 微分求积法和微分求积单元法-原理与应用[D]. 南京:南京航空航天大学,2001.
[17]Timoshenko S P, Young D H, Weaver W. Vibration problems in engineering[M]. New York:John Wiley & Sons, Inc., 1974.


