基于反馈线性化的非线性悬架系统振动状态观测

第一作者陈思忠男，教授，博士生导师，1958年10月生

通信作者赵玉壮男，教授，讲师，1982年11月生

基于反馈线性化的非线性悬架系统振动状态观测

陈思忠，卢凡，吴志成，杨林，赵玉壮

(北京理工大学机械与车辆学院，北京100081)

摘要：针对悬架系统非线性特性提出反馈线性化卡尔曼滤波算法。基于微分几何理论，通过求解坐标变换，将车辆非线性振动模型变换成可观测标准型，实现系统精确反馈线性化；采用线性卡尔曼滤波算法，针对变换的线性系统设计观测器，通过坐标逆变换获得原非线性系统的状态观测值。仿真结果表明，该算法能提高车辆振动状态观测精度、降低运算量。

关键词：状态观测；反馈线性化；非线性悬架；振动

基金项目：国家自然科学基金(51205021)

收稿日期：2014-05-16修改稿收到日期：2014-09-30

中图分类号:U461.4；U463.3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.20.003

Abstract:Aiming at the nonlinearity of suspension system, a feedback linearization Kalman filter algorithm was proposed. Based on the differential geometry theory, the nonlinear vehicle vibration model was transformed into a certain observable normal form via the change of state coordinates. Based on the obtained linearized system, an observer was designed by using Kalman filter algorithm. Finally the estimated states of the nonlinear system were obtained through inverse transformation. The simulation results show that compared with the extended Kalman observer, the proposed algorithm can improve the observation accuracy of vehicle vibration states and reduce computational complexity.

Vibration state estimation of nonlinear suspension system based on feedback linearization

CHENSi-zhong,LUFan,WUZhi-cheng,YANGLin,ZHAOYu-zhuang(School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China)

Key words:state estimation; feedback linearization; nonlinear suspension; vibration

虽悬架系统控制策略得到飞速发展，但大多需整车振动状态已知，难以由传感器获得，解决此问题的常用方法为建立车辆振动状态观测器[1]。目前车辆振动状态观测算法研究主要针对线性悬架车辆系统[2-4]，而实际车辆悬架系统一般具有非线性特性，若将实际车辆简化为线性系统，基于线性模型设计振动状态观测器，虽可简化设计，但存在观测精度低、易失效等缺陷，影响智能悬架系统控制效果。因此，研究悬架系统非线性特性、设计车辆振动状态观测器，对提高悬架控制性能具有重要意义。

线性系统状态观测算法已较成熟，而非线性系统，因其本身的复杂性无适用所有非线性系统的万能方法，需对不同对象用不同的非线性状态观测算法[5]。对工程中广泛存在的系统非线性特性，较有效的处理方式即进行线性化处理，采用线性方法解决。传统的线性化方法在平衡点附近将系统模型进行级数展开并舍弃高次项，获得线性近似，但在工作平衡点附近展开只能反映系统此处特性，随工作区域扩大，舍弃高次项所致误差会逐渐增大[6]。而用微分几何理论研究非线性系统的精确线性化获得一定发展[7]。该方法主要思想为通过寻找合适的非线性坐标变换，将原系统变换成可观测的标准型，再利用线性误差动态构造观测器，经坐标逆变换获得原非线性系统的状态观测[8]。

本文针对1/4车辆非线性悬架振动系统，基于微分几何理论分析论证其可观测性及观测器线性化问题的可解性。采用反馈线性化卡尔曼滤波算法设计非线性悬架系统振动状态观测器，并仿真验证该观测算法对车辆振动状态的观测效果及运算效率。

1非线性悬架系统建模

1.11/4车辆振动模型

图1为1/4车辆振动模型，主要为两自由度振动，即车身质心、车轮质心垂向振动。图中mb为等效车身质量；mw为等效车轮质量；zg，zb，zw分别为路面激励、车身及车轮垂向位移。

系统坐标原点取在静力平衡位置，根据牛顿第二定律，则描述1/4车辆运动的微分方程为

(1)

图1　1/4车辆模型示意图 Fig.1 Schematic diagram of quarter-car model

式中：Fs(·)为悬架弹性力函数，弹簧伸张时弹性力为正；Fd(·)为悬架阻尼力函数，减振器伸张行程阻尼力为正；kt为轮胎刚度系数。

本文悬架系统采用空气弹簧及双向作用筒式减振器。空气弹簧的气囊、活塞直径分别为D、d，气囊容积等效高度为h，气囊截面积A及活塞工作有效作用面积Aα为

A=πD2/4

(2)

Aα=π(D2+d2)/8

(3)

空气弹簧的动态弹性力[9-10]为

(4)

式中：Δz=zb-zw为空气弹簧伸张位移量；r=1.4为气体多变指数；p0=1.01×105Pa为大气压力；g=9.81 m·s-2为重力加速度。

据减振器阻尼力试验数据，用分段线性函数表达式近似，确定非参数化模型为

(5)

式中：vs为伸张行程开阀速度；vy为压缩行程开阀速度；cs1，cs2为伸张行程阻尼系数；cy1，cy2为压缩行程阻尼系数。

至此，已建立空气悬架非线性弹性力及阻尼力模型，即1/4车辆非线性悬架振动模型。

1.2非线性悬架系统状态空间表示

对1/4车辆非线性悬架系统，选状态变量为

(6)

以悬架相对运动速度、位移为测量变量，则有

(7)

式(1)的状态空间形式为

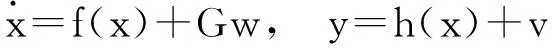
(8)

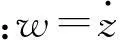
及

为非线性函数及系数矩阵。

2非线性悬架振动状态观测系统反馈线性化

据微分几何理论，系统满足一定条件时可通过寻找合适的非线性坐标变换将原非线性系统精确反馈线性化[11]。既可保证系统模型的准确性，亦可用理论成熟的线性观测算法。

式(8)为无输入多输出随机系统，满足可精确反馈线性化充要条件时[12]通过反馈线性化获得可观测标准型为

(9)

2.1系统可观测性验证

通过计算输出函数各阶李导数对x的偏导，判断系统可观矩阵是否满秩，验证非线性悬架系统的可观测性。

2.1.1输出函数各阶李导数对x偏导计算

输出函数h1各阶李导数对x的偏导数为

dh1=[1,-1,0,0]

(10)

(11)

(12)

(13)

式中：

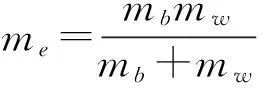
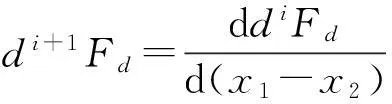
输出函数h2各阶李导数对x的偏导数为

dh2=[0,0,1,0]

(14)

(15)

2.1.2系统可观测性判断

(16)

使可观矩阵

(17)

满秩，即rankQ=n。

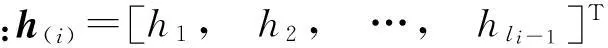
据式(8)的具体形式，可验证序列维数k=3、且l0=2、l1=1、l2=1时，可观矩阵Q满秩。因此，该非线性悬架系统是可观测的，可观指数为{2,1,1}。

2.2反馈线性化

通过验证系统能精确反馈线性化充要条件求解满足精简对偶Brunovsky形式的可观对(A,C)，进而求解坐标变换偏导数，积分获得坐标变换。

2.2.1可观对(A,C) 求解

记

hⅠ,0=[h1,h2]T，hⅠ,1=h1，hⅠ,2=h1，

hⅡ,0=∅，hⅡ,1=h2，hⅡ,2=h2

(18)

(19)

将式(10)～式(15)代入式(18)、(19)，可证明

(20)

据文献[12]，式(20)成立，坐标变换的偏导有解使C1为单位矩阵，即

(21)

由可观指数{2,1,1}得

(22)

精简对偶Brunovsky形式的可观对(A,C)为

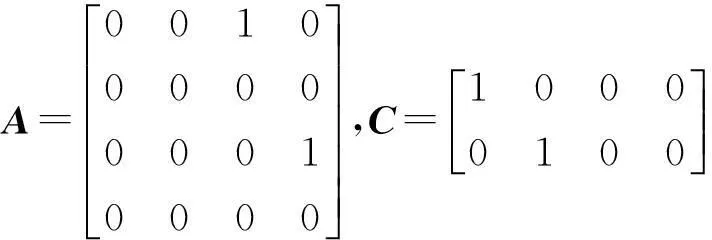
(23)

2.2.2坐标变换偏导数求解

记x=X(ξ)为非线性系统到可观测标准型的坐标变换，则必满足等式

(24)

据广义逆矩阵理论[13]，方程组(24)的通解为

(25)

式中：(·)-为矩阵(·)的任意{1}-逆，满足(·)×(·)-(·)=(·)；Zi为与gi维数相同的任意矩阵。

据式(8)的具体形式计算得gi为

(26)

式中：z22，z42为矩阵Z1第2行第2列元素、第4行第2列元素。

由式(26)得坐标变换的偏导数为

(27)

2.2.3坐标变换求解

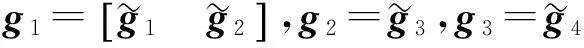
(28)

由于式(28)成立，∂X/∂ξ可积，故得坐标变换为

(29)

进而得映射为

(30)

至此，非线性悬架振动状态观测系统的反馈线性化已完成。

3反馈线性化卡尔曼滤波观测器设计

3.1观测器设计

考虑系统的过程及测量噪声，得含噪声的可观测标准型为

(31)

式中：wξ为过程噪声；B为过程噪声的系数矩阵；vξ为测量噪声。

对比原系统式(8)知，测量噪声由系统决定，与坐标变换无关，故测量噪声为

vξ=v

(32)

对坐标变换的线性系统设计卡尔曼滤波观测器，需确定过程噪声wξ及系数矩阵B。为确定坐标变换后系统过程噪声，设测量变量无误差，即b(y)=b(Cξ)。对比式(8)得

(33)

式中：B1=[0,0,-kt/mw,0]T为系数矩阵。

考虑实测变量含噪声，即b(y)=b(Cξ+vξ)，则

(34)

式中：

综合以上分析，令过程噪声为

(35)

取过程噪声的常系数矩阵为

(36)

式中：dFs0为悬架刚度系数；dFd0为悬架阻尼系数。

至此，已确定随机线性系统式(31)所有变量及系数矩阵。由于线性系统系数矩阵为时不变，当过程、测量噪声满足平衡假设时，可采用稳态卡尔曼滤波算法设计观测器对状态变量ξ进行观测，即

(37)

通过坐标变换求得原坐标下状态变量x的观测值，完成1/4车辆非线性悬架振动状态观测器设计。

3.2仿真对比

3.2.1随机路面仿真

在Matlab仿真环境中对所建1/4车辆非线性悬架模型，用反馈线性化卡尔曼滤波观测器(FLKF)及扩展卡尔曼滤波观测器(EKF)进行车辆振动状态观测。仿真车辆、空气弹簧及减振器参数见表1。

表1　1/4车辆模型仿真参数

对车辆以10 m/s驶过B级随机路面工况进行仿真，结果见图2。由图2看出，反馈线性化卡尔曼滤波观测器能有效观测车身、车轮振动速度及悬架相对运动速度以及车身振动加速度，而扩展卡尔曼滤波观测器观测精度较差。

振动状态观测精度定量分析结果见表2。由表2可知，反馈线性化卡尔曼滤波观测器对车身、车轮振动速度观测精度明显优于扩展卡尔曼滤波观测器，对悬架相对运动速度及车身振动加速度观测精度亦较高。在Matlab仿真环境下，扩展卡尔曼滤波观测器平均一次迭代运算消耗时间为0.141 ms，而反馈线性化卡尔曼滤波观测器为0.087 ms，仅为前者的62%。因此，反馈线性化卡尔曼滤波观测器运算量小于扩展卡尔曼滤波观测器。反馈线性化卡尔曼滤波观测器的观测精度及运算速度均优于扩展卡尔曼滤波观测器。

表2　非线性悬架系统振动状态观测精度(随机路面工况I)

对车辆以20 m/s驶过C级随机路面工况进行仿真，结果见图3及表3。仿真结果表明，随机路面激励变化后反馈线性卡尔曼滤波观测器仍优于扩展卡尔曼滤波观测器，表明非线性悬架系统振动状态观测算法能适应不同随机路面。

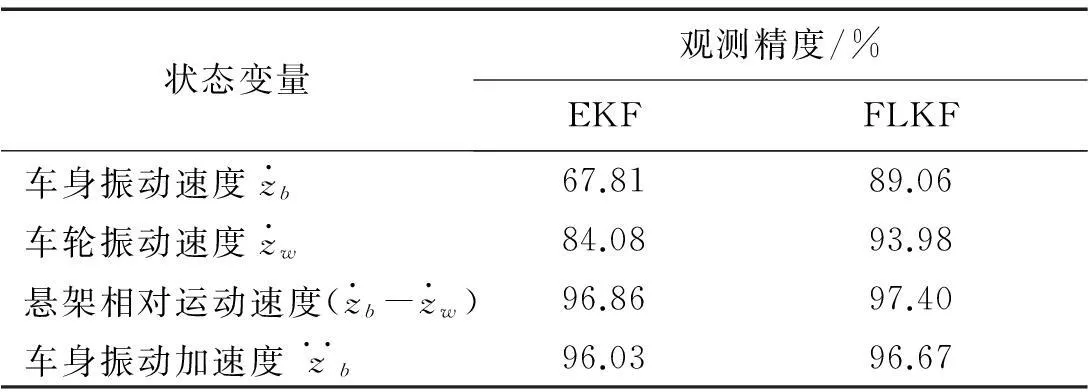
表3　非线性悬架系统振动状态观测精度(随机路面工况II)

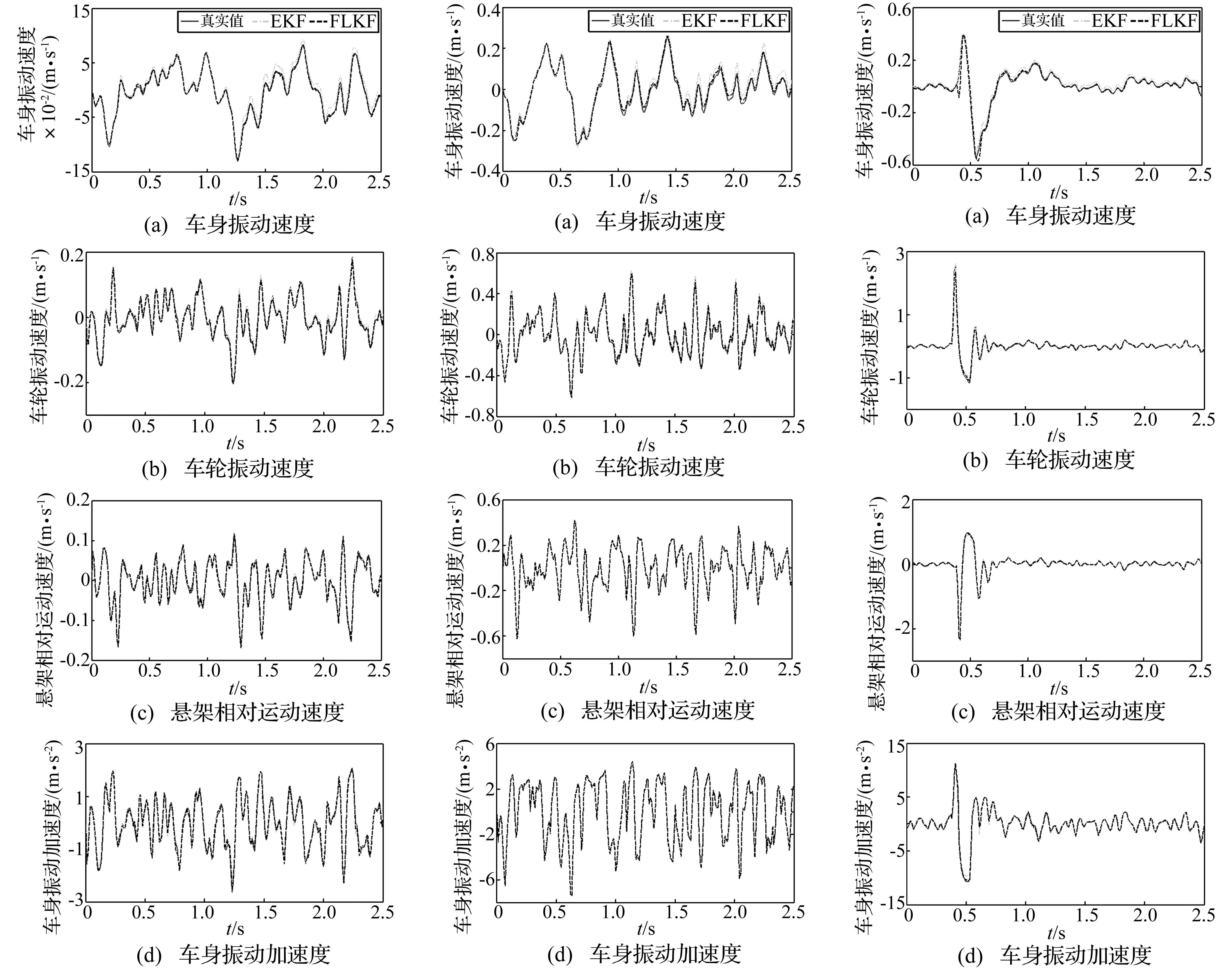
图2 非线性悬架系统振动状态观测(随机路面工况Ⅰ)Fig.2Vibrationstateestimationofnonlinearsuspensionsystem(randomroadexcitationcaseⅠ)图3 非线性悬架系统振动状态观测(随机路面工况Ⅱ)Fig.3Vibrationstateestimationofnonlinearsuspensionsystem(randomroadexcitationcaseⅡ)图4 非线性悬架系统振动状态观测(脉冲路面)Fig.4Vibrationstateestimationofnonlinearsuspensionsystem(impulseroadexcitation)

3.2.2脉冲路面

仿真1/4车辆系统以10 m/s车速通过固定于B级随机路面的减速带工况，结果见图4。仿真曲线表明，车辆刚开始通过减速带时反馈线性化卡尔曼滤波观测器所得车身振动速度存在一定误差，但该观测器能迅速修正该误差；车辆完全通过减速带回到随机路面后，观测值能准确反映真实状态。而扩展卡尔曼滤波观测器虽能在车辆刚遇减速带时较准确观测车身振动速度，但产生的误差不能消除，使车辆完全通过减速带回到随机路面后观测值与真实状态存在固定偏差。较扩展卡尔曼滤波算法，反馈线性化卡尔曼滤波算法对车轮振动速度、悬架相对运动速度及车身振动加速度观测精度较高。

4结论

(1)针对悬架系统非线性特性提出非线性悬架系统振动状态观测算法。基于微分几何理论，通过坐标变换求解，实现非线性系统的精确反馈线性化，并用卡尔曼滤波算法设计状态观测器。

(2)通过坐标逆变换获得原非线性系统状态观测值。较扩展卡尔曼滤波观测器，反馈线性化卡尔曼滤波观测器观测精度更好、运算效率更高。

参考文献

[1]杨林,陈思忠,赵玉壮,等．油气悬架整车的振动状态观测器设计[J]．汽车技术,2011 (8):17-21．

YANG Lin,CHEN Si-zhong, ZHAO Yu-zhuang, et al. Design of vehicle vibration state observer for hydro-pneumatic suspension[J]. Automobile Technology, 2011(8): 17-21.

[2]卢凡,陈思忠,刘畅,等．基于Kalman滤波器的车辆振动速度估计[J]．振动与冲击,2014,33(13):111-116．

LU Fan, CHEN Si-zhong, LIU Chang, et al. Vehicle vibration velocity estimation based on Kalman filter[J]. Journal of Vibration and Shock, 2014, 33(13): 111-116.

[3]Cuadrado J, Dopico D, Perez J A, et al. Automotive observers based on multibody models and the extended kalman filter[J]. Multibody System Dynamics, 2012, 27(1): 3-19.

[4]Doumiati M, Victorino A, Lechner D, et al. Observers for vehicle tyre/road forces estimation: experimental validation [J]. Vehicle System Dynamics, 2010, 48(11): 1345-1378.

[5]贾秀芹,刘允刚．一类更一般Lipschitz非线性系统的观测器设计[J]．山东大学学报:工学版,2007,37(2):113-120．

JIA Xiu-qin, LIU Yun-gang. Observer design for a class of more general Lipschitz nonlinear systems[J]. Journal of Shandong University:Engineering Science,2007,37(2):113-120.

[6]宾洋．车辆走停巡航系统的非线性控制研究[D]．北京：清华大学,2006．

[7]李殿璞．非线性控制系统理论基础[M]．哈尔滨：哈尔滨工程大学出版社,2006．

[8]彭宇．非线性智能观测器及其应用研究[D]．杭州：浙江大学,2000．

[9]孙博．乘用车空气悬架刚度与阻尼的匹配研究[D]．北京：北京理工大学,2012．

[10]成小霞,李宝仁,杨钢,等．囊式空气弹簧载荷建模与实验研究[J]．振动与冲击,2014,33(17):80-84．

CHENG Xiao-xia, LI Bao-ren, YANG Gang, et al. Modeling and tests for load of a cystiform air spring[J]. Journal of Vibration and Shock, 2014, 33(17): 80-84.

[11]Isidori A,著．王奔,庄圣贤,译．非线性控制系统(第3版) [M].北京:电子工业出版社,2012．

[12]Hou M, Pugh A C. Observer with linear error dynamics for nonlinear multi-output systems[J]. Systems & Control Letters, 1999, 37(1): 1-9.

[13]陈永林．广义逆矩阵的理论与方法[M]．南京：南京师范大学出版社,2005．