基于相移陷波器的磁轴承不平衡振动全频自适应控制

第一作者崔培玲女，博士，副教授，1975年4月生

基于相移陷波器的磁轴承不平衡振动全频自适应控制

崔培玲1,2，赵光再1,2，房建成1,2，李海涛1,2

(1. 北京航空航天大学 仪器科学与光电工程学院，北京100191； 2. 惯性技术重点实验室，北京100191)

摘要：为全转速范围内消除磁悬浮转子不平衡质量产生的不平衡振动力，提出基于相移陷波器的不平衡振动全频自适应控制方法。直接以构造的轴承力作为相移带通滤波器输入，将滤波器输出反馈至控制系统构成相移陷波器，达到消除振动力目的。该过程无需考虑功放低通特性对同频成分影响；通过对系统灵敏度函数理论分析，在不同转速下自适应调节相移角，实现全转速范围内系统稳定。结果表明，该方法能在全频范围内有效地消除同频轴承力。

关键词：磁悬浮转子；不平衡振动；相移陷波器；全频

基金项目：国家自然基金(61121003, 61203112)；国家民用航天预研项目

收稿日期：2014-04-18修改稿收到日期：2014-09-16

中图分类号:TH133

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.20.004

Abstract:The mass unbalance of high-speed magnetically suspended rotor causes unbalance force, which induces synchronous vibration. To suppress the vibration effectively within the operating speed range, a method based on a phase-shift notch filter was proposed. The control strategy of the method is that the magnetic bearing force was calculated and taken as the input of the phase-shift band-pass filter and the output of the filter was fed back to the original system, in which the low-pass characteristic of power amplifier doesn’t need to be considered. Meanwhile, based on the theoretical analysis on the sensitivity function of the overall control system, a stable system in the rotating speed range was achieved based on the adaptive adjustment of phase shift in the band-pass filter with respect to rotor speed. The experimental results show the effectiveness of the proposed approach, which can reduce the synchronous magnetic bearing force within the whole frequency range.

Adaptive control of unbalance vibration for magnetic bearings based on phase-shift notch filter within the whole frequency range

CUIPei-ling1,2,ZHAOGuang-zai1,2,FANGJian-cheng1,2,LIHai-tao1,2(1. School of Instrumentation Science and Optoelectronics Engineering, Beihang University, Beijing 100191, China；2. Science and Technology on Inertial Laboratory, Beijing 100191, China)

Key words:magnetically suspended rotor; unbalance vibration; phase-shift notch filter; whole frequency range

磁轴承作为无接触支承结构，具有无摩擦、无需润滑、支承刚度主动可控等特点[1-2]在高速电机、分子泵及航天器姿态控制等领域应用广泛[3-5]。磁悬浮转子因受限加工精度存在残余不平衡质量在高速旋转下产生的不平衡力通过基座传递到外部机构易引起振动、噪声。利用磁轴承主动可控特点可对该振动力进行消除，实现零同频振动控制。

消除磁悬浮转子振动力已有诸多研究，主要有两种实现方式：①以转子惯性主轴为控制目标，使转子绕惯性主轴转动，消除不平衡振动力；②直接以同频振动力或力矩为目标，通过消除同频力或力矩实现。第一种需辨识出转子惯性轴相对参考坐标系位置[6]，抑制效果主要取决于惯性主轴位置的辨识精度。不平衡量较小时传感器安装及检测误差会使其抑制效果不明显。第二种通过在磁悬浮转子系统控制回路中加入算法，消除控制电流、位移中同频成分。Shi等[7]采用最小均方(Least Mean Square, LMS)算法，通过产生等增益、反相位的同频信号，前馈补偿同频电流，实现同频电流刚度力消除，但该方法未考虑位移刚度力产生的振动，且因LMS算法步长固定，无法兼顾系统稳定性及收敛速度要求，仅适用某特定转速范围。Bi等[8]用重复学习算法通过自适应调节学习增益，虽能实现大转速范围内对同频电流的抑制，但仅消除同频电流刚度力，未消除同频位移刚度力，近似零同频振动控制。刘彬等[9]在电流环中加入同频位移刚度力补偿，实现同频振动力消除，并在低转速下用高转速辨识出的转子惯性轴位置消除低转速的同频振动力，达到整个工作频率范围内对同频力的有效抑制；但该文献并未考虑功放的低通特性对同频位移刚度力前馈补偿效果影响。而转速会存在检测误差，开环补偿的相位误差会随时间逐渐积累，补偿效果逐渐降低。针对功放的低通特性，魏彤等[10]通过离线测试获得磁轴承功放参数，在恒定工作转速下对位移刚度力前馈补偿中功放导致的同频成分幅值衰减及相位滞后进行补偿。而功放幅值、相位随转速变化，且随温度等环境影响产生系统参数摄动，在全转速下采用功放离线模型难以精确补偿因同频位移刚度力产生的振动[11]。

对此，本文提出基于相移陷波器的磁轴承不平衡振动全频自适应控制方法。直接以同频振动力为控制目标，将构造的轴承力输入至相移带通滤波器，该滤波器输出反馈至原控制系统电流环构成相移陷波器，其中相移陷波器为对传统陷波器的改进。通过在传统陷波器中引入相移角对定义系统灵敏度函数相位进行有效补偿，可解决传统陷波器影响系统稳定性问题。该陷波器中包含功放环节，能对功放低通特性进行自适应补偿，且无需考虑功放对同频成分影响，达到有效消除同频振动力目的，并实验验证该方法的有效性。

1含不平衡质量的磁悬浮转子系统模型

磁悬浮转子模型(文献[8])见图 1。设转子中心面为Π，径向磁轴承电磁铁A、B中心面分别为Π1、Π2。A、B的定子中心间连线与Π交于N，转子几何轴与Π、Π1、Π2分别交于O、O1、O2，转子惯性主轴与Π、Π1、Π2分别交于C、C1、C2。在Π内，以N为原点建立惯性坐标系NXY，以O为原点建立以转子自转角速度Ω转动的旋转坐标系Oεη，见图 2。

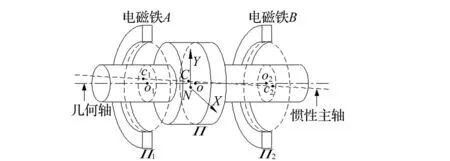
图1　磁悬浮转子示意图 Fig.1 The diagram of magnetically suspended rotor

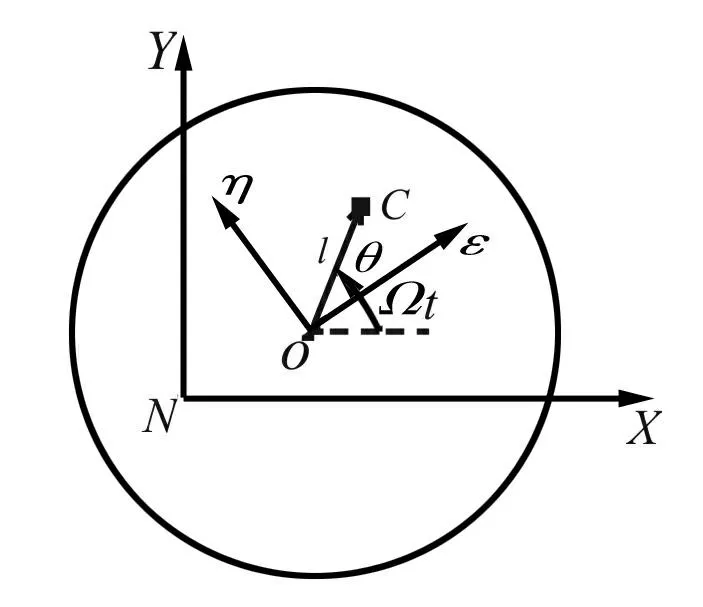
图2　坐标系示意图 Fig.2 The coordinate diagram

设OC、O1C1、O2C2长度分别为l、m、n，OC与Oε坐标轴夹角为，O1C1、O2C2在Π上投影与Oε坐标轴夹角分别为α、β，O1、O2、C1、C2在Π上投影在坐标系NXY中的坐标分别为(XA,YA)、(XB,YB)、(xA,yA)、(xB,yB)，则有

(1)

(2)

以AX通道为例，径向磁轴承力FAX在平衡点附近的线性化方程为

FAX=Kh(xAX+ΘAX)+KiiAX[xAX+ΘAX]

(3)

式中：FAX为AX通道径向轴承力；iAX[xAX+ΘAX]为磁轴承电流；Kh为位移刚度；Ki为电流刚度。

单通道磁轴承控制系统见图3。该系统由控制器、功放、电磁铁-转子组成，传递函数分别为Gc(s)、Gw(s)、P(s)。将不平衡质量等效为施加于转子位移信号中的同频扰动信号d(t)，其拉普拉斯变换为d(s)。

图3　磁轴承控制系统框图 Fig.3 The block diagram of magnetic bearing control system

2全频自适应主动振动控制方法

F(s)=-Kii(s)+KhX(s)=

-KiC(s)[X(s)-Θ(s)]+Kh[X(s)-Θ(s)]

(4)

图4　位移刚度力补偿原理图 Fig.4 The block diagram of displacement stiffness force compensation

2.1基于相移陷波器的磁轴承不平衡振动自适应控制原理

图5　基于相移陷波器的 磁轴承不平衡振动抑制原理图 Fig.5 The block diagram of suppressing unbalance vibration for magnetic bearing based on phase-shift notch filter

为有效解决功放低通特性及传统陷波器的稳定性，提出基于相移陷波器的磁轴承不平衡振全频自适应控制方法。据式(3)，实现对同频力的抑制需消除电流同频刚度力Kii[ΘAX]及位移同频刚度力KhΘAX。通常位移、电流刚度为已知量。本文直接以同频轴承力为控制目标，将构造的轴承力F(s)输入相移带通滤波器Nf(s)，输出Kii[ΘAX]+KhΘAX反馈至原控制系统的电流环构成相移陷波器N(s)，见图 5，其等效原理见图 6。其中，相移陷波器N(s)为在传统陷波器基础上引入相移角，其传递函数为

(5)

据式(5)得同频量Kii[ΘAX]+KhΘAX经陷波器N(s)后获得有效抑制，达到消除同频振动力目的。由于陷波器N(s)中含功放，对功放低通特性进行自适应补偿，故该过程无需考虑功放对同频成分影响。以不平衡量d(s)为输入、轴承力F(s)为输出，传递函数为

(6)

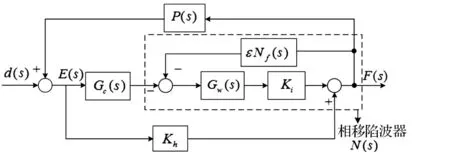
图6　磁轴承不平衡振动抑制等效原理图 Fig.6 The equivalent block diagram of suppressing unbalance vibration

2.2全频稳定性分析

据式(6)得系统闭环特征方程为

1+KiGc(s)Gw(s)P(s)-KhP(s)+

εKiNf(s)Gw(s)=0

(7)

式(7)可转化为

(8)

定义灵敏度函数为

(9)

在原系统稳定前提下，S(s)极点均位于左半平面。式(8)可简化为

s2+Ω2+ε(scosθ-Ωsinθ)S(s)=0

(10)

由式(10)知，ε=0时存在s=±jΩ。将ε作为自变量、s为应变量，ε→0时对ε求导可得在s=±jΩ附近s随ε的变化趋势，即

(11)

满足式(11)可保证闭环特征根在左半平面。其中，arg[·]为幅角。式(10)两边对ε求导得

(12)

由式(11)、(12)知，使系统稳定，须满足

-90°

(13)

对灵敏度函数S(s)，理论上相位在整个有效频率范围内从270°变化到-90°，见图 7，可见无法满足全频稳定要求。不同转速下通过θ不同取值对灵敏度函数S(s)相位进行自适应补偿，使其满足式(13)。θ随转速自适应调节表达式为

(14)

当Ω1，Ω2满足式(15)时，式(13)成立，系统在整个有效频率范围内是稳定的。

(15)

图7　灵敏度函数相频特性曲线图 Fig.7 Phase-frequency diagram of the sensitivity function

设存在f1，f2，f3使arg[S(jf1)]=180°，arg[S(jf2)]=90°，arg[S(jf3)]=0°，实现整个转速范围内的系统稳定。由式(15)得

(16)

对磁悬浮刚性转子，运行转速远小于一阶模态，因此高频特性的未建模动态不予考虑。实际模型St(s)与理论模型S(s)关系可表示为

St(s)=S(s)[1+Δ(s)]

(17)

(18)

(19)

式中：k1=(lgf2-lgf1)/90；k2=(lgf3-lgf2)/90。

(20)

式(16)转化为

(21)

由(21)知，Ω1，Ω2的取值范围变小，为保证一定稳定裕度，取

(22)

系统仿真参数见表 1。据表1参数及对f1，f2，f3的定义，得f1=8.48 Hz，f2=70 Hz，f3=118 Hz。研究对象灵敏度函数不确定性可设为ρ=0.2，得Ω1=2138 r/min，Ω2=5432 r/min。据式(14)、(16)，转速为0～2138r/min时陷波器相移θ=-180°；转速为2138～5432r/min时θ=-90°；转速为5432～8000 r/min时θ=0°。ε=1，θ不同取值时关于Ω2的主导根轨迹见图8。由图8知，θ=-180°、转速为0～2138 r/min时系统稳定；θ=-90°、转速为2138～5432 r/min时稳定；θ=0°、转速为5432～ 8000 r/min时稳定，满足转子整个转速范围的稳定。而ε不影响虚轴穿越点，即不影响临界稳定转速。

表1　仿真参数

图8　闭环系统主导根轨迹图 Fig.8 Dominant root locus of the closed-loop system

3实验验证

利用北京航空航天大学研制的磁悬浮控制力矩陀螺样机进行实验验证，见图 9。磁悬浮转子系统用DSP+FPGA控制系统，系统采样频率为6.67 kHz。

为验证本文方法实现全转速范围内不平衡振动控制的有效性，在三个转速阶段分别以1200 r/min、3600 r/min、6600 r/min进行实验。位移及电流信号以电压形式输出，通过示波器采集，实验结果见图10。由于所用实验装置无轴承力传感器，轴承力由采集的位移、电流按式(3)相加等效而成。图10(a)轴承力幅值由1.2 N减少到0.25 N，减少79.2%；图10(b)轴承力幅值由0.75 N减少到0.15 N，减少80%。由图10(a)、(b)看出，轴承力并非完全收敛于零。因实际系统中传感器检测面不均匀及磁轴承非线性等使轴承力含倍频成分。由图10(c)看出，高速时轴承力幅值本身较小，加入相移陷波器后有一定衰减，但衰减不明显，因此时同频轴承力已非幅值最大振动力。实验结果证明该方法能在整个转速范围内有效减少同频轴承力，其有效性获得验证。

图9　磁悬浮控制力矩陀螺样机 Fig.9 The experimental setup of magnetically suspended control moment gyro

(a) θ=-180°,转速1200r/min(b) θ=-90°,转速3600r/min(c) θ=0°,转速6600r/min图10 转子位移、电流及轴承力响应图Fig.10Transientresponseofdisplacement,currentandmagneticbearingforce

4结论

(1)引入相移带通滤波器构成相移陷波器，据转速自适应补偿灵敏度函数相位，实现整个转速范围内消除振动力。且通过设置三个不同相移值能保证一定的稳定裕度。

(2)与在零同频电流基础上加同频位移刚度力补偿方法相比，本文方法自适应补偿功放的低通特性，无需考虑功放对补偿效果影响，可简化设计过程。

(3)利用该方法能消除同频轴承力，但高速情况下效果不明显。对其它频率成分振动力的有效抑制尚待研究。

参考文献

[1]郑世强,房建成,魏彤,等. MSCMG磁轴承μ综合控制方法与实验研究[J]. 仪器仪表学报,2010, 31(6): 1375-1380.

ZHENG Shi-qiang, FANG Jian-cheng, WEI Tong, et al. Experimental study on μ synthesis control for magnetic bearings of MSCM G[J]. Chinese Journal of Scientific Instrumen, 2010, 31(6): 1375-1380.

[2]Abdelfatah M M, Ilene B V. Imbalance compensation and automation balancing in magnetic bearing systems using the Q-parameterization theory[J]. IEEE Transactions on Control Systems Technology, 1995, 3(2): 202-210.

[3]Fang J C, Ren Y. Decoupling control of a magnetically suspended rotor system in control moment gyros based on an inverse system method[J]. IEEE/ASME Transactions on mechatronic, 2010, 17(6): 1133-1144.

[4]冯锐,郑世强,房建成. 高速磁悬浮电动机对拖实验中转子不平衡质量在线辨识与振动控制[J]. 机械工程学报, 2014, 50(3): 71-77.

FENG Rui, ZHENG Shi-qiang, FANG Jian-cheng. Online identification and unbalanced vibration control of high-speed magnetically levitated motor for drag test[J]. Journal of Mechanical Engineering, 2014, 50(3): 71-77.

[5]龙亚文,谢振宇,徐欣. 磁悬浮轴承H鲁棒控制策略研究[J]. 振动与冲击,2013,32(23):115-120.

LONG Ya-wen, XIE Zhen-yu, XU Xin. H robust control strategy for an active magnetic bearing[J]. Journal of Vibration and Shock,2013,23(23):115-120.

[6]Lum K W, Coppla V T, Bernstein D S. Adaptive autocentering control for an active magnetic bearing supporting a rotor with unkown mass imbalance[J]. IEEE Transactions on Control Systems Technology, 1996, 4(5): 587-597.

[7]Shi J, Zmood R, Qin L J. The direct method for adaptive feed-forward vibration control of magnetic bearing systems[C]. Seventh International Conference on Control, Automation, Robotics and Vision, Singapore, 2002.

[8]Bi C, Wu D Z, Jiang Q , et al. Automatic learning control for unbalance compensation in active magnetic bearings[J]. IEEE Transactions on Magnetics, 2005, 41(7): 2270-2280.

[9]刘彬,房建成,刘刚,等. 磁悬浮飞轮不平衡振动控制方法与实验研究[J]. 机械工程学报,2010, 46(12): 188-194.

LIU Bin, FANG Jian-cheng, LIU Gang, et al. Unbalance vibration control and experiment research of magnetically suspended flywheels[J]. Journal of Mechanical Engineering, 2010, 46(12): 188-194.

[10]魏彤,向岷. 磁悬浮高速转子基于位移刚度力超前前馈补偿的高精度自动平衡方法[J]. 机械工程学报，2012,48(16):184-191.

WEI Tong, XIANG Min.Autobalancing for magnetically suspended high-speed rotors based on lead feedforward compensation for displacement stiffness force[J]. Journal of Mechanical Engineering, 2012, 48(16): 184-191.

[11]Fang J C, Xu X B, Tang J Q, et al. Adaptive complete suppression of imbalance vibration in AMB systems using gain phase modifier[J]. Journal of Sound and Vibration, 2013, 332(24): 6203-6215.