多股簧系统动态响应等效线性化分析
2016-01-15赵昱,王时龙,周杰等
第一作者赵昱男,博士生,1988年12月生
通信作者王时龙男,博士,教授,1966年8月生
多股簧系统动态响应等效线性化分析
赵昱1,2,王时龙1,2,周杰1,2,孙守利1,2,李川3
(1.重庆大学机械传动国家重点实验室,重庆400044;2.重庆大学机械工程学院,重庆400044;3. 重庆工商大学检测控制集成系统重庆巿工程实验室,重庆400044)
摘要:分析归一化Bouc-Wen模型描述的滞迟阻尼能量损耗,建立该模型极限环在任意变形幅值下能量损耗计算公式及快速计算方法,提出多股簧系统频率响应特性的等效线性化分析方法并用数值仿真进行验证。结果表明,等效线性化分析与数值仿真结果一致,且计算速度远高于数值仿真。该方法可显著提高多股簧系统设计效率,对工程中大量具有近似线性系统响应特性的多股簧系统设计有实际意义。
关键词:多股簧;Bouc-Wen模型;能量损耗;等效线性化
基金项目:国家自然科学基金项目(51375508,51375517);教育部创新团队计划(IRT1196);重庆高校创新团队项目(KJTD201313)
收稿日期:2014-07-14修改稿收到日期:2014-09-25
中图分类号:TH122
文献标志码:A
DOI:10.13465/j.cnki.jvs.2015.20.009
Abstract:The energy dissipation of hysteretic damping described by the normalized Bouc-Wen model was studied. An equation for calculating the energy dissipation under arbitrary deformation amplitude was established and a fast evaluation approach was provided as well. On this basis, an equivalent linearization analysis method for the dynamic response of systems with stranded wire helical springs was proposed. Numerical simulations were carried out to verify the proposed method. The results obtained by the proposed method coincide well with those obtained by the numerical method while the proposed method is much more efficient than the numerical method. The equivalent linearization method is able to improve the efficiency of the designing of systems with stranded wire helical springs significantly; therefore, it is of practical value for the designing of many practical systems with approximate linear response characteristics.
Equivalent linearization analysis of the dynamic response of systems with stranded wire helical springs
ZHAOYu1,2,WANGShi-long1,2,ZHOUJie1,2,SUNShou-li1,2,LIChuan3(1. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China;2. College of Mechanical Engineering, Chongqing University, Chongqing 400044, China;3. Engineering Laboratory for Detection, Control and Integrated System, Chongqing Technology and Business University, Chongqing 400044, China)
Key words:stranded wire helical spring; Bouc-Wen model; energy dissipation; equivalent linearization

图1 多股簧 Fig.1 A stranded wire helical spring
多股簧为由多层多股钢丝拧制的钢丝绳卷绕而成的螺旋弹簧[1],见图1。由于减振效果优良、服役寿命长,常用于自动武器等关键部件[2]。多股簧加工、检测已实现数控及自动化[3-4],并在更多领域受到重视。
多股簧结构复杂,受载变形时弹簧内部钢丝间相互挤压并相对滑动,导致呈一定非线性刚度及滞迟阻尼,其动态响应常用一种修正的Bouc-Wen模型描述[2]。Bouc-Wen模型[5-6]用于描述磁流变装置[7]、钢丝绳减振器[8]等滞迟阻尼器件,具有显著的非线性表达式,使其响应分析较困难。Okuizumi等[9]提出的基于多尺度法分析方法只能处理特殊的Bouc-Wen模型且计算过程复杂;Wong等[10]提出的多谐波分析法涉及大量迭代计算易遇收敛问题且分析耗时较长。工程中设计多股簧系统时仍采用数值方法,该方法耗时较长,因而降低设计分析效率,不利于多股簧推广应用。
等效线性化方法作为非线性系统分析的常用方法分析速度快,且对非线性不很强系统往往能给出满足工程精度要求结果。大量观测表明,常见的多股簧系统中通常不会出现超谐波、次谐波响应、分岔等典型非线性响应现象,符合等效线性化分析应用条件。本文通过分析归一化Bouc-Wen模型的能量损耗,以单自由度系统为例研究多股簧系统等效线性化分析方法,旨为多股簧系统设计提供高效分析手段。
1多股簧系统模型
1.1多股簧恢复力-变形量模型
多股簧轴向受载变形时的恢复力与变形量之关系即为多股簧恢复力-变形量模型。多股簧在周期载荷下的恢复力-变形量关系见图2。
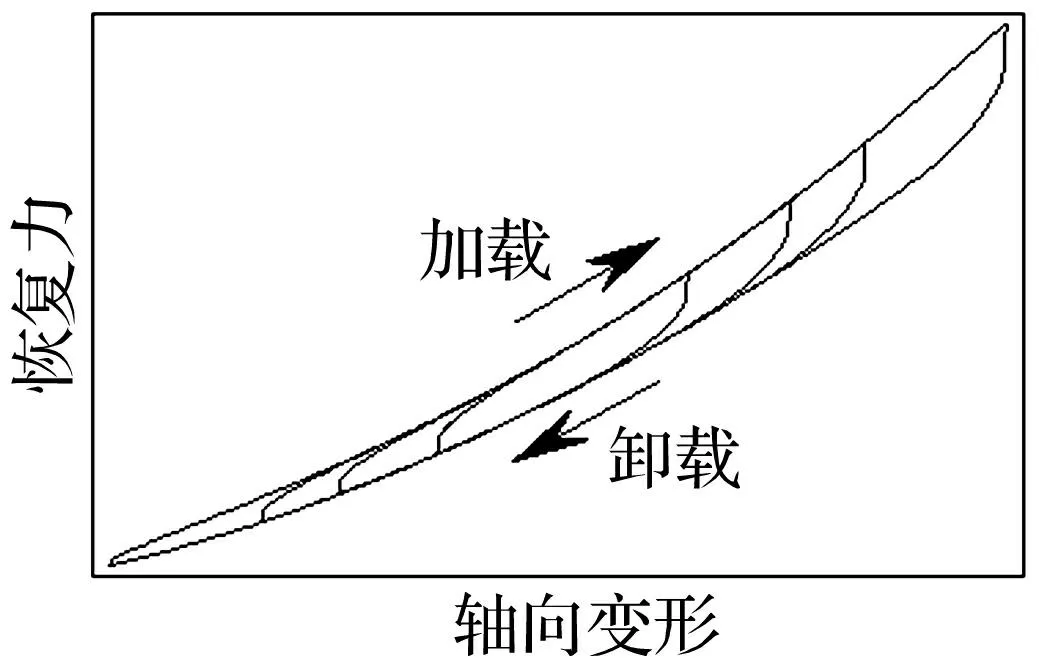
图2 典型多股簧恢复力-变形量示意图 Fig.2 Illustration of the typical restoring force-deformation relation of stranded wire helical spring
多股簧动态响应可用修正的Bouc-Wen模型描述,即
(1)
式中:“·”为对时间t求导;r为总恢复力;-1<ω<1为由归一化Bouc-Wen模型描述的滞迟力;Δ为多股簧变形量;t为时间;kEi为刚度系数;kAi为滞迟阻尼放大系数;N,M为多项式阶数;σ>1/2,ρ>0,κω>0,n>0均为归一化Bouc-Wen模型参数。该诸参数均可通过文献[2]参数识别方法的实验数据识别获得。
1.2单自由度多股簧系统运动方程

图3 单自由度系统模型 Fig.3 Structure of the single degree of freedom system
由质量块m、单股弹簧ks、线性阻尼c0及多股簧组成的单自由度微型悬挂装置系统结构见图3。系统中单股簧用作传感器,通过测量其载荷即可求得质量块位移。令ks=0,则系统看完简化为简单多股簧悬挂系统。
图3系统中单股弹簧上端固定,多股簧下端与可周期振动基础相连,质量块与两弹簧自由端相连。其中yg为基础激励位移,y为质量块m与基础的相对位移。考虑重力及系统静止时两弹簧预压,设系统具有零初始条件y(0)=0,ω(0)=0,用式(1)建立系统运动方程为
(2)
式中:yg为幅值为Ag频率为f的简谐激励,即
yg(t)=Agsin(2πft)
(3)
为便于分析计算,需对式(2)进行无量纲化处理。引入空间尺度L、时间尺度T,定义无量纲量位移为x,无量纲时间为τ,令有、无量纲量关系为

(4)
用式(2)~式(4)得无量纲运动方程为
(5)
式中:αEi为刚度系数;αAi为滞迟阻尼放大系数;cd为阻尼系数;Ω为频率;F为激励幅值;即
(6)
αAi=L1-iT2κωkAi/m
(7)
cd=Tc0/m
(8)
Ω=2πfT
(9)
F=T2Ag(ks-Ω2m)/(Lm)
(10)
2归一化Bouc-Wen模型的能量损耗分析
文献[11]基于高斯超几何函数研究Bouc-Wen模型解析解。用高斯超几何函数可建立归一化Bouc-Wen模型极限环变形幅值与能量损耗关系,为等效线性化分析基础。
2.1归一化Bouc-Wen模型极限环
式(5)归一化Bouc-Wen模型参数满足σ>1/2时其极限环的有界输入、输出(BIBO)稳定,且输出z的极限为±1[12]。x取不同幅值时生成的2个极限环ABCD见图4。极限环A、C点为x达到极值点,B、D点为z=0点。虚线AECF为以A、C为对角顶点的假想矩形。
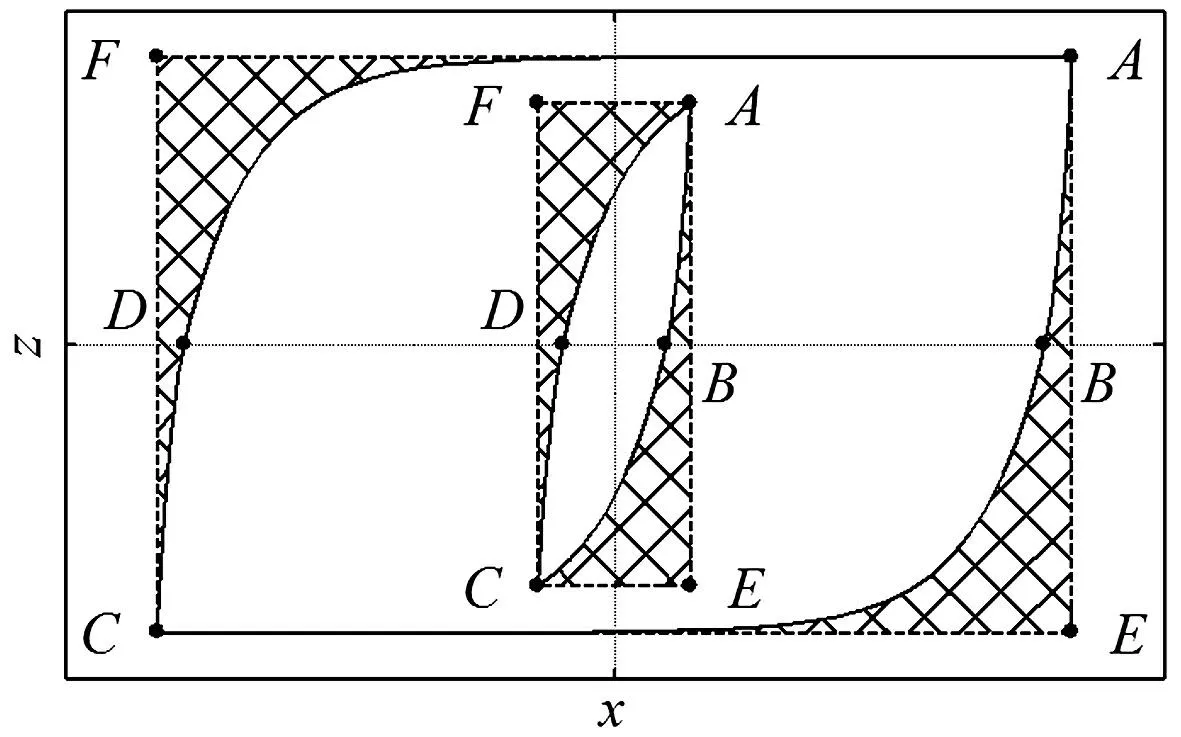
图4 归一化Bouc-Wen模型极限环 Fig.4 Limit cycles of the normalized Bouc-Wen model
式(5)无量纲归一化Bouc-Wen模型可写为
(11)
x′、z同号时由式(11)可得AD、BC段解析式,即
(12)
x′、z异号时可得CD、AB段解析式,即
(13)
式中:2F1为高斯超几何函数[13];C1,C2为待定常数。
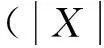
(14)
利用Bouc-Wen模型对称性得D点横坐标xD为
(15)
以曲线AD为分析对象,由式(12)中对应曲线AD的常数C1为
C1=xD
(16)
(17)
将式(15)、(16)代入式(17)并化简,得
(18)
式中:β为不完全函数。
2.2归一化Bouc-Wen模型能量损耗
归一化Bouc-Wen模型一个周期内的能量损耗E即为图4中极限环所围面积,计算式为
E=2(SADx-SABx)
(19)
式中:SADx为曲线AD与x轴所围面积;SABx为曲线AB与x轴所围阴影面积,即
(20)
据式(11),将式(20)改写为
(21)
利用超几何函数写出式(21)中积分解析式为
(22)
同理可得SADx为
(23)
将式(22)、(23)代入式(19)求得
(24)
2.3能量损耗快速计算
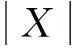
E=ET+4(X-XT)
(25)
为进一步加快等效线性化分析速度,可在[0,XT]区间内均匀产生一系列X值,利用并行算法求出其对应的E并保存为数据表,分析中需要计算某X值对应的E值时即可利用插值法快速得到结果。
取Bouc-Wen模型参数为σ=2、ρ=1、n=1/2,利用本方法及数值仿真所得E-X曲线见图5。仿真时先通过Runge-Kutta法由式(5)得到极限环,再用“鞋带公式”[14]计算极限环面积。由图5可知,本文方法分析结果与数值仿真结果吻合较好。
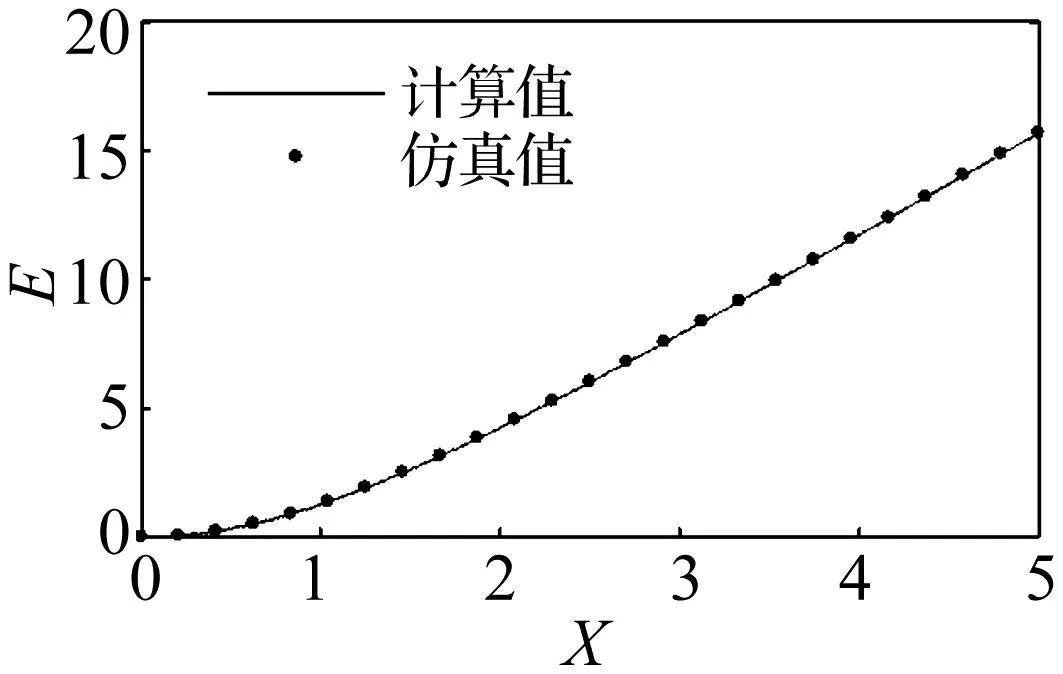
图5 归一化Bouc-Wen模型能量损耗 Fig.5 Energy dissipation of the normalized Bouc-Wen model
3系统频率响应特性等效线性化分析
等效线性化分析为用简单线性系统近似描述复杂的非线性系统。设式(5)的等效线性化形式为
x″+(cd+ce)x′+kex+Fsin(Ωτ)=0
(26)
式中:“′”为对无量纲时间τ求导;ke为等效刚度系数;ce为多股簧滞迟阻尼等效阻尼系数。
由式(2)知,多股簧刚度特性由其变形量即y的多项式表示。因此,质量块在原点附近小幅振动时可将非线性刚度用其一阶近似值代替。系统受零均值简谐激励时等效线性系统响应亦为零均值。取多股簧响应模型中非线性弹性项一次项系数作为等效刚度,即
ke=αE1
(27)
同理,多股簧恢复力-变形量模型式(5)中滞迟阻尼非线性放大多项式在小振幅时亦可用一阶形式近似
(28)
此时,归一化Bouc-Wen模型极限环被一次函数调制,形状见图6。
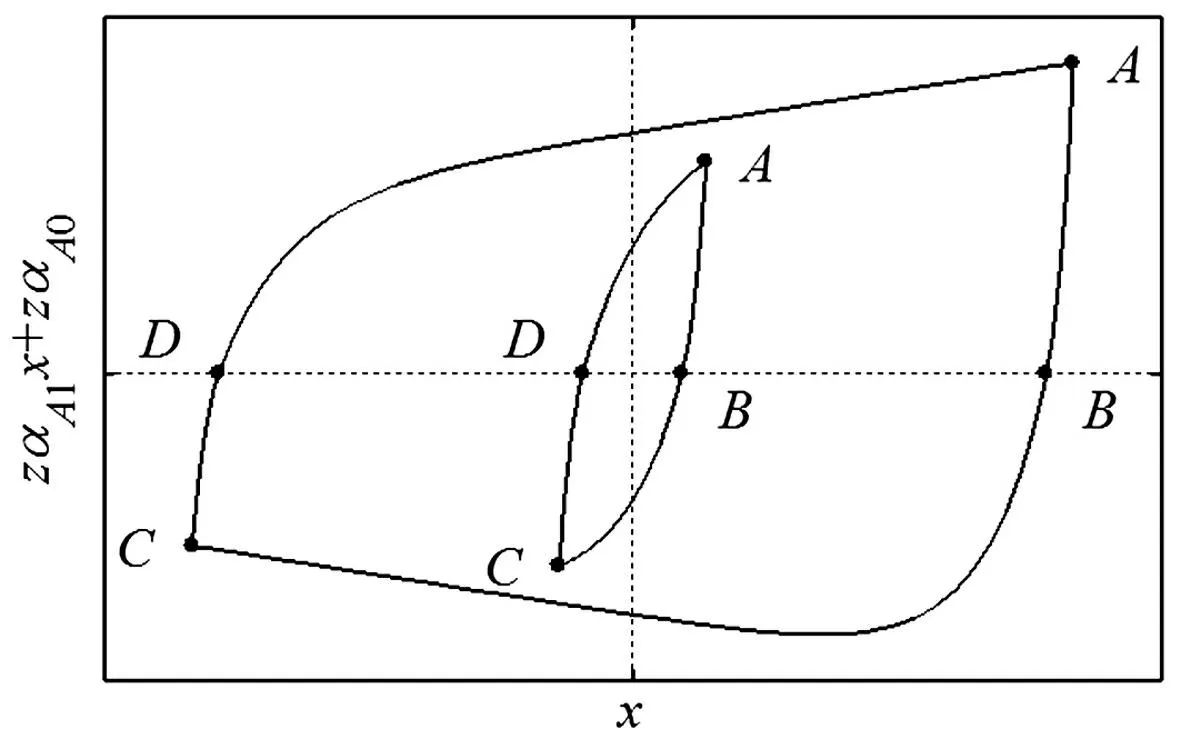
图6 经调制的极限环 Fig.6 Modulated limit cycles
由于归一化Bouc-Wen模型产生的极限环对称,经一次函数调制后极限环面积不会改变,因此调制后极限环消耗能量Es为
Es=αA0E
(29)
等效阻尼系数ce的取值应使等效线性化系统能量消耗即等效阻尼力做功Es与滞迟阻尼消耗能量Ec相等。等效线性系统在简谐激励下的稳态相对位移表达式为
x=Xsin(Ωτ-φ)
(30)
式中:Ω为激励圆频率;φ为响应与激励相位差。
阻尼力Fc为
Fc=ceXΩcos(Ωτ-φ)
(31)
阻尼力做功即系统能量损耗Ec为
(32)
系统等效阻尼系数ce可表示为
(33)
式(26)等效线性系统稳态响应幅频特性为
(34)
相频特性为
(35)
联立式(18)、(24)(或(25))、(34)可得关于X、E的代数方程组。利用Levenberg-Marqardt等非线性方程数值求解算法[15]可方便求出X、E数值。
工程中一般更关心绝对位移幅频特性,只需将激励与相对位移响应合成即可。据式(3)、(4)、(30)可写出稳态响应的绝对位移xa为
xa=XΩsin(Ωτ-φ)+(Agsin(Ωτ))/L
(36)
其振幅Xa为
(37)
由分析过程知,等效线性化分析方法将复杂非线性微分方程求解转化成简单的代数方程求解,无需时程分析即可求出系统的频响特性,因而可提高分析效率;但等效线性化分析中的能量损耗及振幅计算等过程始终针对稳态响应进行。因此,该方法只适用系统的频响特性分析,不适用过渡状态或时程分析。
4仿真验证
数值仿真为检验等效线性化分析有效性途径。用数值仿真求系统幅频特性过程为:①用Runge-Kutta法求系统在某一激励频率下若干周期的时程响应;②求出最后一个周期的响应振幅及均值,记录系统最终状态;③以最终状态作为初始状态再求若干周期的时程响应;④计算最后一个周期的响应振幅及均值,记录系统最终状态;⑤计算第2、4步记录的振幅及均值间相对误差,若误差小于要求值则改变激励频率,重复①~⑤;若误差大于要求值则重复③~⑤。本文数值仿真及等效线性化分析程序均用Mathematica编写。
取系统参数m=15 kg,ks=5 000 N/m,c0=50 Ns/m,kE2=105N/m2,kE1=5 000 N/m2,kA1=40/m,kA0=1/m,κω=7 N,n=0.5,σ=2,ρ=1 000。频率范围1~15 Hz,在此范围内共分析40个频率点的系统响应。
分别用等效线性化及数值仿真法分析系统响应,所得系统在激励幅值Ag为2 mm、4 mm、6 mm时相对位移幅频特性见图7。由图7可知,相对位移随激励频率增加先逐渐减小在一定频率下相对位移接近0后,响应振幅逐渐增大到共振,共振后又逐渐减小并趋于与激励振幅相同。

图7 相对位移幅频特性 Fig.7 Magnitude response of the relative displacement

图8 相对位移相频特性 Fig.8 Phase response of the relative displacement
利用等效线性化方法直接可获得系统相频特性。Ag=4 mm时相对位移相频特性见图8。其它激励幅值下相频特性与图8类似。由图8可知,等效线性系统的相频特性与一般线性系统类似,响应相位差随频率增加而增加,共振时相位差达90°;激励频率很高时相位差接近180°,此时绝对位移接近0。
工程中更关心系统的绝对位移响应。在激励幅值Ag为不同值时的绝对位移幅频特性见图9。由图9可知,等效线性化与数值仿真分析结果一致。激励幅值较小时等效线性化分析振幅偏小,随激励振幅增加误差逐渐减小;激励振幅继续增加时等效线性化振幅较数值仿真结果大,误差逐渐增加。因振幅增大后多股簧恢复力-变形量模型中非线性因素影响逐渐增大,使等效线性系统对非线性系统近似精度降低。
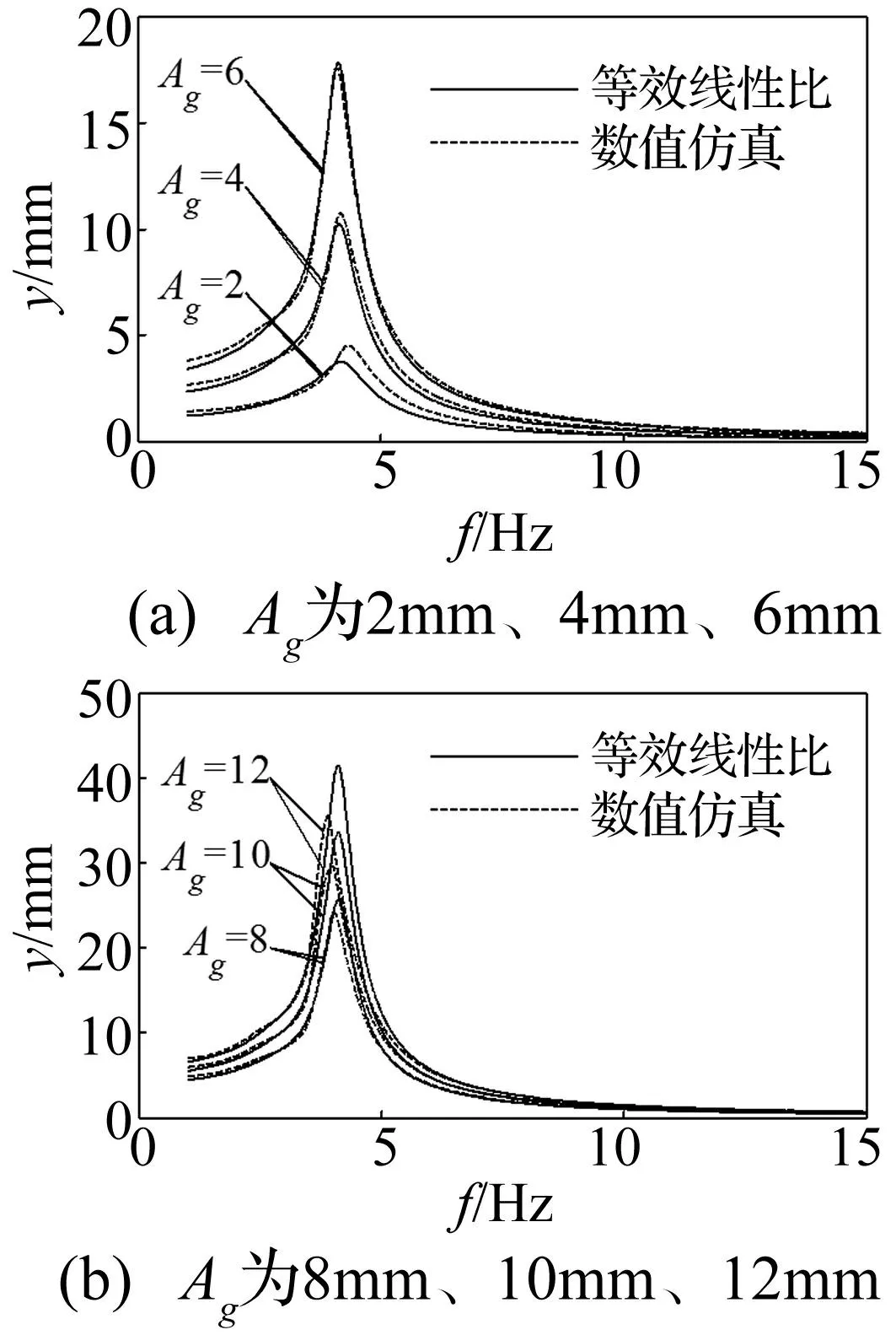
图9 绝对位移幅频特性 Fig.9 Magnitude response of the absolute displacement
等效线性化分析的最大优势为计算耗时少效率高。数值仿真与等效线性化分析耗时对比见表1。由表1可见,等效线性化耗时远小于数值仿真,由此表明,等效线性化分析为能显著提高分析效率方法。实际工程中设计含多股簧系统时可将其作为初步设计分析方法,设计系统各参数大致值,再利用数值仿真等校核,进一步优化设计参数,提高设计效率。

表1 分析时间
5结论
在研究归一化Bouc-Wen模型能量损耗基础上提出多股簧系统等效线性化分析方法,结论如下:
(1)归一化Bouc-Wen模型极限环在任意变形幅值下的能量损耗可通过高斯超几何函数精确表达,并可由求解关于输出幅值及能量损耗的代数方程求出。等效线性化分析前可利用并行计算快速建立能量损耗数据表,分析过程中利用插值法可快速获得特定振幅下的能量损耗。
(2)等效线性化分析能避免非线性微分方程求解,而通过代数方程求解系统的频率响应特性,显著提高分析效率。
(3)等效线性化分析误差与激励幅值有关,在一定范围内误差先随激励幅值增加而减小,而后随激励振幅增加而增大。
(4)等效线性化方法适用分析工程中大量具有近似线性系统响应特性的多股簧系统频率响应特性,不适用系统时程分析。
参考文献
[1]王时龙,雷松,周杰,等. 两端并圈多股弹簧的冲击响应研究[J]. 振动与冲击,2011,30(3):64-68.
WANG Shi-long,LEI Song,ZHOU Jie,et al. Impact response of stranded wires helical springs with closed ends[J]. Journal of Vibration and Shock,2011,30(3):64-68.
[2]Zhao Y,Wang S L,Zhou J,et al. Modeling and identification of the dynamic behavior of stranded wire helical springs[J]. Journal of Vibroengineering,2013, 15(1): 326-339.
[3]Peng Y X,Wang S L,Zhou J,et al. Structural design, numerical simulation and control system of a machine tool for stranded wire helical springs[J]. Journal of Manufacturing Systems, 2012, 31(1SI): 34-41.
[4]王时龙,张明明,周杰,等. 振动状态下螺旋弹簧运动状态模型[J]. 机械工程学报,2012,48(1):78-83.
WANG Shi-long,ZHANG Ming-ming,ZHOU Jie,et al. Motion model of helical springs under vibrational condition[J]. Journal of Mechanical Engineering,2012,48(1):78-83.
[5]Bouc R. Forced vibration of mechanical systems with hysteresis[C]// Djadkov S. Proceedings of the 4th Conference on Nonlinear Oscillations. Prague:Academia,1967: 315.
[6]Wen Y K. Method for random vibration of hysteretic systems[J]. Journal of the Engineering Mechanics Division, 1976, 102(2): 249-263.
[7]相恒波,方秦,王玮,等. 磁流变阻尼器抗爆隔震性能的数值模拟[J]. 振动与冲击,2007,26(11):106-111.
XIANG Heng-bo,FANG Qin,WANG Wei,et al. Numerical simulation on shock isolation of blast-resistant structure with magnetorheological dampers[J]. Journal of Vibration and Shock,2007,26(11):106-111.
[8]Ni Y Q,Ko J M,Wong C W,et al. Modelling and identification of a wire-cable vibration isolator via a cyclic loading test part 1: experiments and model development[J]. Proceedings of the Institution of Mechanical Engineers Part I-Journal of Systems and Control Engineering,1999, 213(I3): 163-171.
[9]Okuizumi N,Kimura K. Multiple time scale analysis of hysteretic systems subjected to harmonic excitation[J]. Journal of Sound and Vibration,2004, 272(3): 675-701.
[10]Wong C W,Ni Y Q,Lau S L. Steady-state oscillation of hysteretic differential model 1. response analysis[J]. Journal of Engineering Mechanics-Asce,1994, 120(11): 2271-2298.
[11]Charalampakis A E,Koumousis V K. On the response and dissipated energy of Bouc-Wen hysteretic model[J]. Journal of Sound and Vibration. 2008, 309(3/4/5): 887-895.
[12]Ikhouane F, Manosa V, Rodellar J. Dynamic properties of the hysteretic Bouc-Wen model[J]. Systems & Control Letters, 2007, 56(3): 197-205.
[13]Olver F W. NIST handbook of mathematical functions[M]. Cambridge: Cambridge University Press, 2010:318.
[14]Braden B. The surveyor’s area formula[J]. The College Mathematics Journal,1986, 17(4): 326-337.
[15]Burden R L,Faires J D. Numerical analysis[M]. Boston: Cengage Learning, 2010.

