一种新的多传感器群内目标精细跟踪算法

(海军航空工程学院信息融合研究所,山东烟台264001)

0 引言

在现实环境中,经常因为不可控制或特定人为目的等因素,会在一个较小的空域分布范围内构成一个复杂的目标群,如空间碎片的分裂、弹道导弹突防过程中伴随的大量碎片及诱饵、掠海飞行的导弹和飞机群等,这些目标空域分布范围较小,运动特征差异不明显,相对运动速度较低且特性接近。目标跟踪领域将此类目标称为群目标[1-5]。

在一些实际应用中,与群的整体态势相比,往往更关心群内个体目标的情况[3-4]。例如,航天器在轨爆炸后所产生的空间碎片会形成一个群目标,这个群目标将会严重威胁太空安全,为消除太空安全隐患,必须精确掌握每一个碎片的运动轨迹,简单跟踪群整体已无法满足工程实际需求;再如,当面对敌方群飞机突防时,为更好地进行战术拦截和打击,要求在探测系统只能部分分辨飞机群的条件下,尽可能精确地估计出群中飞机的个数及各架飞机的运动轨迹,以便为后续的作战决策提供精确的信息支持。此时,为改善跟踪效果,工程上通常利用多套不同的设备、从不同测向获取群目标测量数据,进行数据互联和融合等处理,多传感器探测下群内目标的精细跟踪成为必须解决的问题。

但传统的多目标跟踪算法[6-15]难以有效跟踪非机动群内目标,因为与传统多目标相比,杂波环境下群内目标的回波特性明显复杂,传统跟踪算法对群目标回波复杂性考虑不足,漏跟、错跟、多跟现象严重。此外,现有群目标跟踪算法[16-24]大多基于群整体进行跟踪,未考虑群内目标的精细跟踪问题;而小部分考虑群内目标航迹维持的算法跟踪环境又相对单一,难以工程应用。

因此,为解决该问题,本文深入分析群内目标回波特性,提出了一种基于形状方位描述符[25]的集中式多传感器群内目标精细跟踪(Centralized Multi-Sensor Refined Tracking within Group Targets Based on Shape and Azimuth Descriptor,CMSRT-GT-SAD)算法,并建立了多种典型的仿真环境,验证了本文算法的有效性。

1 系统描述

集中式多传感器群内目标跟踪问题是在杂波中用NS个传感器上报到融合中心的量测实现群内每个目标的状态更新。设系统的动态方程为

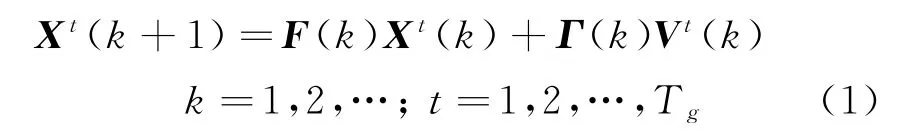
式中:X t(k+1)∈R n为k+1时刻目标的全局状态向量;F(k)∈R n为状态转移矩阵;T g为第g个群中的目标个数;Γ(k)∈R n,h为噪声分布矩阵;V t(k)为离散时间白噪声序列,且E[V t(k)]=0,E[V t(k)V t(k)T]=Q t(k)。

并假定各传感器间的量测误差是统计独立的。

2 CMSRT-GT-SAD算法

2.1 群目标形状矢量的建立

由群目标的定义可知,在非机动模式下相邻时刻群内目标真实回波构成的图形相似。基于这一原理,可以利用形状方位描述符[25]分别表示出群内各目标状态更新值和可能关联量测构成的图形。

形状方位描述符是数字图像处理中描述空间图形的一种常用方法,由图像方位框的高度、宽度、面积、比率,以及图像约束框的高度、宽度、面积、比率、最大半径、最小半径、最小半径角、最大半径角共12个分量组成[25]。

假设G t(k-1)为k-1时刻第t个群目标,群中包含4个目标,图1中的图形A为G t(k-1)的形状示意图,t1,t2,t3,t4为群内各目标的位置。则利用形状描述符建立A的形状矢量为

式中:ω1为图像方位框的高度,图像方位框为沿图像行动方向围绕物体的最小矩阵,如图2中的矩形B所示;ω2为B的宽度;ω3为B的面积;ω4为B的比率,即B的面积与A的面积之比;ω5为图像约束框的高度,图像约束框为沿图像主轴方位的包围物体最小的矩形,如图3中的矩形C所示;ω6为C的宽度;ω7为C的面积;ω8为C的比率,即C的面积与A的面积之比;ω9为最小半径,即A的重心与A的边界元素之间的最小距离;ω10为最大半径,即A的重心与A的边界元素之间的最大距离;ω11为最小半径角,即最小半径向量相对于水平轴线的角度;ω12为最大半径角,即最大半径向量相对于水平轴线的角度。

需要注意的是,当处理直线等特殊图形时,Ωt(k-1)中的有些分量可能无法获取,此时可去掉这些分量。由上述描述可知,形状矢量Ωt(k-1)唯一地表示了图形A,若两个图形的图形矢量相同,则判定这两个图形一致。

在每个时刻更新群内各目标状态矢量的同时,更新各群航迹的形状矢量;记k-1时刻群航迹t的形状矢量为…,12。

图1 群目标G t(k-1)的形状示意图

图2 图像方位框示意图

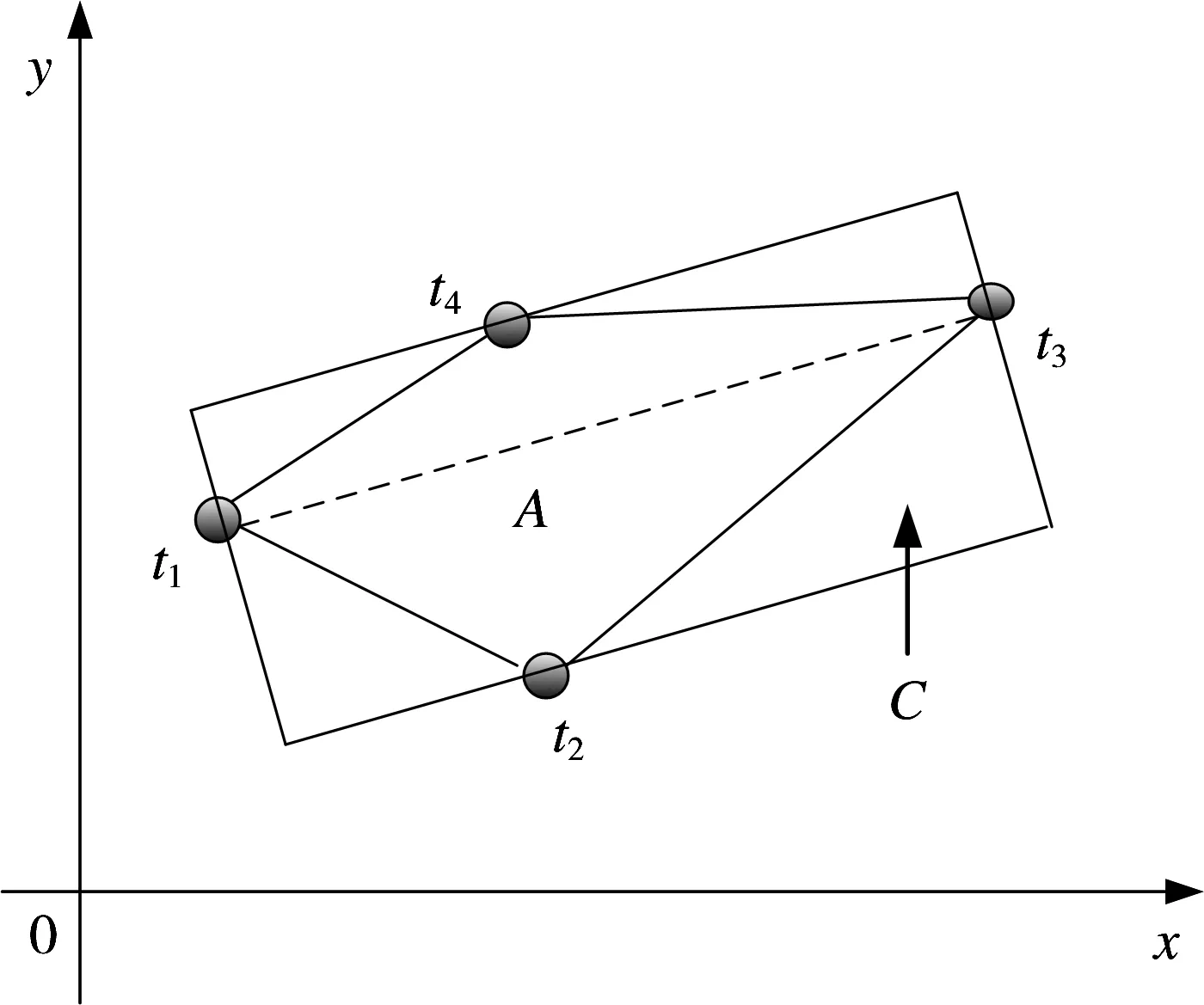
图3 图像约束框示意图

2.2 相似度模型的建立

以G t(k-1)中各目标在k时刻的一步预测值为中心建立关联波门,设Z(k)中落入关联波门的量测集为

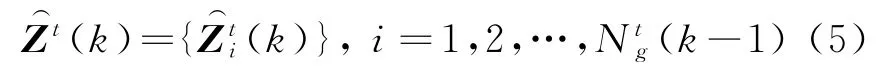
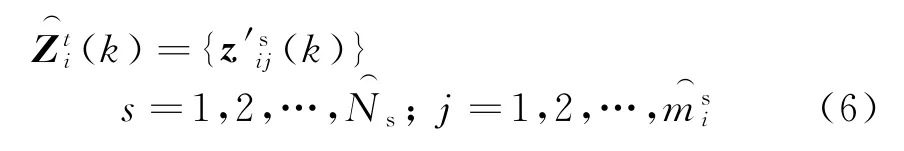
针对传感器s,基于式(7)建立矢量τ:

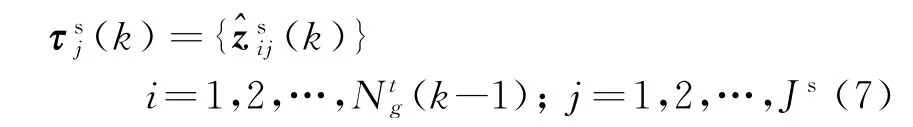
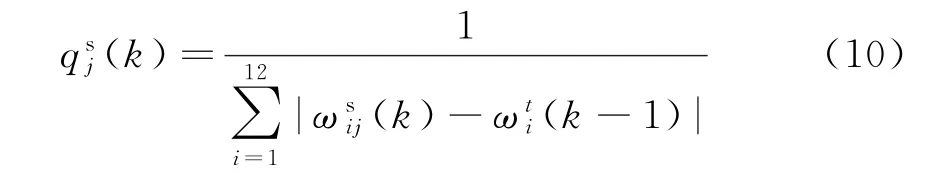
基于式(10),构建相似度集合Qs(k)=越大,说明为真的概率越大。为便于比较说明,需要进行归一化处理,在此定义ρsj(k)为

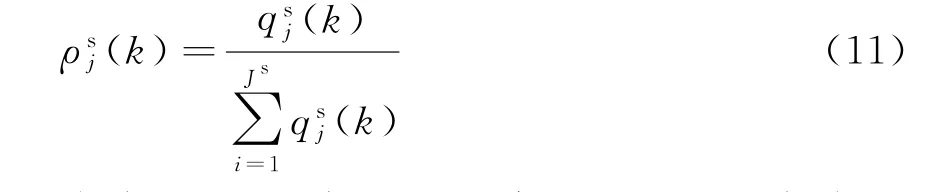
式中,

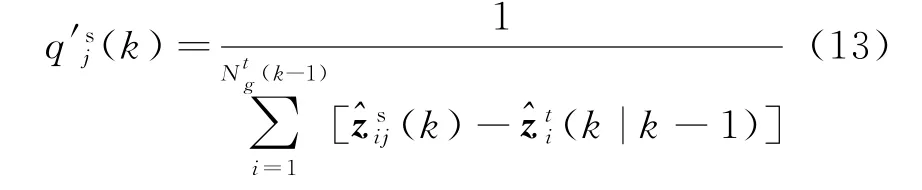
2.3 冗余图像的剔除

当利用多传感器对群目标进行探测时,可以获得对应同一群目标的多幅图像,所以需要进行冗余图像的剔除,在此基于选主站的思想解决该问题。

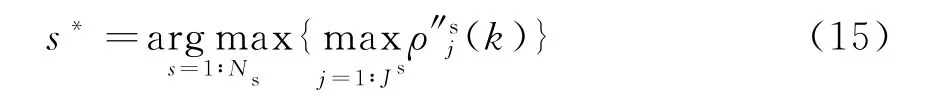
表示选择传感器s∗为主站,并利用传感器s∗上报的量测集对G t(k-1)进行状态更新。

2.4 基于粒子滤波的状态更新

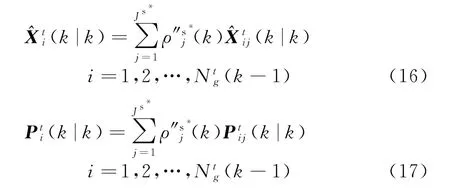
3 仿真验证与分析

为验证说明算法的性能和有效性,设定两种典型的群目标运动情况,从算法跟踪精度、实时性、有效跟踪率三个方面分析算法的跟踪性能,并与传统多传感器多目标跟踪算法中性能优越的基于数据压缩的集中式多传感器多假设(数据压缩CMS-MHT)算法[9]进行比较。

3.1 仿真环境

假定传感器为3部2D雷达,参数设置如表1所示。

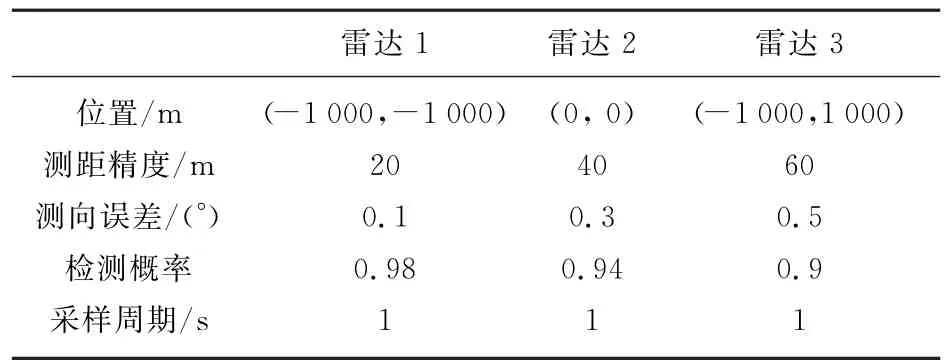
表1 传感器参数设置表

1)环境1:模拟两个交叉运动的密集群目标。设在一两维平面上存在8个目标,构成2个群,均作匀速直线运动。前4个目标组成第1个群,各目标的初始位置分别为(5 000 m,800 m),(5 200 m,1 000 m),(5 550 m,1 200 m),(5 700 m,1 400 m),初始速度均为(-200 m/s,300 m/s);第5～8个目标组成第2个群,各目标的初始位置分别为(-5 000 m,8 000 m),(-5 200 m,8 200 m),(-5 550 m,8 400 m),(-5 700 m,8 600 m),初始速度均为(100 m/s,300 m/s)。

仿真中杂波的产生分为两部分。对普通目标T0而言,以T0为中心在极坐标下建立一个边长为[10σρ,10σθ]的矩阵,在此矩阵中均匀产生λ1个杂波;对群目标G而言,计算群目标的中心点为中心在极坐标下建立一个边长为[2ΔGρ+10σρ,2ΔGθ+10σθ]的矩阵(其中ΔGρ,ΔGθ分别为G中各量测在极坐标系两坐标轴上的最大差值),在此矩阵中均匀产生λ2个杂波。在此,取λ1=2,λ2=4。

2)环境2:为验证各算法耗时和有效跟踪率随杂波的变化情况,在环境1的基础上,杂波的取值如表2所示。

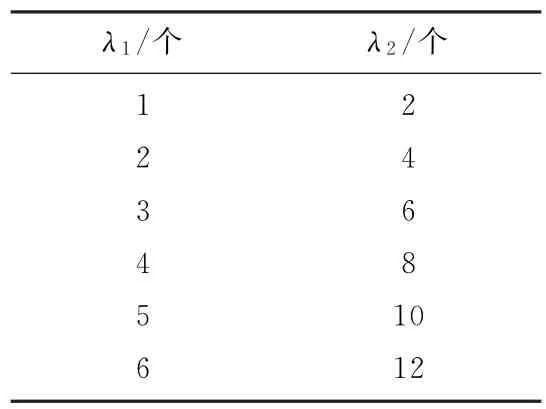
表2 环境2中杂波取值表

3.2 仿真结果及分析

图4为环境1中群目标真实态势图,从图中可以看出两个群目标交叉运动。图5和图6分别为环境1中CMSRT-GT-SAD算法和数据压缩CMS-MHT算法的均方根位置、速度误差比较图。从图中可以看出,本文算法能对目标进行有效跟踪,均方根位置误差小于60 m,均方根速度误差小于2 m/s;而数据压缩CMS-MHT算法的跟踪效果不理想,在50步以后均方根位置误差高达300 m以上,均方根速度误差高达12 m/s以上,在对跟踪精度要求较高的实际场合中已无法满足工程要求。

表3为环境2中各算法有效跟踪率及算法耗时随杂波数变化比较表。从表中可以看出,对应于同样的杂波数,CMSRT-GT-SAD算法的有效跟踪率较高,当杂波数为(6,12)时,有效跟踪率仍维持在75%以上;数据压缩CMS-MHT算法的有效跟踪率明显低于本文算法,当杂波数为(6,12)时,其有效跟踪率仅为39.34%,已不能满足工程需求。此外,随着杂波数的增加,两种算法的有效跟踪率均有所下降,但数据压缩CMS-MHT算法的下降幅度明显大于本文算法。

图4 群目标真实态势图

图5 X方向均方根位置误差比较图

图6 X方向均方根速度误差比较图

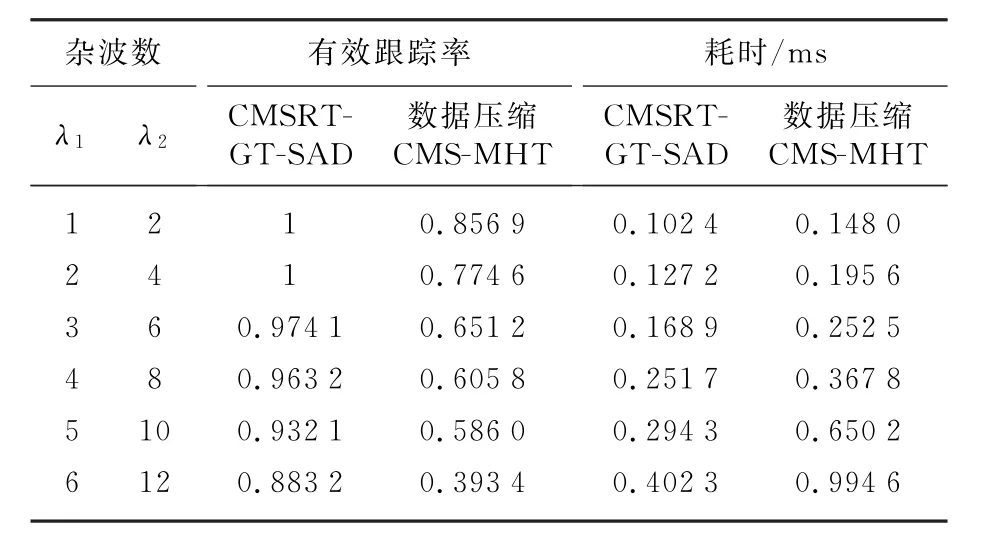
表3 各算法有效跟踪率及算法耗时随杂波数变化比较表

由表3可知,对应同样的杂波数,CMSRTGT-SAD算法的单次更新耗时小于数据压缩CMS-MHT算法。随着杂波数的增加,两种算法的单次更新耗时均有所增大;但数据压缩CMSMHT算法的增加幅度较大,当杂波数为(6,12)时,其单次更新耗时已高达0.994 6 ms,在对实时性要求较高的实际场合中已不能满足工程要求。

4 结束语

为解决多传感器群内目标的精细跟踪问题,利用相邻时刻同一非机动群内目标真实回波空间结构相对固定的特性,基于形状方位描述符,提出了CMSRT-GT-SAD算法。经仿真验证表明,该算法能较好地实现多传感器探测下非机动群内目标的精细跟踪。

但当群目标发生整体机动、分裂、合并、分散等机动时,CMSRT-GT-SAD算法将不再适用,因为各探测周期群内目标真实回波的空间结构会发生变化。多传感器探测下群内目标的机动跟踪是后续研究的重点和难点。

[1]耿文东.编队目标跟踪综述[C]∥第十届全国雷达学术年会,北京:中国电子学会,2008:367-371.

[2]邢凤勇,熊伟,王海鹏.基于聚类和Hough变换的多编队航迹起始算法[J].海军航空工程学院学报,2010,25(6):624-628.

[3]PENG Z H,SUN L,CHEN J,et al.Path Planning of Multiple UAVs Low-Altitude Penetration Based on Improved Multi-Agent Coevolutionary Algorithm[C]∥30th Chinese Control Conference,Yantai:IEEE,2011:4056-4061.

[4]QIN Zhen,SHELTON C R.Improving Multi-Target Tracking via Social Grouping[C]∥25th IEEE Conference on Computer Vision and Pattern Recognition,Providence,Rhode Island:IEEE,2012:1972-1978.

[5]赵盟盟,张群,陈怡君,等.一种用于空间群目标分辨的滑动窗轨迹跟踪算法[J].宇航学报,2015,36(10):1187-1194.

[6]何友,王国宏,关欣,等.信息融合理论及应用[M].电子工业出版社,2010.

[7]TRAN A,MANZANERA A.A Versatile Object Tracking Algorithm Combining Particle Filter and Generalised Hough Transform[C]∥International Conference on Image Processing Theory,Tools and Applications,Orleans,France:IEEE,2015:105-110.[8]ZHOU H,GAO Y,YUAN G,et al.Adaptive Multiple Cues Integration for Particle Filter Tracking[C]∥IET International Radar Conference,Hangzhou:IET,2015:1-6.

[9]张晶炜,熊伟,何友.基于数据压缩的多传感器多假设算法[J].北京航空航天大学学报,2007,33(12):1448-1451.

[10]JIN Y,DING Y,HAO K,et al.An Endocrine-Based Intelligent Distributed Cooperative Algorithm for Target Tracking in Wireless Sensor Networks[J].Soft Computing,2015,19(5):1427-1441.

[11]陈帅,郑世友,张世仓.并行多传感器多目标跟踪系统性能优化算法[J].计算机仿真,2015,32(10):69-73.

[12]陈金广,江梦茜,马丽丽,等.具有形状信息的多传感器群目标跟踪算法[J].计算机工程与应用,2015,51(17):210-216.

[13]BEARD M,REUTER S,GRANSTRÖM K,et al.Multiple Extended Target Tracking with Labeled Random Finite Sets[J].IEEE Trans on Signal Processing,2016,64(7):1638-1653.

[14]BEARD M,VO B T,VO B N.Bayesian Multi-Target Tracking with Merged Measurements Using Labelled Random Finite Sets[J].IEEE Trans on Signal Processing,2015,63(6):1433-1447.

[15]金亮亮,刘亚云.一种改进自适应机动目标跟踪算法[J].雷达科学与技术,2014,12(1):97-100.

[16]郭巳秋.粒子群优化目标跟踪方法及技术[D].北京:北京理工大学,2015.

[17]邵燕生.一种面向图像信息传输的目标跟踪算法研究[J].计算机与数字工程,2015,43(12):2155-2157.

[18]PANAKKAL V P,VELMURUGAN R.A Factor Graph Approach for Efficient JPDA Implementation in Multi-Target Tracking[C]∥IEEE Aerospace Conference,Bigsky,MT:IEEE,2015:1-15.

[19]PLOPLYS N J,KENEFIC R J.Multiple Hypothesis Tracking Using Maximum Weight Independent Set:US9291708[P].2016-03-22.

[20]KIM C,LI F,CIPTADI A,et al.Multiple Hypothesis Tracking Revisited[C]∥IEEE International Conference on Computer Vision,Santiago,Chile:IEEE,2015:4696-4704.

[21]吴晓雨,吴凌琳,杨磊.基于压缩感知的粒子滤波跟踪算法[J].系统工程与电子技术,2015,37(11):2617-2622.

[22]张明杰,康宝生.一种基于图模型的粒子滤波跟踪方法[J].计算机应用研究,2016,33(2):590-593.

[23]陈飞.多目标跟踪的边缘分布贝叶斯滤波方法研究[D].深圳:深圳大学,2015.

[24]于洪波,王国宏,曹倩.基于聚类的多目标自适应互联跟踪算法[J].中国科学:信息科学,2015,45(8):953-967.

[25]PRATT W K.数字图像处理[M].邓鲁华,张延恒,译.北京:机械工业出版社,2005.